带时间窗报童问题的供应链协调优化
陈 欢, 李 芳
(上海理工大学 管理学院,上海 200093)
报童问题模型是欧美等发达国家研究的主要管理学模型,是典型的单阶段、随机需求模型.在不确定需求的时令性商品的销售中,过量订货或不足订货都会产生损失,决策者需要确定商品的最优订购数量,使得利润最大化.由于服务业产品多数具备报童模型中的商品特征,随着服务产业的发展,对于报童问题模型的研究越显重要.
报童模型1956年首次提出后,就成为学术界的关注焦点,大量学者对此问题进行了研究.在报童问题的模型研究方面,Parlar等[1]在目标函数方面进行了扩展,研究了多目标的报童问题;Petruzzi等[2]和Erlebacher[3]扩展了经典报童问题中的定价决策;宋华明等[4]建立了决策变量为订货点及订货量的正态分布下时变参数的报童问题的数学模型;吴鹏[5]考虑了在回收再制造活动情形下的最优生产量的决策问题;黄宇菲等[6]研究了单位生产成本和单位缺货惩罚成本对报童问题最优解空间的影响.在报童问题约束条件的扩展研究 方面,Vairaktarakis[7]研究了带预算约束的报童问题;Chen等[8]将缺货惩罚转化为一个约束条件,研究正态分布下带订货提前期决策的扩展报童问题;蔡清波等[9]构造了一个带时间决策的推广的报童模型,指出了需求函数的方差是时间的一个线性函数,这种考虑时间的方式,给以后的研究带来了很大的启示;苏菊宁等[10]研究了制造商的生产成本增加量为对称信息和非对称信息条件下的收入共享契约.在供应链问题的研究方面,秦桂英等[11]为优化供应链的运作效率,分析了引入云计算的必要性并给出了具体的实施步骤;翟勇洪等[12]构建了闭环供应链下再制造的生产模型,方便企业选择最优利润决策;Larivier等[13]从渠道协调角度研究了供应链效率的影响因素.本文从供应链角度同时考虑了生产成本和预测精度两个参数随时间变化的报童问题,把缺货损失和过量订货带来的持有成本综合考虑在目标函数中,并对供应链成员间的收益给出了优化协调方案.
1 带时间窗的报童模型
传统的报童模型不考虑时间因素对供应链决策的影响,决策者面临的问题仅仅是如何确定最优的订货批量.考虑到参数随时间变化的特征,订货时点也影响零售商的利润,决策者还要考虑订货时点对自身收益的影响.因此,订货时点和订货量是带时间窗报童模型中的两个决策变量.本文通过引入带时间窗的报童模型,缩短零售商的订货提前期,使得供应链对市场的需求预测更加准确,从而增加供应链的整体收益;并通过引入线性转移系数θ,将零售商收益增加量的一部分转移给制造商,从而实现供应链成员间收益的协调优化.
1.1 模型描述
考虑由一个制造商和一个销售商组成的分散决策型两阶段供应链,生产销售单一的季节性产品.例如时尚服饰的供应和销售,在一个销售期限内,零售商只进行一次订货,零售商的订货量依据对市场需求的预测和供应商发布的订货价格确定.
记X 为产品的市场随机需求,X 是服从正态分布的随机变量,X 的密度函数为f(x,t),分布函数为F(x,t),数学期望μ≡c,c 为常数,记标准正态分布的密度函数、分布函数分别为φ(y),Φ(y).正常情况下,制造商在0时点订货,在带时间窗的报童模型中,制造商与零售商达成压缩订货提前期的契约,零售商此时只需在t 时刻提交订单,此时供应链订货提前期被压缩至T-t.记σ0,σt分别为0时刻和t 时刻零售商对需求预测的均方差.由于订货时点被压缩至t 时刻,零售商可以在[0,t]时间范围内获取更多市场信息,对市场需求的预测精度提高,即σt<σ0,由蔡清波等[9]的研究结果有σ=
相关参数如下:
p 为单位产品的市场销售价格;
c 为制造商的生产成本,c=c0+αt2;
c0为制造商的正常生产成本,即t=0时的生产成本;
α 为提前期压缩一个单位,生产成本的增加量(假设与订货批量无关);
w 为制造商给予零售商的批发价格;
h 为存货带来的费用,如削价处理带来的损失、库存费用等;
s 为单位产品的缺货损失;
T 为零售商从提交订单到收到货物的时间,即提前期;
q 为零售商的订货量;
θ 为收益线性转移系数.
1.2 数学模型
在供应链中,由于供应链各成员间存在信息传递的不对称性,从而导致需求放大现象的存在.本文主要研究基于提前期压缩的供应链收益问题,主要讨论时间和压缩成本对供应链及其成员收益的影响.为方便研究,本文模型假定供应链上下游成员间信息是完全对称的.因此,假设零售商的收益为Πr(q,t),则有
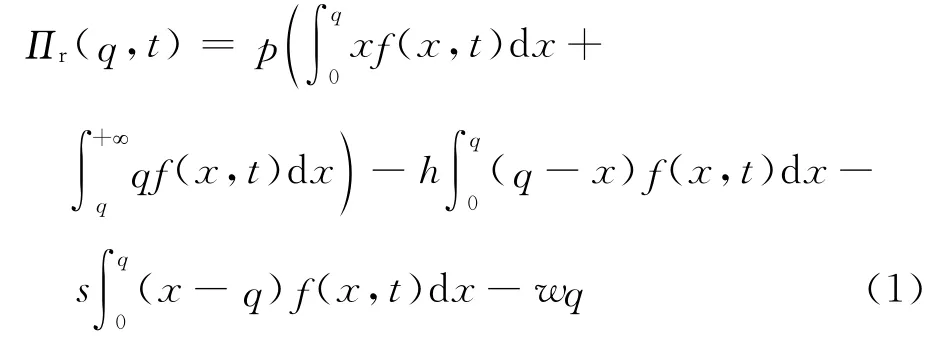
将式(1)简化后,零售商收益为
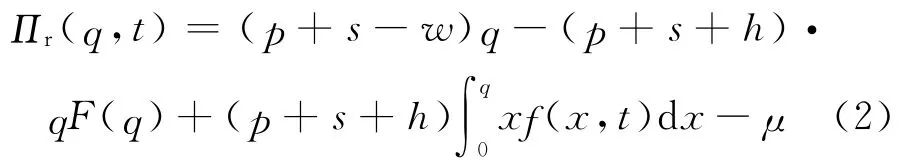
制造商收益为

供应链的整体收益为

式中,F(q)是市场随机需求q 的分布函数;μ 为正态分布函数的数学期望,μ≡c,c 为常数.
2 模型分析
式(2)中,固定变量t,分别对式(2)关于q 求一阶微分和二阶微分,有
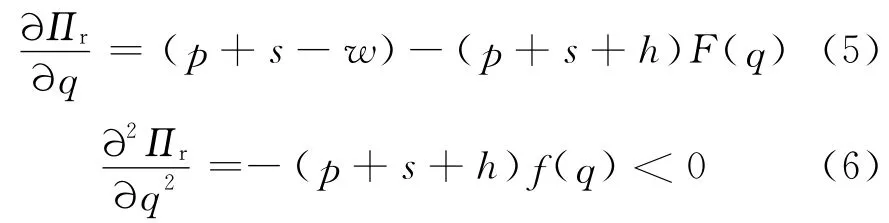
由式(5)和式(6)可知,在订货时间t 时,存在最优订货量使得式(2)取得最大值,令则有

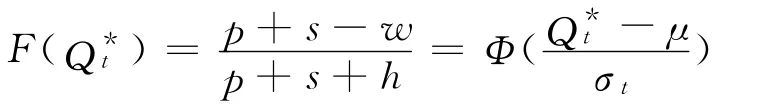
令变量
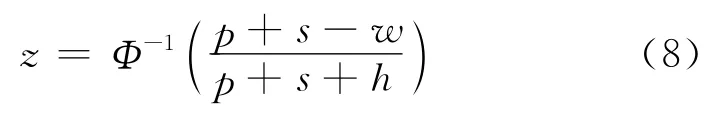
所以
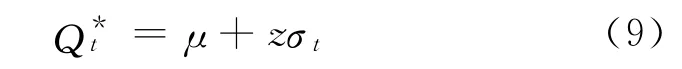
由于在分散决策型供应链中,零售商的最优决策决定整个供应链的订货量,将式(8)和式(9)代入式(2)和式(4),可得零售商的最大收益为

供应链的最大收益为

令t=0,可知零售商正常订货时,零售商收益为
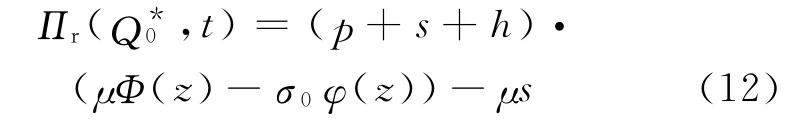
供应链收益为

欲采用压缩订货提前期的方式订货,则需要满足压缩提前期后的供应链收益不低于正常订货时的供应链收益,所以令Δ 为提前期压缩前后的供应链收益变化,则有

即
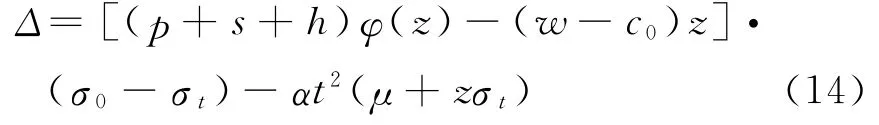
由式(8)可知w=(p+s)-(p+s+h)Φ(z),其中,w∈[c0,p].
令β=(p+s+h)φ(z)-(w-c0)z,则
3 收益协调
与传统不考虑时间因素的报童模型进行比较,带时间窗的报童模型可以给供应链带来更大的利润.但是,零售商独享了时间压缩产生的“溢出”价值,制造商却为此付出了更多的生产成本,导致了自身利润的下降.所以,只有零售商将获得的收益增量的θΔr转移给制造商来弥补由于订货提前期缩短带来的利润损失,制造商才会接受零售商缩短订货提前期的契约.因此,必须对供应链成员间的收益作出协调.
压缩订货提前期后,零售商的收益增加量Δr为

对供应链收益协调后,制造商的收益为

由Δm+θΔr≥0,可知
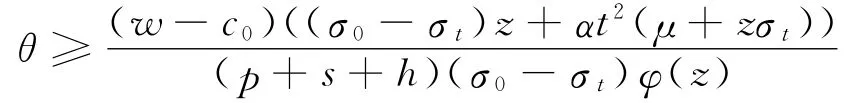
4 数据分析
通过数值算例对上述结果进行验证,在本文模型的假设条件下,假设c0=20,w=40,p=60,T=40,h=10,s=60,μ=100,σ0=20,σT=4.
4.1 α 与时间t的关系分析
计算t 在[0,60]范围内变化时,供应链可承担的最大单位赶工成本增加量,由0 <α <可知,α 的最大临界值为所以令随订货时间点t 变化的情况如图1所示.由图1数据可知,供应链可接受的最大单位赶工成本系数随订货时点的增大而减小,所以在单位赶工成本系数已知的情况下,零售商的订货时间点不是越大越好,在带时间窗的报童模型中存在最佳的订货时点.
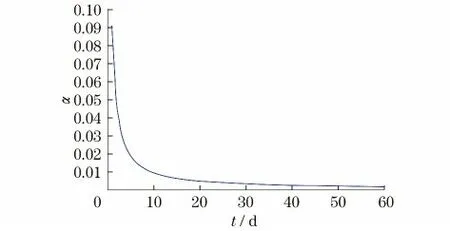
图1 订货时点对最大单位成本增加系数的影响Fig.1 Influence of ordering time on the biggest unit cost increase coefficient
4.2 最优订货量与供应链收益增长率
设定μ,t 为变量,考虑在μ 分别取μ=100,105,110时,供应链的最优订货量随订货时间点t变化的情况,由式(9)可知=μ+zσt=μ+所以可得在不同μ 值情况下随t 的变化情况如图2所示.

图2 不同订货时点下零售商的订货量Fig.2 Retailer’s ordering quantity under different ordering time
由图2可知,随着订货时点的增加,供应链中的企业对市场需求的预测更加准确,所以零售商的订货量随订货时点的增加而减少.此外,订货量随需求函数数学期望的增加而增加.供应链收益增长率设定单位成本增加系数α=0.001 5,则在μ 取不同值时供应链收益增长率随订货时点的变化如图3所示(见下页).由图3可知,在一定订货时点范围内供应链收益增加比例随订货时点的增加而增加,即适当压缩供应链订货提前期可以增加供应链收益.

图3 不同订货时点下供应链的收益增长率Fig.3 Earnings growth of supply chain under different ordering time
4.3 收益协调系数θ与时间t的关系

图4 订货时点对收益转移系数的影响Fig.4 Influence of ordering time on income transfer coefficient
由图中数据可知随着订货时点的增大θmin随之增加,说明制造商因为压缩订货提前期付出了更多的赶工成本,所以零售商需要将更多的额外收益转移给制造商来弥补制造商的损失.订货时点超过一定值后,转移系数大于1,此时供应链收益出现下降,所以确定最优提前期压缩量是确保供应链及其成员收益增加的关键.
5 结 论
讨论了带时间窗的报童决策模型,从供应链的角度来进行优化,通过对供应链及其成员建立收益模型,进行数值分析,并与传统的不考虑时间因素的报童模型进行比较,得出压缩供应链的订货提前期的报童问题比传统报童模型可以给供应链及其成员带来更大的利润.在供应链整体收益增加、制造商生产成本增加的情况下,通过引入线性转移支付系数,实现了制造商与零售商的收益协调.本文假设零售商与制造商的信息是完全对称的,没有考虑信息不对称情况下的收益变化及协调,在以后的研究中可以考虑非对称信息下的报童问题.
[1]Parlar M,Weng Z K.Balancing desirable but conflicting objectives in the newsvendor problem[J].IIE Transanetions,2003,35(2):131-142.
[2]Petruzzi N C,Dada M.Pricing and the newsvendor problem:a review with extensions [J].Operations Research,1999,47(2):183-194.
[3]Erlebacher S J.Optimal and heuristic solutions for the multi-item newsvendor problem with a single capacity constraint[J].Production and Operations Management,2000,9(3):303-348.
[4]宋华明,马士华.正态分布下时变参数的报童问题[J].预测,2005,24(6):67-70.
[5]吴鹏.考虑回收再制造的报童模型扩展[J].清华大学学报(哲学社会科学版),2006,21(S1):71-76.
[6]黄字菲,汪应洛,吕绚丽.报童模型的最优解及其解空间研究[J].运筹与管理,2010,19(5):9-14.
[7]Vairaktarakis G L.Robust multi-item newsboy models with a budget constraint[J].International Journal of Production Economics,2000,66(3):213-226.
[8]Chen M S,Chuang C C.An extended newsboy problem with shortage-level constraints[J].International Journal of Production Economics,2000,67(3):269-277.
[9]蔡清波,鲁其辉,朱道立.预测精度随时间变化的报童问题模型分析[J].预测,2003,22(5):42-45.
[10]苏菊宁,陈菊红,杨变红.基于提前期压缩的非对称信息供应链契约[J].系统工程理论与实践,2009,29(6):39-45.
[11]秦桂英,刘宇熹.基于云计算的供应链运营模式研究[J].上海理工大学学报,2013,35(3):245-250.
[12]翟勇洪,梁玲,刘宇熹,等.面向大规模定制的再制造集约生产计划模型[J].上海理工大学学报,2014,36(6):603-613.
[13]Larivier M A,Porteus E L.Selling to the newsvendor:an analysis of price-only contracts[J].Manufacturing &Service Operations Management,2001,3(4):293-305.

