前景理论框架下基于期望的损失厌恶报童博弈

李新军 康建群（烟台大学，烟台 64005） （大连理工大学，大连 604）

前景理论框架下基于期望的损失厌恶报童博弈

李新军1，2康建群11（烟台大学，烟台 264005）2（大连理工大学，大连 116024）

本文运用前景理论，考虑了损失厌恶报童期望水平对其损失厌恶程度的影响，扩展了损失厌恶报童模型，分析了多个基于期望的损失厌恶报童向一个风险中性供应商竞争订货的情形，研究了报童相关参数对报童均衡总订货量的影响。在随机需求情形下引入期望参考利润水平，首先基于前景理论建立单个基于期望的损失厌恶报童效用函数，其次推导出多个基于期望的损失厌恶报童博弈模型，然后证明了该博弈模型对称纯策略纳什均衡的存在性和唯一性，推导出均衡总订货量的表达式并分析了均衡总订货量与报童数量、损失厌恶系数、期望水平的关系，最后通过算例论证了均衡总订货量与报童数量、损失厌恶系数和期望水平之间关系的正确性，进而比较分析了风险中性报童最优订货量、单个基于期望的损失厌恶报童最优订货量以及均衡总订货量之间的关系。结果表明，均衡总订货量随着报童数量的增多而增加，随着损失厌恶系数的增大而减少，随着期望水平的增大而减少；单个基于期望的损失厌恶报童最优订货量要小于风险中性报童最优订货量以及均衡总订货量。

运作管理 报童模型 前景理论 损失厌恶 博弈理论

引言

1951年，Arrow等人提出的单阶段报童模型，一直以来在运作管理科学领域中被广泛运用和分析，成为随机库存管理问题的经典模型，在诸如产能计划、收益管理和供应链契约等方面近似反映了许多现实生活场景。近年来，报童模型不断加入新的理论、不断出现新的研究视角，其中比较典型的是博弈论在报童模型中的应用以及考虑损失厌恶的报童模型。

博弈理论作为一项重要的分析工具，报童模型被广泛应用于供应链运作管理科学领域。Lippman和McCardle（1997）［1］最早研究了风险中性的报童博弈模型。Cachon（2003）［2］提出了一种按比例分配需求的准则来研究报童博弈模型。Wang（2009）［3］扩展了基于风险中性的报童模型，考虑了多个损失厌恶报童向一个风险中性供应商竞争订货的情形，供应商根据各个报童的订货量按比例分配总需求，则存在一个独特的纳什均衡订货量；需求窃取效应 （Demand－stealing Effect）会增加报童的总订货量，而损失厌恶效应 （Loss Aversion Effect）会减少报童的总订货量，减少的幅度增大时，损失厌恶效应会导致总库存水平降低。李绩才等 （2013）［4］以一个两阶段的供应链系统为研究背景，建立了下游损失厌恶型零售商之间存在竞争的收益共享契约协调模型。

报童模型近年的另外一个热点是假设报童是损失厌恶型，这一假设的提出经过了风险中性——风险厌恶和风险厌恶——损失厌恶两个阶段。报童模型通常假设报童为风险中性，然而，报童在不确定情况下做决策时，其行为会受到自身风险偏好的影响，且大多数决策者对于风险的态度是厌恶的。Neumann和 Morgenstern（1944）［5］在《博弈论和经济行为》中提出了期望效用理论，促使人们用期望效用理论重新研究报童问题。Eeckhoudt等 （1995）［6］在期望效用理论框架下论证了风险厌恶报童的订货量要少于风险中性报童的。Wang等 （2009）［7］论证了风险厌恶报童的订货量随着零售价格的增高而减少。虽然期望效用理论合理解决了在风险条件下报童的决策问题，但是期望效用理论在理论基础和实证研究上均存在问题，且无法解释现实生活中的一些现象，比如买彩票。为了改进期望效用理论以适用于行为运作管理，Kahneman和Tversky（1979）［8，9］提出了前景理论 （Prospect Theory），指出人在作决策时是基于财富变化量的效用，而不是基于总财富的效用，并提出了损失厌恶的概念。Schweitzer和 Cachon（2000）［10］最早在前景理论框架下实证研究了在没有缺货惩罚下的损失厌恶报童问题。Köszegi和Rabin（2006，2007）［11，12］考虑了参照点对报童风险偏好的影响，扩展了损失厌恶报童模型。文平（2005）［13］在前景理论框架下重新研究报童问题，得出损失厌恶报童的最优订货量并进行相关比较静态分析。Wang和Webster（2007）［14］扩展了损失厌恶报童问题，研究 “一个风险中性供应商向一个损失厌恶报童供货”的供应链。Wang和Webster（2009）［15］研究了在前景理论框架下考虑缺货损失的损失厌恶报童问题。邓天虎等 （2009）［16］基于前景理论研究了损失厌恶报童问题最优解的存在性和唯一性。Abeler等 （2011）［17］以及Ericson和Fuster（2011）［18］分别论证了 “当报童有经验或者至少能获得历史数据时，则报童自身风险偏好至少部分受其期望水平的影响”该假设的合理性。柳键等 （2012）［19］基于前景理论分析了损失厌恶零售商订货量与损失厌恶系数、零售价格、采购价格、单位残值、单位缺货损失的关系。Herweg（2013）［20］通过引入一种受报童理性期望影响的内生的报童收益参考水平，构建了基于期望的损失厌恶报童模型，并给出了最优订货量与损失因子、销售价格等参数的关系。Nagarajan等 （2014）［21］证明了前景理论下报童最优订货量与效用参数、权重参数的关系，比较了前景理论下报童最优订货量与经典报童最优订货量。褚宏睿等（2014）［23］研究了回购条件下存在缺货惩罚的损失厌恶报童问题，在需求预测中引入价格因素，推导证明了损失厌恶报童最优订货量与销售价格之间的关系式。

本文在文献 ［3］、文献 ［4］和文献 ［20］的基础上展开，在随机需求情形下引入期望参考利润水平，利用前景理论研究单个基于期望的损失厌恶报童问题，然后根据特定需求分配准则，考虑多个基于期望的损失厌恶报童从一个风险中性供应商那里进行竞争性订货，进而建立博弈模型。文献 ［3］、文献 ［4］的损失厌恶报童考虑了一种固定且外生的参照点，而我们研究了一种受报童理性期望影响的内生的参照点；文献 ［20］研究了单个基于期望的损失厌恶报童问题，而我们研究了多个报童的博弈问题。

1 单个基于期望的损失厌恶报童的效用模型

假设整个销售期间报童无法补货，报童以批发价格w向风险中性供应商进行订货Q。报童零售价格为p，残值为s，且0≤s＜w＜p，不考虑缺货成本。市场需求X是一个随机变量，在连续区间I∈［0，＋∞）上服从概率密度为f（x）的分布，其分布函数是F（x），假定f（x）和F（x）都是可微的。

1.1 风险中性报童的期望利润模型

风险中性报童订货QRN，需求x时的利润为：

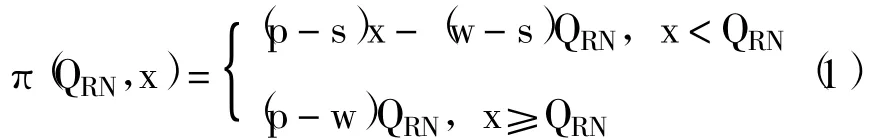
风险中性报童的期望利润为：

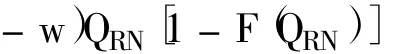
易证，E［π（QRN，x）］是关于QRN的严格凹函数，最大值为且满足

1.2 前景理论框架下基于期望的损失厌恶报童的效用模型

前景理论认为，决策参考点决定决策者对待风险的态度，决策者感兴趣的并不是利润的绝对量，而是相对于某一决策参考点的收益 （Gains）或损失 （Losses）水平。前景理论假定决策者是损失厌恶型——一定数量的损失给决策者带来的痛苦程度要大于同样数量的收益所带来的愉悦程度，增加了损失厌恶系数来表示决策者对待损失的态度。相较于期望效用理论中的效用是总财富效用，前景理论中的效用是财富变化量的效用，即效用是根据参照点的所得与所失得到的，故 Shalev（2000）［24］用如下效用函数讨论博弈论中的多重纳什均衡问题：

其中，π为利润水平，r为参考点，λ≥0为损失厌恶系数。

Köszegi和Rabin（2006，2007）和Herweg（2013）认为，基于期望的损失厌恶报童的整体效用由内生效用和增益损失效用组成。基于期望的损失厌恶报童订货QLA，由于不考虑缺货成本，故报童获得的最高利润是πmax＝（p－w）QLA。为了分析方便，假定期望参考利润R等于最高利润πmax的一定比例，即R＝kπmax＝k（p－w）QLA，其中k是报童期初预估的期望水平，0＜k≤1。

所以，前景理论框架下基于期望的损失厌恶报童的效用函数为：

当x＜QLA时，基于期望的损失厌恶报童的效用函数为：

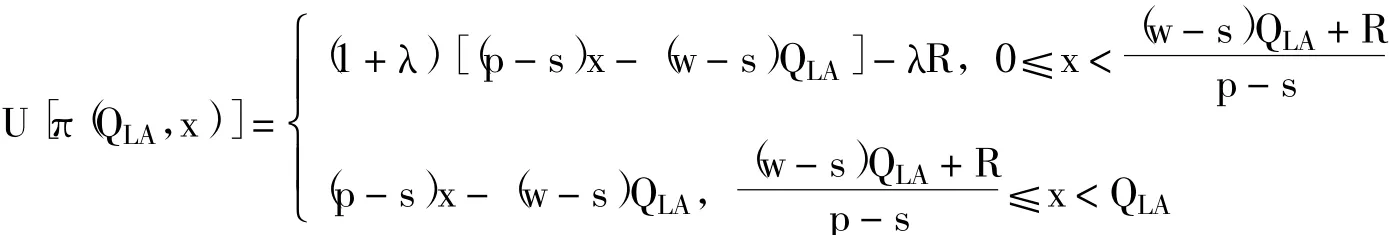
当x≥QLA时，基于期望的损失厌恶报童i的效用函数为：

综合上述两种情况，基于期望的损失厌恶报童的期望效用函数为：

易证，E［U（π（QLA，x））］是关于QLA的严格凹函数，最大值为，且满足

2 多个基于期望的损失厌恶报童的博弈模型

上一节分析单个基于期望的损失厌恶报童的情形，本节研究多个基于期望的损失厌恶报童的博弈问题，假设市场上存在n＞1个同质且相互竞争的基于期望的损失厌恶报童。报童i面对的需求Xi是一个随机变量，在连续区间I∈［0，＋∞）上服从概率密度为g（xi）的分布，其分布函数是G（xi），假定G（xi）是可微、可逆的，并且在区间I上严格递增。若Qi是报童i的订货量，则Q－i是其余 （n－1）个报童总订货量。

根据1.2可知，基于期望的损失厌恶报童i的期望效用函数为

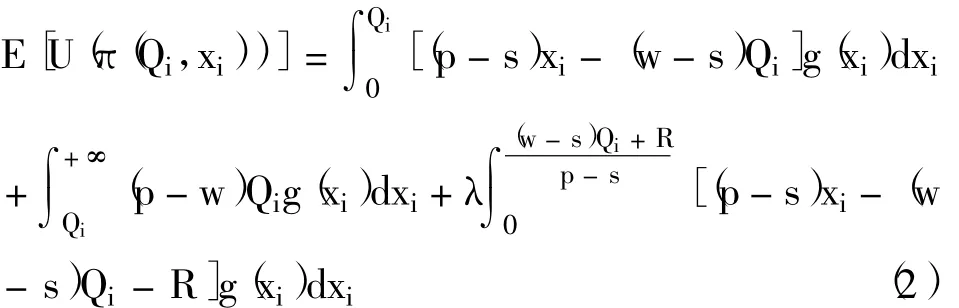
假设市场需求X根据各报童的订货量按比例进行划分，则报童i的需求Xi为：

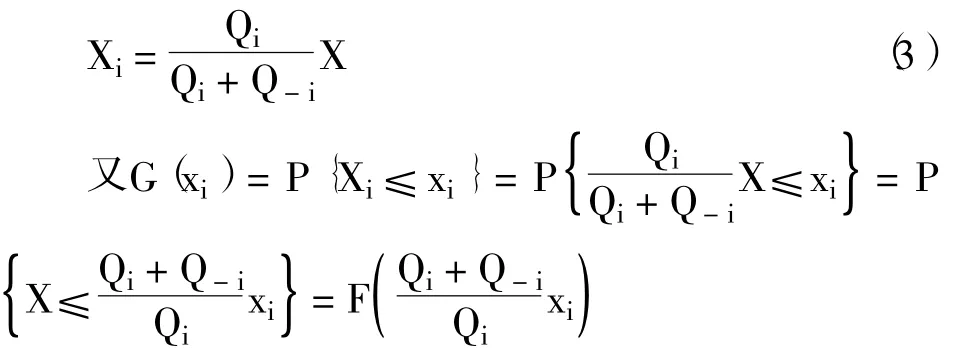
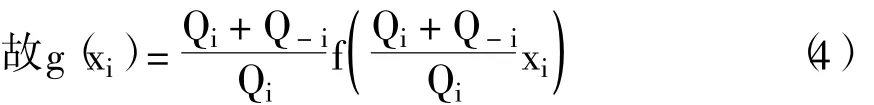
将式 （3）和式 （4）代入式 （2），整理可得：

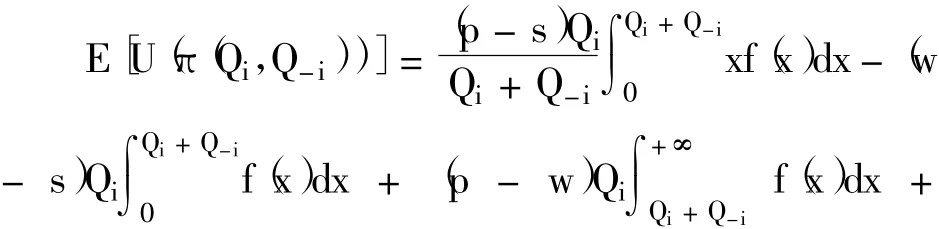
其中，

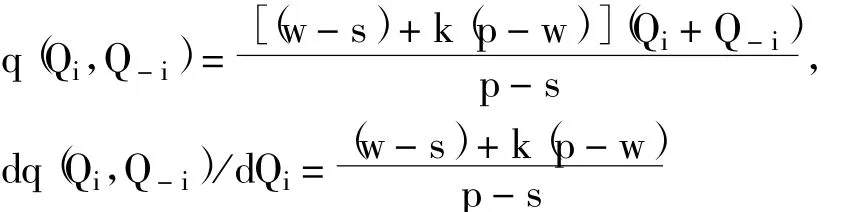
定理1：对于任意Q－i≥0，基于期望的损失厌恶报童i的期望效用函数E［U（π（Qi，Q－i））］是Qi的凹函数，最优订货量Q*i（Q－i）满足如下条件：

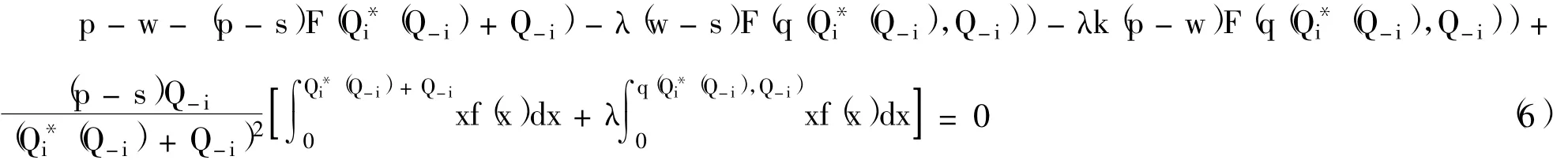
证明：对式 （5）分别求关于Qi的一阶偏微分和二阶偏微分，得：

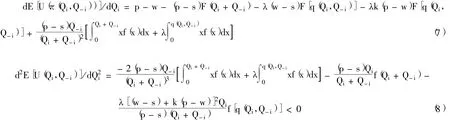
式 （8）表明E［U（π（Qi，Q－i））］是Qi的凹函数，所以存在一个最优订货量Q*i（Q－i）使得期望效用最大，并且满足式 （6）。

定理1刻画了基于期望的损失厌恶报童i在面对其他 （n－1）个报童的总订货量Q－i时可做出的最优反应，也就是说，如果给定其余 （n－1）个报童的总订货量Q－i，那么存在一个最优订货量，使得报童i的期望效用最大。

定理2：多个基于期望的损失厌恶报童博弈中，至少存在一个对称纯策略纳什均衡。

证明：根据纳什均衡存在定理［25］，在n人策略博弈中，纯策略纳什均衡存在的充分条件是：（ⅰ）每个参与人的纯策略空间Si是欧氏空间上一个非空的、闭的、有界的凸集；（ⅱ）每个参与人的支付函数Ui（si）是连续的；（ⅲ）支付函数Ui（si）对si是拟凹的。

在策略博弈过程中，报童们同时决定他们各自的策略，即订货量，Qi∈σ＝［0，S］，其中σ是报童的策略空间，S充分大以保证不会限制报童们的选择。（1）我们通过选择一个足够大、有界、闭的凸集［0，S］×［0，S］×…×［0，S］来实现条件（ⅰ）；（2）因为我们假定n个报童的总需求X的分布函数F（x）是连续的，那么基于期望的损失厌恶报童i的期望效用函数E［U（π（Qi，xi））］是连续的，所以满足条件 （ⅱ）；（3）根据定理1可知，E［U（π（Qi，xi））］是Qi的凹函数，所以满足条件（ⅲ）。因此，基于期望的损失厌恶报童博弈中，至少存在一个纯策略纳什均衡，又所有报童都是同质的，所以这个纯策略纳什均衡是对称的。

定理3：多个基于期望的损失厌恶报童博弈中，对于n个报童而言，他们的订货量存在唯一的纳什均衡特别地，对于任意i∈［1，2，…，n］，报童i的唯一均衡订货量满足其中，n个报童唯一的均衡总订货量Q*应使得下式成立：

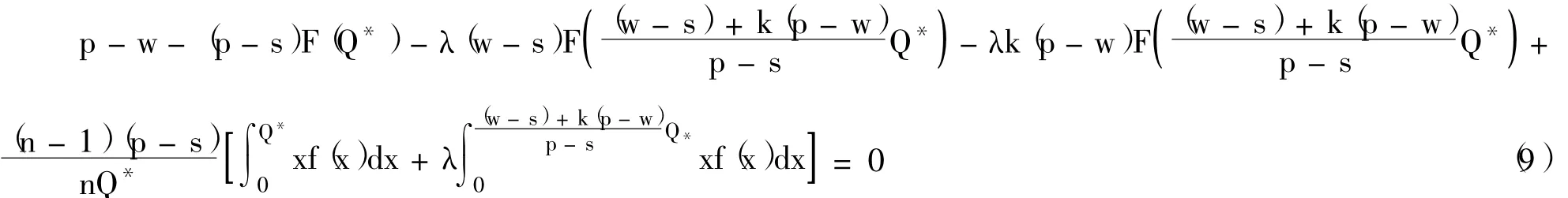
证明：由于对任一报童i，其最优订货量（Q－i）都有式 （6）成立，且n个零售商之间是同时决定各自订货量的纳什博弈。根据对称性，如果存在纳什均衡解，则必然有成立。显然

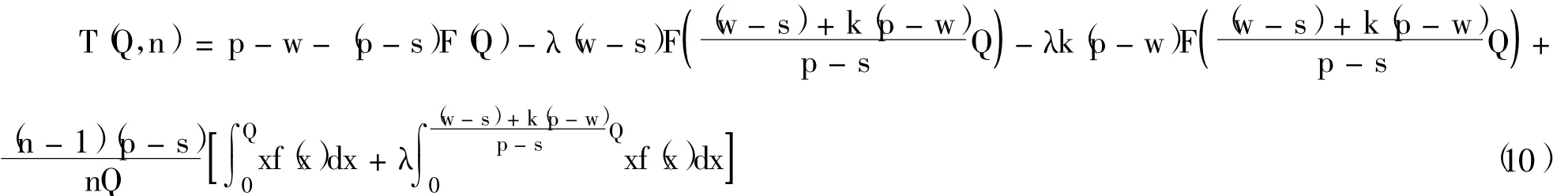
很明显，T（Q，n）对Q的一阶导数为负，即：

可知，T（Q，n）是Q的严格减函数。又因为：

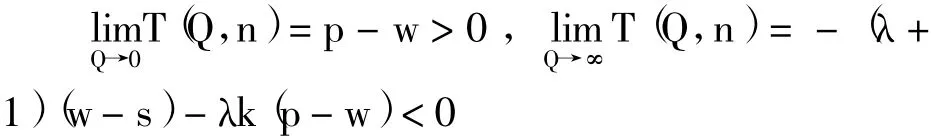
存在唯一的均衡总订货量Q*＞0使得T（Q，n）＝0，即满足式 （9）。所以，在n个基于期望的损失厌恶报童博弈中，n个报童的订货量存在唯一的纳什均衡

推论1：多个基于期望的损失厌恶报童的均衡总订货量Q*随着报童数量n的增加而增加。

证明：对于任意n2＞n1＞1，令分别代表n1和n2个报童的均衡总订货量。由定理3可知，根据式 （10），易得那么T又因为T（Q，n）是Q的严格减函数，可得，当n2＞n1＞1时，也就是说，均衡总订货量Q*随着报童数量n的增加而增加。

推论1表明，供应链中报童的数量越多，整个供应链的库存水平就越高，这与Cachon（2003）的风险中性报童博弈模型的结论一致。由于需求偷窃效应的影响，即某一报童订得越多，其他报童面临的随机需求将越少，所以报童的数量越多，报童之间的竞争程度将越激烈，从而增加了总订购量，提高了整个供应链的库存水平。

推论2：多个基于期望的损失厌恶报童的均衡总订货量Q*（基于期望的损失厌恶报童i的均衡订货量随着损失厌恶系数λ的增大而减少。

证明：根据式 （9），由隐函数求导可知，

所以，dQ*／dλ＜0，即均衡总订货量Q*随着损失厌恶系数λ的增大而减少。又所以基于期望的损失厌恶报童i的均衡订货量也随着损失厌恶系数λ的增大而减少。

推论2表明，损失厌恶效应会减少报童们的总订货量，也就是说，策略博弈中报童们的损失厌恶程度越强，均衡总订货量将越少。

推论3：多个基于期望的损失厌恶报童的均衡总订货量Q*随着期望水平k的增大而减少。

证明：同理，根据式 （9），由隐函数求导可知，

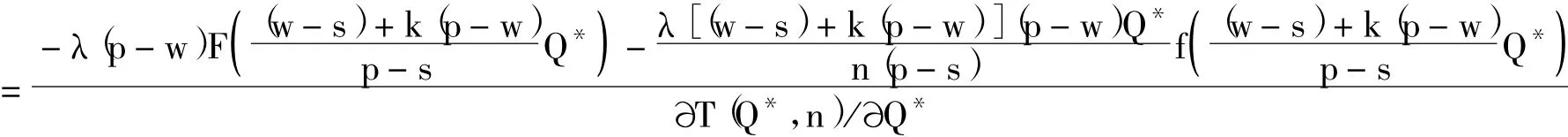
因为p＞w＞s≥0，Q*＞0，λ＞0以及T（Q*，n）／Q*＜0，所以，dQ*／dk＜0，即均衡总订货量Q*随着期望水平k的增大而减少。

推论3表明，期初报童的期望参考利润水平设定的越高，均衡总订购量将越少，也就是说，期初报童越期望获得高利润，越可能面临心理落差，从而增益损失效用越小，导致均衡总订货量越少。

3 算例分析

下面通过一个数值算例进一步分析报童的相关参数对均衡总订货量的影响，并对上述模型推导得出的各种主要最优订货量进行分析。

假定模型参数为零售价格p＝12，批发价格w＝6，回收价格s＝2，报童数量n取1～10之间的整数，损失厌恶系数λ介于0～5之间，期望水平k介于0～1之间。为了方便分析问题，假设市场总需求X服从均匀分布X～U［0，100］，其密度函数为

基于给出的参数赋值，首先分析报童的相关参数对均衡总订货量的影响，计算结果如表1～表3所示。

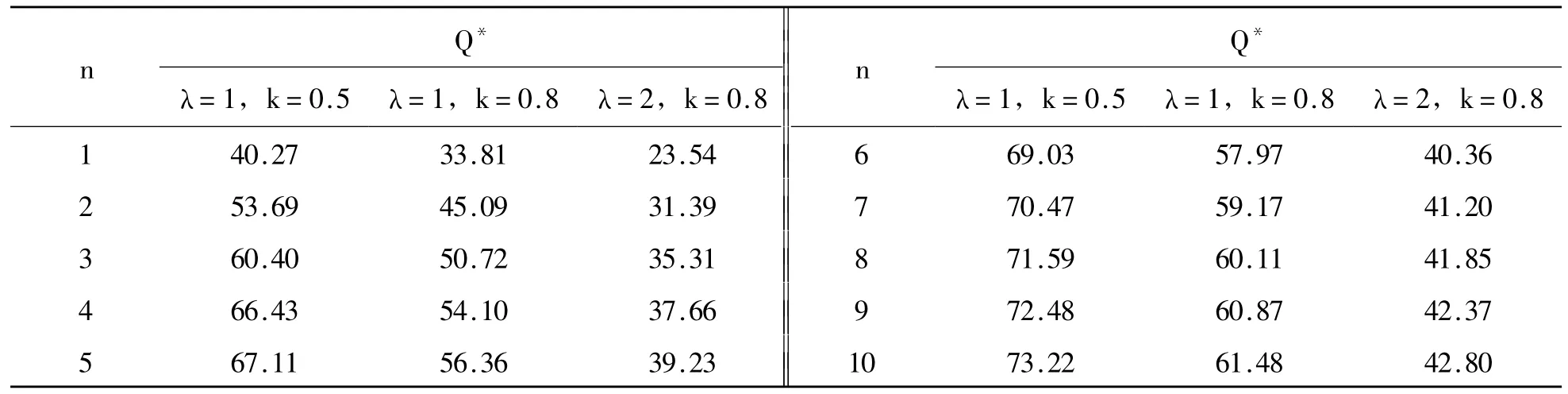
表1 报童数量和均衡总订货量

从表1可以看出，报童数量的增加会使均衡总订货量不断增加，因为报童数量的增加会加剧报童之间的竞争，需求偷窃效应会增强，报童们会纷纷增加其订货量以抢占市场需求，进而使得均衡总订货量增加。当报童数量在5个以下时，均衡总订货量增加很快，但当报童数量继续增加时，均衡总订货量增加速度明显变慢，并逐渐趋于平稳。损失厌恶系数和期望水平的增大会抵消报童数量对均衡总订货量的影响，比如λ＝1，k＝0.8和λ＝2，k＝0.8，λ＝1，k＝0.5和λ＝1，k＝0.8（如图1所示）。

图1 报童数量影响均衡总订货量示意图

从表2可以看出，均衡总订货量随损失厌恶系数的增大而减少，因为当不考虑缺货损失、只考虑产品剩余损失时，基于期望的损失厌恶报童为了减少损失会减少其订货量，使得均衡总订货量减少。当损失厌恶系数小于1时，均衡总订货量迅速减少，当损失厌恶系数不断增大时，均衡总订货量虽然仍持续减少，但减少的速度放缓。报童数量的增加、期望水平的增大会加重损失厌恶系数对均衡总订货量的影响，比如n＝2，k＝0.8和n＝5，k＝0.8，n＝2，k＝0.5和n＝2，k＝0.8（如图2所示）。

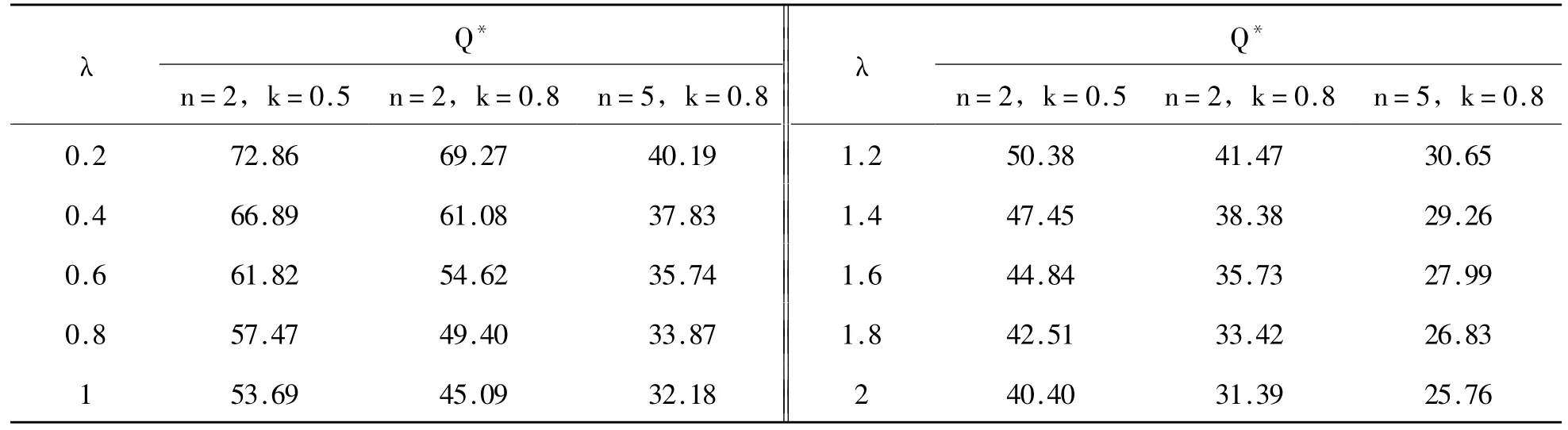
表2 报童损失厌恶系数和均衡总订货量

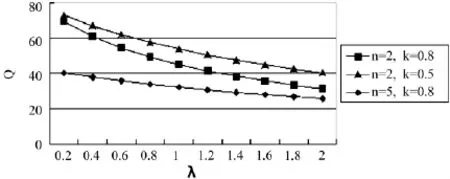
图2 损失厌恶系数影响均衡总订货量示意图

从表3可以看出，基于期望的损失厌恶报童期初对可获得的利润期望越大，均衡总订货量将越少，因为期初报童的期望参考利润水平设置得越高，相较实际获得的利润，报童越容易感到利润损失，而此时报童订得越多，利润损失得越多，进而报童对损失的厌恶促使报童少订货，使得均衡总订货量减少。报童数量的增加会抵消甚至超过报童期望水平对均衡总订货量的影响，比如λ＝1，n＝2和λ＝1，n＝5，报童损失厌恶系数的增大会加重报童期望水平对均衡总订货量的影响，比如λ＝1，n＝2和λ＝2，n＝2。从图3可以看出，期望水平对均衡总订货量的影响呈现出一种近乎线性的平稳状态，这与前文期望水平的设定有关。

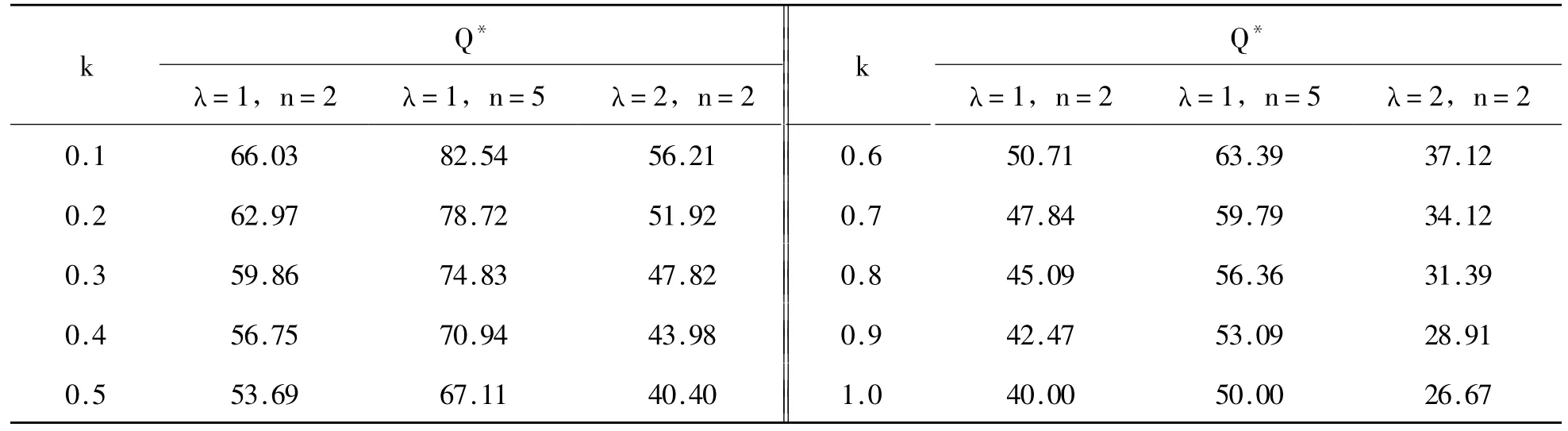
表3 报童期望水平和均衡总订货量

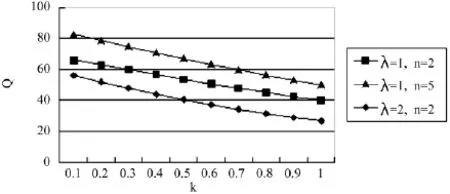
图3 期望水平影响均衡总订货量示意图

根据上述分析，下面通过数值计算对前文风险中性报童最优订货量、单个基于期望的损失厌恶报童最优订货量以及均衡总订货量分别进行数值计算，计算结果如表4所示。

表4 最优订货量

当多个基于期望的损失厌恶报童在市场上互相竞争时，报童间的需求偷窃效应使均衡总订货量Q*普遍大于而且报童数量越多，两者之间的差值一般越大。报童损失厌恶系数越大、期望水平越大，均衡总订货量Q*与之间的差值将越小。均衡总订货量Q*一般小于Q*SRN，但当报童损失厌恶系数和期望水平较低而报童数量较多时，均衡总订货量有可能大于风险中性报童最优订货量。

4 结 论

传统报童模型通常假定报童是风险中性的，但在现实生活中，规模较小的供应链参与主体往往规避风险或损失。假设报童是损失厌恶的并且追求效用最大化，运用前景理论得到基于期望的损失厌恶报童的效用函数，并将单个报童扩展到n个报童，构建了多个基于期望的损失厌恶报童博弈模型。文章得出多个竞争性报童存在唯一的纳什均衡总订货量Q*，推出Q*随报童数量的增加 （即竞争程度的增大）而增加、随报童损失厌恶程度的增大而减少以及随报童期望水平的增大而减少。通过算例验证了上述结论并发现：单个基于期望的损失厌恶报童最优订货量普遍小于风险中性报童最优订货量，而且报童损失厌恶系数越大、报童期望水平越大，两者的差值越大；均衡总订货量普遍大于单个基于期望的损失厌恶报童最优订货量，而且报童数量越多，两者的差值一般越大，报童损失厌恶系数越大、期望水平越大，两者的差值将越小；均衡总订货量一般小于风险中性报童最优订货量，但当报童损失厌恶系数和期望水平较低而报童数量较多时，均衡总订货量有可能大于风险中性报童最优订货量。

本文只考虑了供大于求时产品剩余所产生的损失风险，没有考虑缺货损失对于基于期望的损失厌恶报童订货决策产生的影响，而缺货损失为产品数量的线性、非线性函数情形下对于报童决策的影响以及缺货损失对于供应链中多个基于期望的损失厌恶报童博弈结果等方面的影响，有待进一步研究。

［1］Lippman SA，McCardle K F.The Competitive Newsboy［J］.Operations Research，1997，45：54～65

［2］Cachon G P.Supply Chain Coordination with Contracts［M］.In：de Kok AG，Graves SC（Eds.），Handbook in Operations Research and Management Science，Volume on Supply Chain Management：Design，Coordination and Operation.North Holland，Amsterdam，2003：229～339

［3］Charles XWang.The Loss－averse Newsvendor Game［J］.Productions Economics，2009，124：448～452

［4］李绩才，周永务，肖旦，等.考虑损失厌恶一对多型供应链的收益共享契约 ［J］.管理科学学报，2013，16（2）：71～82

［5］Von Neumann，Morgenstern.博弈论与经济行为 ［M］.上海：三联书店，2004

［6］Eeckhoudt L，Gollier C，Schlesinger H.The Risk－averse（and prudent）Newsboy［J］.Management Science，1995，41：786～794

［7］Wang C X，Webster S，Suresh N C.Would a Risk－averse Newsvendor Order Less at a Higher Selling Price？ ［J］.European Journal of Operational Research，2009，196：544～553

［8］Kahneman D and Tversky A.Prospect Theory：An Analysis of Decision under Risk［J］.Econometrica，1979：263～291

［9］Tversky A and Kahneman D.Advances in Prospect Theory：Cumulative Representation of Uncertainty［J］.J.Risk Uncertainty，1992：297～323

［10］Schweitzer M，Cachon G.Decision Bias in the Newsvendor Problem with a Known Demand Distribution：Experimental Evidence［J］.Management Science，2000，46（3）：404～420

［11］Köszegi，B，Rabin M.A Model of Reference－dependent Preferences［J］.Quarterly Journal of Economics，2006，121：1133～1165

［12］Köszegi，B，Rabin M.Reference－dependent Risk Attitudes［J］.American Economic Review，2007，97：1047～1073

［13］文平.损失厌恶的报童——预期理论下的报童问题新解［J］.中国管理科学，2005，13（6）：64～68

［14］Wang C X，Webster S.Channel Coordination for a Supply Chain with a Risk－neutral Manufacturer and a Loss－averse Retailer［J］.Decision Sciences，2007，38，361～389

［15］Wang C X，Webster S.The Loss－Averse Newsvendor Problem［J］.Omega，2009，37（1）：93～105

［16］邓天虎，黄四民.基于预期理论的报童模型及敏感性分析［J］.管理评论，2009，21（6）：108～112

［17］Abeler J，Falk A，Goette L，Huffman D.Reference Points and Effort Provision［J］.The American Economic Review，2011，101：470～492

［18］Ericson KM M，Fuster A.Expectations as Endowments：Evidence on Reference－dependent Preferences from Exchange and Valuation Experiments［J］.The Quarterly Journal of Economics，2011，126：1879～1907

［19］柳键，邱国斌，黄健.考虑缺货损失情形下损失厌恶零售商的订货决策 ［J］.控制与决策，2012，27（8）：1195～1199

［20］Herweg F.The Expectation－Based Loss－Averse Newsvendor［J］.Economics Letters，2013，120（3）：429～432

［21］Nagarajan M，Shechter S.Prospect Theory and the Newsvendor Problem［J］.Management Science，2014，60（4）：1057～1062

［22］王怡，等.绿色供应链企业知识共享战略联盟动态博弈研究——帕累托有效协同视角 ［J］.工业技术经济，2013，（3）：61～66

［23］褚宏睿，冉伦，李金林，等.带有回购和缺货惩罚的损失厌恶报童问题 ［J］.管理评论，2014，26（4）：101～109

［24］Shalev，J.Loss Aversion Equilibrium［J］.Int.J.Game Theory，2000，29：269～287

［25］张维迎.博弈论与信息经济学 ［M］.上海：上海人民出版社，2004：67～75

Expectation－based Loss－averse Newsvendor Game Based on Prospect Theory

Li Xinjun1，2Kang Jianqun1
（1.Yantai University，Yantai264005，China；2.Dalian University of Technology，Dalian 116024，China）

Based on prospect theory，this paper considers the influence of loss－averse newsbvendor's expectation level on the degree of loss aversion，extends the loss－averse newsvendor model to a game setting where multiple expectation－based loss－averse newsvendors are competing for inventory from a risk－neutral supplier and researches the influence of newsvendor's related parameterson the equilibrium total quantity.Introducing expectation reference profits under stochastic demand，this paper firstly uses prospect theory to establish the utility function of a single expectation－based loss－averse newsvendor，secondly deduces the gamemodel ofmultiple expectation－based loss－averse newsvendors，then proves the existence and uniqueness of pure strategy Nash equilibriumh in the gamemodel，deduces the expression of the equilibrium total quantity and analyzes the relationship between the equilibrium total quantity and newsvendor number，loss－averse coefficient，expectation level，finally demonstrates the correctnessof the relationship through numericalexample and compares the risk－neutral newsvendor's optimal order quantity，the optimal order quantity of a single expectation－based loss－averse newsvendor with the equilibrium total quantity.We find that the equilibrium totalquantity increaseswith the newsvendor number，and decreaseswith the loss－averse coefficient，and decreaseswith the expectation level.Moreover，the optimalorder quantity ofa single expectation－based loss－averse newsvendor is smaller than risk－neutral newsvendor's optimal order quantity and the equilibrium total quantity.

operationmanagement；newsvendormodel；prospect theory；loss averse；game theory

10.3969／j.issn.1004－910X.2016.01.005

F253；F273

A

（责任编辑：王 平）

2015—10—18

国家社科基金项目 “基于供应商产能的供应应急策略与设计研究”（项目编号：12CGL042），国家自然科学基金资助项目“以DC为中枢的农产品冷链库存策略与多温共配优化研究”（项目编号：71372122），国家自然科学基金项目 “考虑有限理性的供应链中断风险管理模型研究”（项目编号：71272122）。

李新军，烟台大学经济管理学院副教授，大连理工大学管理与经济学部博士后。研究方向：物流与供应链管理，应急管理，运作管理。康建群，烟台大学经济管理学院硕士研究生。研究方向：应急管理。