未知视觉参数下的移动机器人动力学鲁棒镇定
王 刚, 王朝立, 杜庆辉, 季云峰
(1.上海理工大学 管理学院,上海200093;2.上海理工大学 光电信息与计算机工程学院,上海 200093)
轮式移动机器人是典型的具有非完整约束的系统,近三十年来已经引起越来越广泛的关注[1-2].由于非完整系统不满足Brockett定理[3]的3个必要条件,因此不存在光滑时不变纯状态反馈律使其镇定,故许多经典的线性系统方法无法直接应用于移动机器人的镇定问题上.为了解决这个问题,大量的学者在这方面作了相关的研究,如使 用 滑 模 控 制[4-5]、转 换 为 链 式 系 统[6-7]、使 用 不连续的反馈[8]以及光滑时变反馈[9]等.为了控制移动机器人,通常假设机器人的各个状态是精确知道的,但在实际中,由于测量的精度和一些不确定的干扰,这个假设是很难成立的.利用视觉反馈获得控制器所需要的位置信息是克服这些问题的一种有效办法.
近年来,视觉反馈已经被广泛地应用在机器人的控制上[10-11].回顾以往文献,缺乏深度信息是单目视觉伺服固有的缺点.Dixon等[12]利用放置在天花板上不校调的单目摄像机设计了自适应跟踪控制器,实现了机器人的跟踪控制.最近,Fang等[13]和Chen等[14]通过分解单应矩阵分别设计了自适应镇定控制器和跟踪控制器,用以补偿未知的深度信息,实现了移动机器人的渐进镇定和跟踪.但是由于对目标机器人线速度和角速度等的限制,文献[12]和[14]无法解决移动机器人的镇定问题.同时,对于单应矩阵的分解也是非常复杂的,常常需要人为干预.Mariottini等[15]提出了基于图像的控制策略,通过控制极线几何中的极点,实现了移动机器人的镇定.但利用极线几何的缺点是短基线时候的准确性降级以及对于平面场景呈现病态.文献[16]研究了移动机器人在运动过程中保证特征点不出视野的问题,同时不需要分解单应矩阵.而Fang等[17]把云台摄像机放置在移动机器人上,提出了新的主动视觉控制算法.该算法包含两个控制器:一个控制云台摄像机旋转使得特征点始终保持在图像中央;一个控制机器人使其镇定.彭飞等[18]探讨了针对车载单目摄像机的轮式移动机器人的目标跟踪问题.
本文主要探讨未知视觉参数下的移动机器人的镇定问题.主要贡献有两点:一是对于单目摄像机模型下的移动机器人运动学模型,设计了期望的运动速度,实现了机器人的指数镇定;二是对于带有不确定扰动的非完整移动机器人的动力学,利用计算力矩法设计力矩控制器,实现了机器人的实际速度在有限时间内收敛至期望速度.
1 问题的描述
1.1 系统配置
本文研究的视觉反馈下的非完整移动机器人模型如图1所示.假设单目摄像机固定在天花板上,且摄像机图像平面与机器人运动平面平行.构造3个坐标系,分别是世界坐标系X-Y-Z、摄像机固连坐标系X1-Y1-Z1以及图像坐标系u-o-v.假设图像坐标平面u-v 和摄像机坐标系X1-Y1平面平行.点C 是摄像机光轴与X-Y 平面的交点,在X-Y 平面上的投影是(px,py),摄像机坐标系坐标原点在图像平面的坐标为(Oc1,Oc2).同时,坐标(x,y)是机器人质心P 在X-Y 平面的坐标,(xm,ym)为(x,y)在图像坐标系下的投影.θ 表示机器人前向与X 轴的夹角.则摄像机投影模型为[12]

式中,α1,α2为与深度信息、光轴长度以及沿x 轴和y 轴缩放因子有关的未知的正常数.R 定义如下:
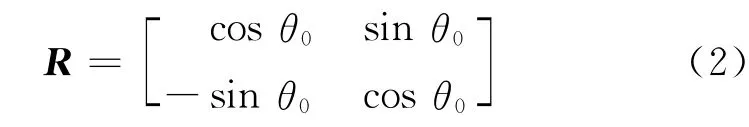
式中,θ0表示摄像机坐标系与世界坐标系沿逆时针方向的夹角.
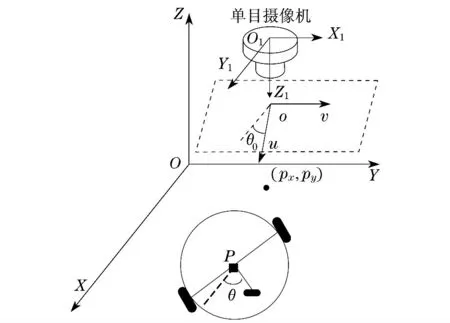
图1 单目摄像机-机器人系统Fig.1 Camera-robot system configuration
1.2 移动机器人的动力学以及运动学
利用Euler-Lagrangian公式可以将带有非完整约束的机械系统描述成[4,19]

式中,q∈ℝn是广义坐标;τ∈ℝr表示控制输入;κ∈ℝm表示约束力向量;M(q)∈ℝn×n表示正定对称惯性矩阵表示向心力和哥氏力;G(q)∈ℝn是重力向量;B(q)∈ℝn×r是输入变换矩阵;A(q)∈ℝm×n是和约束条件有关的矩阵.为了简化接下来的分析,假设r=n-m.同时由于机器人作平面运动,因此G(q)=0.
移动机器人的非完整约束可以表述成

同时取

式中,S(q)∈ℝn×(n-m)=ℝn×r是由A(q)解空间中一组基组成,z=[z1,…,zn-m]T与内部的状态变量相对应.对式(5)两边微分并利用式(3),移动机器人的动力学可以被重写成
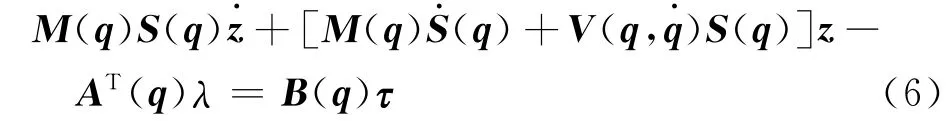
式(6)两边左乘ST(q),利用ST(q)AT(q)=0,可以得到
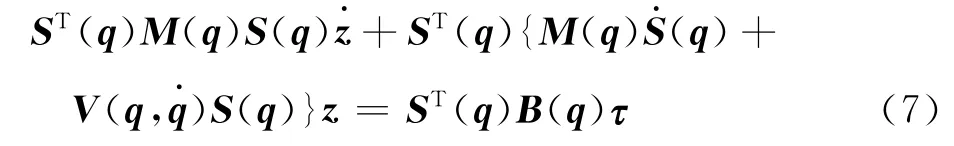
左乘[ST(q)B(q)]-1,式(7)可以简化为
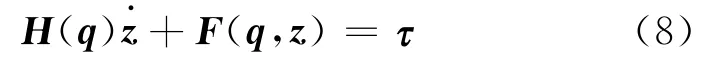
式中,

对于(2,0)型移动机器人来说,式(5)中q 和z分别为q=[x,y,θ]T,z=[ν,ω]T.其中x,y,θ 前面已经指出其物理意义,而ν,ω 分别表示移动机器人的线速度和角速度.接下来对带有不确定扰动的机器人动力学作如下假设[4].
假设1 带有不确定扰动的移动机器人的动力学可以表述成
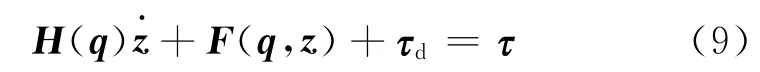
式中,τd=H(q)f 为机器人所受的不确定扰动;f=是机器人左右轮的输入力矩.
对于图1所示的(2,0)型移动机器人,假设其质心和几何中心重合,并且其固定轮在平面上做纯滚动无侧滑运动.具有这样约束条件的移动机器人的运动学模型在世界坐标系下可表示为

通过式(1)和式(10),可以得到机器人在图像坐标系下运动学模型
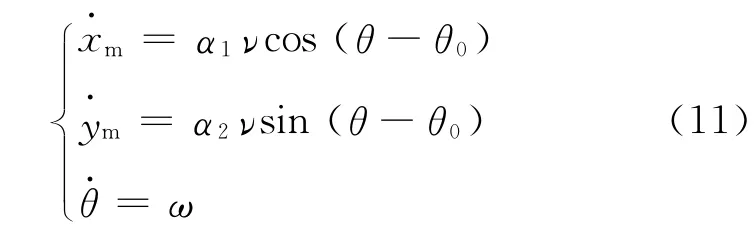
2 控制器设计
为了简化接下来的分析,做如下假设.
假设2 θ0是已知的,α1=α2=α 是未知的,且存在一个已知的正常数,使得

把(θ-θ0)用θ 替换,式(11)可以被重写成

对式(12)作如下全局可逆变换可得

根据式(12)和式(13),得到

通过观察,利用线性系统理论易证θ 可以通过ω 全局指数收敛到零,但是这样会造成状态量η1,η2不可控.为了避免这个问题,引入状态缩放
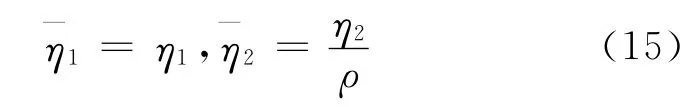

根据非完整链式系统设计方法[9,20]和前面的分析,设计期望的运动速度如下:
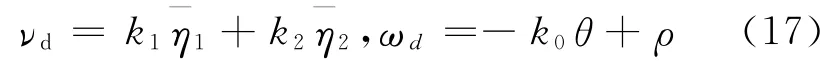
式中,ki(i=0,1,2)是待设计的参数.
定义如下速度误差信号
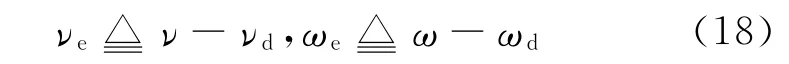
由于式(9)中H(q),F(q,z)中的系数只与θ 有关而与x,y 无关[21-22].这样只要θ 从摄像机中获得,那么H(q),F(q,z)就是已知的.利用计算力矩法[23],力矩控制器可以选择为
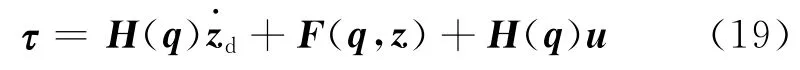
式中,zd=[νd,ωd]T,u(t)=[u1,u2]T是相应的控制输入.基于接下来稳定性分析,定义控制输入u(t)如下:

式中,0<p1,p2<1,且

下面来证明要用到的几个引理.
引理1[24]假设存在连续函数V(t),满足以下条件:
a.V 是正定的;
b.存在正常数c 和β∈(0,1),使得

那么存在一个时间点T0,使得当t ≥T0时,V (t) ≡0,其中
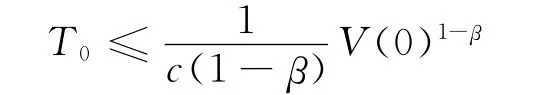
引理2[25]矩阵A∈ℝ2×2,矩阵A 的特征多项式为那 么 矩 阵A 是Hurwitz矩阵的充要条件是a1,a2>0.
引理3[26]考虑线性时变系统

如果矩阵A1∈ℝn×n是Hurwitz矩阵,且A2(t)满足以下条件:
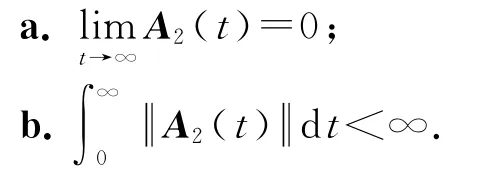
那么系统(23)是指数稳定的.
定理1 对于系统(12),选择控制器(19)并且当参数ki(i=0,1,2)满足以下条件时:
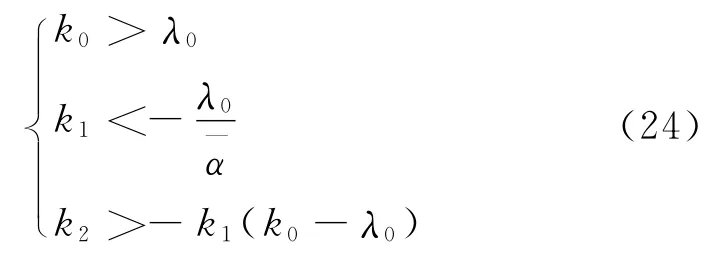
证明 式(19)减去式(9),得到
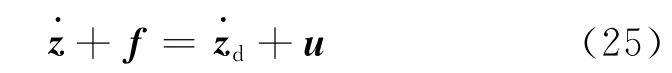
把式(18)代入式(25),利用式(20)
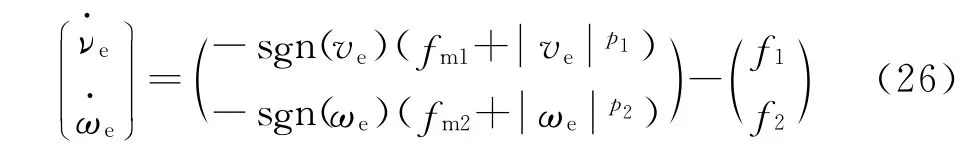
构造非负标量函数Vν

利用式(26),对式(27)求微分
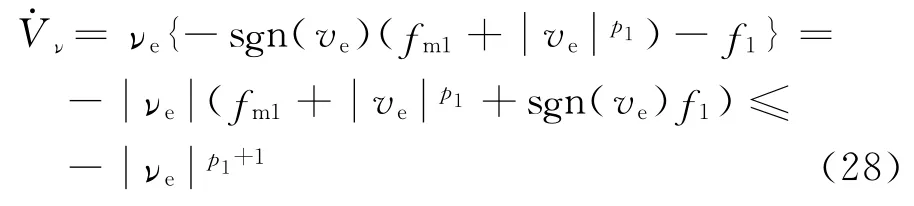
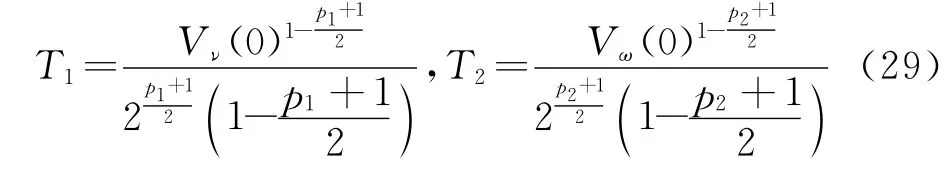
显然Vν(0)和Vω(0)有界,则当t≥max{T1,T2}时,由于νe≡0,ωe≡0.利用式(17)和式(18)
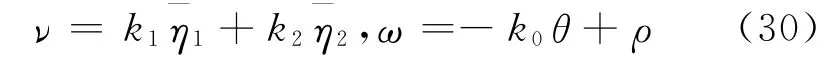
式(30)代入到式(16)的第三个方程,有

对式(31)解微分方程
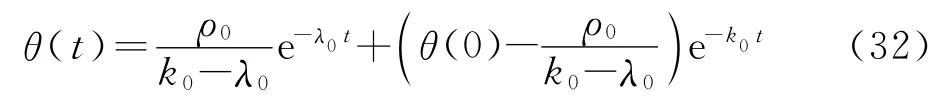
式中,θ(0)是θ 的初始值.式(30)和式(32)表明θ,ω 将会指数收敛至零.
将式(30)和式(32)代入到式(16)的第一和第二个方程中,可以得到
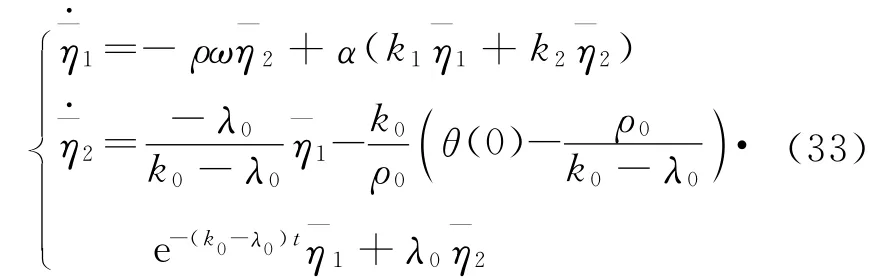
基于接下来的分析,把式(33)写成如下矩阵形式

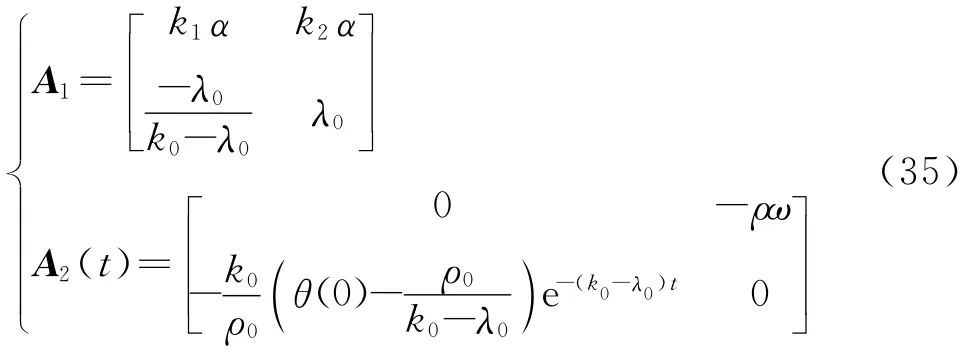
矩阵A1的特征多项式
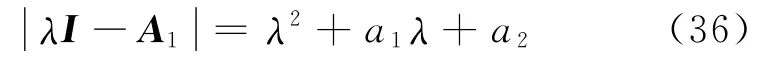
由于k1,k2满足式(24),这样a1>0,a2>0.因此,由引理2 可知A1是Hurwitz矩阵.由于ρ,ω 都将指数收敛到零,同时,由式(24)的第一个不等式条件可以看出矩阵A2(t)的每个元素γij(i,j=1,2)都将指数收敛到零.当时,由引理3可知,系统(16)是指数稳定的.此外,由于ρ(t)是指数收敛的,所以η1,η2 也会指数收敛到零.综上所述,利用力矩控制器(19),当t≥max{T1,T2}时,系统(12)将会指数收敛至其期望位姿.至此,完成了定理1的证明.
3 仿 真
对于系统(12)选择初始值

设置参数λ0=1,ρ0=1,α—=1,α=1.5,fm1=1,fm2=1,不确定扰动是[-1,1]范围内的随机数.根据控制条件(20)和(24),选择p1=0.5,p2=0.5,k0=1.5,k1=-2,k2=2.那么机器人的状态量如图2—5所示.仿真结果验证所提控制器的有效性.此外,如果选择k1,k2,k3是矩阵A1的特征值在复平面中左半平面远离虚轴,选择p1,p2使得T1,T2尽可能的短,则系统(12)收敛的速度更快.
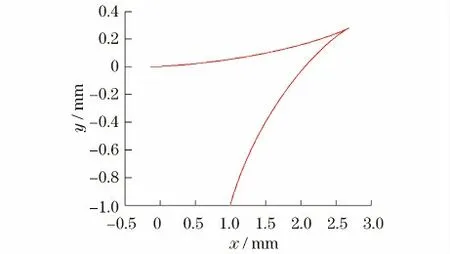
图2 机器人在图像坐标系下的运动轨迹Fig.2 Trajectory of the robot in the image frame
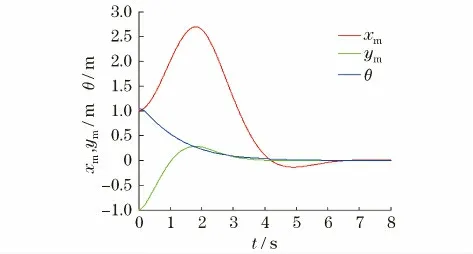
图3机器人状态变化曲线Fig.3 States of the robot with respect to time
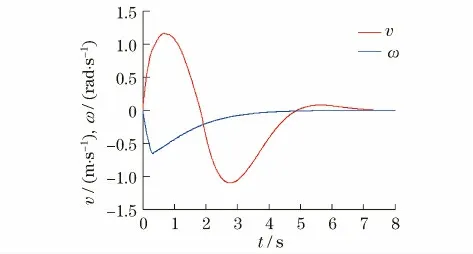
图4 机器人实际的速度变化轨迹Fig.4 Actual velocity with respect to time
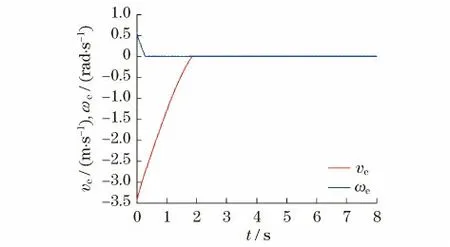
图5 速度误差变化曲线Fig.5 Velocity errors with respect to time
4 结论与展望
针对单目摄像机下的移动机器人,在摄像机参数未知以及带有不确定扰动的动力学的情况下,研究了其镇定问题.主要分为两步设计力矩控制器完成机器人的镇定.仿真结果有效地证实了理论的正确性.本文仅对θ0已知,而α1=a2未知的情况进行研究,未来将会放松这一假设条件.同时,滑模变结构控制的明显缺点就是抖振现象,如何有效地消除抖振也是未来努力的方向.
[1]Kolmanovsky I,McClamroch N H.Developments in nonholonomic control problems[J].IEEE Control Systems,1995,15(6):20-36.
[2]Wang G,Wang C L,Song X M,et al.Trajectory tracking of nonholonomic mobile robots via discretetime sliding mode controller based on uncalibrated visual servoing[M]∥Fei M R,Peng C,Su Z,et al.Computational Intelligence,Networked Systems and Their Applications.Berlin Heidelberg:Springer-Verlag,2014:342-350.
[3]Brockett R W.Asymptotic stability and feedback stabilization [J].Differntial Geometric Control Theory,1983,8:181-191.
[4]Yang J M,Kim J H.Sliding mode control for trajectory tracking of nonholonomic wheeled mobile robots[J].IEEE Transactions on Robotics and Automation,1999,15(3):578-587.
[5]Becerra H M,Lòpez-Nicolás G,Sagüés C.A slidingmode-control law for mobile robots based on epipolar visual servoing from three views [J].IEEE Transactions on Robotics,2011,27(1):175-183.
[6]Murray R M,Sastry S S.Nonholonomic motion planning:Steering using sinusoids[J].IEEE Transactions on Automatic Control,1993,38(5):700-716.
[7]Jiang Z P,Nijmeijer H.A recursive technique for tracking control of nonholonomic systems in chained form[J].IEEE Transactions on Automatic Control,1999,44(2):265-279.
[8]Astolfi A.Discontinuous control of nonholonomic systems[J].Systems &Control Letters,1996,27(1):37-45.
[9]Tian Y P,Li S H.Exponential stabilization of nonholonomic dynamic systems by smooth time-varying control[J].Automatica,2002,38(7):1139-1146.
[10]Chaumette F,Hutchinson S.Visual servo control,Part I:Basic approaches[J].IEEE Robotics and Automation Magazine,2006,13(4):82-90.
[11]Chaumette F,Hutchinson S.Visual servo control,Part II:Advanced approaches[J].IEEE Robotics and Automation Magazine,2007,14(1):109-118.
[12]Dixon W E,Dawson D M,Zergeroglu E,et al.Adaptive tracking control of a wheeled mobile robot via an uncalibrated camera system[J].IEEE Transactions on Systems,Man,and Cybernetics.Part B:Cybernetics,2001,31(3):341-352.
[13]Fang Y,Dixon W E,Dawson D M,et al.Homographybased visual servo regulation of mobile robots[J].IEEE Transactions on Systems,Man,and Cybernetics.Part B:Cybernetics,2005,35(5):1041-1050.
[14]Chen J,Dixon W E,Dawson M,et al.Homographybased visual servo tracking control of a wheeled mobile robot[J].IEEE Transactions on Robotics,2006,22(2):406-415.
[15]Mariottini G L,Oriolo G,Prattichizzo D.Image-based visual servoing for nonholonomic mobile robots using epipolar geometry[J].IEEE Transactions on Robotics,2007,23(1):87-100.
[16]Lopez-Nicolas G,Gans N R,Bhattacharya S,et al.Homography-based control scheme for mobile robots with nonholonomic and field-of-view constraints[J].IEEE Transactions on Systems,Man,and Cybernetics.Part B:Cybernetics,2010,40(4):1115-1127.
[17]Fang Y C,Liu X,Zhang X B.Adaptive active visual servoing of nonholonomic mobile robots[J].IEEE Transactions on Industrial Electronics,2012,59(1):486-497.
[18]彭飞,王朝立.基于车载摄像机移动机器人的模糊神经网络跟踪[J].上海理工大学学报,2014,36(4):385-390.
[19]Fukao T,Nakagawa H,Adachi N.Adaptive tracking control of a nonholonomic mobile robot[J].IEEE Transactions on Robotics and Automation,2000,16(5):609-615.
[20]马保离,霍伟.非完整链式系统的时变光滑指数镇定[J].自动化学报,2003,29(2):301-305.
[21]Fierro R,Lewis F L.Control of a nonholonomic mobile robot:backstepping kinematics into dynamics[C]∥Proceedings of the 34th IEEE Conference on Decision and Control.New Orleans,LA:IEEE,1995:3805-3810.
[22]Campion G,Bastin G,Dandrea-Novel B.Structural properties and classification of kinematic and dynamic models of wheeled mobile robots [J].IEEE Transactions on Robotics and Automation,1996,12(1):47-62.
[23]Lewis F L,Abdallah C T,Dawson D M.Control of robot manipulators [M].New York:Macmillan Publishing Company,1993.
[24]Bhat S P,Bernstein D S.Finite-time stability of continuous autonomous systems[J].SIAM Journal on Control and Optimization,2000,38(3):751-766.
[25]Dorf R C,Bishop R H.Modern control systems[M].New Jersey:Prentice Hall,2011.
[26]Slotine J J E,Li W P.Applied nonlinear control[M].New Jersey:Prentice Hall,1991.

