某转管武器后坐力静态标定装置的设计与分析

□ 牛碧凯 □ 王惠源 □ 赵良伟

1.中北大学 机电工程学院 太原 030051

2.中国兵器工业208所 北京 102200

某转管武器后坐力静态标定装置的设计与分析

□ 牛碧凯1□ 王惠源1□ 赵良伟2

1.中北大学 机电工程学院 太原 030051

2.中国兵器工业208所 北京 102200

针对某转管武器后坐力的标定，设计了一种后坐力静态标定装置，并对装置内部的关键部件推力杆分别利用欧拉公式和ANSYS软件对其进行理论求解和仿真分析，进行了稳定性校核。并将两者结果进行对比，证明了该构件设计的合理性和运用ANSYS软件进行数值模拟的可靠性。

后坐力标定 有限元分析 ANSYS 稳定分析

武装直升机发射武器时，武器的后坐力加入到原来的平衡系统中，直升机的运动状态将会发生变化。若这种变化十分剧烈，就会降低武器的射击精度，甚至引起飞行安全问题［1］。因此，在航空武器进行上机试验前，需要对武器的后坐力进行静态标定。针对某型号转管航空机枪后坐力标定，设计了一种加载装置对后坐力进行静态标定，并对装置中的关键部件进行了理论分析和有限元特征屈曲分析。

ANSYS是著名的有限元数值模拟软件，在工程计算中的应用非常广泛。屈曲分析主要用于研究结构在特定荷载作用下的稳定性以及确定结构失稳的临界载荷，屈曲分析包括线性特征值屈曲分析和非线性屈曲分析［2］。线性特征值屈曲分析是进行非线性屈曲分析的基础，线性特征值屈曲分析通常情况下可以为非线性屈曲分析提供合理的初始屈曲模态和与之对应的特征值。在非线性屈曲分析中，可以考虑结构初始缺陷、塑性行为、大变形响应等因素的影响，以更准确地模拟实际杆件的加载情况。

1 标定体系的组成

静态标定装置由立柱、推力丝杆、套筒、传感器座、推杆、推力杆等机构组成，装置的结构如图1所示。

工作时首先由人工转动力矩扳手带动推力丝杆运动，推力丝杆推动轴承座和压力传感器座向前直线运动，压力传感器测出传递力的大小并推动推杆向前运动，最后由装置前端的两个推力杆推动航枪的缓冲装置进行静态标定。

由于所标定的后坐力数值很大，并且装置中的传递力由推力杆传递给缓冲簧，因此要保证推力杆的同轴度，并且保证推力杆在工作过程中不能变形。在设计过程中必须要考虑推力杆能不能实现同轴且不会失稳，因此要对推力杆的材料和形状进行稳定性分析。该推力杆选用材料为45号钢，屈服极限σs=350 MPa；比例极限σp=280 MPa；弹性模量E=210 GPa；稳定安全因数nst=9。

▲图1 静态标定装置组成结构

▲图2 标定装置三维图

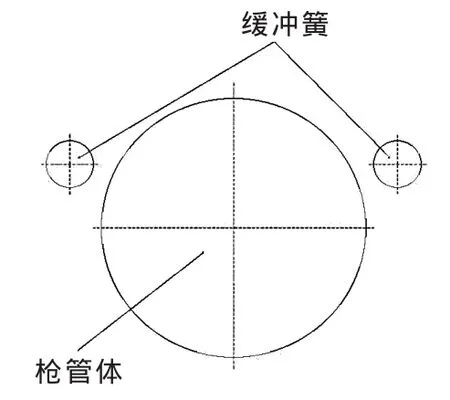
▲图3 航空机枪示意图

2 基于经典理论的计算

推力杆与连接块之间的配合是过盈配合，因此在分析中可以作出假设：①由于推力杆的直径相对于长度很小，可以把推力杆简化为一细长杆，假定推力杆为受压细长杆件；②推力杆与连接块配合处可以假设为推力杆底端固定、另一端自由受力；③ 假定从缓冲簧反作用于推力杆的力是在推力杆轴线上；④ 假定在计算中是等截面计算，取最危险的半径即凸台半径为推力杆稳定计算半径。

根据以上假设可以计算推力杆的临界压力：

式中：Fcr为推力杆的临界压力；E为弹性模量；I为横截面的惯性矩；μ为长度因数，取μ=2；l为推力杆长度。

与临界压力对应的应力为：

把式中横截面积的惯性矩I写成：

式中：i为截面的惯性半径。

这样，式（2）可以写成：

式中：λ=μl/i。

λ称为柔度或长细比，它集中地反应了推力杆的长度、约束条件、截面尺寸和形状等因素对临界应力σcr的影响［3］。

根据式（4），可以计算出极限值柔度为86，在本次理论计算中为等截面分析，可以取凸台直径大小作为计算直径，即20 mm，根据式（5）计算得出柔度值为140，该推力杆为大柔度推力杆。根据欧拉公式可以计算出临界压力Fcr=33 170.4 N。

3 有限元分析

3.1 模型建立及网格划分

建立正确的推力杆有限元模型是进行有限元分析的关键，在进行有限元分析时，主要分析推力杆在最危险截面的情况下满足稳定要求的情况，可以把推力杆看成细长杆进行有限元特征值屈曲分析。在进行单元选择时，选用BEAM189单元，BEAM189为计入剪切效应和大变形效应的3-D线性有限应变梁，适合于分析从细长到中等短粗梁结构。基于Timoshenko梁理论认为，在变形前，梁的横截面与梁的几何中心线是垂直的，而变形后，由于考虑了横向剪切，其横截面不再与几何中心面相垂直，而这个不垂直量即为横向剪切量，整个量的计算可以通过严格的推导得出［4］。对于不同梁有不同的剪切修正系数，计算结果接近实体模型。因此，选用BEAM189单元进行单元网格划分，建立的模型和划分网格如图4所示。

3.2 应力分析

引入合适的边界条件能提高计算精度，边界约束应该尽量与实际相符，避免出现过约束或欠约束［5］。本计算先在模型的底端施加固定位移约束，然后再施加载荷进行求解。求解完成后进入后处理模块，查看推力杆弹性体的相对应力分布和屈曲载荷系数，结果如图5所示。

由分析结果可以看出，显示的屈曲载荷系数为31 525.6，由于在静应力分析时给结构施加的是单位载荷，所以该推力杆的临界压力即为31 525.6 N，与理论分结果相比相对误差为4.9%。

4 结论

通过本研究可以得到以下结论。

▲图4 推力杆简化模型网格

▲图5 推力杆简化模型分析结果

（1）本文首先建立一种新型的后坐力静态标定装置结构，并对其中关键部件进行了理论分析和有限元特征值屈曲分析，证明了该结构设计的合理性和适用性。

（2）通过对推力杆弹性体进行ANSYS有限元屈曲分析，得到了杆件的相对应力分布和屈曲载荷系数，并和理论计算结果进行了对比，发现通过ANSYS计算得到的结果与欧拉公式计算结果相差较为吻合，证明了ANSYS计算结果在工程应用中的可参考性。

（3）通过本次分析计算，可以为以后该标定装置的改进和优化提供参考。

［1］向锦武，杨超.俯冲状态炮击后座力对直升机姿态的影响［J］.飞行力学，1999（3）：27-31.

［2］刘鸿文.材料力学［M］.北京：高等教育出版社，2004.

［3］张洪才.ANSYS14.0理论解析与工程应用实例［M］.北京：机械工业出版社，2012.

［4］何晶晶.压杆弹塑性失稳的ANSYS分析 ［J］.科苑杂谈，2007（22）：48-49.

［5］李丽君，沈玉凤.ANSYS对压杆稳定的辅助教学［J］.实验科学与技术，2009（2）：121-123.

［6］贺向东，张义民.薛玉春.等.压杆稳定可靠性优化设计［J］.中国工程科学，2007（9）：33-35.

（编辑 丁 罡）

TH123+.1；TJ302

A

1000-4998（2015）02-0061-03

2014年7月