浅谈"数形结合"思想在解题中的应用

邱元香

（三明市明溪县城关中学 福建三明 365000）

浅谈"数形结合"思想在解题中的应用

邱元香

（三明市明溪县城关中学 福建三明 365000）

数与形是和谐与统一的整体，是把抽象的数学语言与直观的图形结合，是数学教学和数学研究不可分割的两个方面。数形结合思想是数学教学中重要的解题思想。在教学中反复渗透数形结合的思想，使学生逐步学会运用数形结合的思想去分析问题，从而提高学生分析问题和综合解决问题的能力。

数形结合 解题应用

数与形是和谐的统一的整体，是数学教学和数学研究不可分割的两个方面。由图形性质来研究数量关系，或由数量关系来研究图形性质，这种重要的数形结合的数学思想方法，在我们初中数学教材中都有所渗透。在七年级“有理数”一章中就先入为主，充分利用数轴直观形象地表述了有理数的有关概念及运算。到方程解应用题中又通过列表、图式，使隐含的等量关系明朗化；而八年级，随着无理数的引入，运用数形结合的思想，学生对“数轴上的点与实数一一对应”就很容易理解；勾股定理及其逆定理的证明以及直角三角形相似的判定，无不体现数形结合的思想。

所以我们在教学中必须反复渗透数形结合的思想，让学生在不知不觉中不断强化、领会、掌握数形结合思想，这样才能让学生在解题时自觉运用，提高学生分析问题和解决问题的能力。

有很多数学问题，在使用常规方法进行证明或解答时，常常无从下手，若利用数形结合的方法去证明、解答，立竿见影，由繁变简，从而使问题迎刃而解。现本人结合自己多年初中数学教学活动中的体会，谈谈数形结合思想在解题中的应用。

一、利用数形结合巧解最值问题

新课标中注重数学知识应用于生活中，特别强调数形结合的思想在人们日常生活中的应用，同时可以发展学生的思维能力。

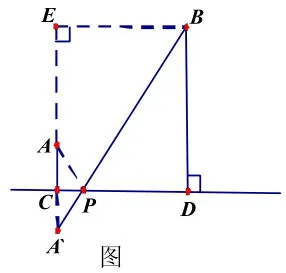
例1：如图（1），A、B两个村子在河CD的同侧，A、B两村到河CD的距离分别为AC=2千米，BD=10千米，且CD=5千米，现在要在河边 CD上建一自来水厂，分别向 A、B两村输送自来水，铺设水管工程费用为每千米 2万元，问：P在CD上的那个位置可以使铺设水管的费用最省？总费用多少？

解析：要使铺设水管的费用最小，即 PA+PB须最短，先作出点A 关于CD的对称点A′，根据两点之间线段最短，连接A′B 与直线 CD 的交点 P，即为所求，则 PA=PA′，那么PA+PB=PA′+PB=A′B，

问题转化为求 A′B，根据题意构造直角三角形，利用勾股定理可求A′B的长。

解：作 A 关于直线 CD的对称点 A′，连接 A′B，与 CD的交点，即为自来水厂P的位置，连接PA，则PA =PA′，过B作 BE⊥A A′交 CA 的延长线于 E，则 BE=CD=5千米，CE=BD=10千米， A′C=AC=2千米，

A′E=10+2=12千米，根据勾股定理，得：

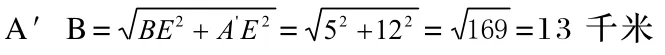
∴铺设水管的总费用为2×13=26万元。

∴蜘蛛爬行的最短路程为 10。

例 2、如图（2）所示，圆锥的母线长 OA=8，底面的半径 r=2，若一只小虫从点A出发，绕圆椎的侧面爬行一周后又回到点A，则小虫爬行的最短路线的长是多少？

解析：学生在解此题时，想当然地认为小虫爬行的最短路线就是圆锥底面圆的周长 π4。而实际上并非如此，我们必须将圆锥的侧面展开，沿母线 OA剪开，展开得一扇形，连接 AB，根据两点之间线段最短，从而求出最短路线的长。

设扇形的圆心角为n度，则：

以上两题，要学会把实际问题转化为数学问题，由形助数，把问题解决。

图

二、数形结合在代数式求解中的应用

在有理数的运算中，学习乘方运算时，一旦出现 n次方，比较抽象，学生较难理解，下面举例说明。

解析：这是初一练习册的一道题目，是高中的数列求和问题，对初中学生来说有一定的难度。

方法一：可设计如图所示的一个边长为 1的正方形，其面积为1。

让学生思考：连接正方形的一条对角线所得两个三角形的面积如何？再作其中一个三角形底边上的高所得的两个三角形的面积又如何？依此方法一直作下去呢？学生很容易就明白：

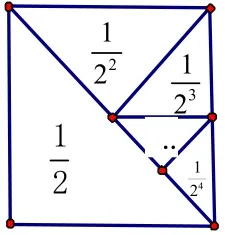
图

方法二：设计另一种情境：用一根长为1米的木棒，第一次先截去第二次再截去剩下的依次进行下去… …（如图4）

图（4）

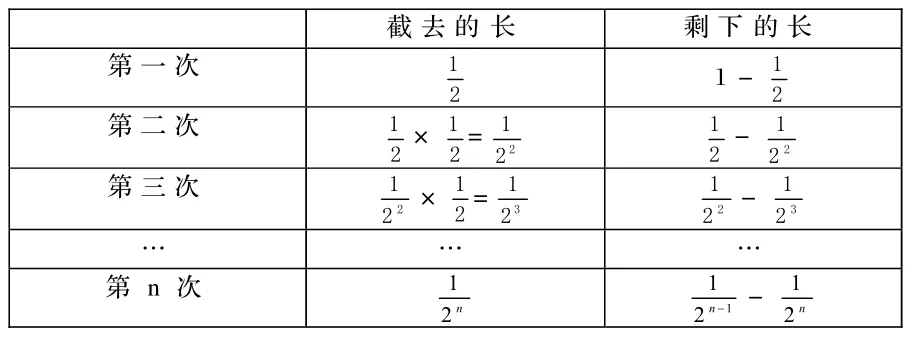
我们可以列表表示上述关系：每次截去的木棒长都等于剩下的木棒长。

于是

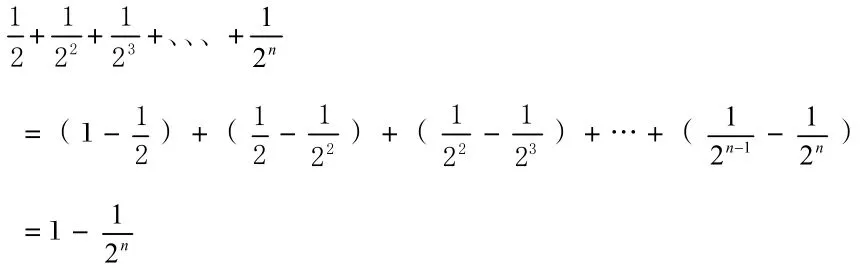
通过数与形的结合，把原本看过去不可解的数学计算问题，借助具体的图形，把原本抽象的数学问题形象化，学生既明白也容易理解。

三、利用数形结合巧解字母的取值范围

在不等式这一章中，有关于字母的取值范围是难点，学生常常出错，下面举例说明。

例4：关于a的不等式3x-a≤0的正整数解是1、2、3，求 a的取值范围。

由于不等式3x-a≤0的正整数解是1、2、3，

例5：已知方程关于x的方程 x2-（4a-1）x+3a+4=0的一个根大于5，另一个根小于5，求a的取值范围。

解析：本题如果直接解答，要考虑一元二次方程根的判别式及根与系数的关系，解起来比较麻烦，如果利用二次函数及图象联系起来，可直观简捷地解决问题。

令 y= x2-（4a-1）x+3a+4，则问题转化为抛物线y= x2-（4a-1）x+3a+4与 x轴的交点在（5、0）的两侧，因为 1＞0.抛物线的开口向上，画出草图，如图（5）所示：

图（5）

由图像可以知道当x=5时，y＜0，

即52-（4a-1）5+3a+4＜0解得a＞2，即为a的取值范围。

此题看似与图像无关，但却可以利用图像解决，因此利用数形结合，可以拓宽思路提高学生的分析能力。

四、数形结合在函数中的应用

在初中数学学习过程中，最难理解和掌握的就是函数了，函数是在某一变化过程中，出现两个变量，尤其是解析式中出现了待定系数时，增加了函

数的难度，因此学生要善于利用数形结合，对函数的图像和性质深入理解和掌握，掌握解题技巧，提高解题能力。

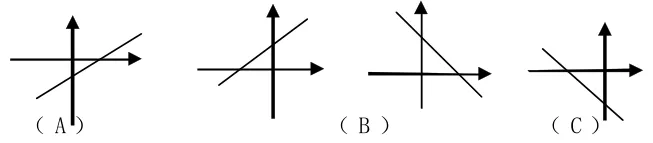
例 6：二次函数 y=ax2+bx+c的图像只经过第一、二、三象限，则一次函数y=ax-b的图像是（ ）

图

解析：此题未给出二次函数的图像，若凭空想象，大多数学生得不到正确的结论。因此我们必须画出二次函数的草图（如图 6）。结合图像，再结合二次函数的一些性质，就可以判断 a、b、c的取值范围，进而可以得出正确结论。

由图可知：抛物线开口向上，所以 a＞0，

抛物线与y轴交于正半轴（含原点），所以c≥0，

∴a，b同号，∴b＞0

∴一次函数y=ax-b的图像经过第一、二、四象限，应选A。

五、利用数形结合巧解几何求值题

有些几何问题若能以“数”助“形”，把复杂的几何问题转化成代数问题，能使问题简单化。

求∠C的度数

解析：由∠BAC-∠B=900，故设法构造直角三角形。

如图 8，在已知△ABC中，过 A 作 AD⊥AC，交 BC于 D，则∠DAC=900

∵∠DAC=∠BAC-∠BAD=900，

∵∠DAC=∠BAC-∠BAD=900，

又∠BAC-∠B=900

∴∠B=∠BAD，则BD=AD，

∴∠C=300

总之，在教学过程中，教师要反复渗透数形结合思想，在形的问题难以解决时发挥数的功能，在数的问题遇到困难时，画出与它相关的图形，使学生逐步学会运用数形结合的思想去分析问题，解决问题，养成良好的思维习惯，就能逐步培养学生的数学能力，提高学生的解题能力。

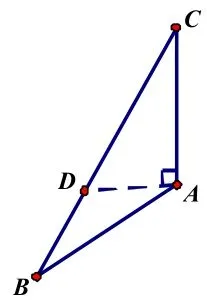
图（7）

2002.1 ～2中小学数学

1999.3 中学数学杂志