Maple软件在微分学教学中的应用探究

刘琼刘英迪

（1.邵阳学院理学与信息科学系 湖南邵阳 422000；2.湖南商学院财政金融学院 湖南长沙 410205）

Maple软件在微分学教学中的应用探究

刘琼1刘英迪2

（1.邵阳学院理学与信息科学系 湖南邵阳 422000；2.湖南商学院财政金融学院 湖南长沙 410205）

讨论了在一元函数微分学的教学中利用Maple数学软件计算复杂函数的导数、绘制函数图像和处理导数的应用问题，有益于提高学生学习数学的积极性和主动性以及运用数学知识解决实际问题的能力.

微分学 Maple软件 作图

引言

微分学的基本概念是导数，导数有着深刻的实际背景，它反映了函数相对于自变量的变化快慢程度，是研究分析函数的重要工具和方法之一，是高等数学的重要组成部分，导数作为一个数学工具无论在理论上还是实际应用中，均起着基础而重要的作用。Maple是世界上享有盛誉的数学软件之一，具有非常强大的数值和符号计算功能、灵活多变的绘图及动画制作技术，它的应用已经涉及到数学物理、经济和工程技术等领域，其提供的 Student软件包是大学生学习高等数学的好助手，本文就Maple软件在一元函数微分学教学中的应用进行一些探讨。

1.计算复杂函数的导数

我们在高等数学教材和一些数学参考书上找到一些复杂函数的求导题，这些题用手工方法求导比较繁杂，我们可以借助Maple软件来解决这一问题。

解：在Maple工作窗口输入：

由此得：

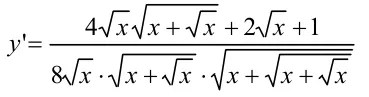
解：在Maple工作窗口输入：

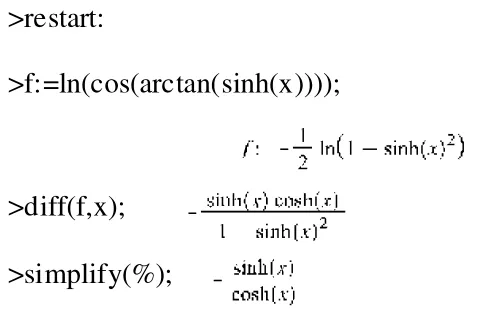
2.绘制函数图像

对于Maple软件而言，一般情况只要输入函数表达式，在作图命令下会很快绘制出函数图像，但这样绘制的图像其极值点、拐点和渐近线等信息不充分，另

一方面，若函数中有方根项时，一般 Maple软件只绘出方根中大于零的一段，从而使绘出的图像不完整，为此我们按照教材中函数作图的步骤，利用Maple软件来对函数作图。

解：该题若输入函数表达式，在作图命令作用下，我们发现只作出函数在内的图像。

在Maple工作窗口输入：

综上所述，函数的性态如下表：

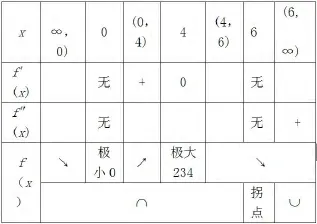
且易得曲线有斜渐近线：y=-x+2

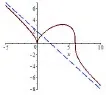
图1

3 处理导数的应用问题

【例题3.1】求函数 |2| xsimxy += 在 ），0（π内的单调区间和极值.

解： 在Maple工作窗口输入：

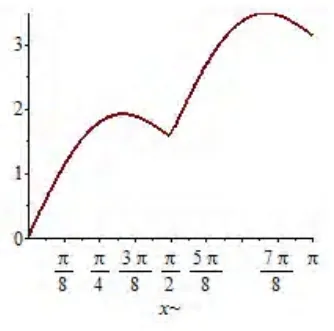
图2

用Maple作图验证（图2）：

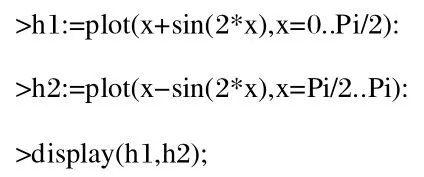
解：在Maple工作窗口输入：

4 结束语

以上是我们对在一元函数微分学的教学中利用 Maple数学软件解决一些问题的举例讨论，其实它的应用不仅仅只局限于上述几个方面，本文只是抛砖引玉在高等数学教学中充分利用数学软件，可解决学生为之头痛的繁复计算问题，能够动态地演示空间几何图形和各种变量之间的关系，帮助学生分析和理解问题，从而提高学生学习数学的积极性和主动性，为学生后续专业课程的学习打下坚实的数学基础，同时又促使学生更好地学习 Maple软件，增强他们利用这一工具解决实际问题的能力。

［1］黄立宏.高等数学（第三版）［M］.复旦大学出版社，2013.

［2］周民强.高等数学学习辅导［M］.北京邮电大学出版社，2010.

［3］何青，王丽芬.Maple教程［M］，北京：科学出版社，2006.

［4］张韵华，王新茂.符号计算系统Maple教程［M］，合肥：中国科学技术大学出版社，2007.

［5］刘琼.Maple软件在复变函数中的应用［J］，邵阳学院学报，2013，10（1）：20-25.

［6］刘琼，刘英迪.Maple数学软件与Laplace积分变换 ［J］.邵阳学院学报，2014，11（2）：14-18.

刘琼（1964-），男，汉族，湖南邵阳人，副教授，从事解析不等式和数学教育理论的研究。

［项目来源：（1）湖南省普通高等学校教学改革研究立项项目"基于应用型人才培养的《高等数学》课程教学改革探究"（湘教通［2014］247号，No：448）；（2）湖南省教育科学"十二五"规划立项课题"创新教育视阀下地主高校数学实验课程建设和实践的研究"（No：XJK014CGD078）］