滚珠丝杠冷滚打的齿形理论误差研究

李玉玺，李言，杨明顺，崔凤奎，何选景

（1.西安理工大学机械与精密仪器工程学院，陕西西安710048；2.河南科技大学机电工程学院，河南洛阳471003）

滚珠丝杠冷滚打的齿形理论误差研究

李玉玺1，李言1，杨明顺1，崔凤奎2，何选景2

（1.西安理工大学机械与精密仪器工程学院，陕西西安710048；2.河南科技大学机电工程学院，河南洛阳471003）

丝杠冷滚打加工打破了传统的材料"去除"式加工方法存在的局限，具有高效，节能、节材及产品耐磨性好、使用寿命长等优点。依据微分几何和啮合原理，建立了滚珠丝杠冷滚打过程中齿面啮合模型和理论误差模型，给出了啮合面的接触线函数，揭示了滚珠丝杠冷滚打过程中滚打轮和工件的相对运动关系，为滚打轮的正确设计奠定了基础。通过理论计算与仿真分析，对滚珠丝杠冷滚打的齿形误差和滚珠中心轨迹螺旋线误差进行研究，分析了误差产生的原因并给出了相应的解决方法。利用自行设计的滚打装置进行丝杠冷滚打试验，试验得到的实际加工轮廓线和理论接触线基本重合，对丝杠冷滚打精确成形提供了参考依据。

机械制造工艺与设备；滚珠丝杠；冷滚打；啮合原理；理论误差

0 引言

滚珠丝杠副具有传动效率高、传动精度高、运动平稳性好及使用寿命长等优点，在航天、航空、核工业、工程机械、车辆装备等领域应用极其广泛［1-3］。滚珠丝杠作为滚珠丝杠副传动的关键部件，在很大程度上决定滚珠丝杠副的运转特性。大部分滚珠丝杠的螺旋滚道的法向截面形状采用两条圆弧拼接而成［4］。滚珠丝杠的一般加工工艺是先铣削最后磨削，其具有生产效率低、制造周期长、材料利用率低及金属表面组织被切断等缺点，从而降低了滚珠丝杠的力学性能［5-6］。目前先进的加工方法有旋风铣削和滚压。旋风铣削最大的特点是加工效率高，缺点是金属纤维容易被切断，且材料利用率低。滚压属于无屑加工，缺点是对滚压头的刚度要求非常高以及滚压轮制造困难且成本较高［7］。因而，研究和开发滚珠丝杠新的加工方法是非常必要的。

冷滚打加工是应用塑性成形技术替代传统的切削加工方法，打破材料“去除”加工原理，实现“累积”成形，有加工效率高、节省材料、热处理变形小、产品耐磨性好及使用寿命长等优点。目前，高速冷滚打加工技术在齿轮、花键轴等轴类产品的加工上已经得到了应用［8-10］。李言等进行了丝杠冷滚打的动力学仿真和成形过程的有限元仿真分析，开展了初步的可行性实验，对丝杠冷滚打成形过程中的金属流动规律进行了初步研究［11-12］。本文基于啮合原理和滚珠丝杠螺旋面理论法向截面形状，建立冷滚打运动关系模型、齿形啮合函数以及滚珠丝杠理论误差模型，以期进一步探讨丝杠冷滚打的成形原理，提高冷滚打制件的成形精度，最后通过试验验证加工方法的可行性。

1 滚珠丝杠冷滚打加工基本原理

1.1 滚珠丝杠冷滚打运动分析

冷滚打滚珠丝杠成形所需要的最主要的运动是滚打轮与滚珠丝杠二者之间的相对运动，也就是滚打轮与滚珠丝杠之间的相对运动方向和滚珠丝杠螺旋槽的切线方向同向。在对滚打轮进行安装时，滚打轮的轴线与滚珠丝杠的轴线之间的空间夹角与滚珠丝杠的螺旋升角β相等（如图1）。冷滚打成形过程中，丝杠轴坯绕其轴线做有规律的旋转运动。滚打轮绕其公转中心旋转，同时由于滚打轮和滚珠丝杠接触时会产生一定的摩擦力，因此滚打轮还会产生自转。此外，滚打轮还会沿滚珠丝杠轴线方向按照特定的进给速度做直线运动。这样就逐渐冷滚打出了整个滚珠丝杠螺旋面。

1.2 滚珠丝杠冷滚打坐标系及几何模型

依据丝杠冷滚打加工原理建立的滚打轮和工件冷滚打运动的右手笛卡尔坐标系如图2所示。S0为空间固定坐标系，其中k0轴与工件回转轴重合，方向为工件的进给方向；Su为空间辅助固定坐标系，其中ku轴与工件的回转轴相垂直且相距L（即滚打轮公转中心与花键的中心距）；Sq为冷滚打轮固连参考坐标系；Sr（δ）为滚打轮固连动坐标系，其坐标原点or，与oq重合，jr轴和jq轴的夹角为滚打轮的自转角θ；Sg（α）为刀架固连坐标系；S1（φ）为工件固连动坐标系；Sa为随刀架移动坐标系，其原点oa与oo重合，ka轴与ko轴一致；β为丝杠的螺旋升角；α为滚打轮的公转回转角；φ是工件的旋转角度；ωr是滚打轮自转的角速度矢量。

图1 滚打轮与滚珠丝杠位置图Fig.1 Position of roller and ballscrew

图2 冷滚打运动关系坐标系Fig.2 Moving coordinate system of coll rolling

滚打轮的回转面是由滚打轮轴向截线绕其中心旋转一周而形成的。为了研究冷滚打滚珠丝杠成形原理，此时滚打轮轴向截线设计最容易实现的就是使其轴向截线和滚珠丝杠螺旋面法向截线保持一致。如图3所示，此处滚珠丝杠法向截线为双圆弧，根据几何关系即可得到滚打轮回转面的方程。（1）式为求得的滚打轮右侧回转面方程。

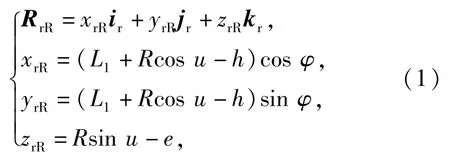
式中：L1为滚打轮中心or距离om（Sm为沿滚珠中心的活动标架）点的最短距离，L1=L-L2-h，L2为滚打轮公转中心到其自传中心的距离，L为滚打轮公转中心与滚珠丝杠轴线的垂直距离；φ为滚珠丝杠轴向截线绕zr轴旋转角；e为圆弧滚道偏心距；h为圆弧滚道位置参数；R为圆弧滚道半径；u为圆弧轴向截型角参变数。

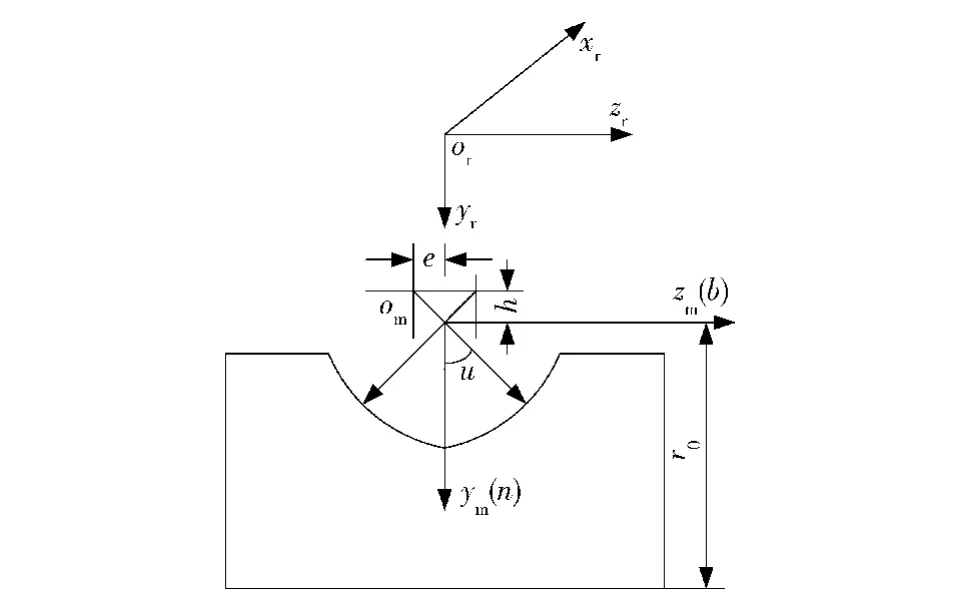
图3 滚打轮齿面成形原理图Fig.3 Schematic diagram of tooth forming of roller

根据微分几何知识可知，滚打轮曲面上任意点的单位法向量n为

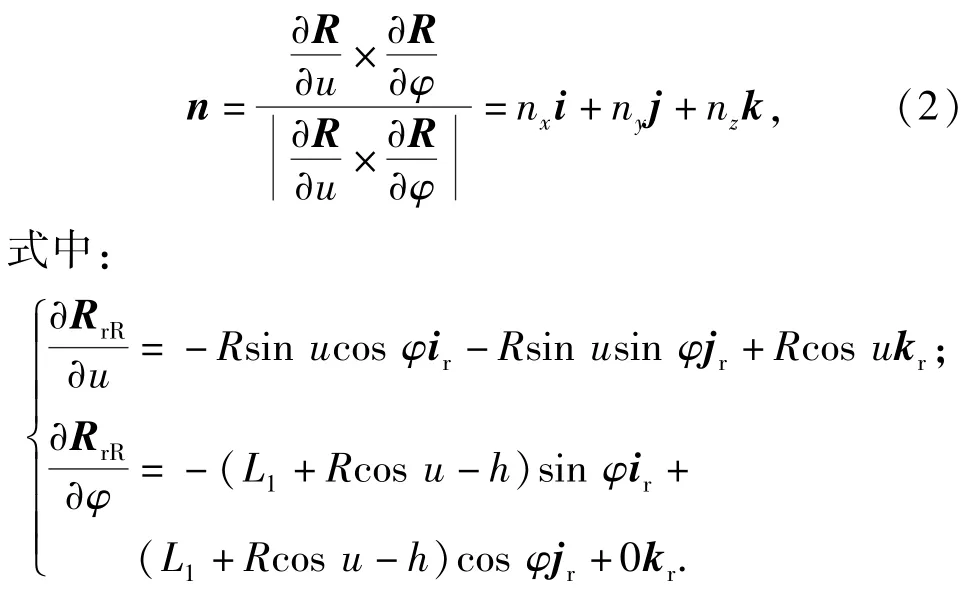
将参数代入（2）式计算出联立求解可得滚打轮右侧单位法向量为

求出滚打轮与滚珠丝杠的相对速度，是运用啮合原理求取啮合方程的关键。图4所示为冷滚打运动关系的矢量图，根据滚动矢量关系可求得任意接触点的速度与位置的关系。

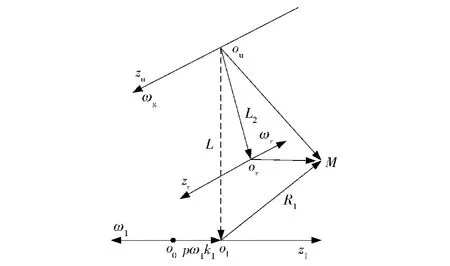
图4 冷滚打运动关系矢量图Fig.4 Vector diagram of moving relation of coll rolling

在Su坐标系中，滚轮上任意点M的速度vr等应该是牵连速度（公转速度）vg和相对速度（自转速度）vrg的合成，即

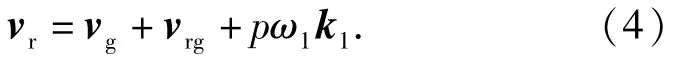
M点在滚珠丝杠上的速度为

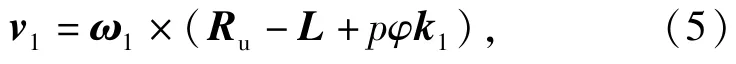
式中：

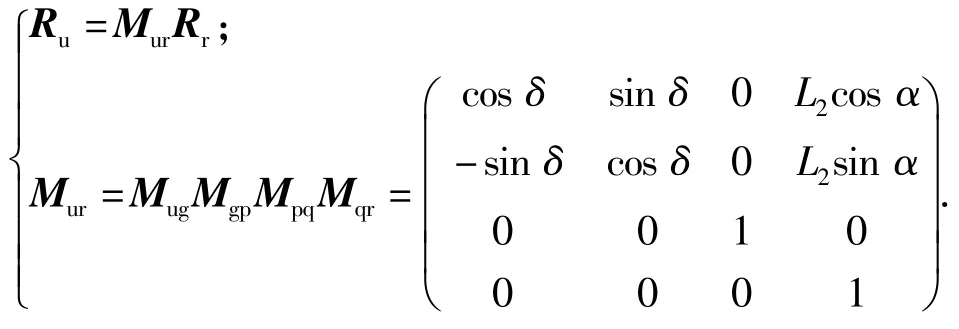
在坐标系Su中，M点的相对速度为

将（4）式和（5）式代入（6）式可得

根据啮合原理，经过推导、整理可得在S1（φ）坐标系中，滚珠丝杠右侧齿槽齿面方程如下：

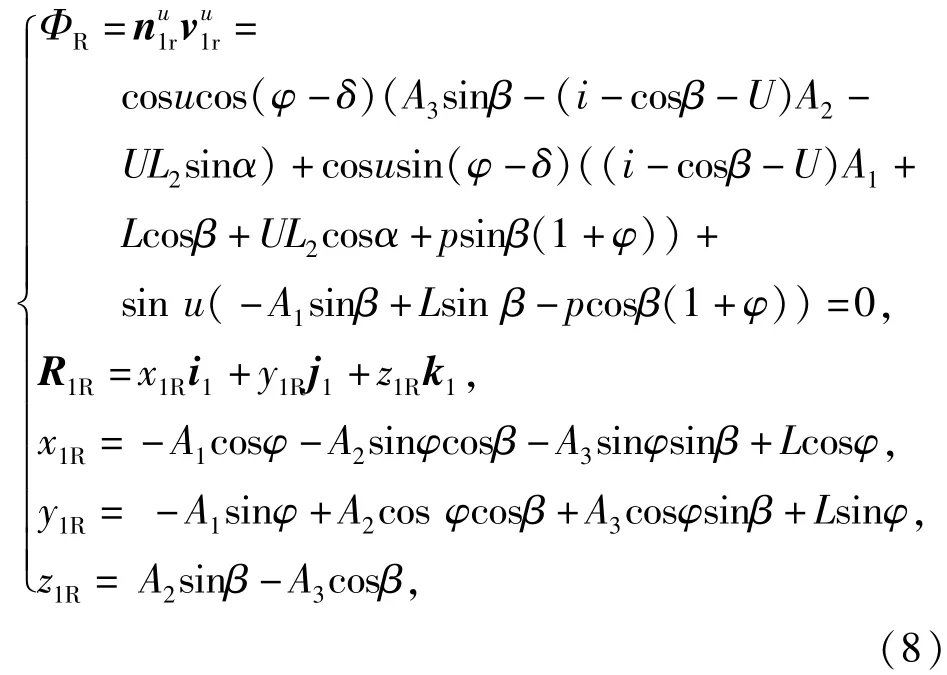
式中：ΦR=0为滚珠丝杠右侧啮合方程；；U=，rd为滚打轮半径。

2 冷滚打成形原理分析

以某型号滚珠丝杠为例，其双圆弧法向截面形状参数及相关工艺参数如表1所示。滚打轮半径rd=19 mm；滚打轮公转中心到其自传中心的距离L2=36 mm；滚打轮的公转角速度ωg=2 000 r/min；滚打轮公转角速度与滚珠丝杠旋转角速度之i= 400.

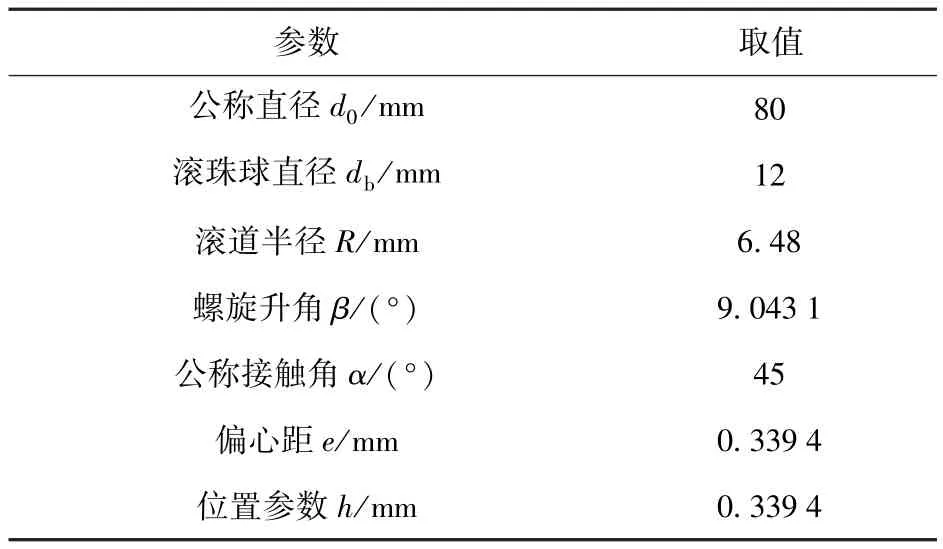
表1 滚珠丝杠形状及工艺参数Tab.1 Shape and processing parameters of ballscrew

由（8）式计算可以得出，滚打轮公转一周所得到的滚珠丝杠的产形面主视图、俯视图及滚珠丝杠齿槽右侧啮合面分别如图5～图7所示，实际接触线与理论法向截线在S1坐标系中的o1x1y1平面的投影分别如图8和图9所示。

图5 滚珠丝杠产形面俯视图Fig.5 Top view of generating surface of ballscrew

2.1 滚珠丝杠成形原理的宏观分析

由图5可以看出，齿槽左右两侧的曲面都是向右偏，也就是说滚珠丝杠沿自身轴线的旋转速度与滚打轮的轴向进给速度存在一定的比例关系，丝杠轴坯相对于滚打轮做的是螺旋运动，滚珠丝杠的成形面是由这种螺旋运动产生的有限个螺旋面沿工件轴向方向包络而成。从图5还可以看出，接触线在左右两侧边缘处所构成的是两个圆弧，这两个圆弧是滚打轮切入圆形毛坯中所形成的边缘点在o1y1z1面投影得到的；上下两侧则是两条直线，这两条直线同样也是滚打轮左右两侧与切入圆形毛坯中在边缘处所构成的两条曲线在o1y1z1面投影所得到的。

图6 滚珠丝杠产形面主视图Fig.6 Front view of generating surface of ballscrew

图7 齿槽右侧啮合面Fig.7 Meshing surface on the right side of tooth groove

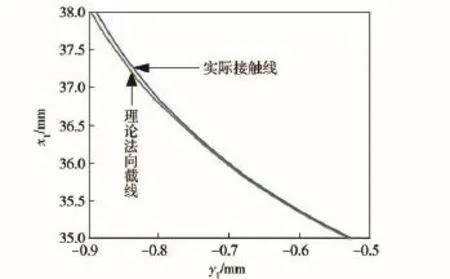
图8 α=0°时右侧接触线与法向截线Fig.8 Contact line and normal section line on right side for α=0°

由图6可以看出，滚打轮绕公转轴每旋转一周，在工件表面形成一个近似平滑齿槽，说明冷滚打是不断往复、逐渐累积的成形过程。齿槽左右两侧所对应的啮合线是不对称的，说明成形过程的运动不属于成形运动。形成齿槽两侧隆起的边缘点从上到下距离z1越来越远，主要是由于随着滚打轮打入深度的增加，成形的轮廓也随之扩大。

图9 α=0°时左侧接触线与法向截线Fig.9 Contact line and normal section line on left side for α=0°

2.2 滚珠丝杠成形原理微观分析

滚打轮对滚珠丝杠的滚打过程是一个连续的创成过程，分析滚打过程中的接触点，将α值相同下不同u值的接触点构成接触线，若干有限的接触线又组成了包络面，而整个齿形就是由这些包络面决定的。在实际过程中，由于滚打轮和滚打轨迹的有限性，导致滚珠丝杠齿面包络也具有有限性，使每个包络面都处于离散状态。在接触线上距离y1轴最近和最远的两个点分别是滚珠丝杠大径和小径与滚打轮的接触点。分析图8和图9可以得出：在S1坐标系中，理论上的法向截线与实际过程中的接触线并不重合，而且实际过程中，接触线往往比理论法向截线要小，由此可以说明滚打轮对滚珠丝杠的滚打是一个展成运动。

从滚珠丝杠齿廓的成形运动分析，滚珠丝杠齿槽曲面正是由若干个这样的啮合面沿着z1正向（滚珠丝杠轴向）包络而成，所以滚珠丝杠齿形的发生线（母线）是由沿z1方向距离x1轴的所有最远点所组成的，如图7所示。分析发现这些点是由若干的瞬时接触线包络而成，并非在同一条瞬时接触线上，由此可以得到冷滚打丝杠母线的成形方法为范成法。滚珠丝杠的转动、滚打轮的自转及公转决定了母线的形成。由于滚珠丝杠齿面是由啮合面沿滚珠丝杠轴向包络而成，所以滚打轮沿滚珠丝杠轴线的直线是冷滚打滚珠丝杠的导线。

3 误差分析

评价滚珠丝杠精度的指标主要有：导程、齿形误差以及表面粗糙度等，而其中滚道齿形和导程精度是最为重要的两项指标。滚珠丝杠螺旋滚道的齿形误差比较大的时候将导致滚珠丝杠副全长上接触状况的改变，因而加剧丝杠磨损，降低其传动精度。滚珠丝杠可以将角位移转换成线位移，并且满足了角位移和线位移之间的关系为一常数的要求，这些都需要通过滚珠丝杠精确地导程精度来保证。在开环或者半闭环系统中，高精度导程显得尤为重要。

3.1 齿形误差

滚珠丝杠齿形误差指的是在螺旋滚道法向截形上的实际齿形轮廓和理论齿形轮廓这二者之间的法向距离。滚珠丝杠右侧理论齿面方程为

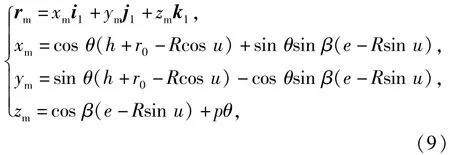
式中：r0为公称半径；θ为滚珠相对于滚珠丝杠的旋转角度。

经过误差计算得出齿槽右侧和左侧齿形误差ΔfR、ΔfL，如图10、图11所示。从计算结果来看，右侧最大误差为0.008 9 mm，齿顶误差为0.003 2 mm，齿底误差为0.008 9 mm，误差从齿顶到齿底逐渐增大。左侧和右侧的最大误差、齿顶、齿底的误差都一致，误差也是从齿顶到齿底逐渐增大。误差存在进一步证明了是由滚打轮成形法设计造成的。

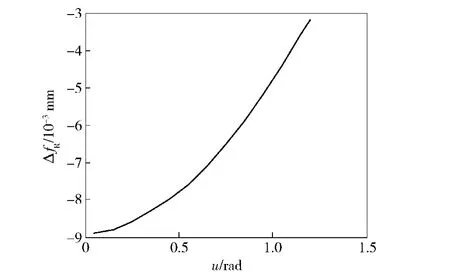
图10 齿槽右侧齿形误差Fig.10 Tooth profile error on the right side of tooth groove

3.2 滚珠中心轨迹螺旋线误差

冷滚打加工时，由于滚打轮与滚珠丝杠不是连续接触的，导致实际加工出的螺旋滚道不是理想螺旋面，因此实际滚珠中心轨迹螺旋线不是理想螺旋线。滚珠丝杠主要几何尺寸和滚珠中心轨迹螺旋线的误差如图12和图13所示，因为在同一螺旋线上任意一点到工件轴线的距离是相等的，滚打轮每次滚打过的微小弧长lp可以近似为微直线段，实际滚珠中心轨迹螺旋线与理论滚珠中心轨迹螺旋线的最大误差为Δl.

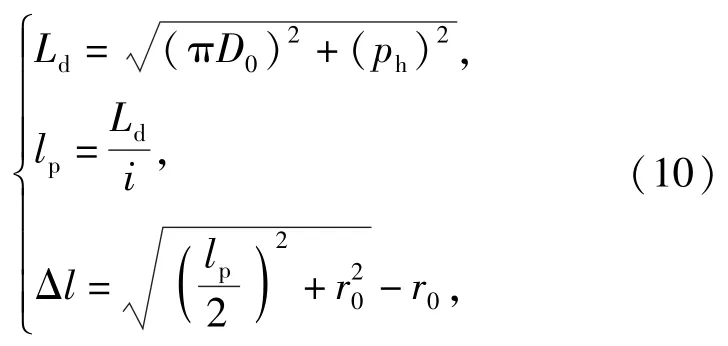
式中：Ld为理论滚珠中心轨迹转过一周的长度；D0为滚珠丝杠的公称直径；p为滚珠丝杠螺旋参数；ph为刀架移动距离。

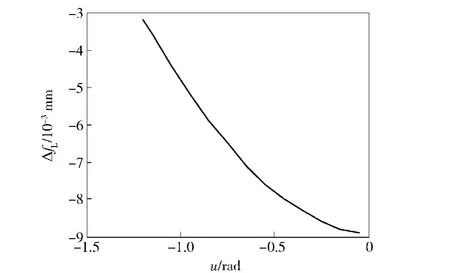
图11 齿槽左侧齿形误差Fig.11 Tooth profile error on the left side of tooth groove

图12 滚珠丝杠主要几何尺寸Fig.12 Main geometric dimensions of ballscrew

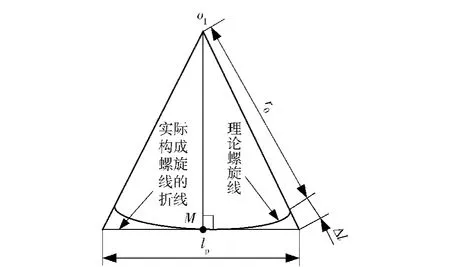
图13 滚珠中心轨迹螺旋线误差示意图Fig.13 Helical line error of ball at center track

将上面已知滚珠丝杠的参数代入（10）式进行计算，可得最大误差值为0.004 97 mm.从（10）式以及图13可以得出，造成误差的主要原因是在高速滚打过程中滚打轮与滚珠丝杠不是连续接触，在滚珠丝杠按照特定的速度转动一周的过程中，传动比如果增大就可以增加滚打轮对丝杠的滚打次数，并且减小了实际滚珠中心轨迹螺旋线的误差。

4 试验验证

丝杠冷滚打加工试验是通过改装后的CA6140机床进行的，试验采用的滚打轮材料为4Cr5MoSiV1，经调质处理后，将3个滚打轮均布在一个圆形刀盘上，滚打轮的转速为2 000 r/min，试件采用紫铜棒。冷滚打装置包括电机、履带以及刀盘；工作时通过电机带动滚打轮转动，滚打轮在与试件接触时由于摩擦力的作用可以自转。同时，滚打轮在刀架上按照预先设定好的速度进行直线移动。紫铜棒通过三抓卡盘和顶尖进行安装定位，同时三抓卡盘旋转带动试件转动。为了方便调整安装角，将该滚打装置安装在有分度功能的刀架上，同时冷滚打过程中为了降低滚打摩擦系数而采用润滑油。图14为冷滚打试验装置，图15为试验获得的加工试件的一部分。

图14 试验装置图Fig.14 Experimental setup

图15 试验加工的试件Fig.15 Processed test piece

将该滚珠丝杠沿着截面法向方向进行切割，切割后形状如图16所示，将切割后的试件放置在莱卡白光干涉仪的工作台上，计算机控制工作台的移动，使用基恩士LK-G10激光位移传感器测头对试件进行数据采集，将扫描数据进行拟合并截取其轮廓曲线，将得到轮廓线和理论计算的实际接触线进行对比，如图17所示，不难发现二者基本重合，充分说明丝杠冷滚打加工技术的可行性。

图16 试件Fig.16 Test piece

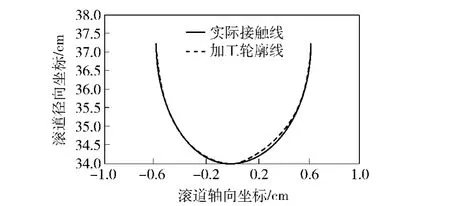
图17 廓形比较图Fig.17 Profile comparison

5 结论

本文基于微分几何和啮合原理，建立了冷滚打滚珠丝杠数学模型，导出了滚珠丝杠的齿面方程。并以某一型号的滚珠丝杠为例对滚珠丝杠成形原理进行了分析，结果表明，滚珠丝杠冷滚打是一种基于范成运动关系的成形过程。同时，给出了滚珠丝杠理论齿形误差和滚珠中心轨迹螺旋线误差的计算方法，并对其进行实例分析，得出了误差变化规律。初步得出了滚珠丝杠齿形误差是由滚打轮设计造成的，以及实际滚珠中心螺旋线误差是由滚打轮与滚珠丝杠接触不连续造成的结论。通过试验得知实际加工的轮廓和理论接触线基本重合，说明成形原理及误差分析的正确性。

（

）

［1］肖正义.滚珠丝杠副的发展趋势［J］.制造技术与机床，2000（4）：11-13. XIAO Zheng-yi.Development of ball screw［J］.Manufacturing Technology&Machine Tool，2000（4）：11-13.（in Chinese）

［2］Guevarra D S，Kyusojin A，Isobe H，et al.Development of a new lapping method for high precision ball screw（1st report）-feasibility study of a prototyped lapping tool for automatic lapping process［J］.Precision Engineering，2001，25（1）：63-69.

［3］Mei X S，Tsutsumi M，Tao T，et al.Study on the load distribution of ball screws with errors［J］.Mechanism and Machine Theory，2003，38（11）：1257-1269.

［4］Liu J Y，Hsu M H，Chen F C.On the design of rotating speedfunctions to improve the acceleration peak value of ball-screw transmission mechanism［J］.Mechanism and Machine Theory，2001，36（9）：1035-1049.

［5］崔凤奎，谢亚飞，董晓丹，等.高速冷滚打成形金属流动仿真分析［J］.河南理工大学学报，2014，33（4）：467-471. CUI Feng-kui，XIE Ya-fei，DONG Xiao-dan，et al.Simulation analysis of metal low in high-speed cold roll-beating［J］.Journal of Henan University of Technology，2014，33（4）：467-471.（in Chinese）

［6］Harada H，Kagiwada T.Grinding of high-lead and gothic-arc profile ball-nuts with free quill-inclination［J］.Precision Engineering，2004，28：143-151.

［7］Kimura Y，Fujita N，Matsubara Y，et al.High-speed rolling by hybrid-lubrication system in tandem cold rolling mills［J］.Journal of Materials Processing Technology，2014，216：357-368.

［8］崔凤奎.渐开线花键加工方法进展［J］.矿山机械，2007，35（2）：116-119. CUI Feng-kui.Processing method of module involute spline Sshafts［J］.Mining&Processing Equipment，2007，35（2）：116-119.（in Chinese）

［9］杨明顺，李言，袁启龙，等.板料冷滚打成形鳞纹影响因素解析及试验研究［J］.机械科学与技术，2013，32（9）：1363-1367. YANG Ming-shun，LI Yan，YUAN Qi-long，et al.Theoretical analysis and experimental study on stripe of slab cold roll-beating［J］. Mechanical Science and Technology for Aerospace Engineering. 2013，32（9）：1363-1367.（in Chinese）

［10］Lv J L，Luo H Y.The effects of cold rolling temperature on corrosion resistance of pure iron［J］.Applied Surface Science，2014，317：125-130.

［11］李言，杨明顺，李玢，等.丝杠冷滚打成形动力学仿真及分析［J］.西安理工大学学报，2009，25（4）：383-387. LI Yan，YANG Ming-shun，LI Bin，et al.Dynamics simulation and analysis of lead screw cold roll-beating［J］.Journal of Xi'an University of Technology，2009，25（4）：383-387.（in Chinese）

［12］张璐，李言，杨明顺，等.丝杠冷滚打成形过程金属流动规律研究［J］.中国机械工程，2012，23（13）：1623-1628. ZHANG Lu，LI Yan，YANG Ming-shun，et al.Study on metal flowing of lead screw cold roll-beating forming［J］.China Mechanical Engineering，2012，23（13）：1623-1628.（in Chinese）

Investigation of the Tooth Profile Error Based on the Forming Theory of Balloscrew Manufactured by Cold Rolling

LI Yu-xi1，LI Yan1，YANG Ming-shun1，CUI Feng-kui2，HE Xuan-jing2
（1.School of Mechanical and Precision Instrument Engineering，Xi'an University of Technology，Xi'an 710048，Shaanxi，China；2.School of Mechatronics Engineering，Henan University of Science and Technology，Luoyang 471003，Henan，China）

The traditional material removal machining method of ballscrews was broken by cold roll-beating.The cold roll-beating method has the advantages of high efficiency，energy conservation and saving in material.The products processed by the proposed method have high wear resistance and long service life.According to differential geometry and meshing theory，the meshing model and theoretical error model are constructed for the cold roll-beating of ballscrews，and the function of contact line is provided for meshing surface.The relative movement between roller and workpiece is revealed by analyzing the meshing model and the contact line.The profile errors of the gear tooth and the actual helix of the center track of ball are investigated by theoretical calculation and simulation，the causes of errors are analyzed，and the corresponding solutions are given.A self-developed cold roll-beating experimental device is used for cold roll-beating experiment of lead screws.The experimental results show that the actual machining contour line overlaps with the theoretical contact line.

manufacturing technology and equipment；ballscrew；cold roll-beating；meshing theory；theoretical error

TG66

A

1000-1093（2015）08-1594-07

10.3969/j.issn.1000-1093.2015.08.031

2014-12-07

国家自然科学基金项目（51475146、51475366）；陕西省教育厅重点实验室科学研究计划项目（12JS072）；西安理工大学博士创新基金项目（207-002j1302）

李玉玺（1984—），男，博士研究生。E-mail：lyx841125@126.com；李言（1960—），男，教授，博士生导师。E-mail：Jyxy-ly@xaut.edu.cn