基于遗传BP神经网络的隐身涂层老化性能评价模型
卢言利,穆景阳
(总装备部工程兵科研一所,江苏无锡214035)
基于遗传BP神经网络的隐身涂层老化性能评价模型
卢言利,穆景阳
(总装备部工程兵科研一所,江苏无锡214035)
为了计算涂层在自然环境中老化物理量值与环境因子的关系,设计出一种实数编码、算术交叉、高斯变异、爬山操作的遗传BP神经网络。根据环境因子计算涂层物理量值,采用Visual studio 2008进行编程,开发出程序进行神经网络训练和预测程序。用一个涂层野外老化数据的实例来进行网络训练和预测,结果表明,模型计算出涂层最终的寿命,与实际测量值相近,表明遗传神经网络模型可以很好地用于涂层寿命预测。
兵器科学与技术;隐身涂层;耐老化性能;BP人工神经网络;遗传算法;寿命预测
0 引言
隐身涂料作为一种重要的隐身材料而广泛应用于武器装备、军事工程的表面,起到了重要的隐身效果。涂料在加工、贮存和使用过程中,由于受内外因素的综合作用,其使用性能逐渐变坏,以致最后丧失使用价值,这种现象称为“老化”。涂层老化本质上是组分中的高聚物、颜料等在自然界中发生化学变化的结果,是材料的自然特性,也是一种不可逆变化,涂层的耐老化性能是涂料性能好坏的重要标志之一[1]。涂层的老化过程受很多因素影响,包括涂层自身化学材料、制作工艺和各种复杂自然条件,在自然界中涂层老化主要有热降解、水降解、光降解和氧化降解[2]。文献[3-6]对涂层老化机理进行了研究,老化降解主要是光引发的氧化和水解,其影响因素主要有阳光(特别是紫外线)、温度、氧气、水和污染物等。已有研究表明,光氧化降解随温度增大而加剧;同样水解降解也因光照而加剧[2]。
在涂料的研制和试验研究中,对其老化性能研究通常采用两类方法:一类是典型或严酷的自然环境老化试验,如大气老化试验;另一类是在实验室用仪器设备(即人工加速老化)来模拟特定的环境条件,并强化某些因素,在短期内获得试验结果,主要有针对太阳辐射、温度、湿度等来进行设计试验方法。但是上述两种方法在获取试验数据和验证涂层性能,同样存在试验周期长、效率低等问题。涂层老化的物理量值与自然界环境因子关系复杂,而且隐身涂料有其固有特征,老化评价指标与其他涂料有所不同,研究表明隐身涂层的颜色特征变化(主要为光泽值(保光率)与变色(色差),这两个参数是可以量化检测)对其隐身效果影响最大,影响其颜色特征变化的主要因素为使用时间、太阳辐射量(与时间是线性关系)、温度、湿度。对于隐身涂料仿真评价研究,目前还没有一个仿真评价模型来表述。因此,有必要建立隐身涂料仿真评估模型,提高隐身涂料的研究效率,缩短试验周期。
人工神经网络[7]是模拟生物脑结构和功能的一种信息处理系统,也可称为人工智能系统,其特有的自学习和联想记忆功能,使这种方法对解决影响因素复杂、难以用公式表达的问题特别有效。BP神经网络与其他理论建模相比较,建模关系数目没有限制,灵活性和预报精度较高,该网络在识别、预测和控制等方面得到很好的应用,可探索将其应用于隐身涂料的老化预测。但一般BP神经网络采用梯度下降算法,全局收敛能力差,收敛速率慢,易陷入局部极值点。遗传算法(GA)作为一种解决复杂问题的有效方法,是由美国密执安大学的John Holland教授于1975年首先提出来的,这种算法是以达尔文的生物进化论为启发而创建的,是基于生物进化中自然选择、适者生存和物种遗传思想的搜索算法。将GA同BP神经网络相结合,可以有效提高并行搜索能力,在全解空间寻优,易找到近似最优解[7-8]。
当然,隐身涂层寿命影响因素很多,如环境因素(高温、低温、湿热、盐雾、太阳暴晒等)、涂层树脂体系(丙烯酸、环氧、聚氨酯、氟树脂等)、隐身涂层对抗频谱(有光学、红外、雷达)等,对应其添加功能组分又相应有颜料、金属粉等。因此,隐身涂层老化性能的研究非常复杂,为了研究的方便性,本文选取具有代表性的高原环境条件,对光学伪装涂层的老化性能开展试验研究。通过制作氟碳类高耐候性光学伪装涂层试件,开展高原环境户外大气暴露试验,采集涂层的物理值如色差值、光泽、保光率随时间变化一些离散的样本数据,基于BP人工神经网络和GA进行数学建模,以涂层的初始物理量值和预测时间为输入,以预测时刻的物理量变化值为输出,对涂层物理量进行计算,建立隐身涂料预报模型,寻求涂层使用时间、太阳辐射量、环境温湿度与涂料保光率和色差变化之间的隐含关系,可以用来预测涂层物理量,从而得到涂层的有效寿命。
1 试验部分
1.1 试样制备
试样为经过防腐处理的钢板,尺寸为68 mm× 148 mm×0.5 mm,试样为氟碳改性聚氨酯光学隐身涂层样板,3块平行试样,编号为1号、2号、3号。
1.2 试验方法
环境试验参照GB/T9276—1996《涂层自然气候暴露试验方法》的规定执行,样本试验周期为2010年3月12日~2011年10月27日,试验地点为国家大气老化试验拉萨站。
2 基本BP神经网络
对于预测一般采用多层前向BP神经网络,该网络有一个源节点输入层、一个或多个隐含层、一个输出层。Robert Hecht-Nielsen于1989年证明了用一个3层网络即可模拟任意复杂的非线性问题。图1给出了多个输入一个输出的神经网络预测模型,为3层的网络模式,结构为:一个输入层,节点数为R;一个隐层,节点数为C;一个输出层,节点数为1;输入层到隐含层的权重为W=(Wij)R×C;(bj)1×C为隐含层各个神经元的阈值;(uj)1×C为隐层到输出层权重;b2为输出层阈值。

图1 神经网络结构图Fig.1 Structure of neural network
神经元的激励函数采用对数Sigmoid函数:

式中:a为控制函数斜率的参数,a>0;v为输入。
由于Sigmoid函数值域为(0,1),所以要先对样本数据进行映射处理,尽量使输入输出值均匀分布在0~1之间,考虑到激励函数不能取0或1,所以这里将数据处理时进一步缩小区间,设样本总体为S,某样本原始数据为sk,处理后数据为

这样保证处理后的数据在[0.1,0.9]之间,这样训练网络最后输出值都能达到这个值。BP算法先进行学习,即将历史数据输入网络中进行训练,具体步骤如下。
步骤1 设置网络参数、初始权值矩阵和阈值。设W(维数为R×C)为输入层到隐层的连接权值,B1(维数为1×C)为隐层阈值,W2(维数为C×1)为隐层到输出层权值,B2(维数为1×1)为隐层阈值。
步骤2 随机输入样本Sk=(sk1,sk2,…,skR),经过网络计算得出输出值:
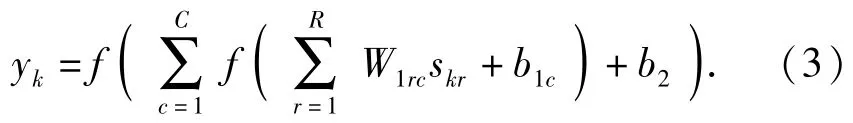
步骤3 将输出值与期望输出值dk比较,计算出误差:

步骤4 反向计算:当输出层的实际输出值与希望输出值不一样时就要对网络进行校正。校正是从后向前进行的。BP算法采用误差的负梯度来调整连接权,使其输出误差单调减少。可以采用每输入一个样本就调整一次,也可一次随机把所有样本都输入后,求出总的误差后进行调整,这里采用后一种方式进行调整。
重复步骤2、步骤3、步骤4,直到误差满足精度要求或达到规定迭代次数为止。
3 遗传算法全局优化网络
BP神经网络的学习关键是在步骤4,基本算法是基于梯度下降的,这种方法收敛速度慢,易振荡,而且易陷入局部极值点。GA是在整个解空间进行搜索,收敛速度快,而且易得到全局最优解。用GA对神经网络进行训练,能够很好地解决神经网络方法存在的问题。它的收敛性取决于染色体表示方式、初始群体、适应度函数、遗传算子的设计。
3.1 染色体表示
神经网络学习的目标是找到恰当的网络权值和阈值,使误差最小。GA一个个体的染色体表示对应于一个解,即对应于神经网络的权值和阈值,先将神经网络权值矩阵变形成一维矩阵,按W1、B1、W2、B2的次序将所有权值阈值连接在一起,形成GA实数编码的染色体表示。如图2所示,编码长度为R×C+C+C×1+1.

图2 染色体表示Fig.2 Chromosome representation
3.2 产生初始种群
按文献[8]中BP学习算法初权阈值取值方法,初始权值取为均匀分布在(-2.4/F,2.4/F)随机小数,其中F为所连单元的输入端个数。
3.3 适应度函数
用批处理的方式来训练网络,即把所有的样本组成一个训练周期,全部样本都一次输入网络后,计算出总的绝对误差能量:

作为个体的适应值,最小则越优。
3.4 两代竞争的选择算子
在遗传迭代过程中,若过早使群体趋于一致,则在后面迭代过程中是对少数甚至同一个体进行许多操作,而且很难跳出这个局部点,这样失去了遗传操作的内在并行性,就既浪费内存资源,又最终只得到这局部点附近的最优点,这就是“早熟”现象,为避免如此,就要在遗传过程中尽量保持群体的多样性,使个体中两两之间相似程度尽可能小,这里引入多维欧氏距离来计算个体二者之间的距离作为二者的相似程度,设个体x=(x1,x2,…,xn),y=(y1,y2,…,yn),则二者之间的欧氏距离为
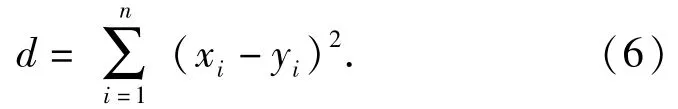
为避免“早熟”且不过多增加计算量,选取父代优秀个体参与到下一代的竞争,可选择3个中淘汰1个,或4个中淘汰2个的方式,本文用3个中淘汰1个的方式进行选择,从父代取出S(取S=C/2)个优秀个体与当代产生的C个个体中竞争,选出C个个体作为下一代。具体竞争方法是以3个为一组进行分组,每组两两之间求出欧氏距离后进行比较,找到距离最小的2个个体,说明这2个个体相似程度高,则淘汰其中适应度小的个体。这样就做到了尽量保持遗传过程中个体的多样性,避免了过早陷入局部极值点,保持了遗传算法内在并行性。同时,有更多的个体参与竞争(M+S),种群中的优秀个体(包括历代最优个体)一定能遗传到下一代,这样使搜索的局部能力得到加强,使收敛速度增快。
3.5 算术交叉算子
设选中的两父代个体为x1、x2,交叉后新生成个体为,则

式中:α为随机生成的数,满足0≤α≤1.
3.6 高斯变异算子
对于个体x=(x1,x2,…,xn),加入一个小的扰动,作为个体的变异,设个体变异后变为.随机生成变异基因位r,则
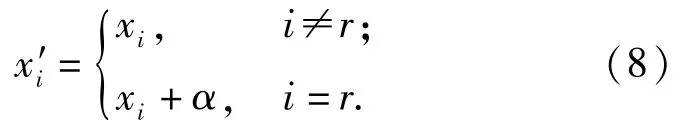
式中:α为(-2.4/F,2.4/F)随机小数。
3.7 爬山操作
当每代交叉、变异完成后,找出群体中的最优个体,通过领域搜索实施爬山操作,具体操作如下:
1)给最优个体一个小的扰动,做法同变异;
2)判断新的个体是否更优,更优则替换原个体。
重复1、2,直到达到一定操作次数为止。
3.8 遗传神经网络算法流程图
一般BP网络算法是基于梯度下降的,即利用误差反馈,权值阈值向误差对权值阈值梯度的反方向变化,使误差逐渐下降,遗传神经网络是利用GA来训练网络权值阈值,其流程图如图3所示。
4 在涂层老化性能评价中的应用
老化机理研究表明,老化降解主要是光引发的氧化和水解,其影响因素主要有阳光(特别是紫外线)、温度、氧气、水和污染物等。在野外自然界中,氧气含量和污染物含量基本恒定,可以认为影响涂层老化的因子是紫外线辐射量、温度、水(以湿度来表示)以及所经历的时间。涂层的有效性,主要根据色差ΔE和保光率来判断,色差ΔE随时间逐渐变大,保光率随时间逐渐变小,当色差ΔE大于3或保光率小于70%可认为涂层失效。在自然界中,涂层老化到失效时间较长,但目前试验时间短,只有12.5个月的时间,还没达到失效。为了能利用前12.5个月的数据来预测后几年的色差变化情况,达到预测涂层的失效时间的目的,本文建立预测模型来预测间隔某一段时间色差ΔE和保光率的变化值,从而计算出后面几年涂层色差和保光率变化情况。在模型中,以时间间隔、紫外线辐射总量、平均温度、平均湿度、初始时刻色差值ΔE和保光率为输入,以差值ΔE和保光率的变化值作为输出,建立神经网络预测模型。因此输入层神经元均为6,输出层为2,考虑本例实际情况,解决该问题的网络隐层神经元应该在4~12之间。

图3 改进遗传神经网络算法流程图Fig.3 Flow chart of improved genetic neural network algorithm
5 涂层老化预测实例
对涂层老化试验期间(2010年3月~2011年9月)的气象参数进行了统计,见表1,采集的参数包括:地面所受太阳紫外线辐射总量、月平均温度、月平均湿度和历年平均值,自然老化试验从3月12日开始,以天为单位,一定间隔后对涂层各值进行观测统计,得到试板观测值,以0时刻值为初始值,计算色差和保光率,取60°保光率进行计算。气象统计数据以月为单位,为了便于计算,将气象统计数据平均到天,最终,得到神经网络样本各值,即累计得出时间间隔,计算出该时间间隔内紫外线总量、平均温度、平均湿度、色差ΔE变化值、保光率变化值,如表2所示。
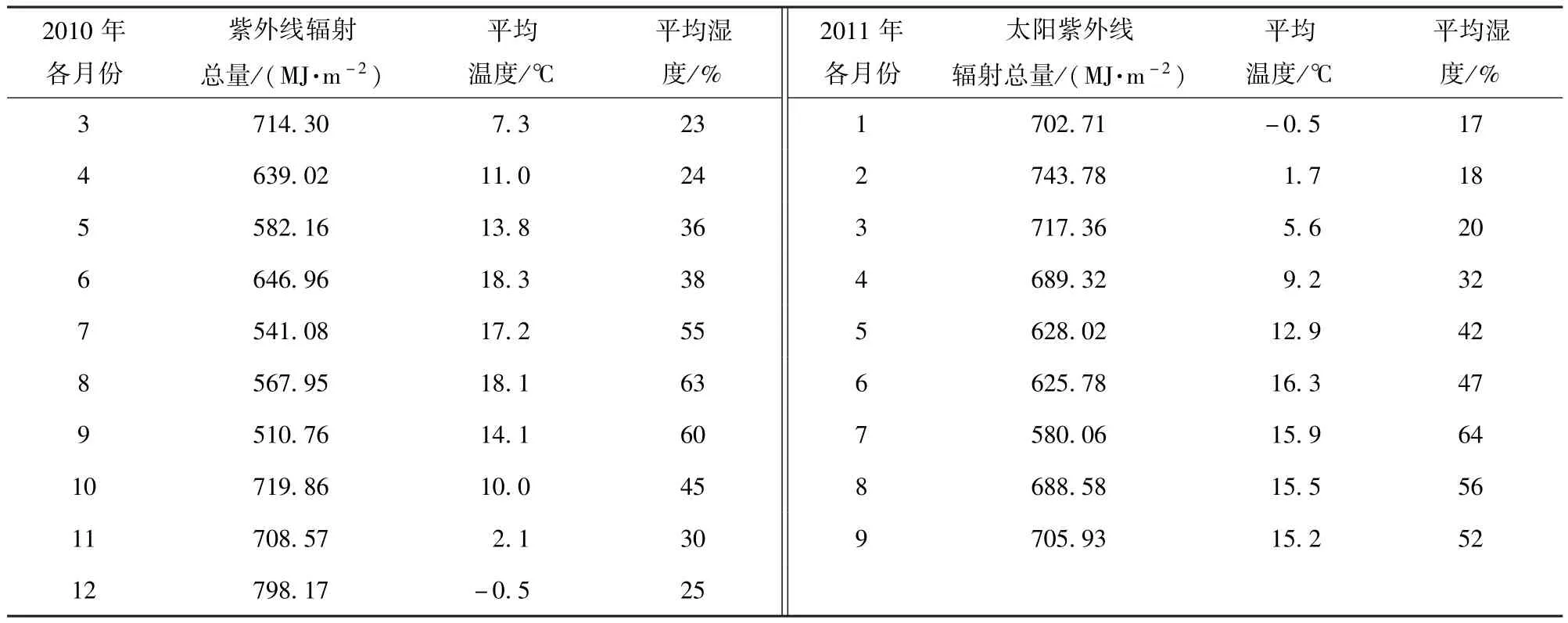
表1 试验周期内太阳紫外线辐射总量、月平均温度、月平均湿度及历年平均值Tab.1 Solar UV radiation,mean monthly temperature,mean monthly humidity and average value of pre vious years in test period

表2 神经网络样本表Tab.2 Samples of neural network
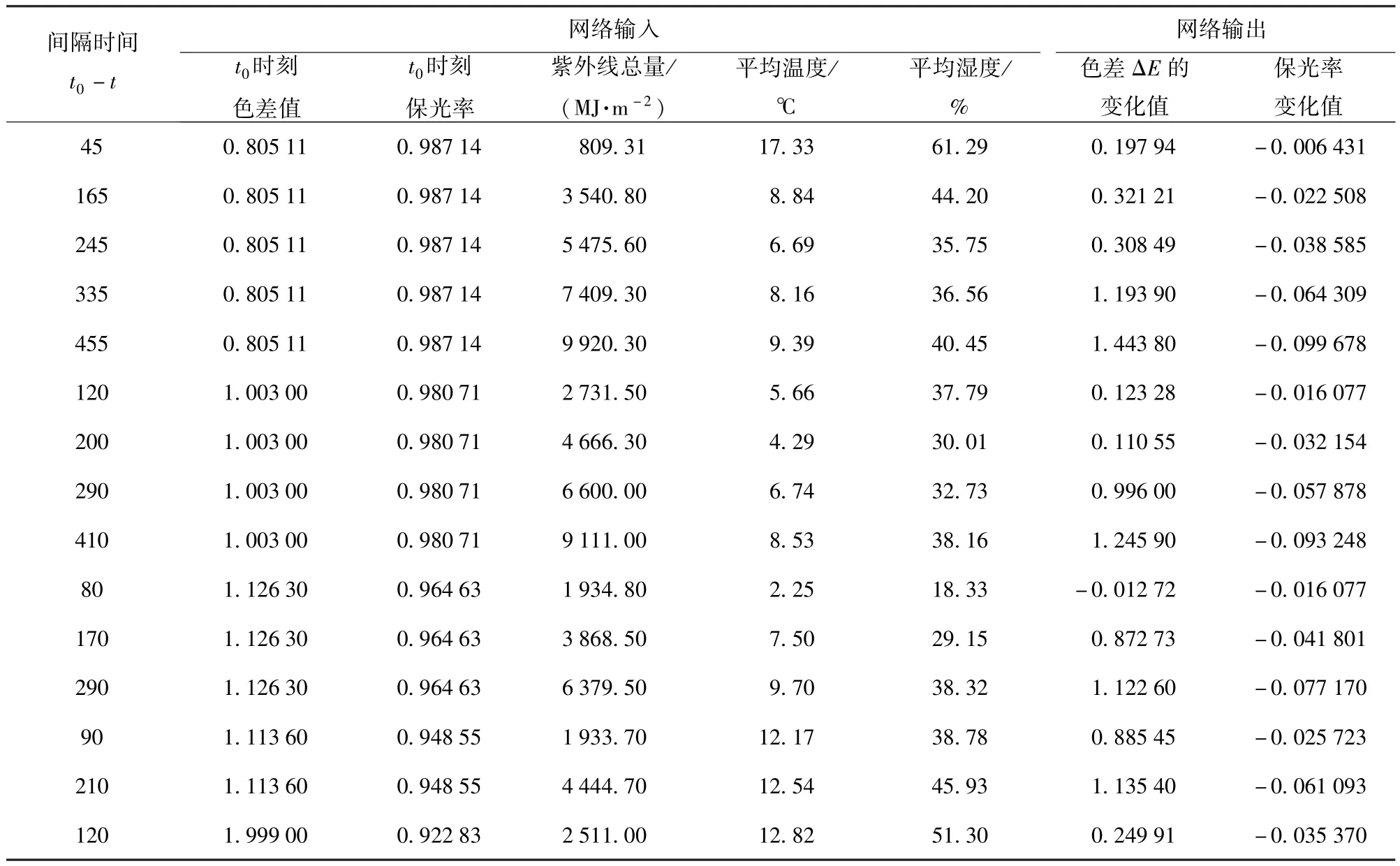
续表2
将样本数据输出到遗传神经网络进行训练,训练好的网络就可以用来预测。这里采用基于Visual studio 2008编程,来设计遗传神经网络训练程序和预报程序,遗传神经网络训练程序如图4所示,输入网络参数、样本数据后,可以进行网络训练,最终得到网络输出总误差,若达到期望值,则网络结构和权重数据就可以用来进行预测涂层物理量值变化值。

图4 遗传神经网络程序界面Fig.4 Programming interface of genetic neural network
预测程序界面为图5,该模型有两种预测功能:一是以2010年3月12日为初始试验时间,可以预测在此时间后任意时间涂层保光率和色差ΔE.输入涂层预测时间,点击“计算”,得到涂层的色差和保光率ΔE;二是计算涂层失效时间,和一段时间内保光率或色差ΔE随时间变化值。输入时间段起止时间和步长,点击“随时间变化”,得到保光率或色差ΔE随时间变化值,同时在程序界面右上角显示了保光率或色差失效时间。

图5 神经网络预测涂层物理量变化值和寿命Fig.5 Forecast of the change of coating physical quantity value and life using neural network
如表3所示,对比高原自然暴露试验380 d的试验数据,保光率为94.90%,而程序输出为95.19%,从模型输出结果和已进行的试验采集结果对比来看,由此可知此模型准确度高。

表3 试验数据与仿真输出数据对比Tab.3 Comparison of test data and simulation output data
6 结论
通过材料优化设计制备了高耐候性光学隐身涂层样板,并开展了高原自然环境暴露试验,利用采集的试验数据作为模型训练样本,建立了涂层老化过程中的各物理值变化值计算方法。从而确定了计算该类涂料耐老化性能BP预测模型。通过开展本文研究,得出以下两点结论:
1)基于BP神经网络和GA相结合,建立的遗传BP神经网络基本模型,可以用于隐身涂层老化性能的评价。依据此模型可预测该类涂层样板,在高原环境条件下的老化性能的变化情况,从试验结果和模型输出结果对比来看,模型准确度较高。
2)当训练样本数量较多时,计算精度较高,反之较低。通过试验验证,训练完后的神经网络模型,准确度高,可以满足工程的需要,只要给出判断寿命的临界指标,就可用于寿命计算。
(
)
[1]卢言利.有机涂层高原环境影响参数分析及老化机理研究[J].涂料工业,2012,42(4):12-18. LU Yan-li.Ageing mechanisms and influencing factors for organic coatings used in plateau environment[J].Paint&Coatings Industry,2012,42(4):12-18.(in Chinese)
[2]Buaer D R.Melamine/fomraldehyde closslinkers:characterization,network formation and crosslink degradation[J].Progress in Organic Coatings,1986,14(3):193-218.
[3]Armstrong R D,Jenkins A T A,Johnson B W.An investigation into the UV breakdown of thermoset polyester coatings using impedance spectroscopy[J].Corrosion Science,1995,37(10):1615-1625.
[4]Pappas S P.Weathering of coatings-formulation and evaluation[J].Progress in Organic Coatings,1989,17(2):107-114.
[5]Oosterbroek M,Larmmers R J,Van der Ven L G J,et al.Crack formation and stress development in an organic coating[J].Journal of Coatings Technology,1991,63(7):55-60.
[6]Ooterhold M,Glockner P.Influence of weathering on physical properties of clearcoats[J].Progress in Organic Coatings,2001,41(1):177-182.
[7]Sexton R S,Gupta J N D.Comparative evaluation of genetic algorithm and back propagation for training neural networks[J].Information Sciences,2000,129:45-59.
[8]吴红,吴值民.一种基于实数编码的遗传神经网络预测方法[J].计算机科学,2008,35(11):178-180. WU Hong,WU Zhi-min.A real number coding genetic neural network prediction model[J].Computer Science,2008,35(11):178-180.(in Chinese)
Evaluation Model of Aging Properties of Stealth Coatings Based on Genetic BP Neural Network
LU Yan-li,MU Jing-yang
(The First Engineers Scientific Research Institute,General Armaments Department,Wuxi 214035,Jiangsu,China)
In order to research the relationship between the physical values of coating aging in the natural environment and the environmental factors,a genetic BP neural network with real coding,arithmetic crossover,Gauss mutation and climbing operation is designed.The physical values of coating are calculated according to the environmental factors.Visual Studio 2008 is used for programming,and a program is developed for neural network training and prediction program.Finally,an example of field aging data of coating is used for network training and prediction.The results show that the proposed model can be used to calculate the ultimate life of the coating.The calculated values are similar to the measured values.The genetic neural network model can be used for prediction of coating life.
ordnance science and technology;stealth coating;aging-resistant performance;BP artificial neural network;genetic algorithm;life prediction
E951.4
A
1000-1093(2015)08-1580-07
10.3969/j.issn.1000-1093.2015.08.029
2014-11-21
国防科研项目(ZLA09081)
卢言利(1978—),男,工程师。E-mail:lyl-997@163.com

