基于关联维数迭代局部投影算法的装甲目标声信号去噪研究

丁凯，钱汉明，陈果，荣英佼，朱翼超，史俊超

（1.近地面探测技术重点实验室，江苏无锡214035；2.总装备部工程兵科研一所，江苏无锡214035）

基于关联维数迭代局部投影算法的装甲目标声信号去噪研究

丁凯1，2，钱汉明1，2，陈果1，2，荣英佼1，2，朱翼超1，2，史俊超2

（1.近地面探测技术重点实验室，江苏无锡214035；2.总装备部工程兵科研一所，江苏无锡214035）

为了抑制装甲目标声信号中包含的噪声成分，消除其对信号特征提取的不利影响，针对局部投影法中邻域半径选取困难的问题，提出了一种基于关联维数迭代的局部投影算法（CDBILPM）。对典型混沌系统Lorenz序列分别叠加不同噪声水平的高斯白噪声，得到信噪比为20 dB和10 dB的含噪信号，运用本算法对其进行去噪仿真实验。结果证明，本算法不仅简化了计算量，而且可以使Lorenz系统的动力结构得到良好的恢复。应用本算法对坦克和轮式装甲车两类装甲目标的实际声信号进行去噪处理，样本信号的噪声强度显著下降，关联维数减小，信号序列的吸引子结构由杂乱变得有序，说明了本算法可有效消除非线性信号中所含噪声。

兵器科学与技术；非线性；装甲目标；声信号；去噪；局部投影法

0 引言

智能地雷引信在接收装甲目标声信号时，由于外界环境的影响，难以避免地会混入噪声。目标声信号已经被证明了是一种复杂的非线性过程，其中包含混沌和分形机制［1］。而噪声会破坏非线性系统的混沌吸引子结构，掩盖其真实的动力学行为［2］，使其不变量（如Lyapunov指数、分形维数等）的计算失准，从而对目标的特征提取和识别产生不利影响。

由于非线性信号具有对初始条件敏感和宽频谱等特性，而噪声通常在频域上的带宽也较大，若采用传统的滤波去噪方法进行处理很难将噪声与信号分离，而且可能会破坏原信号所包含的确定性特征。针对非线性信号的噪声去除，发展起来了一些算法，其中，Hegger等［3］提出的局部投影方法（LPM）无需预知模型的先验信息，其主要思路是先对含噪信号进行相空间重构，然后将特征信号和噪声信号分别向高维相空间中的不同的子空间投影，再通过重构子空间分离特征信号和噪声信号，目前已成功应用到语音信号和机械振动信号去噪处理中。

LPM的关键是邻域半径的选取，确定邻域半径的方法大多依靠经验以及试探选取，Matassini等［4］提出了定量递归分析法，该方法虽然有效，但需要预先计算时间序列的定量递归图，在具体应用中显得比较复杂；Kern等［5］提出的邻域选取方法受噪声程度的影响比较严重，在应用上有所局限；阳建宏等［6］提出了一种自适应方式选取邻域大小的方法，韩敏等［7］结合奇异谱分析技术，提出了一种改进的邻域选择法，这两种方法提高了原算法的去噪能力，但受控参数较多，增加了计算的复杂性。

本文针对邻域半径的选取问题，提出了一种基于关联维数迭代局部投影算法（CDBI-LPM），对含噪混沌系统Lorenz序列进行了去噪仿真实验，通过对去噪前后的时域波形、吸引子相图以及关联维数进行了对比分析，验证了算法的有效性。而后，运用该算法对两类地面装甲目标（坦克、轮式装甲车）的实际声信号进行去噪，结果表明，经过处理，信号的噪声强度和关联维数均得到降低，系统吸引子相图由杂乱变得有序，信号噪声得到有效消除。

1 LPM基本原理

设一维含噪混沌时间序列由两部分组成:

式中:xn为无噪声混沌时间序列；ωn为噪声时间序列。根据Takens嵌入定理，将sn经过重构可以得到一个m维相空间［3］

式中:Sn表示m维相空间中的第n个相点；m表示嵌入维数；子表示延迟时间。

存在sn的近似估计值，可用映射关系表示为

（3）式在Sn点邻域可线性展开为

设零子空间的维数为Q，则只要找到Q个正交的矢量aq（q=1，2，…，Q），使得在这Q个矢量上有最小的局部投影值。Zn在零子空间的投影为，这里的aq为归一化矢量。因局部投影局限在相点Sn的邻域un内，选择合适的aq，使得达到最小值。因aq· aq′=0（q≠q′，q′=1，2，…，Q），引入Lagrange乘子λq，并且‖aq‖=1，则最小化Lagrange算子为

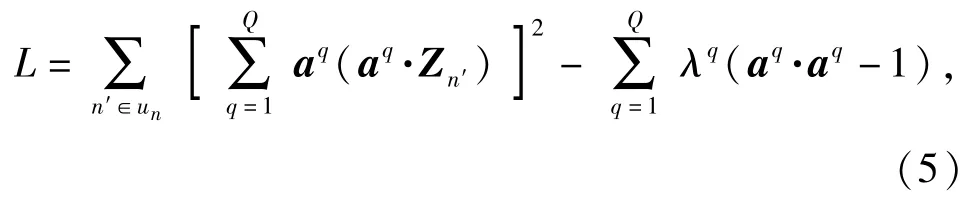
对于每个独立的q，有

式中:C为Zn′在邻域un内的一个m×m阶协方差矩阵，

由（6）式可得C的特征值和正交特征向量。理论上，由噪声引起的分量就是Q个最小特征值所对应的特征矢量，这样，减去矢量Zn中的噪声成分

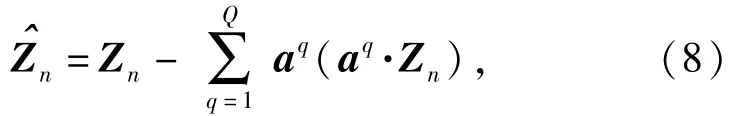
得到局部投影去噪算法的最终算式为

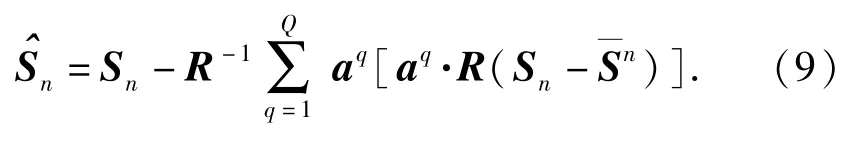
2 CDBI-LPM及仿真实验

2.1 CDBI-LPM原理

LPM去噪总体而言可分为3个步骤:1）重构信号时间序列的相空间；2）估计动力学系统模型；3）调整含噪点的轨迹，使之适合估计的模型又不能偏离原先的轨迹太远。

在进行以上这3个步骤的过程中，需要对相空间重构参数和去噪模型的调整参数进行选取。

相空间重构参数主要包括嵌入维数m和延迟时间子，这里采用C-C法［8］进行计算。算法的关键是对邻域半径（即调整参数）ε的选取。ε的大小由时间序列包含的噪声大小决定。通常若ε取得过小，会造成邻域内的邻近点数呈稀疏状，引起去噪后信号的波形剧烈震荡；而ε过大，会使得分段线性逼近的效果不明显，不能很好反映某些细微部分的结构［9］。因此，邻域半径的选取直接影响到局部投影法去噪效果的优劣。

Schreiber［10］提出了根据时间序列的噪声强度来估计最小邻域半径，对于噪声强度的计算，文献［11］采用了关联积分估算法，文献［12］和文献［13］采用了计算时间序列的标准偏差来近似估计。后者的方法对于（1）式所示的含噪时间序列，将噪声强度表示为

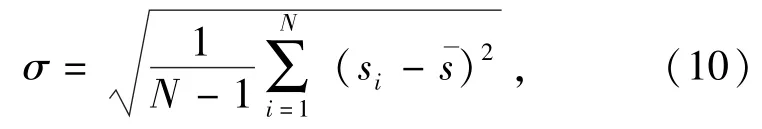
由于混沌系统产生于低维动力学系统，而噪声是由高维动力学系统产生的，包含噪声的混沌系统的维数将迅速增加，造成维数估计不准确［14］。利用这条性质，可以将分数维数理论中的关联维数引入，以此作为量化判断去噪效果的依据，关联维数可参照（11）式来计算:

式中:m为嵌入维；r为尺度；C（m，N，r，t）代表嵌入时间序列的关联积分。

在此，本文提出了一种基于关联维数迭代优化（CDBI）的方法，把对邻域半径的一次性选择转变为多次选择，以期达到更好的去噪效果。算法的计算步骤如下:

步骤1 估计出含噪信号s0的噪声强度ε0，作为初始邻域半径，并确定重构参数m和子，代入局部投影去噪算法，得到去噪后的信号s1，计算出s1的关联维数D1；

步骤2 估算s1的噪声强度ε1，代入局部投影去噪算法，得到去噪后的信号s2，计算出s2的关联维数D2；

步骤3 继续依照步骤2，对s2，s3，…，sn进行局部投影法去噪，得到关联维数D3，D4，…，Dn+1；

步骤4 根据D1，D2，…，Dn+1绘制关联维数曲线，最优去噪结果应选择曲线开始变缓和的点，设该为第p点，一般可由|Dp+1-Dp|取得全局最小值来判定。则sp就是最终去噪后的序列，Dp为该序列的关联维数。

CDBI-LPM的流程图如图1所示。

图1 CDBI-LPM流程图Fig.1 Flow chart of CDBI-LPM

2.2 去噪仿真实验

去噪仿真实验以Lorenz方程产生的混沌时间序列为研究对象，其表达式为

选取模型参数σ=10，γ=28，b=8/3，积分步长设为0.005，采用龙格-库塔积分法采样得到2 000点x分量的序列，如图2所示。

在无噪声情况下，Lorenz系统吸引子在xy平面上的投影相图如图3所示，可见存在明显的吸引子。在无噪Lorenz时间序列上分别叠加不同噪声水平的高斯白噪声，得到信噪比20 dB和10 dB的含噪信号。这里将信噪比为20 dB和10 dB的两种信号分别以L1和L2表示。其时域波形分别如图4（a）和图4（b）所示，为了看清细节，取了前500采样点数据应用C-C法计算得到L1和L2的相空间重构参数均为m=5，子=8.重构得到L1和L2的吸引子相图分别如图5（a）和图5（b）所示。

图2 Lorenz序列x分量时域波形Fig.2 Time domain waveform of x component of Lorenz sequence

图3 无噪声Lorenz序列的吸引子相图Fig.3 Attractor track of Lorenz sequence without noise

图4 加噪Lorenz序列的时域波形Fig.4 Time domain waveforms of Lorenz sequence for adding noise

图5 加噪Lorenz序列的吸引子相图Fig.5 Attractor tracks of Lorenz sequences with noise

由图5可以看出，加噪后的Lorenz序列的吸引子相图开始变得很不规则，其结构被噪声破坏，噪声越大对其影响越严重。根据叠加噪声的强度，作为初始邻域半径，应用CBDI-LPM对L1和L2进行去噪，得到关联维数曲线如图6所示。

由图6可以看出，L1和L2分别经过了4次和5次迭代，曲线开始变缓和且斜率保持近似为0.分别选择相应的去噪后信号作为最优结果。在对多个序列进行仿真计算的过程中发现，通过3～5次迭代，一般就可以获得比较理想的去噪效果，过多的迭代计算会导致信号产生失真和变形，反而对去噪不利。L1和L2经过去噪后的吸引子相图和时域波形分别如图7和图8所示。

由图7可见，经过CDBI-LPM的去噪处理，加噪Lorenz信号的吸引子相图得到了很好的恢复，曲线比较平滑，结构清晰可见。由图8可知，L1和L2中包含的噪声都得到了有效的抑制，时域波形变得较为平滑。无噪声Lorenz信号的关联维数为1.560 3，经过计算得到了L1和L2去噪前后的关联维数，列于表1.

图6 去噪关联维数曲线Fig.6 Correlation dimension curves of noise reduction

图7 去噪后Lorenz序列的吸引子相图Fig.7 Attractor tracks of Lorenz sequences after noise reduction

表1 L1和L2去噪前后关联维数Tab.1 Correlation dimensions of L1&L2 before and after noise reduction

从表1可以看出，L1和L2去噪后序列的关联维数均与无噪序列的关联维数十分接近。对Lorenz序列的仿真计算结果说明，噪声得到了有效抑制，Lorenz系统动力结构得到较好的恢复。

图8 去噪后Lorenz序列的时域波形Fig.8 Time domain waveforms of Lorenz sequences after noise reduction

仿真算例证明了本算法的有效性，而且，相较于文献［4］和文献［6］所述的方法，本算法受控参数少，只有噪声强度一个受控参数，简化了计算量；并且，一般通过5次以下迭代就可取得良好的效果，可获得最优的邻域半径，计算速度较快。

3 实际信号去噪

本文选取了坦克和轮式装甲车两类目标的实测声信号为研究对象，分别表示为目标A和目标B.利用CDBI-LPM，对样本信号进行非线性去噪。目标信号去噪前的时域波形如图9所示。

计算各样本时间序列的相空间重构参数，分别得到嵌入维数和时间延迟；再对其进行噪声强度估计，作为初始邻域半径。参数均列于表2.

表2 样本信号局部投影去噪参数Tab.2 Noise reduction parameters of sample signals

根据表2中参数，利用CDBI-LPM对样本信号进行去噪，得到去噪前后信号的相空间吸引子轨迹图，如图10所示。

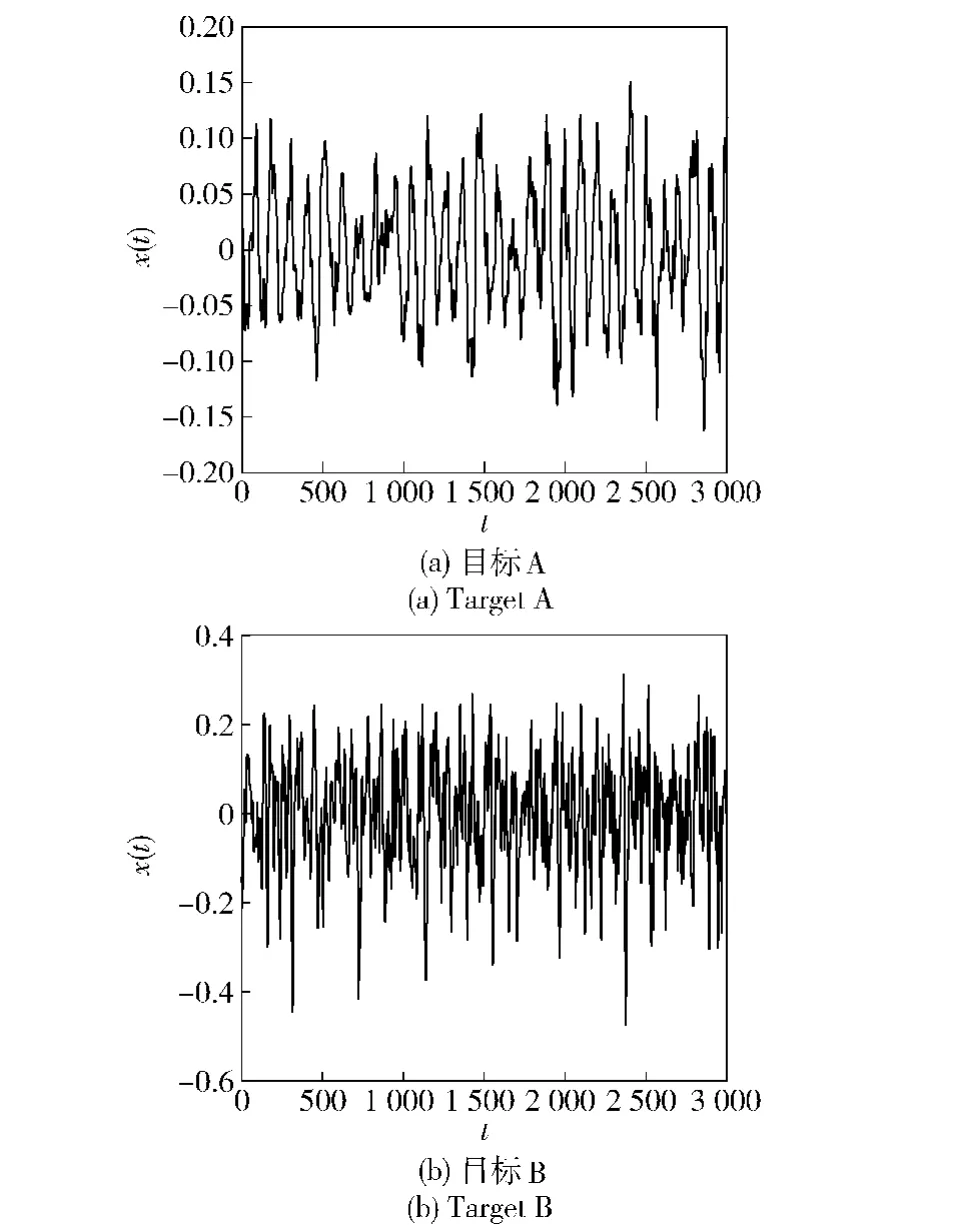
图9 目标样本信号的时域波形Fig.9 Time domain waveforms of sample signals

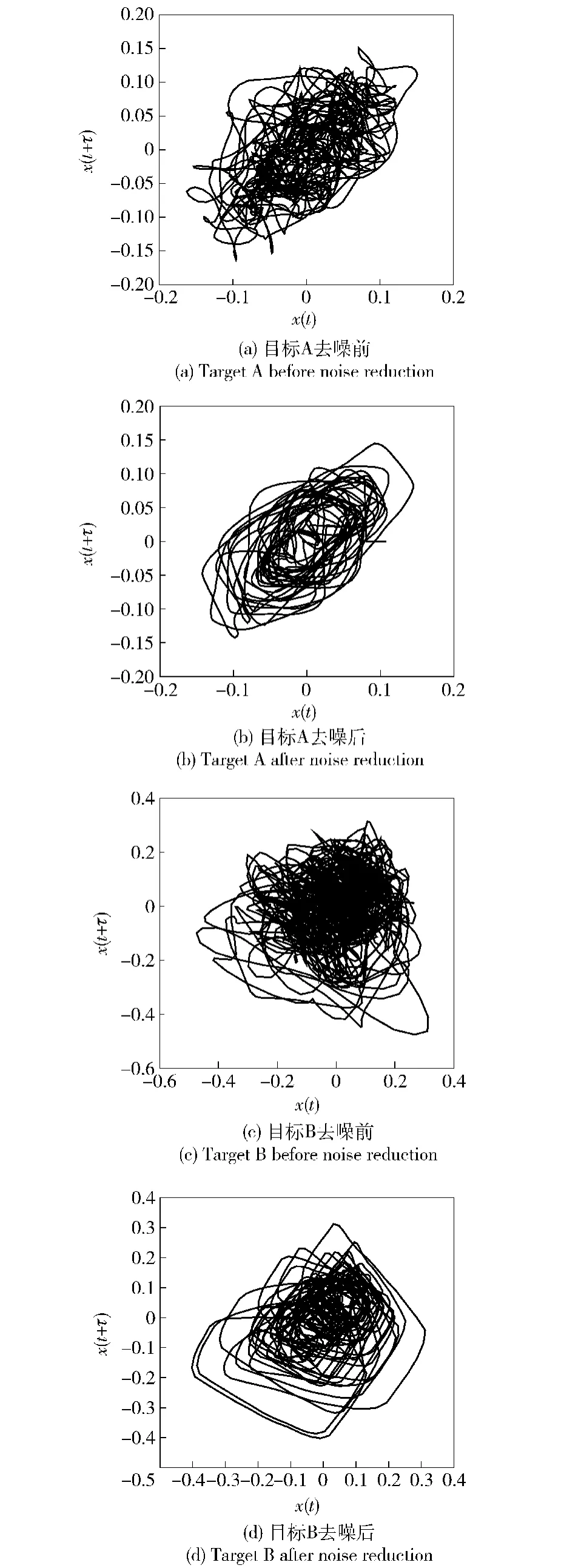
图10 去噪前后样本序列吸引子相图Fig.10 Attractor tracks of sample sequences before and after noise reduction

从图10可以看出，经过去噪，目标样本信号的相空间吸引子轨迹变化明显，从杂乱无章变得有序，包含的混沌特性得到较好体现。图11显示了样本信号经过去噪后的时域波形。

由图11和图9对比可以看出，经过去噪，样本信号的时域波形比去噪前更加平滑，噪声得到了有效的抑制。为了量化分析去噪效果，对样本信号去噪前后的噪声强度和关联维数进行估计，计算结果如表3所示。

表3 去噪前后参数对比Tab.3 Parameters before and after noise reduction

由表3中的数据可以看出，经过CDBI-LPM的去噪处理后，样本信号的噪声强度得到降低，关联维数明显减小，说明了原目标声信号所包含的噪声得到了有效消除。

图11 去噪后样本信号时域波形Fig.11 Time domain waveforms after noise reduction

4 结论

非线性信号的去噪处理是对其后续进行特征提取和模式识别的前提和关键步骤。本文在局部投影算法的基础上提出了一种优化邻域半径选取的改进算法，与其他算法相比，受控参数较少，计算简便；同时迭代优化可提高参数的估计精度。经过对含噪Lorenz序列的去噪仿真，以及对两类装甲目标实际声信号的去噪处理，结果表明本文方法可以有效去除目标声信号所包含的噪声，信号的非线性特征可以得到更好的体现，从而能够为目标声信号特征的准确提取创造有利条件。

本算法可应用于智能地雷引信对目标声信号的预处理中，提高引信的信噪比，增强其探测目标的可靠性。

（

）

［1］ 丁庆海，庄志洪，祝龙石，等.混沌、分形和小波理论在被动声信号特征提取中的应用［J］.声学学报，1999，24（2）:197-203. DING Qing-hai，ZHUANG Zhi-hong，ZHU Long-shi，et al.Application of the chaos，fractal and wavelet theories to the feature extraction of passive acoustic signal［J］.Acta Acoustica，1999，24（2）: 197-203.（in Chinese）

［2］ Kostelich E J，Schreiber T.Noise reduction in chaotic time series:a survey of common methods［J］.Physical Review E，1993，48（3）: 1752-1763.

［3］ Hegger R，Kantz H，Matassini L.Noise reduction for human speech signals by local projections in embedding spaces［J］.IEEE Transactions on Circuits and Systems-I:Fundamental Theory and Applications，200l，48（12）:1454-1461.

［4］ Matassini L，Kantz H.Optimizing of recurrence plots for noise reduction［J］.Physical Review E，2002，65（2）:1-6.

［5］ Kern A，Steeb W H，Stoop R.Projective noise cleaning with dynamic neighborhood selection［J］.International Journal of Modem Physics C，2000，11（1）:125-146.

［6］ 阳建宏，徐金梧，杨德斌，等.邻域自适应选取的局部投影非线性降噪方法［J］.振动与冲击，2006，25（4）:64-67，176. YANG Jian-hong，XU Jin-wu，YANG De-bin，et al.Nonlinear noise reduction method by local projection with adaptive neighborhood section［J］.Journal of Vibration and Shock，2006，25（4）:64-67，176.（in Chinese）

［7］ 韩敏，项牧.局部投影去噪的一种改进的邻域选取方法［J］.系统工程学报，2009，24（4）:392-398. HAN Min，XIANG Mu.An improved neighborhood selection method for local projection noise reduction［J］.Journal of System Engineering，2009，24（4）:392-398.（in Chinese）

［8］ Kim H S，Eykholt R，Salas J D.Nonlinear dynamics，delay times and embedding windows［J］.Physica D，1999，127:48-60.

［9］ 何卫锋，程礼，李小刚，等.非线性消噪的LP方法在振动信号分析中的应用［J］.振动工程学报，2004，17（4）:408-411. HE Wei-feng，CHENG Li，LI Xiao-gang，et al.Nonlinear noise reduction and its application to the vibration signal analysis［J］. Journal of Vibration Engineering，2004，17（4）:408-411.（in Chinese）

［10］ Schreiber T.Determination of the noise level of chaotic time series［J］.Physical Review E，1993，48（1）:13-16.

［11］ 王洪超，李亚安.局部投影降噪算法邻域半径参数的选择研究［J］.系统仿真学报，2007，19（4）:805-807，819. WANG Hong-chao，LI Ya-an.Determination of neighborhood size parameter of local projective algorithm for noise reduction［J］. Journal of System Simulation，2007，19（4）:805-807，819.（in Chinese）

［12］ 邢士勇，金海薇，郑海起，等.基于改进局部投影算法的非线性时间序列降噪［J］.军械工程学院学报，2007，19（2）:41-43. XING Shi-yong，JIN Hai-wei，ZHENG Hai-qi，et al.Noise reduction of nonlinear time series based on the improved local projective method［J］.Journal of Ordnance Engineering College，2007，19（2）:41-43.（in Chinese）

［13］ 郑宏民，李亚安，陈澜.基于局部投影算法的舰船信号降噪处理研究［J］.西北工业大学学报，2011，29（4）:569-574. ZHENG Hong-min，LI Ya-an，CHEN Lan.Noise reduction of ship signals based on the local projective algorithm［J］.Journal of Northwestern Polytechnical University，2011，29（4）:569-574.（in Chinese）

［14］ Krakovsk A.Noise reduction based on dynamics reconstruction［J］.Measurement Science Review，2001，1（1）:21-24.

Noise Reduction of Acoustic Signals from Armored Vehicles Based on CDBI-LPM

DING Kai1，2，QIAN Han-ming1，2，CHEN Guo1，2，RONG Ying-jiao1，2，ZHU Yi-chao1，2，SHI Jun-chao2
（1.Science and Technology on Near-Surface Detection Laboratory，Wuxi 214035，Jiangsu，China；2.The First Engineers Scientific Research Institute，the General Armaments Department，Wuxi 214035，Jiangsu，China）

A correlation dimension-based iteration-local projective method（CDBI-LPM）is proposed to reduce the noise in the acoustic signals from the armored vehicles and eliminate the harmful effects on feature extraction.20 dB and 10 dB（SNR）noisy signals are obtained by adding the different Gaussian white noises to the Lorenz sequence of a typical chaos system.The noise reduction simulation results show that the proposed method not only reduces the amount of computation，but also efficiently recovers the dynamic structure of Lorenz system.The application of the method in the noise reduction of actual acoustic signals from tanks and wheeled armored vehicles shows that the noise intensities of sample signals are significantly reduced，the correlation dimensions decrease，and the disorder attractor structures of the signal series get order as well.This indicates that the proposed method could efficiently reduce the noise in the nonlinear signals.

ordnance science and technology；nonlinearity；armored vehicle；acoustic signal；noise reduction；local projection method

TJ4；TN911.7

A

1000-1093（2015）07-1181-07

10.3969/j.issn.1000-1093.2015.07.005

2014-11-15

总装备部预先研究项目（40407010302）

丁凯（1983—），男，工程师。E-mail:winfast113@sina.com