弹箭非线性角运动稳定性Hopf分岔分析

钟扬威，王良明，傅健，常思江

（南京理工大学能源与动力工程学院，江苏南京210094）

弹箭非线性角运动稳定性Hopf分岔分析

钟扬威，王良明，傅健，常思江

（南京理工大学能源与动力工程学院，江苏南京210094）

为了分析弹箭的角运动稳定性，推导了弹箭的非线性角运动方程组，给出弹箭的非线性角运动Hopf分岔分析方法。以某型火箭弹高原试验为例，选取空气密度作为分岔参数，采用霍尔维茨判据判断了系统的稳定性，并确定了分岔点。由中心流形定理对系统进行降维，计算了Hopf分岔的3阶规范形，并作出了系统的分岔图，分析了分岔参数对极限环摆幅的影响。进行了仿真验证，结果表明，采用分岔分析方法能准确判断系统的稳定性及分析系统的极限环运动。

兵器科学与技术；非线性角运动；运动稳定性；Hopf分岔

0 引言

在火箭弹的高原遥测试验过程中，观测到大射角射击时多次出现大攻角锥形运动，使得射程减小，这种现象可能是非线性运动造成的。对于弹箭的非线性角运动分析，文献［1］中推导了复攻角模型，并借助平均法等定性方法理论分析了不同情况下的非线性角运动规律。文献［2］在文献［1］模型的基础上研究了非旋转大长径比弹箭在非线性气动力作用下产生极限平面摆动的机理及其抑制措施。文献［3］推导一个较为复杂的保留了几何非线性和气动非线性的复攻角模型，但未涉及到具体分析。文献［4］通过对大长径比无控低旋火箭弹的卷弧尾翼在3种不同安装位置时的气动特性进行数值计算，得出火箭弹在飞行过程中确实会出现锥形运动且尾翼安装方式对锥形运动会产生影响，证明了反装反向滚转卷弧形尾翼可以抑制低旋无控火箭弹的锥形运动。文献［5］考察了章动运动条件下的自旋弹体运动模型，并分析了线性化模型的稳定性，计算了自旋弹体的稳定性临界转速与临界锥角。文献［6］建立了章动和进动的复合运动模型，根据线性化模型分析了弹体章动及进动运动的相互关系，给出了自旋弹体章动运动稳定性条件。文献［7］综合考虑弹体姿态运动和位移运动建立了旋转弹锥形运动的动力学模型，采用李雅普诺夫一级近似方法，给出了弹道顶点附近弹体锥形运动的稳定判据。文献［8］给出了火箭锥形运动的微分方程组，文献［9-10］在该方程组的基础上通过小偏差线性化方法研究了火箭弹在小锥角情况下圆锥运动渐进稳定条件及收敛速度计算方法，并提出了提高火箭弹圆锥运动稳定性的方法。文献［11-12］基于陀螺线性扰动运动方程研究了旋转导弹的锥形运动稳定性问题。事实上，锥形运动对应于常微分方程中的极限环问题，因此，可采用常微分方程稳定性分岔理论进行研究。

本文建立了新的弹箭非线性角运动方程组，该方程组尽可能完整地保留了几何非线性及气动力非线性。给出了基于中心流形定理和规范形理论的弹箭非线性角运动稳定性Hopf分岔分析方法。结合某型火箭弹在高原射击时的参数，分析了以密度作为分岔参数时火箭弹非线性角运动的分岔特性。最后在给定初始条件下进行了数值模拟，验证了分岔分析方法结果正确性。

1 弹箭非线性角运动方程

1.1 坐标系的定义［1］

1）地面坐标系OExyz:其原点OE在炮口断面中心，OEx轴沿着水平线指向目标，OEy轴垂直于OEx轴，铅直向上为正，OEz轴按右手法则确定。地面坐标系为动坐标系，在忽略地球自转的情况下可将其视为惯性系。

2）基准坐标系Oxryrzr:由地面坐标系平移至弹箭质心O而成，随质心一起平动。

3）弹道坐标系Oxtytzt:其Oxt轴沿质心速度矢量v的方向，Oyt轴在包含速度矢量v的铅垂面内垂直于Oxt轴，向上为正，Ozt轴按右手法则确定。

4）第2弹轴坐标系Oξηζ:其Oξ轴为弹轴，指向弹头方向为正。该系由弹道坐标系经过绕Ozt轴和Oη轴的分别旋转δ1和δ2而来，则Oη轴在包含速度矢量v的铅垂面内垂直于Oξ轴，向上为正。

该系还可由基准系经三次旋转而来，第一次是基准坐标系绕Ozn轴正向右旋φ1角到达Oξ′η′zn，第二次是Oξ′η′zn系绕Oη′轴负向右旋φ2角到达Oξη′ζ′，第三次是Oξη′ζ′系绕Oξ左旋β角得来。

第2弹轴坐标系的转动角速度ω1为

5）弹体坐标系OXbYbZb:其OXb轴与弹轴平行；OYb轴垂直OXb轴，并在弹箭纵向平面内，向上为正；OZb轴满足右手法则。

此坐标系可由第2弹轴坐标系绕弹轴转过-β+γ角而得到，其转动角速度矢量为

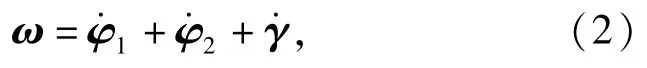
1.2 坐标转换矩阵

1）弹道坐标系与第2弹轴坐标系间的转换矩阵L（δ1，δ2）为

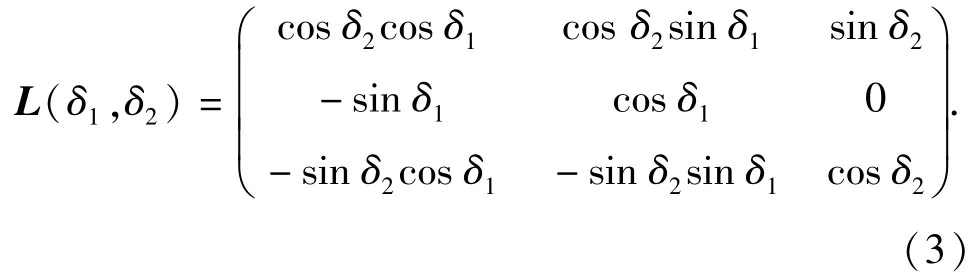
2）基准坐标系与弹道坐标系间的转换矩阵L（θ1，ψ2）为

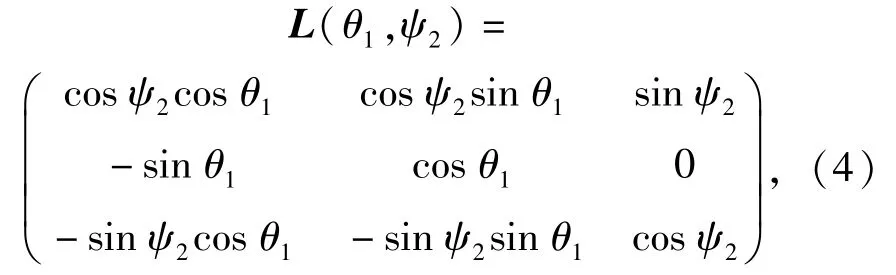
式中:θ1、ψ2分别为速度高低角和方位角。

1.3 弹箭非线性角运动方程推导

1.3.1 弹箭质心运动的动力学方程

弹箭质心运动方程组的矢量形式描述［1］如下:

式中:m为弹丸质量；F为弹丸受到的气动力的合力；ωt为弹道坐标系的转动角速度。将方程向第2弹轴坐标系投影得

式中:Fx、Fy、Fz为气动力F在弹道坐标系3轴上的分量。（6）式等号左边两项计算如下:

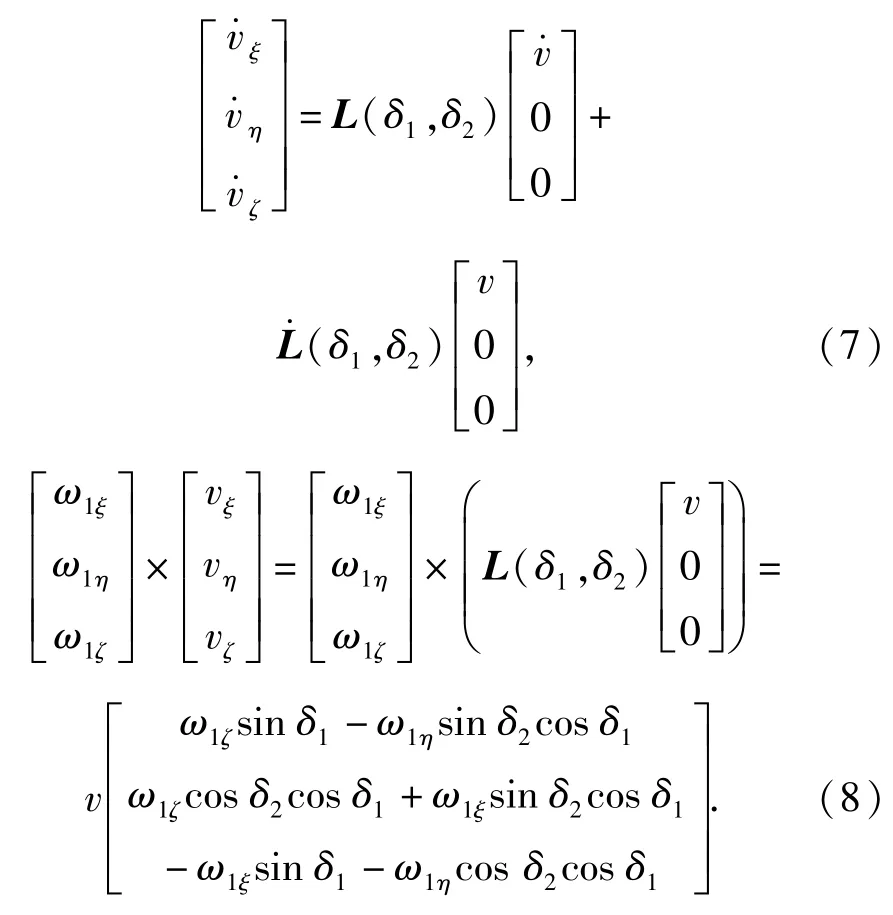
将（7）式、（8）式代入（6）式，并在等号两边同时乘上LT（δ1，δ2），则有

式中:G为弹箭重力。

整理（9）式得

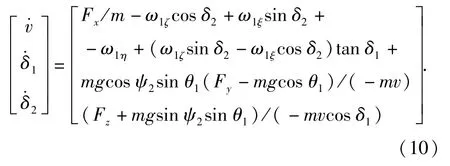
1.3.2 弹箭绕心运动的动力学方程

弹箭绕质心的转动方程用矢量形式描述［1］如下:

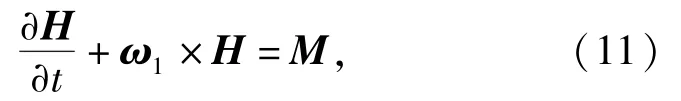
式中:H为弹箭对质心的动量矩；M为弹箭所受外力对质心的合力矩。

方程左边的两项计算如下:

式中:A、C分别为弹箭的赤道转动惯量和极转动惯量；弹体坐标系的转动角速度ω和第2弹轴坐标系的转动角速度ω1的表达式分别为

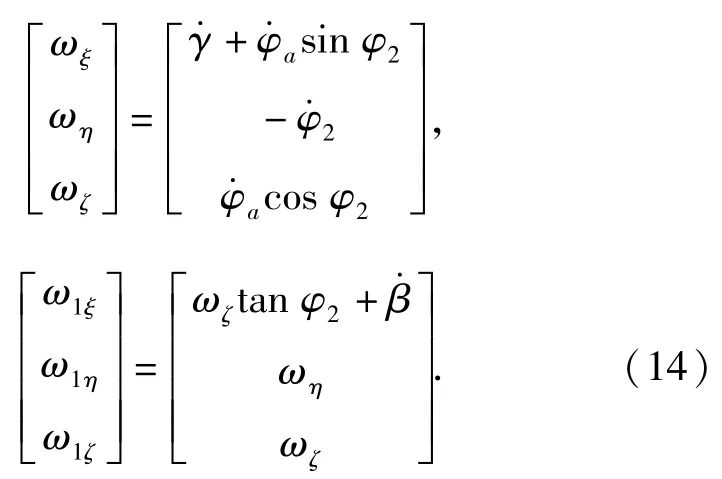
整理（11）式～（14）式可以得到以第2弹轴坐标系为参考系的绕心运动的动力学方程组为

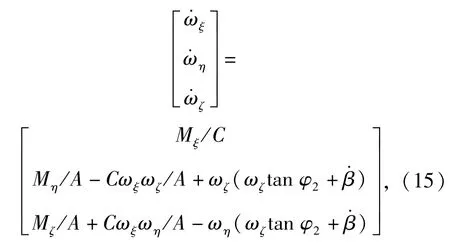
式中:Mξ、Mη、Mζ为力矩M在第2弹轴坐标系3轴上的分量。

1.3.3 弹箭非线性角运动方程

对于弹箭的角运动，主要关心的是δ1、δ2、ωη、ωζ的变化情况，故选取这4个量作为状态变量x=［δ1δ2ωηωζ］T.

弹箭飞行过程中，有sin β≈sin ψ2sin δ1/cos δ2，δ2≈φ2-ψ2，则

角度单位为弧度时，ψ2和的量级为10-4和 10-5，在攻角和摆动角速度较大时，经估算分析，相对于ωζtan φ2为小量，故取、φ2≈δ2.则ω和 ω1关系为

将第2弹轴坐标系的转动角速度代入到δ1、δ2、ωη、ωζ的方程中，不计重力，得到弹箭的非线性角运动方程组如下:

根据文献［1，13］，考虑气动力和力矩的最简非线性形式时，升力系数导数、静力矩系数、赤道阻尼力矩系数、马格努斯力矩系数可统一表示为以下多项式形式:

式中:δ为弹箭的总攻角，cos δ=cos δ2cos δ1；ct为上述的气动系数；c0、c2分别为气动系数的线性项和立方项。

方程组中包含了三角函数及其乘积，推导过程未涉及到三角函数的线性化问题，这体现了该方程组保留了几何非线性。因此，该方程组具有普遍性，适用于弹箭的非线性角运动稳定性分析。

2 弹箭非线性角运动分岔分析方法

2.1 非线性角运动方程分岔点计算

将弹箭所受的气动力和力矩代入到角运动方程中得

式中:S、l、d分别为弹箭的参考面积、长度和直径。

令方程组（20）式等号右边为0，求得O［0000］T为系统的平衡点。（20）式在平衡点处的雅克比矩阵为

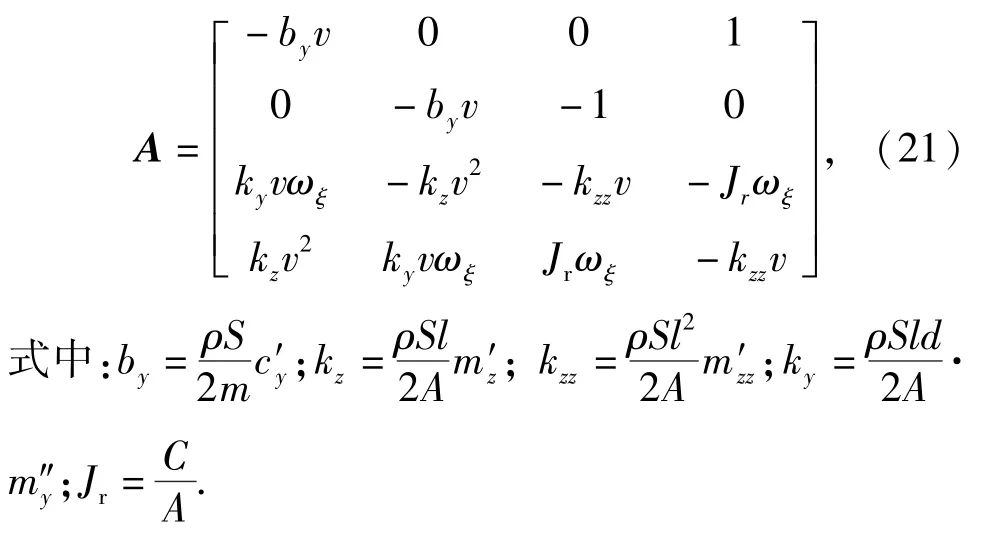
求出A的特征多项式，选取分岔参数μ，当参数μ变化时，根据霍尔维茨判据判断系统稳定性的变化，稳定性发生改变的点即为分岔点μ0.此时特征多项式有一对纯虚的特征根和一对实部为负的特征根（实部为正时，系统不稳定，这是实际中不关心的），求出系统在分岔点处的特征值λ1、λ2、λ3、λ4及特征向量ξ1、ξ2、ξ3、ξ4.

2.2 非线性角运动方程降维

四维角运动方程直接进行分岔分析比较困难，需要对其进行降维。在分岔点处，系统特征多项式有一对纯虚的特征根和一对实部为负的特征根，此时存在二维中心流形，可采用中心流形定理对系统进行降维［14］。

引入非奇异线性变换x=py，其中y=［y1y2y3y4］T，其中p为A的第2和第4个特征值所对应的特征向量的实部和虚部所构成的方阵。令u=［y1y2］T，v=［y3y4］T，代入系统方程得

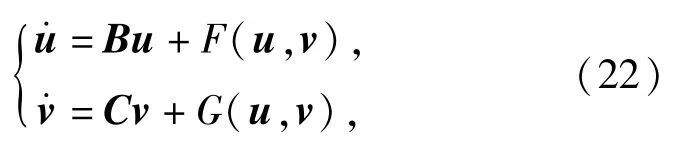
式中:B、C分别为两个方程的雅克比矩阵；F（u，v）和G（u，v）为方程组的非线性项。

由中心流形定理，可以把v表示为v=h（u），其中h（0）=h′（0）=0.为确定h（u），将v=h（u）代入（22）式的第2式，利用求导的链式法则，有

再利用第1式整理得到h（u）的微分方程

精确求解h（u）有困难，可以根据所需要中心流形的阶数假设方程

将（25）式代入到h（u）的微分方程，根据各项系数对应相等解出aijk、bijk，即得到v=h（u）的表达式.将h（u）代入（22）式中的第1式，即可得到中心流形上流的约化方程

2.3 非线性角运动方程极限环计算

将约化后的方程写成如下形式:

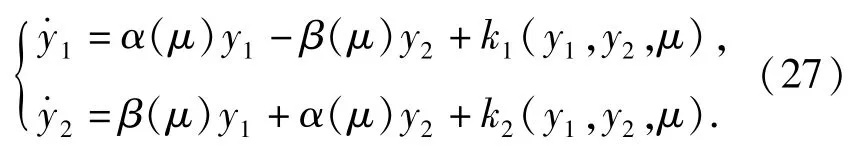
根据规范形理论［15］，其3阶规范形为

引入极坐标变换y1=rcos θ，y2=rsin θ，得到如下方程:

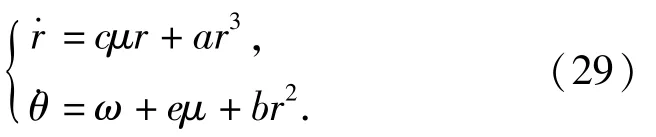
由此得到系统的近似平衡方程cμr+ar3=0.系统的极限环由cμr+ar3=0的非零解决定。极限环的摆幅，周期T=2π/ω.

当a≠0，c≠0时，系统在μ=0处出现Hopf分岔，其分岔特性为

1）当c＞0和a＞0时，平衡点对μ＞0不稳定，对μ＜0渐进稳定，当μ＜0存在不稳定极限环；

2）当c＞0和a＜0时，平衡点对μ＞0不稳定，对μ＜0渐进稳定，当μ＞0存在渐进稳定极限环；

3）当c＜0和a＞0时，平衡点对μ＞0渐进稳定，对μ＜0不稳定，当μ＞0存在不稳定极限环；

4）当c＜0和a＜0时，平衡点对μ＞0渐进稳定，对μ＜0不稳定，当μ＜0存在渐进稳定极限环。

3 火箭弹非线性角运动计算分析

根据外弹道学的理论［13］，尾翼弹的飞行不稳定主要是由非线性马格努斯力矩造成的。高原大射角射击时，火箭弹主动段后弹道上空气密度明显降低，导致马格努斯力矩的影响加剧，从而出现飞行不稳定。降低射角后射击，飞行不稳定现象明显减少，这是因为弹道上空气密度增加，有效抑制了马格努斯效应的不利影响。因此，密度的变化对于马格努斯效应的影响程度较大。本节主要分析考虑立方马格努斯力矩后，选取空气密度作为分岔参数时，某型火箭弹的非线性角运动稳定性的情况。

3.1 角运动方程分岔点计算

将火箭弹参数和所受的力和力矩代入到非线性角运动方程中，求得系统在平衡点O处的雅克比矩阵

它的特征多项式可以写成如下形式:

式中:a4=1；a3=3.0242ρ；a2=0.0875+1 324.944 2ρ+ 3.4063ρ2；a1=17.401 8ρ+2 003.468 8ρ2+1.693 3ρ3；a0=4.387 3×105ρ2+741.855 5ρ3+0.313 5ρ4.

根据四维系统的霍尔维茨判据:稳定条件是特征方程的所有系数为正数，还要Δ3＞0.可以看出角方程雅克比矩阵的特征方程所有系数都为正数，因此只需要判断Δ3的符号。由

计算可得:当ρ＜0.5623时，Δ3＜0，系统平衡点O是不稳定的；ρ＞0.562 3时，Δ3＞0，平衡点O是稳定的。所以，为分岔点，此时高度约为7400 m.

3.2 角运动方程降维

将方程组中的三角函数在零点邻域内进行泰勒展开，忽略三次以上的高阶量，令，进行非奇异线性变换x=py，系统化成

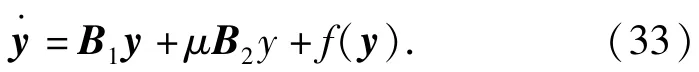
根据中心流形定理，计算其2阶中心流形

忽略3阶以上的项，中心流形上的约化方程为

这样就利用中心流形定理将原四维系统化成了二维系统。

3.3 角运动极限环计算

本节计算密度对极限环的影响，包括两部分:极限环的产生条件及极限环幅值和周期的计算。

3.3.1 角运动极限环产生条件

根据规范形理论，约化后的系统3阶规范形为

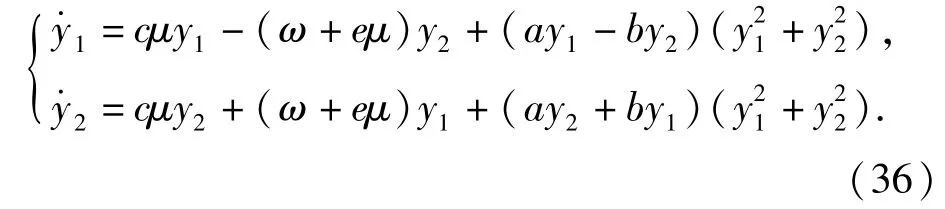
式中:c=-0.378 0；ω=19.454 0；e=-17.165 1；a=-0.002 9；周期T=2π/ω=0.32 s.

引入极坐标变换，得到系统的近似平衡方程0.378 0μr+0.002 9r3=0.其分岔图如图1所示，其中横坐标μ为系统分岔参数，纵坐标r表示Hopf分岔。横轴上实线代表稳定的平衡点，虚线代表不稳定平衡点。

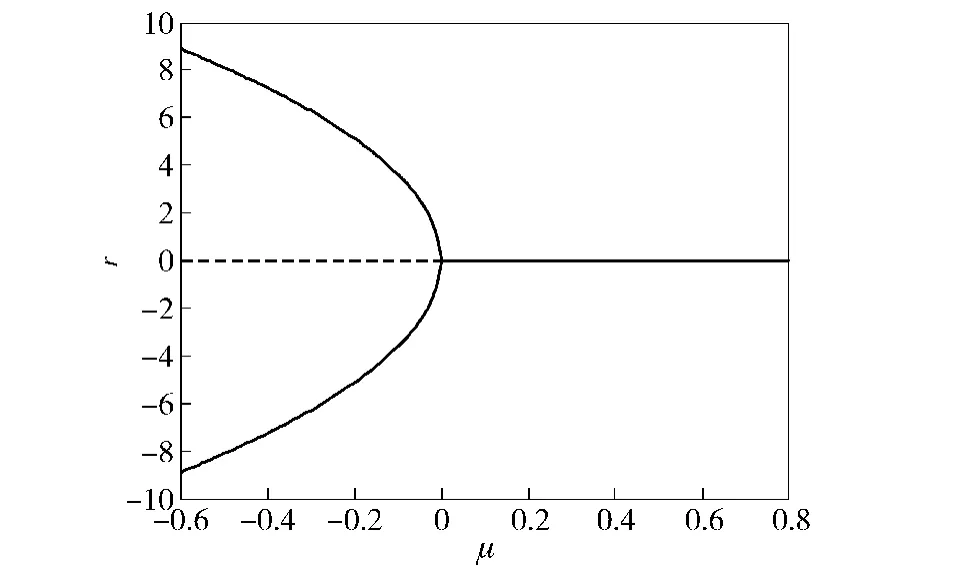
图1 系统Hopf分岔图Fig.1 Hopf bifurcation diagram of system

由分岔图可以看出:当μ＞0时，平衡方程的只有唯一解r=0，此时平衡点稳定；当μ＜0时，平衡

3.3.2 角运动极限环计算

由二维中心流形

则y3、y4表示为

由x=py换回物理坐标得

空气密度ρ分别取0.3 kg/m3、0.4 kg/m3、0.5 kg/m3时，系统的极限环如图2所示。

由图2中可以看出，密度对极限环的幅值影响比较大，当密度减小时，极限环幅值增大。当密度为0.3 kg/m3时，极限环幅值约为13°.

4 数值模拟

当空气密度取ρ=1.2 kg/m3，初始条件为［-1.1° 1.1° 0.6 rad/s -0.6 rad/s］T时角运动如图3所示。

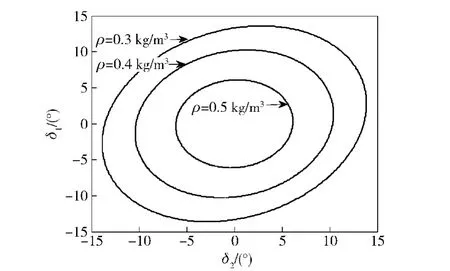
图2 不同密度时的角运动极限环Fig.2 Limit cycles of angular motion for different densities

图3 ρ=1.2 kg/m3时角运动轨迹相图Fig.3 Trajectory diagram of angular motion for ρ=1.2 kg/m3

当空气密度取ρ=0.3 kg/m3，初始条件为［-8.0° 3.8° 7.5 rad/s -2.1 rad/s］T时角运动如图4所示。

图4 ρ=0.3 kg/m3时角运动轨迹相图Fig.4 Trajectory diagram of angular motion for ρ=0.3 kg/m3

从图3和图4中可以看出:在初始值给定的情况下，ρ=1.2 kg/m3时，系统的运动为趋近于平衡点；ρ=0.3 kg/m3时，系统的运动为趋近于极限环；当ρ=0.3 kg/m3时，数值模拟得到δ1、δ2的极限环摆幅为13°，和计算相同。

5 结论

本文建立了弹箭非线性角运动方程，给出了弹箭非线性角运动Hopf分岔分析方法。选取某型火箭弹高原射击时的数据，以密度作为分岔参数，计算了角运动的分岔特性。结果显示，密度在0.5623 kg/m3时，角运动开始出现不稳定，此时高度约为7 400 m，这与高原试验中开始出现飞行不稳定的高度基本相同。当密度小于0.562 3 kg/m3时，火箭弹在非线性马格努斯力矩作用下角会出现极限环运动，且极限环的摆幅随着密度的减小而增大。当密度为0.3 kg/m3时，极限环的摆幅约为13°.最后数值模拟验证了分析方法的正确性。本文建立的非线性角运动模型及给出的非线性角运动Hopf分岔分析方法对弹箭的飞行理论、结构设计、试验分析等具有一定的应用价值。

（

）

［1］ 韩子鹏.弹箭外弹道学［M］.北京:北京理工大学出版社，2008. HAN Zi-Peng.Exterior ballistics of shells and rockets［M］.Beijing:Beijing Institute of Technology Press，2008.（in Chinese）

［2］ 李臣明，刘怡昕.大长径比远程弹箭的极限平面摆动及其抑制［J］.系统与仿真学报，2009，21（23）:7390-7393. LI Chen-ming，LIU Yi-xin.Limit plane swing motion and its restraining measure of un-rotary long-range missile with large ratio of length to diameter［J］.Journal of System Simulation，2009，21（23）:7390-7393.（in Chinese）

［3］ 徐明友.高等外弹道学［M］.北京:高等教育出版社，2003. XU Ming-you.Advanced exterior ballistics［M］.Beijing:Higher Education Press，2003.（in Chinese）

［4］ 王华毕，吴甲生.火箭弹锥形运动的数学仿真与抑制措施［J］.北京理工大学学报，2007，27（3）:196-199. WANG Hua-bi，WU Jia-sheng.Coning motion of rockets，its numerical simulation and restraint［J］.Transactions of Beijing Institute of Technology，2007，27（3）:196-199.（in Chinese）

［5］ 王华毕，吴甲生.火箭弹锥形运动稳定性分析［J］.兵工学报，2008，29（5）:562-566. WANG Hua-bi，WU Jia-sheng.The coning motion stability analysis of rocket［J］.Acta Armamentarii，2008，29（5）:562-566.（in Chinese）

［6］ 闫晓勇，杨树兴，张成.基于章动运动理论的火箭弹锥形运动稳定性分析［J］.兵工学报，2009，30（10）:1291-1296. YAN Xiao-yong，YANG Shu-xing，ZHANG Cheng.Analysis of stability for coning motion of rockets based on theory of nutation movement［J］.Acta Armamentarii，2009，30（10）:1291-1296.（in Chinese）

［7］ 李克勇，赵良玉，周伟.一类旋转弹在高空中的锥形运动稳定性［J］.动力学与控制学报，2012，10（3）:239-243. LI Ke-yong，ZHAO Liang-yu，ZHOU Wei.Stability for coning motion of a spinning projectile［J］.Journal of Dynamic and Control，2012，10（3）:239～243.（in Chinese）

［8］ Mao X R，Yang S X，Xu Y.Research on the coning motion of wrap around fin projectiles［J］.Canadian Aeronautics and Space Journal，2006，52（3）:119-125.

［9］ 赵良玉，杨树兴.卷弧翼火箭弹圆锥运动收敛速度计算方法［J］.固体火箭技术，2009，32（1）:15-19. ZHAO Liang-yu，YANG Shu-xing.Research on convergence speed of coning motion of wrap around fin rockets［J］.Journal of Solid Rocket Technology，2009，32（1）:15-19.（in Chinese）

［10］ 赵良玉，杨树兴，焦清介.提高卷弧翼火箭弹圆锥运动渐进稳定性的几个方法［J］.固体火箭技术，2010，33（4）:369-372. ZHAO Liang-yu，YANG Shu-xing，JIAO Qing-jie.Several methods for improving asymptotic stability of coning motion of wrap around fin rockets［J］.Journal of Solid Rocket Technology，2010，33（4）:369-372.（in Chinese）

［11］ 任天荣，马建敏.基于陀螺力学的旋转导弹锥形运动分析［J］.宇航学报，2010，31（9）:2082-2087. REN Tian-rong，MA Jian-min.Coning motion analysis of spinning missile based on gyro dynamics［J］.Journal of Astronautics，2010，31（9）:2082-2087.（in Chinese）

［12］ 任天荣，马建敏.旋转弹锥形运动发生区间及频率特性研究［J］.固体火箭技术，2014，37（3）:295-300. REN Tian-rong，MA Jian-min.Research on activating region and frequency characteristics of coning motion for spinning missiles［J］.Journal of Solid Rocket Technology，2014，37（3）:295-300.（in Chinese）

［13］ McCoy R L.Modern exterior ballistics［M］.Atglen，Pennsylvania:Schiffer Publishing Ltd，1999.

［14］ 张琪昌，王洪礼，竺致文，等.分岔与混沌理论及应用［M］.天津:天津大学出版社，2005. ZHANG Qi-chang，WANG Hong-li，ZHU Zhi-wen，et al.Bifurcation and chaos theory and its application［M］.Tianjin:Tianjin University Press，2005.（in Chinese）

［15］ 陆启韶.常微分方程与动力系统［M］.北京:北京航空航天大学出版社，2010. LU Qi-shao.Ordinary differential equations and dynamical systems［M］.Beijing:Beijing University of Aeronautics and Astronautics Press，2010.（in Chinese）

Hopf Bifurcation Analysis of Nonlinear Angular Motion Stability of Projectile

ZHONG Yang-wei，WANG Liang-ming，FU Jian，CHANG Si-jiang
（School of Energy and Power Engineering，Nanjing University of Science and Technology，Nanjing 210094，Jiangsu，China）

In order to analyze the angular motion stability of projectile，the equations of the nonlinear angular motion are derived，and the Hopf bifurcation analysis method of the nonlinear angular motion of projectile is given.Taking a rocket plateau test as an example，the air density is selected as the bifurcation parameter，and the Hurwitz criterion is used to judge the stability of the system.The bifurcation point is determined.Center manifold theory is proposed to reduce the system dimension，and then a three-order normal form of Hopf bifurcation is calculated by plotting the bifurcation diagram.In addition，the effect of the bifurcation parameter on the swing of the limit cycle is analyzed.The numerical simulations show that the bifurcation analysis method can be used to judge the stability of the system correctly and analyze the motion of limit cycle in the system accurately.

ordnance science and technology；nonlinear angular motion；motion stability；Hopf bifurcation

TJ714

A

1000-1093（2015）07-1195-08

10.3969/j.issn.1000-1093.2015.07.007

2014-05-08

国家自然科学基金项目（11402117）

钟扬威（1989—），男，博士研究生。E-mail:zyw_601@163.com；王良明（1963—），男，教授，博士生导师。E-mail:lmwang802@163.com