基于DAWSON法小水线面双体船模型兴波阻力及浮态预报

范井峰李云波

（1.海军驻上海地区舰艇设计研究军事代表室 上海 200011；2.哈尔滨工程大学 哈尔滨 150001）

基于DAWSON法小水线面双体船模型兴波阻力及浮态预报

范井峰1李云波2

（1.海军驻上海地区舰艇设计研究军事代表室 上海 200011；2.哈尔滨工程大学 哈尔滨 150001）

针对小水线面双体船型，基于Dawson法，通过船体局部网格快速划分迭代求解船体模型在不同航速下的兴波阻力、纵倾、升沉以及不同航态下的湿表面面积变化，并给出预报结果与模型试验结果的对比。

DAWSON法；小水线面双体船；兴波阻力；纵倾；升沉

引 言

小水线面双体船（SWATH）优秀的耐波性能已经得到业内共识。例如，“卡玛林诺”号和“海鸥”号小水线面双体船的垂向运动加速度均小于0.1重力加速度；“海鸥”号小水线面双体船4级海况下横摇幅值仅为常规单体船的1/4。 SWATH的耐波性能使其使用效率比单体船高得多［1］，且已广泛用于海洋水文考察船、海上作业试验船、交通艇等。

SWATH由于水线面积较小，航行时纵倾和升沉变化较大，通常SWATH船型均要安装首尾稳定鳍来改善航行时的埋首现象。

本文基于Dawson方法［2-4］，通过船体局部网格［5］快速划分迭代求解船体模型在不同航速下的兴波阻力、纵倾、升沉以及不同航态下的湿表面面积变化，并给出预报结果与模型试验结果的对比［6］。

1 计算原理

1.1 兴波阻力基本理论与方法

取随船坐标系，坐标原点位于水平面上，见下页图1。

图1 坐标系示意图

假设流体理想，流动定常，无限水深，船舶兴波为微幅波。流场速度势ψ分解为无自由面影响的重叠模速度势?和考虑自由液面作用的扰动速度势φ，即

速度势均满足无穷远处趋于零的远方辐射条件。考虑到?关于静水面对称，则

将自由面条件（5）分别在z=ζ和z=0上速度势展开，并假设????，忽略?的非线性项，可得简化的自由面边界条件

式中：l为重叠模流线方向。

船体受到的兴波阻力Rw、兴波阻力系数Cw、升力Fz、力矩Mz表示为：

1.2 网格处理

为了在较大傅汝德数范围内获得较准确和光滑而真实的兴波波形，将自由面网格沿纵向从船首向远前方、船尾向后方呈辐射状网格长度按比例递增。横向网格尺度按比例向外递增，波形变化较大区域，采用较密集的均匀网格宽度。

2 计算结果与试验结果对比

本文主要对正常排水量下的船舶阻力及航行姿态进行分析。该船模主尺度见表1。

表1 船舶主尺度

对船模及自由表面进行数值离散，船体表面离散为1 500单元，自由表面单元数为2 300单元。船体表面离散后网格模型如图2。

图2 小水线面双体船网格划分

计算求得的傅汝德数从0.1到0.45共15个速度点的兴波阻力数值计算结果见表2。

表2 小水线面双体船兴波阻力及航态预报结果

图3 -图6给出了计算结果与模型试验结果的对比。

图3 计算兴波阻力系数与试验剩余阻力系数比较

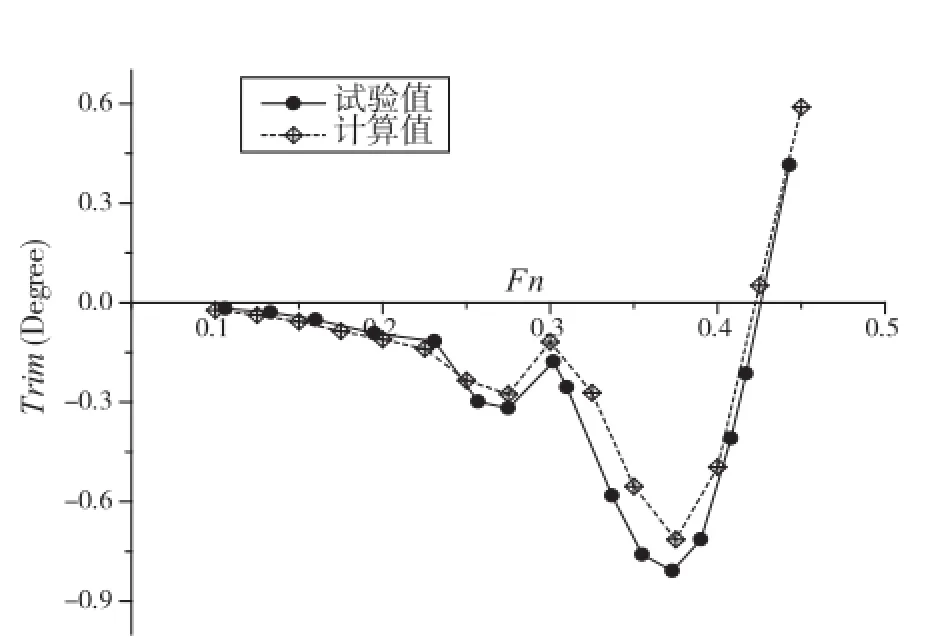
图4 计算纵倾值与试验剩余阻力系数比较

图5 计算升沉值与试验数据比较

图6 计算湿表面面积变化曲线

图3为计算兴波阻力系数与试验剩余阻力系数数据的比较，在计算傅汝德数范围内，该小水线面双体船兴波阻力系数出现明显峰值和谷值，在傅汝德数0.3附近出现明显峰值，在傅汝德数0.35附近出现明显谷值。

图4为计算纵倾值与试验数据比较，在低于傅汝德数0.42时，小水线面双体船均为埋首状态，在0.37附近出现最大埋首状态，在傅汝德数0.3附近纵倾曲线出现拐点，傅汝德数超过0.42后出现抬首现象。从该曲线可知，小水线面双体船航行纵倾随航速变化出现明显的波动情况。

图5为计算升沉值与试验数据比较，从图中可知，小水线面双体船航行时船中吃水都会变大，即出现下沉情况。

从图4、图5可以看出，数值模拟的升沉、纵倾值与试验值的变化趋势相符。纵倾值在傅汝德数0.3左右有数值偏差，升沉预报与试验结果吻合较好。

图6为湿表面面积随航速变化的曲线，在计算的航速范围内，湿表面面积随航速增加而增加。

该船型在Fn=0.3时产生的兴波如图7、图8所示。

图7 波形图（Fn=0.3）

图8 波形云图（Fn=0.3）

从图中可见，所形成的兴波很好地满足了远方辐射条件，同时波峰、波谷的位置也与实际情况相符。

3 结 论

本文基于DAWSON方法对小水线面双体船兴波阻力、纵倾及升沉进行了预报，并给出船模计算结果与模型试验结果的对比。根据计算结果与模型试验结果对比可见，数值模拟的升沉、纵倾值与试验值的变化趋势相符。纵倾值在傅汝德数0.3左右有数值偏差，升沉预报与试验结果符合较好。湿表面面积随航速变化较大，其随航速增加而增加。

［1］ 黄鼎良.小水线面双体船性能原理［M］.北京： 国防工业出版社，1993.

［2］ Dawson C W. A practical computer method for solving ship-wave problems［C］ . the Second ICNSH，Beckly：University Extension Publication， 1977：30-38.

［3］ 刘应中.船舶兴波阻力理论［M］.北京：国防工业出版社，2001.

［4］ Dawson CW. Calculations with the xyz free surface programfor five ship models［A］.Proceedings of Workshop on Ship Wave-Resistance Computations［C］//David W.Taylor Naval Ship Research and Development Center，Bethesda，MD，1979.

［5］ Hess J L， SmithAMO.Calculation of non-lifting potential flowabout arbitrary three-dimensional bodies［J］. Journal of Ship Research，1964（2）： 22-44.

［6］ 蔡新功.基于Michell理论的多体船阻力计算［J］.船舶，2007（2）：5-9.

Prediction of wave-making resistance and fl oating state of SWATH based on DAWSON method

FAN Jing-feng1LI Yun-bo2
(1. Representative Offi ce of Naval Warship Design & Research, Shanghai 200011, China; 2. Harbin Engineering University, Harbin 150001, China)

A small waterplane area twin hull （SWATH） is investigated based on Dawson method. It iteratively solves the wave-making resistance， trim， sinkage and the wetted surface area under the diff erent fl oating states of the ship model at diff erent speeds through the quick division of the local ship grid， and the prediction results are compared with the model test results.

DAWSON method； SWATH； wave-making resistance； trim； sinkage

U661.31

A

1001-9855（2015）06-0020-04

2015-01-13；

2015-03-18

范井峰（1978-），男，工程师，研究方向：舰船设计审查。

李云波（1968-），女，博士，教授，研究方向：船舶水动力性能。