集装箱船型线多速度点的数值优化

陈红梅 冯 毅 于 海 王金宝

（中国船舶及海洋工程设计研究院 上海 200011）

集装箱船型线多速度点的数值优化

陈红梅 冯 毅 于 海 王金宝

（中国船舶及海洋工程设计研究院 上海 200011）

为获得更优化的EEDI指数，集装箱船需要基于营运范围内的型线优化，以实现油耗降低。文章以某集装箱船为研究对象，利用数值优化集成系统，采用最优化技术、曲面自由变形技术（FFD）和计算流体力学技术（CFD），对船体首部型线进行优化。数值计算表明：所得到的优化型线高速段功率略有增加、低速段功率显著降低。

数值优化集成系统；最优化技术；自由变形技术；计算流体力学技术

引 言

降低船舶的设计航速，将导致所需推进功率的相应降低［1］。集装箱船的航速曾一度为25 kn左右（高速段），然而，自2008年开始，部分集装箱船的平均航速降至20 kn左右（低速段）甚至更低，以获得更优化的EEDI指数。这催生出新的集装箱船设计理念，即在尽量保持高速段的阻力性能之下，追求低速段的阻力性能。

本文采用数值优化集成系统，应用最优化技术、曲面参数化和自由变形技术，对集装箱船的首部，针对多速度点下的兴波阻力系数进行多目标优化设计，并对原型方案和优化方案进行总阻力的数值验证，证实本文的多点数值优化方法比较成功。

1 数值优化集成系统

文中采用的数值优化集成系统［2］主要由优化平台软件OPTIMUS、曲面变形软件DEP-Morpher、船舶性能评估CFD软件SHIPFLOW组成。采用该集成系统对船体曲面的水动力性能进行优化时，利用OPTIMUS软件中的最优化技术，对目标函数进行寻优［3］；利用DEP-Morpher中的参数化技术和自由变形技术，对曲面进行改型和自动光顺［4］；利用SHIPFLOW软件中的势流求解器，对目标函数进行数值预报［5］。

对于本文建立的数值优化集成系统，通过优化软件平台，将船舶流体力学数值计算软件和曲面变形软件无缝连接，实现船型自动优化。从而可以无需人为干预，进行较大量的方案考察，找到符合工程要求的较优化船型。

所建的优化平台主要工作流程如图1所示。

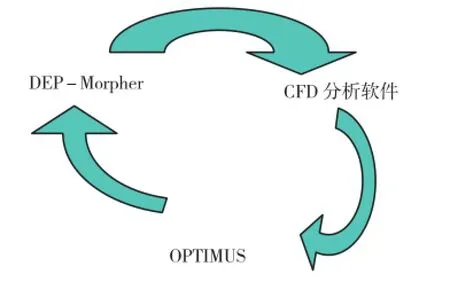
图1 工作流程图

2 集装箱船首部型线多速度点的优化

2.1 优化任务要求

众所周知，不同的球首设计方案有自己的航速适用范围，例如，适用于低速段的球首，在高速段阻力性能可能变差，故而球首的设计优化往往是针对设计点进行，兼顾多速度点的性能，使型线设计具有一定难度。

本文优化设计的对象为万箱级集装箱船。对原方案A在满载吃水状态下（13 m），采用FLUENT软件就3个速度点，即14 kn、18 kn和23 kn，进行数值计算评估，评估结果显示，中低速远不能满足技术指标要求，高速点还稍有裕度。

本文采用数值优化集成系统，在方案A基础上进行优化，对上述吃水状态下不同速度的兴波阻力系数进行数值自动优化，期望所有考核速度点阻力均减小，尤其需要加大低速段的阻力减小幅度。这是一项多速度点下对首部型线的多目标优化设计任务，根据要求，本次的改型范围限制在全船长的首部两站，主要对球首进行改型设计。

2.2 首部多速度点优化设计

2.2.1 建立优化问题的数值模型

（1）目标函数

本次优化的目标为设计吃水下三个不同速度时，兴波阻力系数Cw最小，见表1。

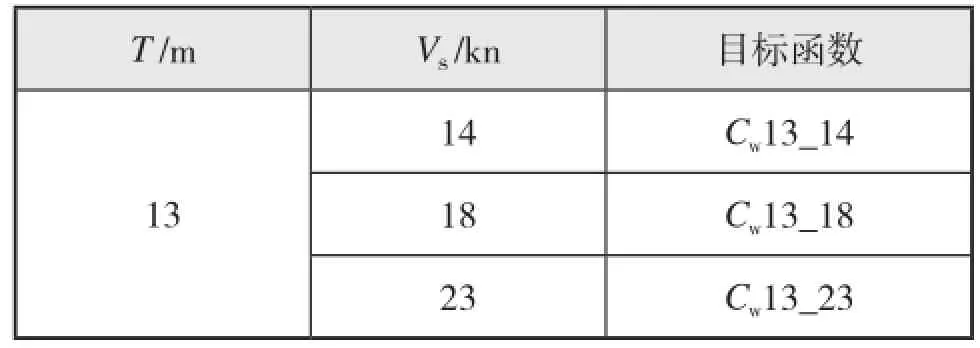
表1 不同工况

（2）曲面参数化及定义设计变量

优化是一个复杂的计算求解过程，设计变量的个数是影响优化所需时间的重要因素。在优化过程中采用参数化技术，对船体曲面进行局部或者整体参数化，减小设计变量个数，提高优化效率，而不明显影响优化效果［6-8］。

由于优化对象速度变化范围较大，不同速度下兴波阻力值较优的船型一般差别很大。为了解决船型变化太大导致船体曲面变形时可能不光顺的问题，在DEP-Morpher中采用FFD技术对首部参数化时，所有的设计变量均设置在一个控制体内［9］，如图2所示。

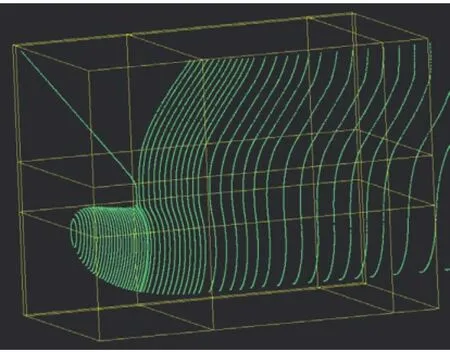
图2 控制体

在控制体的顶点上分别选取适当的控制点，对球首的主要参数进行参数化，即以控制点沿x轴、y轴、z轴的位置变动量dx、dz、dy为设计变量，分别对应球首三个特征参数，即球首的长度、高度、宽度的变化。图3所示为沿Y轴移动控制点实现球首宽度的变化。

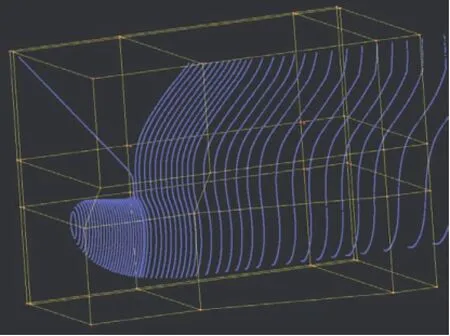
图3 移动控制点改变球首的宽度

（3）约束条件

在确定设计变量的变化范围时，首先根据经验分析不同速度点时球首的特征参数最佳值。然后在DEP-Morpher中，在最佳值两侧，改变设计变量的值，确定设计变量的变化范围，见表2。表中负值表示球首长度、宽度以及高度对应减小，正值则反之。

表2 设计变量的变化范围

2.2.2 优化设计结果及其分析

以SHIPFLOW为计算分析软件，采用曲面变形网格软件DEP-Morpher进行曲面变形，在OPTIMUS中建立的流程图见图4。

图4 流程图

根据建立的流程图，首先采用Latin-Hypercube方法，进行试验设计（DOE），共计算100个方案。试验设计，既可独立进行一定程度的优化工作，也可看作进一步数值优化工作必要的前处理。本次优化设计的设计变量为3个，但样本点的数量远超设计变量。而从试验设计得到的结果，可以指导后续优化方案的设定，有可能大大提高优化效率，而不明显影响优化效果。

在作进一步优化时，采用全局准则多目标优化方法，目标为不同工况状态下兴波阻力系数最小。在全局准则多目标优化方法中，目标函数的排序不同，优先程度也不同，权重与目标的排序有关，排序第一的目标函数，权重较大，排序最后的目标函数，权重最小。根据优化要求，主要减小低速段的兴波阻力系数，所以3个目标函数的排序为Cw13_14、Cw13_18、Cw13_23。

同时，根据试验设计（DOE）计算结果中各速度点的兴波阻力系数较优的设计变量，构建出组合方案，作为本次优化的起始点。

这样，多目标优化时得到最优方案B，设计变量值的比较见表3，首部型线比较见图5。原方案A和最优方案B目标函数（兴波阻力系数）比较见表4。

表3 不同方案设计变量值的比较

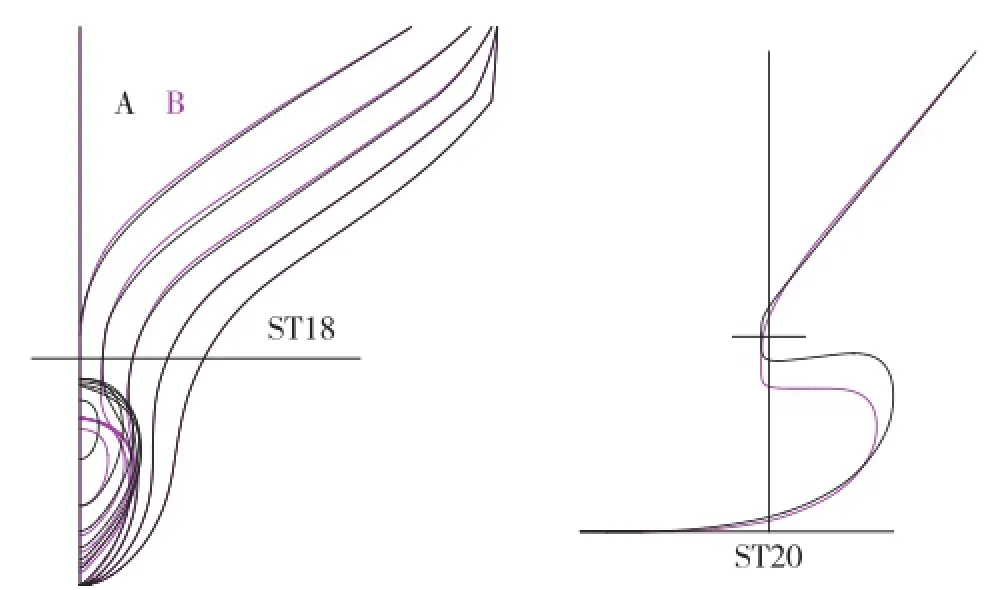
图5 最优方案（B）与方案（A）首部比较

表4 最优方案（B）和原始方案（A）目标函数值的相对差异

从表3和图5可知，最优方案B与方案A相比，球首的主要参数长度、宽度、高度均有减小。根据球首的减阻机理，该球首可对低速段船体兴起的波浪产生有利干扰。从表4可见，在低速段兴波阻力值有较好改善，而高速段阻力有所增加。整体上取得了比方案A更优的效果。

3 优化结果的数值验证［10］

在此次优化工作中，仅以不同方案的兴波阻力为目标进行优选，对总阻力并未进行考核。因此，对原型方案A和最优方案B，有必要采用算法更为严谨的流场计算软件进行数值验证。

本文采用FLUENT软件，通过求解RANS方程，以总阻力为目标进行数值验证。对不同方案，所有的边界条件和网格划分方法均相同。2个方案的实船总阻力结果比较见表5。

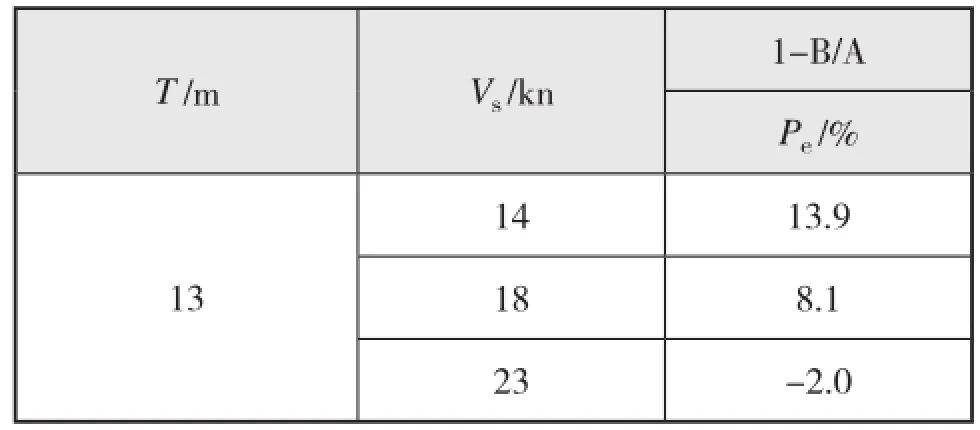
表5 最优方案（B）和原始方案（A）实船总阻力的相对差异

从表5比较可知，在不同速度下，计算所显示的B相对A的优化效果与自动优化结果定性一致，即低速段的阻力性能更优，而高速段的阻力性能略有降低。

不同方案、不同速度点的波形比较见下页图6。

比较两个方案的波型：速度14 kn和18 kn，A方案球首偏大，产生的扰动过强，对该速度范围减阻不利；B方案球首正上方的水面提升和船体首部的波形有明显改善，球首对船体的兴波形成有利干扰。速度23 kn，A方案的首部波形比B方案好，B方案在该速度点首波峰和波谷均增大，阻力性能变差。可见，球首小对低速较有利，但是速度增高，阻力性能就会变差。粘性计算与势流计算结果一致。

图6 波型

4 结 论

本文利用建立的数值优化集成系统，采用最优化技术、FFD参数化技术和CFD技术，对万箱级集装箱船的首部型线进行不同速度点的兴波阻力优化，并进行总阻力的数值验证，结果表明采用数值优化系统的首部型线自动优化方法切实可行、卓有成效，可应用于船型优化。

多目标优化设计问题，相对于凭借经验的人工改型，具有较强的挑战性。本文采用数值优化集成系统进行船型优化，获得较理想的优化效果，说明采用最优化技术在一定程度上可以超越人的经验，寻找到更优的船型设计方案，并可能带来创新的船型设计思路。对本文的优化方案，后期会进行模型试验的验证，不断完善数值优化集成系统的功能。

［ 1 ］ 诸琳.对新造船能效设计指数的思考［J］.船舶工程，2012（1）：29-31.

［ 2 ］ 陈红梅，蒋技赟.船舶水动力性能的数值优化集成系统研究［J］.船舶，2012（2）：21-24.

［ 3 ］ Optimus Revision 10 Theoretical Background［M］. 2011：25-26.

［ 4 ］ DEP-morpher 5.0 Help Manual［M］. 2010：405-412.

［ 5 ］ SHIPFLOW 4.7 Help Manual［M］. 2012：117-133.

［ 6 ］ 李胜忠.基于SBD技术的船舶水动力构型优化设计研究［D］.北京：中国舰船研究院博士论文，2012.

［ 7 ］ 赵峰，李胜忠，杨磊，等. 基于CFD 的船型优化设计研究进展综述.船舶力学，2010（7）：812-821.

［ 8 ］ 冯佰威，刘祖源，常海超，等.船舶CAD/CFD一体化设计过程集成技术研究［J］.武汉理工大学学报（交通科学与工程版），2010（4）：649-651.

［ 9 ］ 陈红梅.数值优化集成系统在船舶水动力性能设计中的应用.［D］.上海：中国船舶及海洋工程设计研究院，2013：51-52.

［10］ 万箱集装箱船优化设计和CFD计算报告［R］.中国船舶及海洋工程设计研究院，2015.

Numerical optimization of hull lines of container ship
at multi-speed points

CHEN Hong-mei FENG Yi YU Hai WANG Jin-bao
(Marine Design & Research Institute of China, Shanghai 200011, China)

The hull form of a container ship is optimized during its operation to attain optimal EEDI index，resulting in the reduction of oil consumption. The bow of a container ship is optimized based on the numerical optimization integration system， which incorporates the optimization technique， the free-form deformation （FFD）technique， and the computational fl uid dynamics （CFD） technique. The numerical results show that the power of the optimized hull line increases slightly at high speed， but decrease remarkably at low speed.

numerical optimization integration system； optimization technique； FFD technique； CFD technique

U661.31+2

A

1001-9855（2015）06-0008-05

2015-03-31

陈红梅（1977-），女，博士，高级工程师，研究方向：船舶型浅自动优化。

冯 毅（1982-），男，硕士，高级工程师，研究方向：船舶快速性。

于 海（1980-），男，硕士，高级工程师，研究方向：船舶CFD计算。

王金宝（1969-），男，博士，研究员，研究方向：船舶CFD研究。