风雨激振中斜拉索表面水线运动的三维数值模拟

王剑 毕继红 关健 乔浩玥 邵倩 周燕 管青海

摘要：基于滑移理论推导三维水膜运动方程，重点考虑斜拉索表面水膜形态变化对风压力系数和风摩擦力系数的影响，建立模拟风雨条件下三维节段斜拉索表面水膜形态变化的理论模型。在此基础上推导出三维节段斜拉索气动力的计算公式，研究水线运动对拉索气动力及其振动响应的影响。结果表明：应用三维滑移理论模型数值模拟得到的拉索表面上下水线的位置、形态与风洞试验结果相近;发生风雨激振时斜拉索的顺风向振幅明显小于横风向振幅;水线沿拉索环向与轴向运动使得水膜形态发生低频周期性变化，导致拉索气动升力与阻力的同频周期性变化，从而引起拉索的大幅度振动，产生风雨激振现象。

关键词：风雨激振;斜拉索;三维模型;滑移理论;水线

中图分类号：TU312+。1;U443.38文献标志码：A 文章编号：1004-4523（2020）03-0559-11

DOI：10.16385/i.cnki.issn.1004-4523.2020.03.015

引言

斜拉桥拉索由于具有质量轻、刚度小和阻尼小的特点，在风雨共同作用下，极易发生大幅度的低频振动，即风雨激振现象。国内外诸多学者通过一系列的现场观测和风洞试验研究，发现斜拉索表面上水线的形成与振荡是风雨激振现象的主要标志和关键影响因素。为此，科研人员一方面采用人工水线风洞试验测量水线对拉索气动性能的影响，另一方面通过人工降雨风洞试验并采用各种测量方式观测水线的运动特性。

由于水线尺寸较小，形态变化多种多样，仅仅依靠风洞试验研究很难全面掌握水线运动与斜拉索振动间的内在联系，因此有必要采用数值模拟方法进行相应的研究。自2007年Lemaitre等首次应用滑移理论研究水平静止拉索表面上的水膜形态变化并模拟水线的形成以来，经过Taylor等、许林汕等、毕继红和王剑等的不断完善，滑移理论逐渐发展成为数值模拟水线运动的重要方法。

目前，滑移理论的研究还主要集中于二维断面模型研究，而斜拉索的风雨激振是复杂的三维问题，应考虑水的轴向流动和气流的轴向流动。对此，Bi等基于滑移理论推导出了考虑拉索振动和气流作用的三维节段拉索表面的水膜运动方程，将拉索振动响应作为已知条件带入水膜运动方程，重点研究拉索振动对水线运动的影响规律。众所周知，水线运动受重力、气流作用和拉索振动三个方面共同作用，而水膜形态变化又会对气流作用产生影响。对此，本文应用已建立的三维水膜运动方程，忽略拉索振动对水膜形态的影响，而重点考虑斜拉索表面水膜形态变化对风压力系数和风摩擦力系数的影响，建立模拟风雨条件下三维节段斜拉索表面水膜形态变化的理论模型;在此基础上推导出三维节段斜拉索气动力的计算公式，研究水线运动对拉索升力、阻力的影响;而后将拉索气动力施加到斜拉索模型上得到斜拉索的振动响应;与已有的风洞试验及数值模拟结果进行比对验证，揭示风雨激振现象的产生机理。相比于以往的基于滑移理论的研究，本文突破了二维断面模型的限制，建立的三维模型能够考虑水线沿斜拉索的轴向流动，更加接近实际，可靠性更高。

1 模型

1.1水膜运动方程

参考文献推导水膜运动方程，半径为R、倾角为a（0°≤a≤90°）的斜拉索节段，受水平方向气流和重力的共同作用，如图1所示，风速为U，风偏角为β（0°≤β≤90°）。

将重力分解，则作用在斜拉索断面内的重力分量g_N和沿斜拉索轴向的重力分量g_z分别为

采用圖2所示的柱坐标系（e_r，e_θ，e_z），根据滑移理论，假设斜拉索表面存在一层连续的水膜，斜拉索节段任一断面（A-A）上的水膜受力如图3所示。水膜内任一点的坐标为（r，θ，z），R≤r≤R+h，h为水膜厚度;速度u表示为分量形式u=u_rr_r+u_θe_θ十u_ze_r，则三维Navier-Stokcs公式可写为

方程的边界条件包括：

（1）位移边界条件：水膜在底面（r-R）处相对于斜拉索表面静止，即

式中 t为时间，u为水的动力黏度系数，r为水在空气中的表面张力系数（r，u与θ无关），δ和δ_g分别为水膜和空气的应力张量，I为单位向量，n为水膜与空气交界处的法向向量，K为水膜表面的曲率（K=-▽·n），p为水膜内的压强;p_g为水膜表面所受空气压力，τ_g为空气黏滞力张量。

（3）自由边界条件：

水膜在与空气交界面F（r，θ，Z，t）=R+h（θ，z，t）-r=0处满足

将边界条件带人式（4）并进行无量纲处理，得到无量纲的三维水膜运动方程

1.2 拉索气动力与拉索振动方程

斜拉索任一断面（A-A）的受力如图4所示，图中F_r（θ，z）和F_θ（θ，Z）分别为水膜底面（r=R）处的法向力和切向力。水膜底面（r=R）处的应力张量为：

整个三维刚性斜拉索节段的气动阻力和升力分别为

2 数值求解

2.1 风压力系数C_p与风摩擦力系数C_f

在滑移理论中，气流对水膜形态变化的影响主要体现在水膜运动方程中的风压力系数C_p和风摩擦力系数C_f;而这两个参数又会随着水膜形态的变化而改变，如图5所示。Bi等在应用三维模型研究风雨激振时忽略了水膜形态变化对风压力系数C_p和风摩擦力系数C_f的影响，采用固定参数，具有一定的局限性，无法体现气流与水膜运动之间的相互作用。由于风雨激振中的水线位置和形状多种多样，很难通过风洞试验来确定每一时刻的风压力系数和风摩擦力系数。因此，本文仍采用二维断面模型的相关研究方法，暂时忽略轴向气流的作用，应用COMSOL软件计算每一断面上随时间变化的风压力系数和风摩擦力系数。具体参数设置详见文献。

2.2 数值计算流程

图6显示了采用MATLAB软件数值求解三维水膜运动方程（式（8））及计算拉索气动力（式（11））和拉索振动响应（式（12））的基本流程。

计算C_p和C_f时在COMSOL软件中划分流场网格，此过程需要用到上一时刻的水膜形态，因此在划分网格时需进行参数化处理;水膜运动方程（式（8））为四阶非线性偏微分方程，采用预测-校正差分格式数值求解;依据式（11a）和（11b），在环向和轴向采用二重数值积分方法分别计算拉索的气动阻力F_x和升力F_v;根据拉索振动方程（式（12）），采用四阶Runge-Kutta法求解顺风向与横风向振动响应。

2.3 基本参数

Li等采用超声波测厚系统在人工降雨风洞试验中测量了风雨激振时斜拉索表面的水膜厚度分布，为此后数值研究水膜形态变化提供了实验基础。参照该试验，本文研究选取的基本参数如下：斜拉索半径R=0.05m，自振频率f₀=0.952Hz，风偏角β=22.5°，水膜初始厚度h₀=0.2mm，重力加速度g=9.8m/s²，水密度p=1.0×10³kg/m³，水的运动黏性系数v=1.0×10^-6m²/s，水在空气中的表面张力系数γ=7.2×10^-2N/m，空气密度p_g=1.225kg/m³，空气的运动黏性系数v_g=1.51×10^-5m²/s，斜拉索的线密度p_s=8.57kg/m，阻尼比ξ₀=0.17%。

L1等在试验中发现，倾角α=30°、风偏角β=22.5‘的斜拉索在风速U=6.76-8.04m/s时会发生风雨激振现象，在风速U=7.72m/s时拉索振动尤为明显。故本文在数值计算过程中选择倾角（α=30°、风偏角β=22.5°、风速U=7.72m/s作为计算参数。

根据文献中三维水膜方程的求解精度研究，本文选择0.5m长的三维刚性节段斜拉索作为研究对象;沿斜拉索轴向划分为25个断面，每个断面环向离散为120个点，时间步长为10^-3s;水膜的初始厚度0.1mm。忽略雨滴的影响，参考文献假设三维节段拉索表面的水量守恒，总水量（体积y）不随时间变化，即满足

应用差分法求解水膜运动方程需要水膜在斜拉索表面连续分布，为此设定水膜的最小厚度h_min=0.01mm。

3 数值计算结果

以往的研究表明，风雨激振的形成需要数10s以上的时间，故本文进行了150s的数值计算，并选取120-140s内的计算结果进行研究。

3.1水线的形成

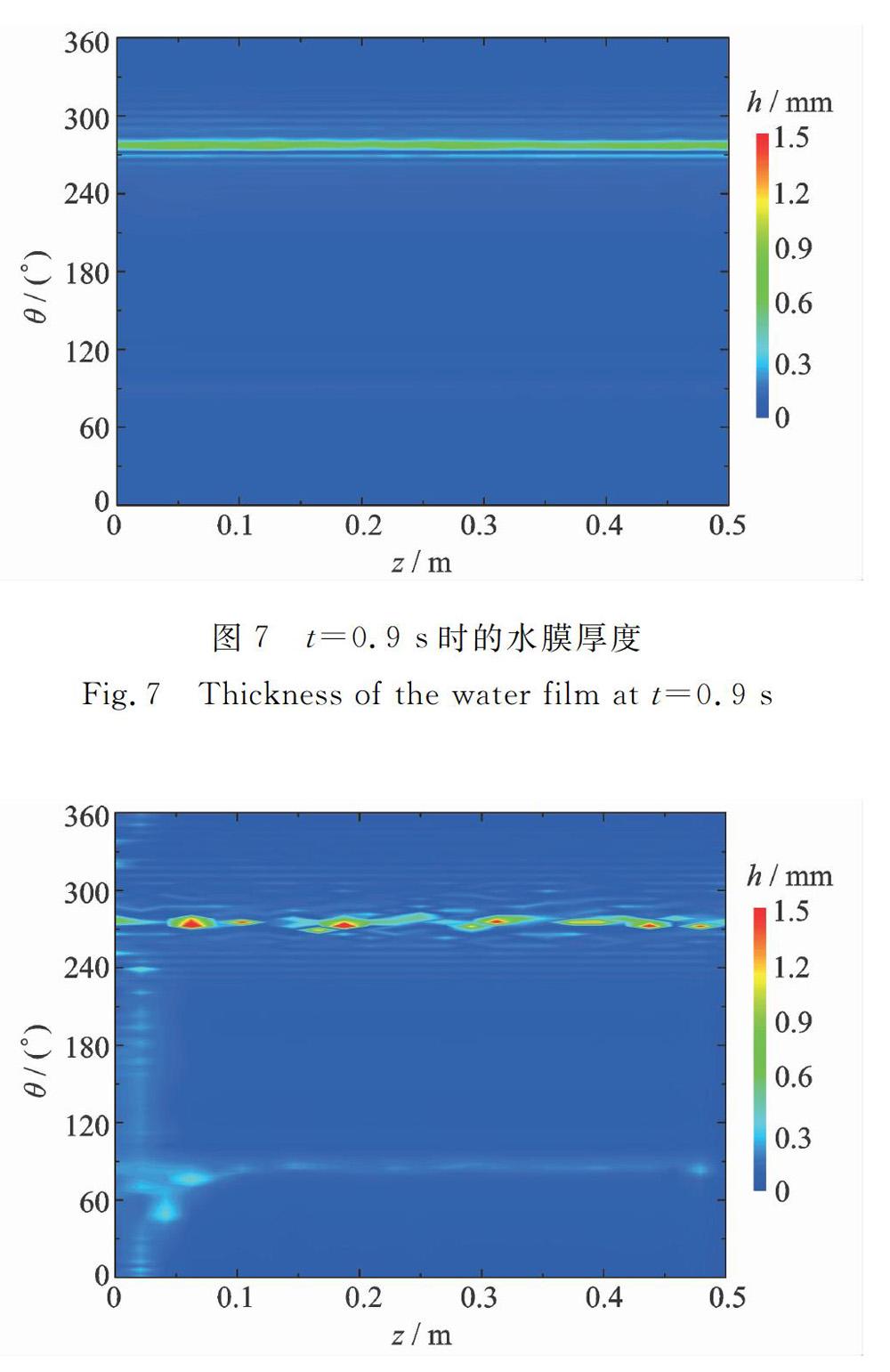
图7显示t=0.9s时拉索表面的水膜厚度分布情况。为便于观察，将三维斜拉索圆柱体展开，横轴表示斜拉索轴向方向，纵轴表示环向方向，图中颜色表示水膜厚度。t=0.9s时，水膜在拉索下方聚集形成下水线，范围在274.5°-280°之间，宽度约为8.8mm，厚度约为0.86mm，此时还未形成明显的上水线。至t=1.4s时，在74°-94°范围内出现了明显的上水线，宽度约为13.9mm，厚度约为0.33mm，如图8所示。

3.2 三维节段斜拉索表面的水膜形态变化

图9-14显示了t=136.0-137.0s时间段内斜拉索表面的水膜厚度分布。下水线位于275°-280°之间，最大厚度约为1.48mm。其位置、形态变化很小，只有厚度在斜拉索轴向方向有明显变化，体现出了气动力和重力共同作用下水的轴向流动。上水线则在55°-90°之间运动，最大厚度约为0.46mm，与风洞试验的观测结果相近。与试验结果不同的是，数值计算结果中上水线的环向运动幅值小于试验结果，其原因主要是计算中未考虑拉索振动对水膜形态变化的影响;此外，数值计算结果中还出现了水滴自上水线位置沿迎风侧下滑并汇合到下水线的现象。产生这一现象的因素除计算中未考虑拉索振动对水膜形态变化的影响外;另一因素可能是应用滑移理论数值模拟风雨激振时无法模拟降雨过程中雨滴下落至斜拉索表面的现象。

3.3 水线的环向运动

图15一18分别表示t=120-140s内Z=0.1m，Z=0.2m，Z=0.3m和Z=0.4m断面处的水膜厚度时程变化。图像横轴表示时间，纵轴表示拉索环向位置，颜色表示水膜厚度。可以看到这四幅图像区别不大。首先，与试验结果相一致，下水线的形态、厚度几乎一致，均稳定在相同范围内（273°-281°）;其次，上水线宽度明显大于下水线，而厚度明显小于下水线，与试验观测结论一致;再次，上水线的运动范围在40°-90°之间，中心位置与试验结果一致而范围略大;最后，这4个断面处均有水从上水线沿迎风侧下滑汇聚至下水线，与二维断面研究的结果一致。

为研究上水线位置处水膜形态变化的运动特性，分别研究Z=0.1m，Z=0.2m，Z=0.3m和Z=0.4m四个断面θ=63°位置处的水膜厚度，如图19-22所示。这四个断面上水线位置处的水膜厚度变化范围均在0.1-0.4mm范围内;对其分别进行频谱分析，发现水膜厚度变化的主频主要有三个：0.253，0.558和0.802Hz，均小于拉索自振频率（0.952Hz），与试验结果有一定区别。对比文献仅考虑拉索振动影响的研究，可以发现产生这一差别的主要原因是本文的计算中未考虑拉索振动的影响，说明拉索振动是导致水线周期性环向振荡的主要因素之一。

由于在計算中出现了水从迎风侧自上水线下滑至下水线的现象，故在上述四个断面上的迎风侧各选取同一位置（θ=9°）的水膜厚度作为研究对象，如图23-26所示。这4个位置处的水膜厚度变化范围在0.1-0.5mm内，略大于上水线位置处的水膜厚度变化幅度。频谱分析显示迎风侧的水膜厚度变化主频与上水线位置处一致，仍为0.253，0.558和0.802Hz。比较这4个断面8个位置的水膜厚度变化，可以发现均有0.802Hz这个频率。

3.4 水线的轴向运动

为研究水线的轴向运动，分别选取t=127-132s内Z=0.30m和Z=0.32m两个相邻断面作为研究对象。由于上水线在40°-90°之间周期性振荡，同时有水周期性的沿迎风侧从上水线下滑汇聚到下水线，故研究上水线（θ=60°和θ=63°）及迎风侧（θ=9°和（θ=12°）的水膜厚度时程变化，如图27所示。Z=0.30m和x=0.32m是数值计算中的两个相邻断面，图27中的对比显示这两个断面的相同环向位置处的水膜厚度变化的幅值基本一致，且迎风侧的变化幅度明显大于上水线位置处。

在同一角度位置，两条水膜厚度时程曲线相近，但水膜最大厚度出现的时间明显不同，有明显的时间差存在，说明水在沿着斜拉索轴向流动;比较同一断面内相邻角度的时程曲线，可以发现水膜厚度变化亦非完全同步。因此，通过三维模型的数值计算可以看出，水线在拉索表面同时沿环向和轴向运动。事实上，水线沿拉索环向和轴向运动是在重力、气流和拉索振动共同作用下形成的，但在本文的研究中，忽略了拉索振动的影响，仅研究重力和气流作用下的水线运动。

3.5 拉索气动力

图28和29分别为t=120-140s内拉索气动升力与阻力的时程变化曲线和频谱分析。两者的变化趋势一致，但升力的变化幅值较大，升力的变化范围是—0.65-2.45N，阻力的变化范围是4.50-6.90n.频谱分析显示升力与阻力的主频均为0.253，0.558和0.802Hz，与上水线位置处的水膜厚度变化频率一致，亦与水线下滑导致的迎风侧水膜厚度变化频率一致。这一现象说明水膜形态变化是导致拉索气动力变化的直接重要因素。

3.6 拉索振动响应

图30所示的t=120-140s内拉索横风向振动响应显示横风向振幅约为0.114m，与风洞试验观测数据基本一致。对比图31显示的顺风向振动的时程曲线，可以发现拉索发生风雨激振时的顺风向振幅约为0.054m，明显小于横风向振幅（0.114m），与Ni等的现场观测结果及以往的二维断面模型研究结论相一致，产生这一现象的主要原因是升力的变化幅值明显大于阻力。由于气动升力有正有负，故拉索横风向振动的平衡位置大致位于原点附近的0.012m处;而阻力一直为正，导致顺风向振动的平衡位置远离原点，大致位于0.142m处。

结合水膜形态研究，可以看出风雨激振是由于水膜形态（厚度）的低频周期性变化导致拉索气动升力与阻力的同频周期性变化，进而引起拉索的大幅度振动。

4 结论

本文基于滑移理论，忽略拉索振动对水膜形态的影响，应用三维水膜运动方程研究重力和气流共同作用下三维斜拉索表面的水膜形态变化;并推导出三维节段斜拉索气动力的计算公式，研究水线运动对拉索升力、阻力及拉索振动的影响，得到下列结论：

（1）应用三维滑移理论模型数值模拟得到的拉索表面上下水线的位置、形态与实验结果相近。

（2）在三维节段模型中考虑水膜形态变化对风压力系数和风摩擦力系数影响，可以较好地模拟水线沿拉索环向与轴向运动。上水线的环向振荡及水线下滑导致上水线附近及迎风侧水膜厚度的周期性变化，二者主频一致，均小于拉索自振频率。

（3）阻力的变化幅度小于升力，导致斜拉索发生风雨激振时的顺风向振幅明显小于横风向振幅，与已有的研究結果相一致。

（4）拉索气动升力与阻力的变化频率与上水线及迎风侧位置处水膜厚度变化频率一致。水膜形态变化是导致拉索气动力变化的直接重要因素。水膜形态周期性变化导致拉索气动力的周期性变化，引发拉索横风向与顺风向的大幅振动，形成风雨激振现象。