一种分布式发电并网变流器测试装置设计方案及实现

李宇飞 王 跃 吴金龙 冯宇鹏

（1. 西安交通大学电气工程学院电力设备电气绝缘国家重点实验室 西安 710049 2. 许继集团有限公司 许昌 461000）

1 引言

基于光伏、风能以及生物能等新能源的分布式发电近年来在电力工业领域受到越来越多的关注。大多数分布式发电系统与电网之间的接口是通过电力电子并网变流器实现的，因此，要保证分布式发电系统的稳定运行，并网变流器的稳定性和抗扰动性就显得至关重要。国家标准“风电场接入电力系统技术规定”[1]以及“光伏发电站接入电力系统技术规定”[2]不仅提出了对新能源分布式发电系统低电压穿越能力的要求，也提出了对电压和频率适应能力的要求，包括电压和频率偏差适应能力、非对称故障适应能力、电网谐波适应能力以及电压波动和闪变适应能力。如果能在并网变流器并网运行之前对并网变流器进行电网适应性测试、并网运行评估，将大大提高分布式发电系统的稳定性。然而，在分布式发电系统实际并网运行时，很难在大电网中直接对变流器进行测试，原因有两点：首先，电网无法按照需求模拟各种非正常工况；其次，直挂电网的测试方式会对电网稳定造成影响。如果使用可编程电源在较低电压等级下对样机进行测试，也只能部分反映真实工况，无法完整复现正常并网运行时高电压、大功率工况带来的问题。

因此，设计一种分布式发电并网变流器测试装置是非常必要的，图1所示为测试系统与分布式发电系统连接示意图，虚线表示不经测试装置的并网运行模式，测试系统以电压源方式运行，模拟不同的电网工况，分布式发电系统对于测试系统来说，可以看作是一个电流源。本文设计的基于级联H桥[3-10]拓扑的波动电压发生装置是开创性的，目前还没有同类型的测试装置可以同时达到以下标准：电压等级可拓展，输出电压幅值频率可调，可高精度地输出频率为 0.5～25Hz和波动幅值为 0～10%基波电压幅值的波动电压，可模拟不平衡度可调节的三相不平衡电网，不平衡度范围为0～10%。而移动式和固定式低电压穿越测试装置已经是一种成熟的工业产品，因此这种测试装置不仅解决了实际电网中并网变流器不易测试的难题，而且填补了分布式发电并网变流器测试的空白，并且输出的测试电压精度很高。此文有望为分布式发电并网变流器测试装置的设计提供一个可参照的标准。本文讨论了测试装置的工作原理，并以在基于所提出测试装置拓扑的“35kV-6MW风机变流器低频扰动测试装置”上进行的现场实验为例，充分证明了这种波动电压发生装置用于分布式发电并网变流器测试的可行性和有效性。此35kV-6MW风机变流器测试装置安装在河北省张家口市“国家能源大型风电并网系统研发（实验）中心”。

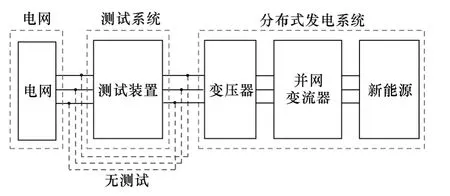
图1 测试系统和分布式发电系统连接示意图Fig.1 Configuration of the testing system and distributed generation system

2 装置结构和工作原理

本文所设计的分布式发电并网变流器测试装置达到了以下性能指标：输出频率为 45～66Hz的额定电压，精度达到0.01Hz，输出幅值为20%到120%额定幅值的电压，误差小于0.1%；输出波动频率为0.5～25Hz和波动幅值为0～10%基波电压幅值的波动电压，并且误差小于0.1%；输出不平衡度范围为0～10%的三相不平衡电压，精度达到0.1%，并且输出三相不平衡电压时，负序电压幅值相位可调；输出额定电压的THD可以达到2%以下。

由图1可以看出，测试系统与分布式发电系统的接口即为测试端口，测试端口为测试电压的输出端口。要保证测试系统与电网的隔离，就必须采用先整流后逆变的拓扑结构。由于测试系统输入端口要接入三相电网，所以输入端的整流器应采用三相变流器。如果采用背靠背式的三相 PWM变流器拓扑，系统很难实现输出波动电压和不平衡电压；如果采用三相PWM整流器整流，再使用单相H桥逆变器独立组成三相电压，虽然从控制角度来说，系统可以实现波动电压和三相不平衡电压，但是单个H桥逆变器的可耐受电压等级有限，无法满足高电压大功率场合。根据这种情况，本文设计的测试装置采用级联H桥拓扑，不仅可以通过本文提出的控制策略生成测试电压，还可以根据分布式发电系统的电压等级，通过改变级联 H桥单元数目来匹配系统电压等级，同时级联H桥变流器的输出电压也具有谐波少，滤波方便，对开关器件耐受电压要求低等优点。图2所示为测试装置主电路拓扑示意图。前级由输入变压器接入电网，后级由输出变压器接入分布式发电系统。在实际装置中，各个系统需要断路器连接，图2中没有画出。输入变压器的二次绕组为 3N组，级联H桥单元数目为N，它由电网和分布式发电系统的电压等级决定，其中各个独立单元的直流母线电压分别由 d-q同步旋转坐标系控制的三相 PWM变流器提供，其控制框图如图 3所示。为了输出测试电压，3个级联H桥变流器被独立控制，分别构成单独一相，并采用三电平移相载波调制策略（Phase-Shifted Carrier PWM,PSCPWM），这种调制策略具有谐波小，输出带宽高，能在较低开关频率下实现较高等效开关频率等优点。这种三电平调制原理如图4所示。图中级联H桥单元个数N=3，PWM 输出电压为假想电平值，载波频率为fc0=2kHz，正弦调制波频率为fm=1kHz，可以看出每个单元输出电压为3电平，总输出电压为2N+1=7电平，等效开关频率fc=2Nfc0=12kHz，提高为原来的6倍。

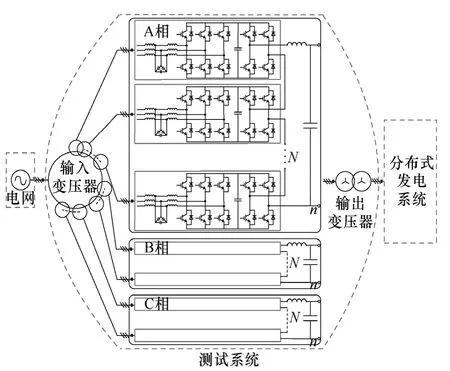
图2 扰动电压发生装置主电路图Fig.2 Main circuit topology of the disturbance voltage generation equipment

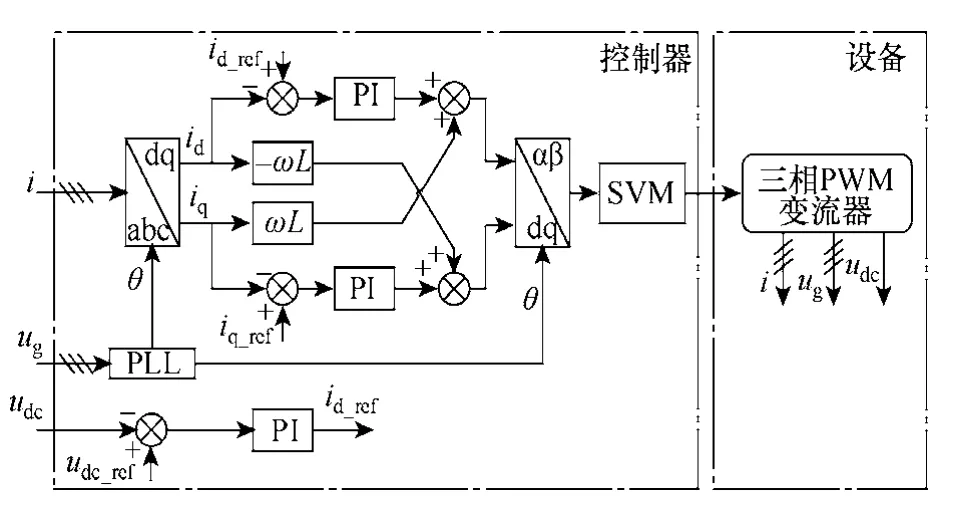
图3 d-q同步旋转坐标系控制框图Fig.3 d-q synchronous rotating frame control

2.1 对称工况电压频率偏差

根据上述讨论，测试装置的输出电压由3个级联H桥变流器组合而成，因此每个级联H桥变流器可以看作是一个独立的单相电压源逆变器。其指令信号表达式为

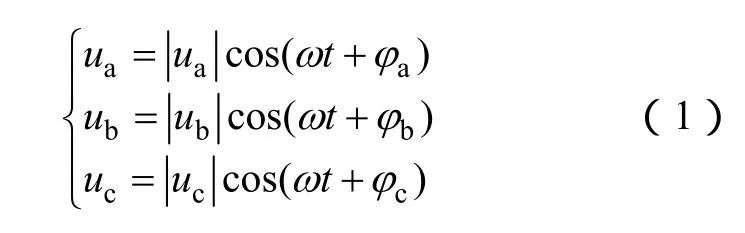
式中，ua、ub和uc分别为三相电压；φa、φb和φc为三相电压初始相位；ω为电压角频率。因此在实际控制中，要实现输出电压的幅值和频率偏差，就可以通过改变式（1）中的幅值和频率来实现。

2.2 非对称电网故障

根据对称向量分解法，三相电压系统可以表示成

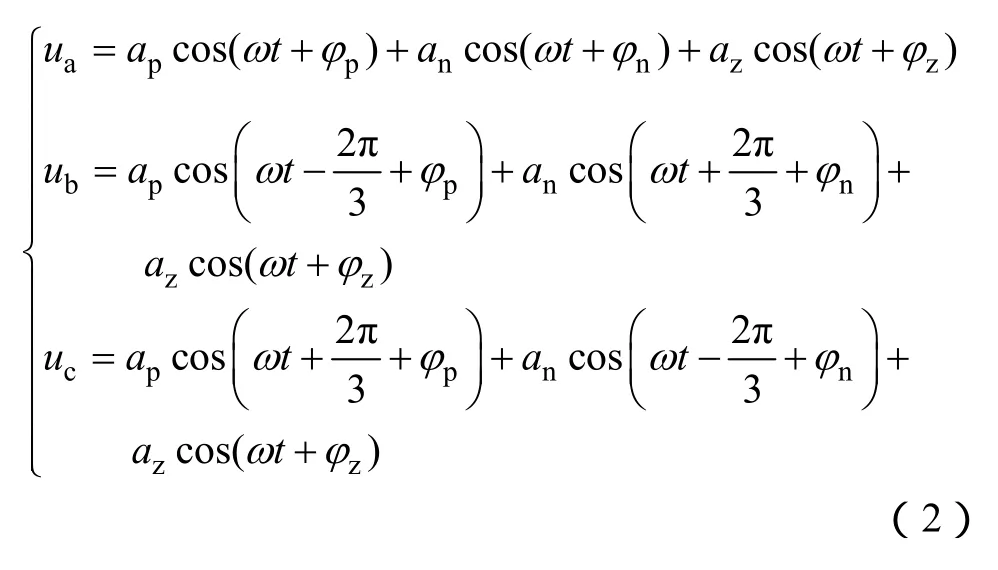
式中，ap、an、az和φp、φn、φz分别为正负零序分量的幅值和相位。将以上方程式变为矩阵形式有

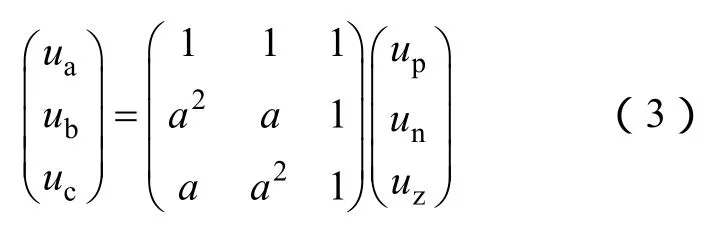
式中，a=ej2π/3。通过以上式子以及正负零序参数，可以计算出 ABC三相指令信号参数。此外，根据IEC 标准[11]以及国家标准[12]，不平衡度定义为m=an/ap。所以，通过已知的不平衡度和正负序分量参数可以很容易得到任意非对称故障的三相系统幅值和相位参考值（ua，ub，uc和φa，φb，φc），非对称故障包括三相电压跌落、相间短路以及两相或者单相接地等电网故障。实际操作中，用户在远端控制室下发不平衡度指令，再选择故障类型，控制器会根据需要自动计算 ABC三相电压幅值相位的参考值。

2.3 波动电压

波动信号的数学表达式为[13]

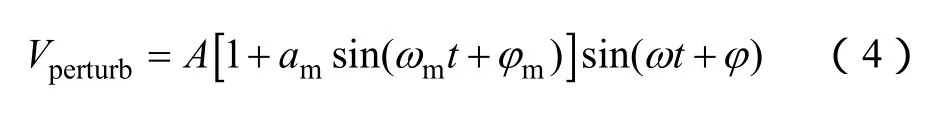
很显然，这可以看作是一个正弦调制的过程。其中，ωm和ω分别为波动角频率和基波角频率；φm和φ分别为调制信号初相位和被调制信号初相位；A为被调制信号幅值；am为波动幅值系数。展开式（4）有

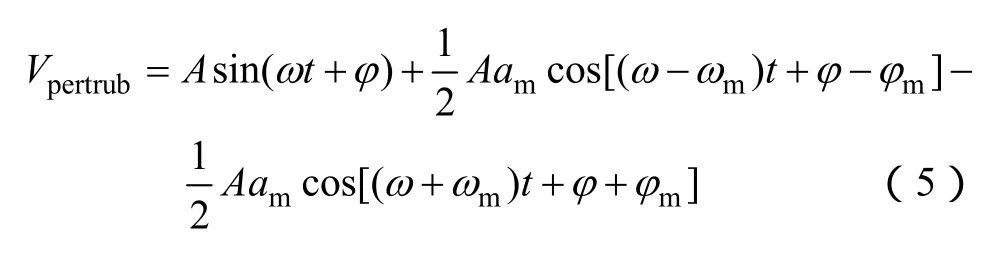
可以看出，Vperturb有 3个频率分量，分别是基波分量和两个与基波频率相差fm的对称分布在基波两边的分量，即低频段分量f-fm和高频段分量f+fm。这实际上就是文献[14]所指出的一对间谐波。文献[14]指出，电压的相对有效值波动（最大有效值和最小有效值的差值，反应了电压的波动程度）与这对间谐波幅值和频率有关，而要保证电压波动程度可控，正是测试装置对分布式发电并网变流器电网电压波动适应能力测试的基本要求。因此测试装置控制系统的目标就是保证输出波动电压的高低频段分量的频率和幅值达到一定精度，这样就能保证波动电压波动程度达标，以便进行并网变流器测试。本文提出一种新型的控制策略-波动有效值反馈控制（Fluctuating RMS Value Feedback Control,FRFC）。FRFC的一个优点是输出波动电压Vperturb具有较高的精度；另一个优点是它的控制结构简单，控制参数容易选取，比较适合高压大功率场合。图5所示为测试装置中级联H变流器的小信号模型，其中Req为变流器内阻，它表征了变流器的内部损耗以及线路损耗；N表示级联单元的个数，控制环节为电压反馈控制。图6所示为FRFC的控制框图，可以看出，uref为波动信号，外环指令信号是实时计算得到的波动信号滑动窗有效值，它也呈现波动特性，滑动窗口长度即为基波电压周期。需要指出的是，在进行对称工况电压频率偏差和非对称电网故障测试时，uref均为正常的正弦指令信号。这样一来，测试装置的所有功能都可以用 FRFC控制策略实现，测试装置就可以实现不同测试功能的在线切换。图中内环使用P调节器而不是PI调节器是为了避免电压传感器零漂移带来的积分饱和效应[15]。图中的黄色框表示指令信号和反馈信号经历了一个共同的过程，即滑动窗有效值计算。滑动窗有效值计算可以看作是一个滤波器，它“滤除”了信号的其他成分，只保留了有效值的波动信息作为指令（波动信号的滑动窗有效值是呈现波动的）。此外，由于 PI调节器在低频段的高增益作用，电压外环的跟踪精度可以得到保障，从而保证了波动信号高低频段分量的幅值精度。

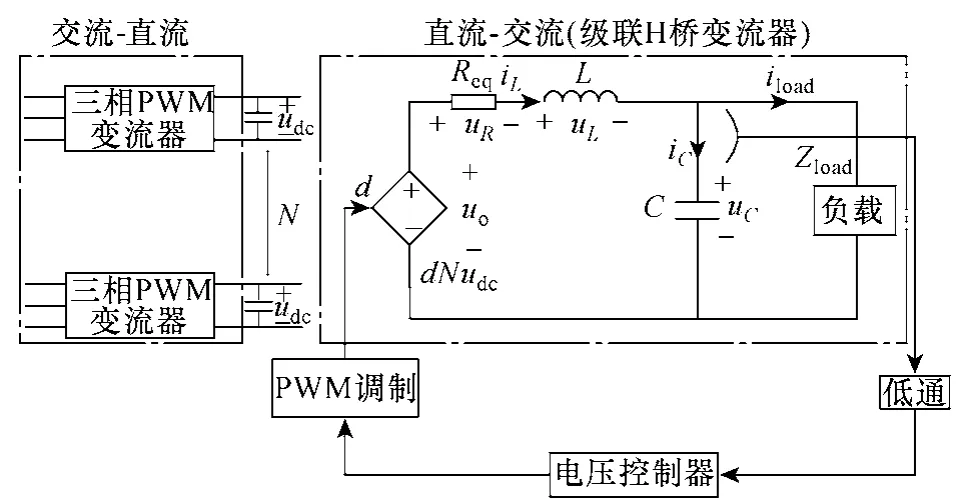
图5 扰动测试系统中级联H桥变流器的小信号模型Fig.5 Small signal model of the CHB converter in disturbance testing system

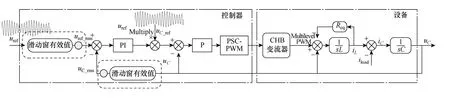
图6 FRFC控制框图Fig.6 Control diagram of the FRFC

3 现场实验结果

所有的实验结果和数据均是在现场的测试装置上得到，为了安全起见，数据均由“Fluke-1760”数据采集系统采集，采样频率为100kHz，并用Matlab进行分析。图7给出了“35kV-6MW风机变流器低频扰动测试装置”变流器组、数据采集系统和断路器图片。图8所示为包含出线和旁路开关的测试系统结构图。实验中，数据采集系统采集电压互感器PT2的电压作为测试系统输出电压，测试时风机发电系统从“35kV测试点母线”接入测试系统。装置的拓扑结构与图2所示相同，其中N=3，电网电压等级为 35kV。可以进行 35kV-6MW 等级的风机测试，满功率相电流可以达到1 176A。装置中LC滤波器电抗L=0.1mH，LC滤波器电容C=90μF；额定输出电压uC=1 700V；额定电流iload=1 176A；满载满功率Pfull=6MW，可以进行 6MW 风机测试；基波频率f=50Hz；扰动电压频率fm=0.5～25Hz；扰动幅值am=0%（pu）～10%（pu）；有效值计算间隔以及采样时间：Ts=1/12 000s。需要指出的是，所有数据均是在测试装置输出侧空载的情况下进行的。系统在空载情况下的稳定域小于带载情况下的稳定域，因此控制参数以满足空载稳定为原则[16]。

图 9所示电压波形为输出频率偏差和幅值偏差，分别是频率为 50Hz，幅值为额定电压幅值的90%和频率为64Hz，幅值为额定电压幅值的A相电压波形。可以看出输出电压的幅值和频率与控制目标是一致的。表1为输出额定电压时三相输出电压的 THD，可以看出三相 THD最大仅为 1.6%。表 2为不平衡度设定值与测量值对比。可以看出测量值与设定值误差非常小。如本文第 2节所说，实际操作中，用户在远端控制室下发不平衡度指令，再选择故障类型，控制器会根据需要自动计算三相电压幅值相位的参考值。本文实验数据均是以A相输出电压为例。图10为测试装置输出的波动电压波形，分别是波动频率 1Hz、波动幅值 9%和波动频率12Hz、波动幅值10%。图11为输出波动电压的FFT分析，可以看出FRFC的结果和表达式（5）是一致的，高低频分量等幅值分布在基波两边，并且幅值与理论值一致。表3为实验得到的不同波动频率和幅值的高低频段幅值，可以看出其幅值和理论之间误差很小。

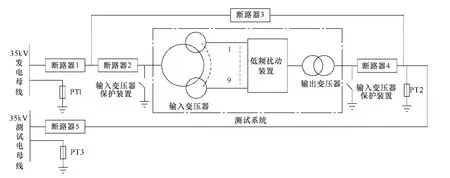
图8 35kV-6MW风机变流器低频扰动测试系统结构图Fig.8 Diagram of the “35 kV-6 MW wind turbine converter testing system” structure

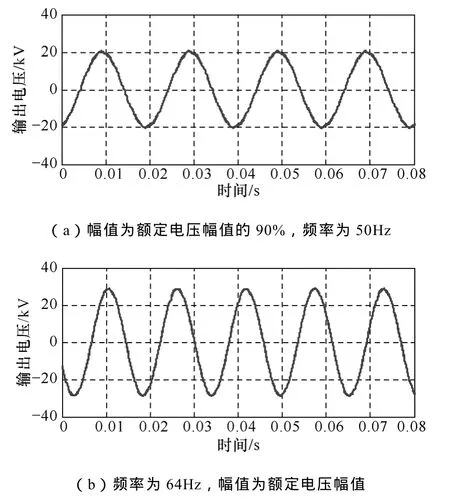
图9 输出电压幅值和频率偏差Fig.9 Amplitude and frequency deviation of the output voltage

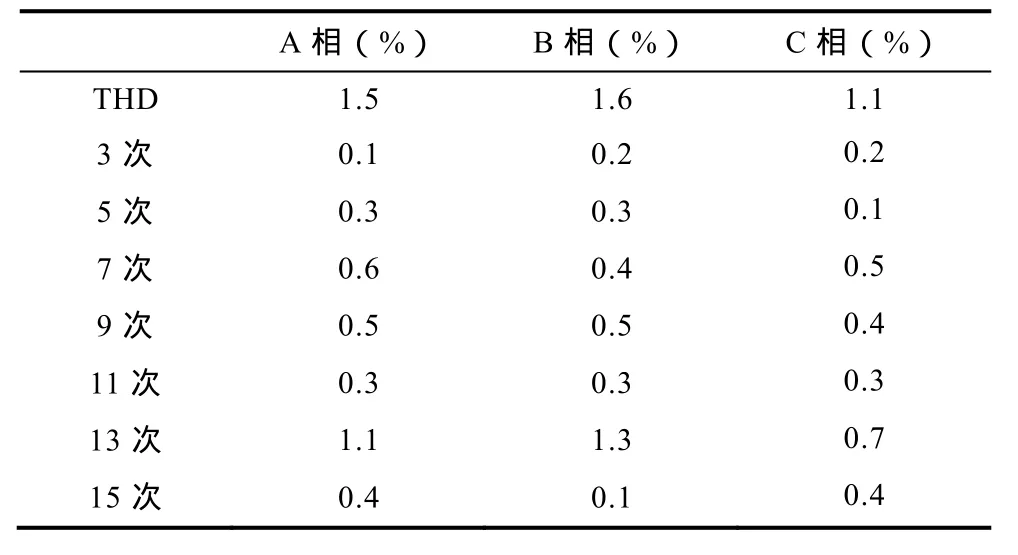
表1 三相输出电压THDTab.1 THD of the three-phase output voltage

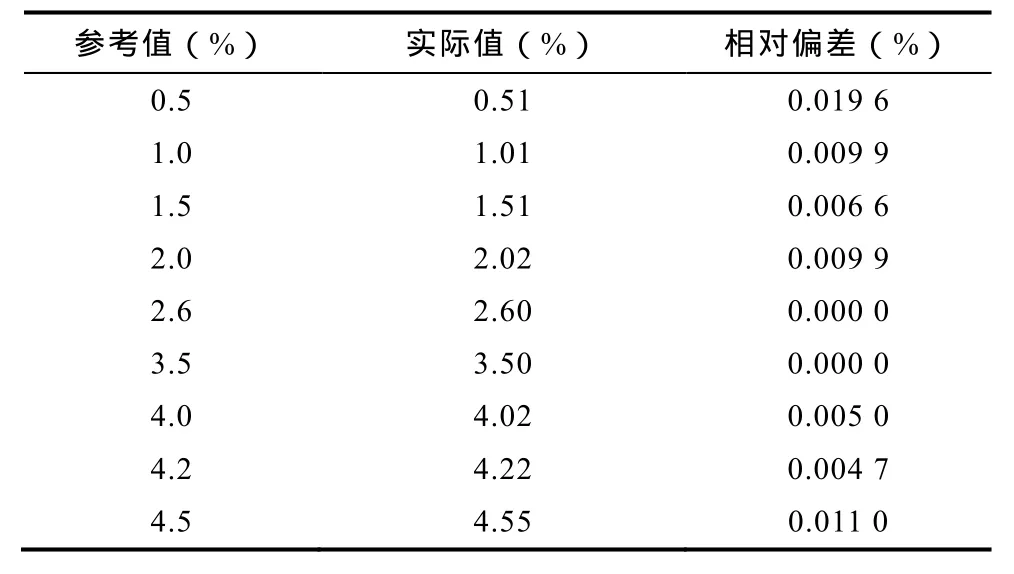
表2 不平衡度参考值与实际值Tab.2 Reference unbalance factor and real unbalance factor

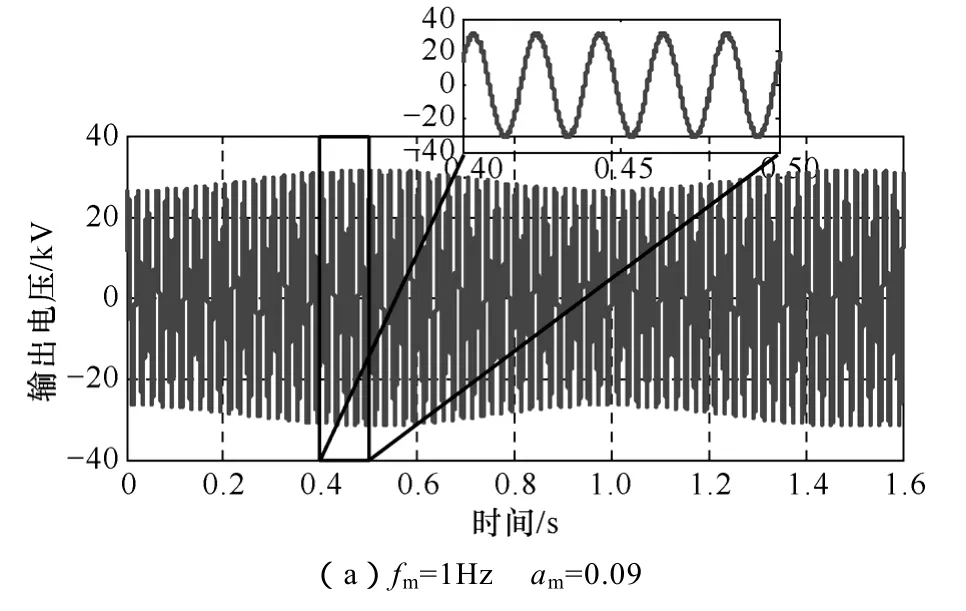
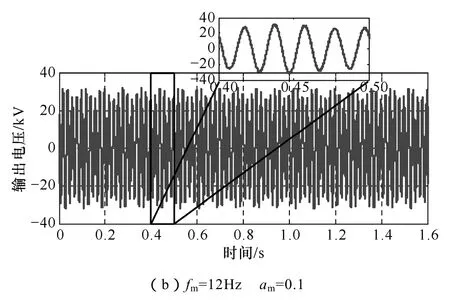
图10 输出扰动电压波形Fig.10 Waveform of fluctuating output voltage

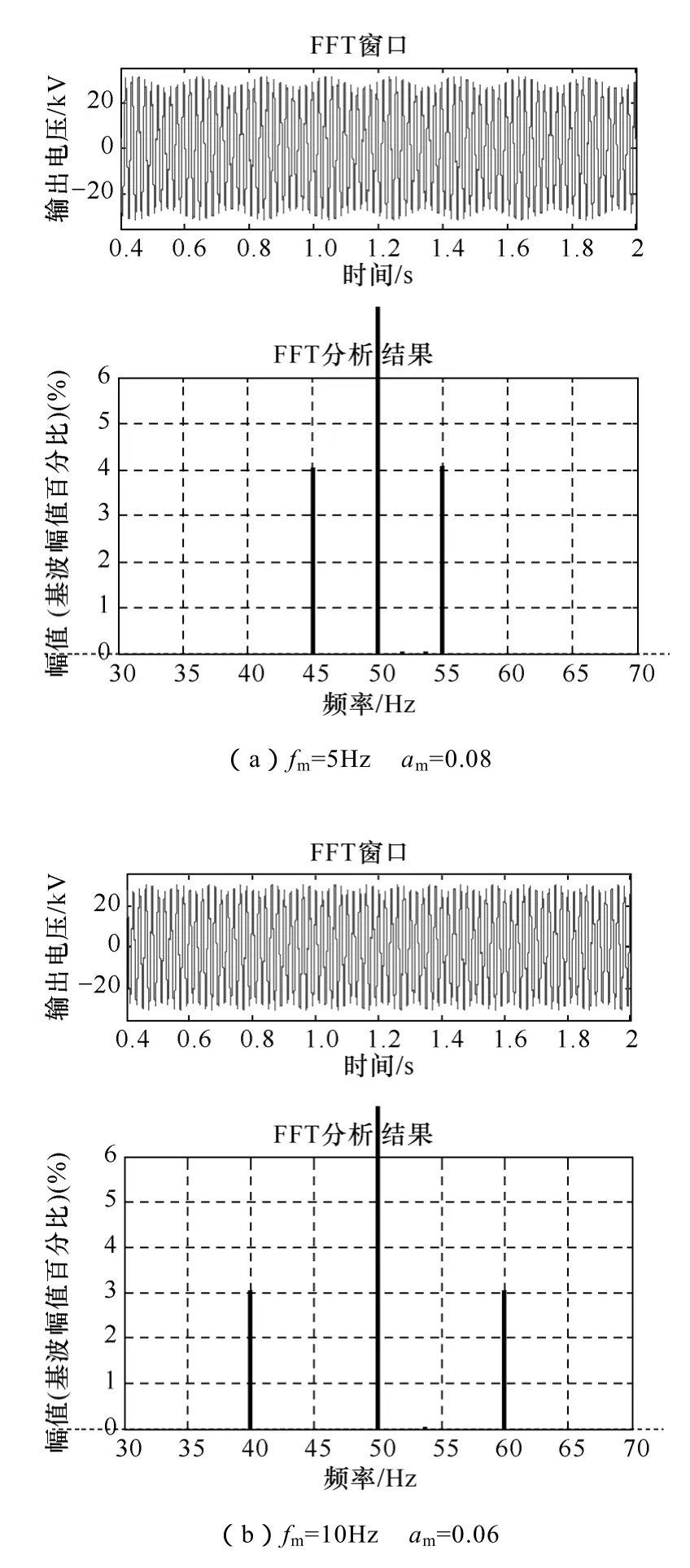
图11 输出扰动电压FFT分析Fig.11 FFT analysis of output fluctuating voltage

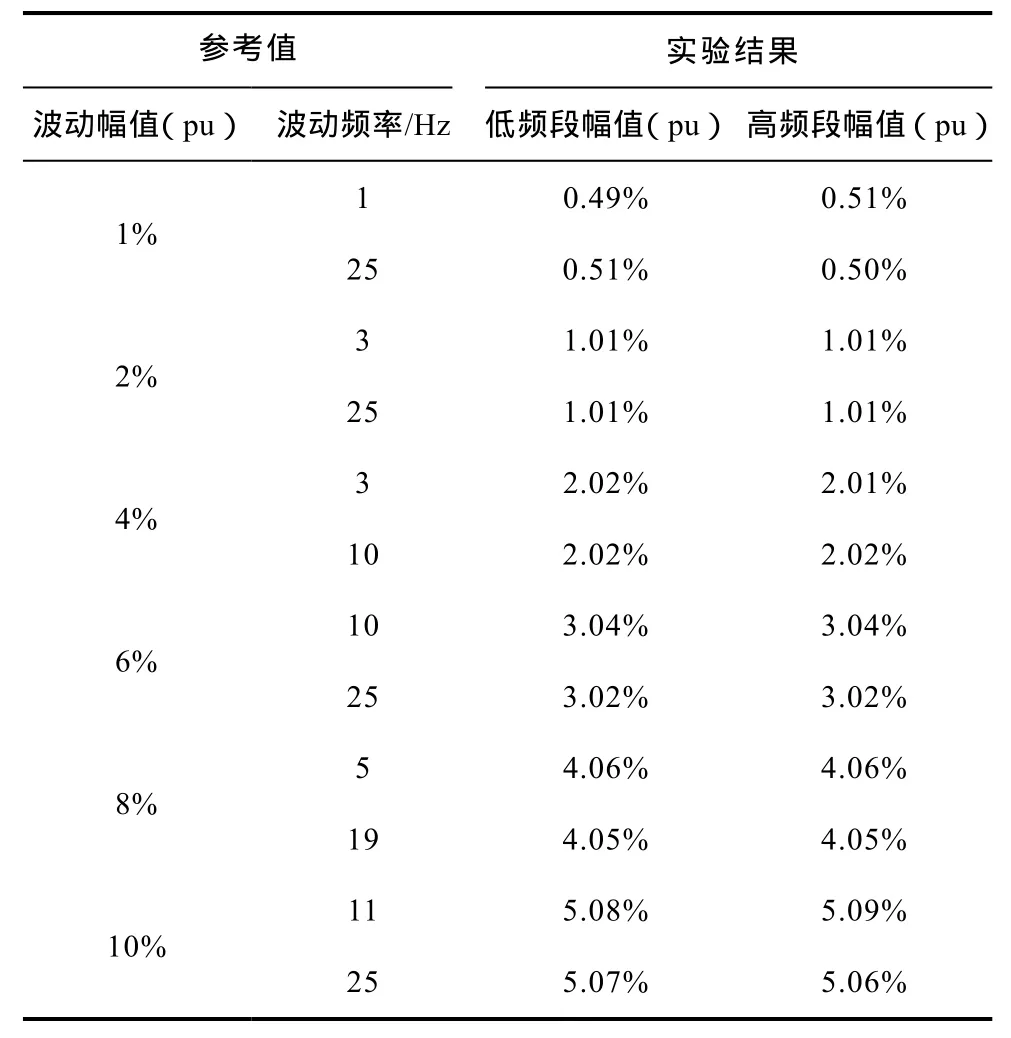
表3 不同波动频率和幅值的高低频段分量幅值Tab.3 Lower-sideband and upper-sideband amplitude components of divergent fluctuating frequency and amplitude

需要指出的是，在输出电压频率偏差以及模拟非对称电网故障时，由于不需要输出波动电压，图6中的指令信号并不是波动信号，而是具有特定幅值频率的正弦信号。根据现场的实验数据可以看出，使用 FRFC，测试装置可以根据需求调节输出电压的频率和幅值，保证波动电压精度和电压不平衡度精度，同时输出正常电压时THD小于2%。

4 结论

本文提出了一种用于分布式发电并网变流器测试的波动电压发生装置设计方案。测试装置电压等级可拓展，可匹配不同电压等级的分布式发电系统，同时在本文所提出的控制方案下，装置达到了以下性能指标：输出频率为 45～66Hz的额定电压，精度达到 0.01Hz，输出幅值为 20%～120%额定幅值的电压，误差小于0.1%；输出频率为0.5～25Hz和波动幅值为 0～10%基波电压幅值的波动电压，并且误差小于0.1%；输出不平衡度范围为 0～10%的三相不平衡电压，精度达到0.1%，并且输出三相不平衡电压时，负序电压幅值相位可调；输出额定电压的THD可以达到2%以下。

该方案有望为分布式发电并网变流器测试装置的设计提供一个可参考的标准。最后，本文以在基于所提出拓扑的“35kV-6MW风机变流器低频扰动测试装置”上进行的现场实验为例，充分证明了这种波动电压发生装置用于分布式发电并网变流器适应能力测试的可行性和有效性。

[1] GB/T 19963-2011,风电场接入电力系统技术规定[S].

[2] GB/T 19964-2012,光伏发电站接入电力系统技术规定[S].

[3] Peng F Z,Lai J S. A multilevel voltage-source inverter with separate DC sources for static var generation[J].IEEE Transactions on Industrial Applications,1996,32(5): 1130-1138.

[4] 孙运全,夷强,盛吉. 载波带频率变化的 PWM（VFCB-PWM）在级联有源电力滤波器中的应用[J].电力系统保护与控制,2010,38(10): 39-42.

Sun Yunquan,Yi Qiang,Sheng Ji. Variable-frequency carrier bands PWM(VFCB-PWM)and its applications in shunt APF[J]. Power System Protection and Control,2010,38(10): 39-42.

[5] 常伟,史丽萍,王思捷. 空间矢量调制技术在 6MW级静止同步补偿器中的应用[J]. 电力系统保护与控制,2012,40(12): 95-99.

Chang Wei,Shi Liping,Wang Sijie. Application of space vector modulation in 6kV cascade STATCOM[J]. Power System Protection and Control,2012,40(12): 95-99.

[6] 朱克平,江道灼. 一种改进型的光伏并网逆变器[J].电力系统保护与控制,2013,41(6): 99-104.

Zhu Keping,Jiang Daozhuo. An improved inverter for a grid-connected photovoltaic power system[J]. Power System Protection and Control,2013,41(6): 99-104.

[7] 高志刚,冬雷,李永东. 基于高频变压器的背靠背级联H桥型变换器[J]. 电工技术学报,2013,28(6):133-138.

Gao Zhigang,Dong Lei,Li Yongdong. Research on back to back cascaded H-bridge converter based on high frequency transformer[J]. Transactions of China Electrotechnical Society,2013,28(6): 133-138.

[8] 袁志昌,宋强,刘文华. 规则采样对载波移相SPWM 输出基波相位滞后的影响[J]. 电工技术学报,2010,25(11): 107-112.

Yuan Zhichang,Song Qiang,Liu Wenhua. The effect of regulated sampling on phase delay of phase-shift SPWM output[J]. Transactions of China Electrotechnical Society,2010,25(11): 107-112.

[9] 宫力,康勇,陈晶晶. 链式 STATCOM 直流电容电压分布式控制[J]. 电工技术学报,2011,26(10): 217-223.

Gong Li,Kang Yong,Chen Jingjing. DC capacitor voltage distributed control system for cascaded multilevel STATCOM[J]. Transactions of China Electrotechnical Society,2011,26(10): 217-223.

[10] Song Q,Liu W H. Control of a cascade STATCOM with star configuration under unbalanced conditions[J]. IEEE Transactions on Power Electronics,2009,24(1): 45-58.

[11] IEC 61000-4-27,Electromagnetic Compatibility(EMC),Testing and measurement techniques-Unbalance,immunity test for equipment with input current not exceeding 16 A per phase-Part 4-27.

[12] GB/T 15543-2008,电能质量 三相电压不平衡[S].

[13] IEC 61000-4-15,Electromagnetic Compatibility(EMC),Testing and measurement techniques,Flickermeterfunction and design specifications-part 4-15.

[14] Yong J,Tayjasanant T,Wilsun X,et al. Characterizing voltage fluctuations caused by a pair of interharmonics[J]. IEEE Transactions on Power Delivery,2008,23(1): 319-327.

[15] Li Y F,Wang Y,Feng Y P,et al. Research on control method for avoiding transformer magnetic biasing in cascaded H-bridge multilevel inverters[C]. Proceedings of IEEE International Power Electronics and Motion Control Conference,2012: 1965-1970.

[16] Dong D,Thacker T,Burgos R,et al. On zero steadystate error voltage control of single-phase PWM inverters with different load types[J]. IEEE Transactions on Power Elecronics,2011,26(11): 3285-3297.