基于自适应模糊滑模的复合控制导弹制导控制一体化反演设计

王昭磊，王青，冉茂鹏，董朝阳

（1.北京航空航天大学自动化科学与电气工程学院，北京100191；2.北京航空航天大学航空科学与工程学院，北京100191）

基于自适应模糊滑模的复合控制导弹制导控制一体化反演设计

王昭磊1，王青1，冉茂鹏1，董朝阳2

（1.北京航空航天大学自动化科学与电气工程学院，北京100191；2.北京航空航天大学航空科学与工程学院，北京100191）

针对姿控式直接力/气动力复合控制导弹，提出一种基于滑模反演控制的制导控制一体化控制律。通过引入指令滤波器，避免了传统反演设计存在的计算膨胀问题；设计自适应模糊逼近器对系统不确定函数进行逼近，并构造误差滑模面来补偿模糊逼近误差及有界干扰对系统的影响，通过在线自适应调整控制律参数实现系统的鲁棒性。具体的数值算例仿真计算表明：在目标机动的情况下，所设计的一体化制导控制系统具有较强的抗干扰能力，在保证系统稳定的同时可达到满意的制导控制效果。

控制科学与技术；复合控制；制导控制一体化；反演控制；滑模控制；自适应模糊控制

0　引言

传统制导与控制方法将制导回路与控制回路分开设计，导致制导系统与控制系统之间缺乏协调匹配，无法充分发挥导弹的最大潜力。制导控制一体化设计将制导回路同控制回路作为整体来研究，可有效地解决指令跟踪性能、操纵性能与稳定性能之间的矛盾，提升飞行器作战响应速度及攻击精度，以适应复杂战场环境。因此，制导控制一体化研究成为近年来研究热点之一［1-2］。

针对编队飞行问题，Kim等［3］基于自适应输出反馈和反演控制技术设计了制导控制一体化系统，采用神经网络在线补偿系统未建模非线性项。Koren等［4］针对敏捷性导弹制导控制一体化问题，采用常规滑模方法设计控制律，实现了对非线性开关型舵机建模误差及目标机动的鲁棒性。董飞垚等［5］将一体化设计问题转化为3阶积分链系统镇定问题，结合鲁棒高阶滑模和超扭曲算法设计了控制律，但系统不确定性实际仅由目标机动引起。宋海涛等［6］采用自适应动态面方法设计了一体化控制律，但仅考虑了建模误差的影响。

另一方面，随着空中威胁的日益增强，新一代防空导弹的机动性和快速响应能力成为其重要的性能指标。空气舵作为单一执行机构很难满足制导精度要求，而直接力控制技术可有效提高弹体机动性和响应速度，因此采用直接力/气动力复合控制技术成为提高制导精度的必要手段。但直接力的开启使得飞行中气动参数有较大摄动，并引起复杂的非线性及耦合现象，使得复合控制导弹的制导控制一体化设计面临更大挑战［7］。

Shtessel等［8］基于高阶滑模理论，设计了直接力/气动力复合控制导弹的制导控制一体化系统，保证了对目标机动和模型不确定性的鲁棒性，但设计过程复杂、计算量大。舒燕军等［9］针对轨控式复合控制导弹的制导控制一体化问题，基于反演设计和非线性干扰观测器技术设计了控制律，但并未考虑直接力建模，控制量仅为舵偏量。

本文针对姿控式直接力/气动力复合控制导弹，基于反演控制方法设计了一体化制导控制律，并引入指令滤波器，避免了传统反演设计存在的计算膨胀问题；同时考虑目标机动、建模误差和气动参数摄动等不确定性影响，并将其视为复合干扰，设计了自适应模糊逼近器对系统不确定函数进行逼近，并利用自适应滑模方法补偿模糊逼近误差及有界干扰对系统影响，同时在线自适应调整控制律参数实现系统对复合干扰的鲁棒性，保证了一体化制导控制律具有良好效果。

1　问题描述

1.1弹目相对运动数学模型

本文研究导弹采用不旋转机制，由于俯仰和偏航通道有相似结构，根据导弹轴对称性以纵向平面内俯仰通道为例来说明直接力/气动力复合控制导弹的制导控制一体化设计过程，偏航通道的设计过程可用类似方法得到。

为研究导引规律，如图1所示，O0X0Y0为惯性系，原点O0为导弹发射点，M、T分别为导弹和目标。选取视线坐标系O1X1Y1作为末制导参考系，原点O1位于导弹质心，X1轴沿视线方向，指向目标为正，Y1位于纵向平面内与X1轴垂直，向上为正。

图1 弹目相对运动关系图Fig.1 Relative motion between missile and target

图1中：R为弹目相对距离；q为视线角；vM、vT分别为导弹和目标速度；θM、θT分别为导弹和目标的弹道倾角。

由于末制导段vM、vT可认为常值，则由图1可得弹目相对运动模型［10］为

式中：aM、aT分别为导弹与目标在Y1方向的加速度。

1.2直接力数学模型建立

姿控式复合控制导弹直接力由安装在弹体质心前的微型侧喷发动机喷出的燃气流产生的，侧喷发动机共有18个×10环，共180个，呈环状在弹体前端排列，奇偶数环相互交错10°布局，如图2所示，其中O2X2Y2为弹体系，且直接力Tc相对于O2Y2轴转动的角度记为ξ.

忽略奇偶环直接力作用点到导弹质心的距离差距，可认为每环沿弹体圆周相隔10°均匀分布的36个侧喷发动机［7］，且将同一角度ξ的侧喷发动机视为一列，则每列共5个侧喷发动机可供使用。

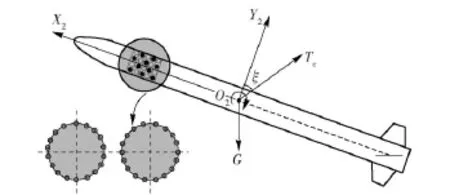
图2　姿控式复合控制导弹结构图Fig.2 Configuration of blended control missile with lateral jets

而已知单个微型侧喷发动机的推力T随时间的变化规律［11］为

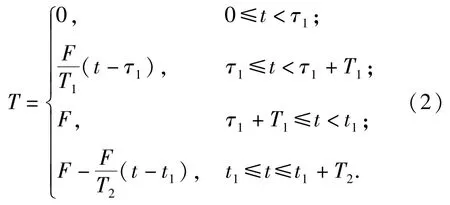
式中：F为姿控发动机稳态推力；τ1为推力延迟时间；T1为推力由0增至稳态值的时间；t1为发动机关机指令时刻；T2为推力由稳态值降至0的时间。则总的直接力Tc可表示为

式中：n为每列小火箭消耗的个数，1≤n≤5.

1.3纵向平面一体化模型建立

考虑到末制导阶段主发动机已关机，纵向平面内直接力/气动力复合控制导弹动态方程［11］为

式中：m为导弹质量；α为迎角；β为侧滑角；Q为动压；S为特征面积；L为特征长度；为气动导数；δz为升降舵偏角；LT为侧喷发动机到导弹质心的平均距离。

据几何关系知：

故由（6）式知，（7）式可改写为

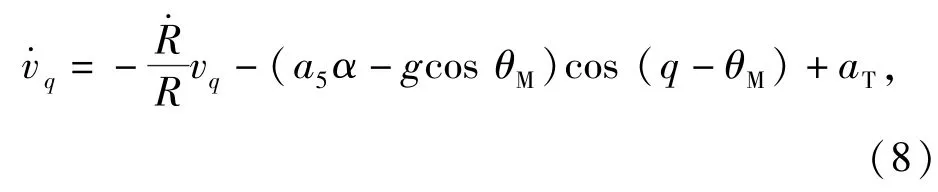
为便于设计，对一体化方程进行简化，假设β≈ 0，q-θM≈0［9］，且令则根据（4）式和（8）式可得制导控制一体化模型：

式中：dvq为目标机动aT引起的有界干扰［9］，而考虑通道解耦与模型简化过程中存在的建模误差［6］，可假设系统存在未知有界干扰［6，10］.

式中：

同时，由于存在气动参数摄动，f1（x1）、f2（x2）和f3（x2，x3）可能无法精确得到，可见系统（10）式为带有不确定性的严反馈非线性系统，将目标机动、建模误差和气动参数摄动定义为复合干扰，则本文设计目标为控制x1收敛至0，且保证系统对复合干扰具有良好的鲁棒性。

2　一体化制导控制律设计

下面以（10）式给出的一体化模型作为被控对象，利用反演法分3步进行制导控制一体化设计，同时采用自适应模糊逼近器对系统不确定函数进行逼近，并结合自适应滑模方法来补偿模糊逼近误差及有界干扰对系统的影响。

2.1制导控制一体化系统控制器设计

步骤1 对（10）式中子系统1进行外环设计。由于滑模控制关键是寻找合适的滑动模态超平面，考虑设计子系统1的滑模面如下形式：

当系统滑动到该超平面时，状态将以时间常数的指数下降，从而得到渐近稳定状态x1→0，从而实现平行接近导引律。将s1对时间t求导得

由于f1（x1）可能无法精确得到，选择由中心平均模糊消除器、乘积推理规则、单值模糊产生器构成的自适应模糊系统来逼近f1（x1）。假设存在最优逼近函数

然而一般情况下，无法得到最优参数θ*，只有它们的估计值记为

因此，利用模糊自适应逻辑系统对未知函数f1（x1）进行逼近可得

式中：ε1为外环逼近误差，满足，且有

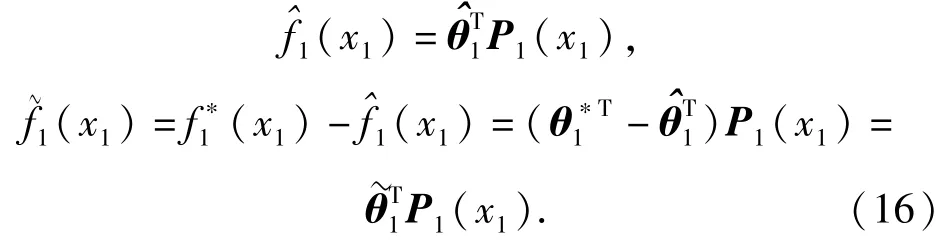
则（12）式可改为如下形式：

同时为消除目标机动引起的d1项及逼近误差ε1的影响，通过自适应滑模方法对其进行补偿。视x2为外环控制量，故虚拟控制量指令x2c可写为

控制律中x2c1=-k1s1为负反馈部分，实现了状态反馈，为模糊自适应部分，其中滑模项用来补偿模糊逼近误差。为自适应滑模补偿部分，用来补偿干扰项d1的影响。且由于系统的不确定参数均未知，给出如下在线自适应律：

步骤2 对（10）式中子系统2进行中环设计，以实现攻角虚拟控制量跟踪，即，其中，由外环子系统的虚拟控制量（20）式提供，则可设计子系统2的滑模面如下形式：

将s2对时间t求导可得

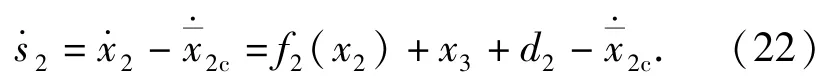
用类似于步骤1方法对未知函数f2（x2）逼近可得

式中：ε2为中环逼近误差，满足，且有

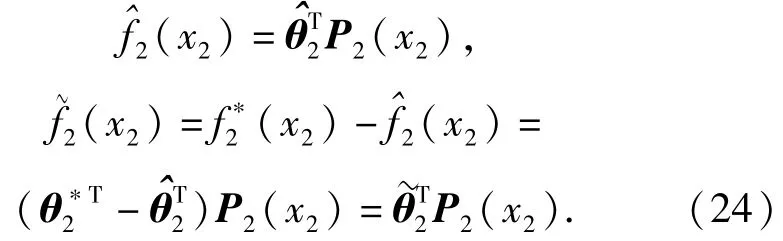
故（22）式可改为如下形式：

视x3为中环控制量，故虚拟控制量指令x3c可写为

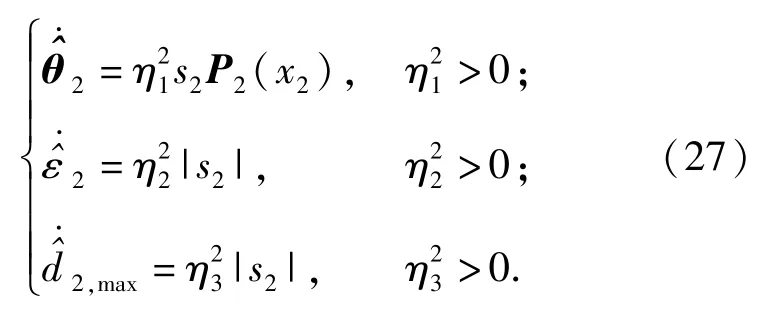
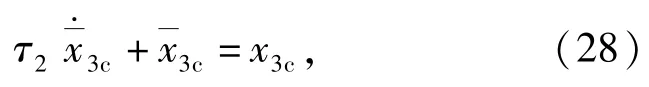
步骤3 对（10）式中子系统3进行内环设计。求得控制量u，以实现俯仰角速率虚拟控制量的跟踪，即，第3个子滑模面设计如下：

将s3对时间t求导可得

同理，可对未知函数f3（x2，x3）进行逼近得

式中：ε3为内环逼近误差，满足，且有

故（30）式可改为如下形式：

故控制量u可写为

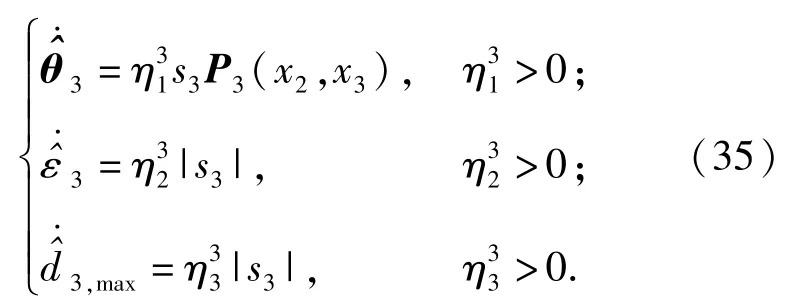
综上所述，给出完整的一体化控制律如下：

2.2稳定性分析

同理，将（26）式和（29）式代入，可将（25）式重写为

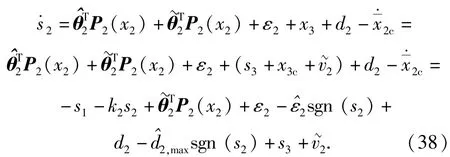
将（34）式代入，可将（33）式重写为

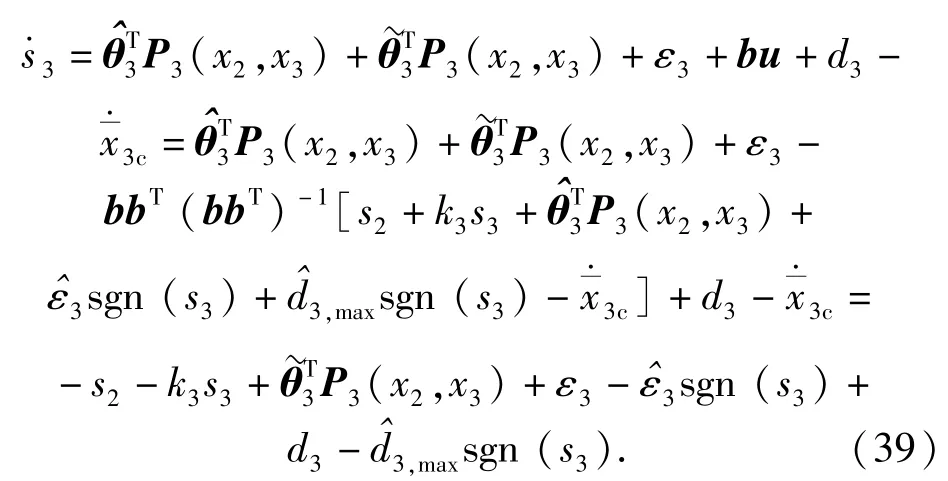
定理 对存在有界不确定干扰的制导一体化系统（10）式，采用自适应滑模方法处理有界不确定干扰，且采用模糊自适应系统对不确定函数f1（x1）、f2（x2）和f3（x2，x3）进行逼近。取模糊自适应滑模控制律（36）式，及自适应调参律（19）式、（27）式和（35）式，则能保证整个闭环系统一致最终有界，系统跟踪误差收敛到原点附近任意小的紧集，即保证对复合干扰具有良好鲁棒性的同时使得x1趋于0.

证明 取如下的准Lyapunov函数：

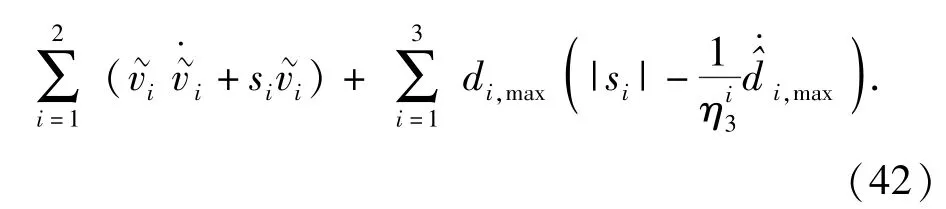
由自适应参数调节律（19）式、（27）式和（35）式可得

故将（44）式代入（43）式，可得

由于必存在正数κi，使得，故应用Young不等式ab＜a2/2+b2/2，可得

则（45）式可改写为

将（47）式整理为

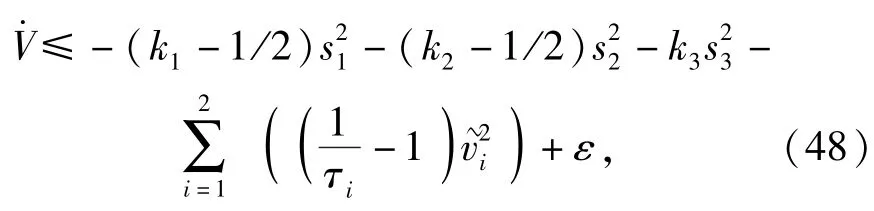
显然，整个误差空间为不变集，根据LaSalle's定理［12］，闭环系统一致最终有界，系统跟踪误差收敛原点附近任意小的紧集。故（36）式的一体化制导控制律可保证在末制导过程中x1→0，证毕。

3　仿真分析

导弹初始位置（xM，yM）为（0 m，11 000 m），初始速度Ma数为5.5，目标初始位置（xT，yT）为（15 000 m，26 000 m），初始速度Ma数为5.导弹俯仰通道各标称气动力参数如表1所述。

其他仿真参数如下：k1=28，k2=1.7，k3=1.7，，，假设，取模糊基函数为

表1　特征点的标称气动参数Tab.1 Nominal aerodynamic parameters of feature points

目标初始弹道倾角θT0为200°，导弹初始弹道倾角θM0为30°.对所提出的自适应模糊滑模控制律在纵向平面中对高速俯冲目标的拦截效果进行研究。仿真过程中分别考虑标称模型及含有复合干扰项情况，其中标称模型时目标无机动，不存在气动参数摄动且扰动信号d2=d3=0；而复合干扰项包括目标以7 g过载、频率蛇形机动，所有气动参数进行±20%的随机拉偏（频率为2 Hz，幅值为±20%的方波信号），d2=0.2sin（πt/2）和d3= 0.1sin（πt/2）.结果对比如图3～图11所示：图3为弹目相对运动曲线，标称模型下脱靶量为0.640 2 m，带有复合干扰项脱靶量为0.937 8 m；图4为垂直于视线方向的弹目相对速度vq，可看出vq趋近于0，达到了控制律设计目的；图5为攻角响应曲线；图6为俯仰角速率ωz响应曲线；图7为升降舵偏角δz响应曲线，可看出舵δz在±30°以内；图8为直接力响应曲线，可看出在跟踪误差较大时，直接力动作较大；图9～图11为设计的滑模面响应曲线，均收敛到0，满足控制要求。

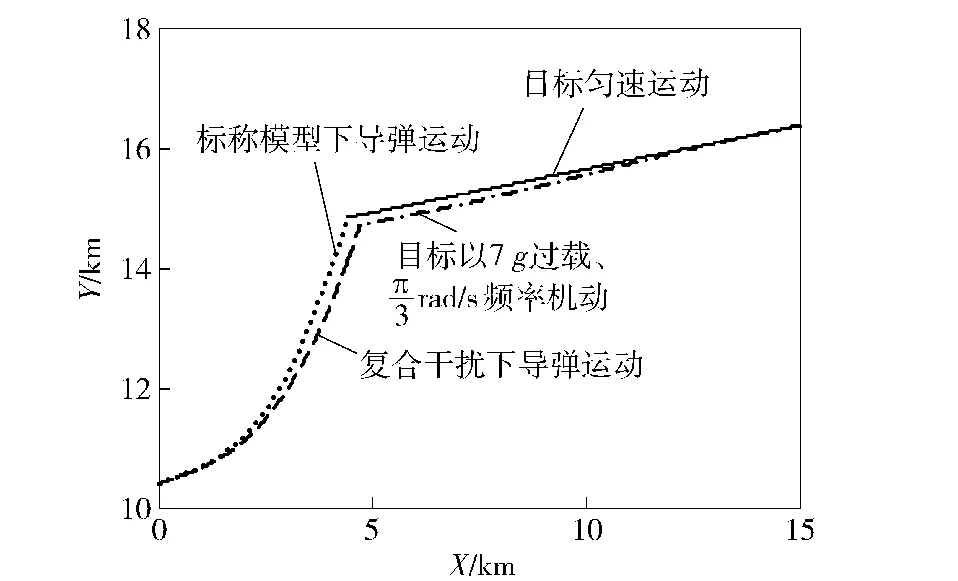
图3　弹目相对运动轨迹图Fig.3 Missile-target interception trajectories

图4　垂直于视线方向的弹目相对速度vqFig.4 Curve of vqvertical to the line-of-sight direction

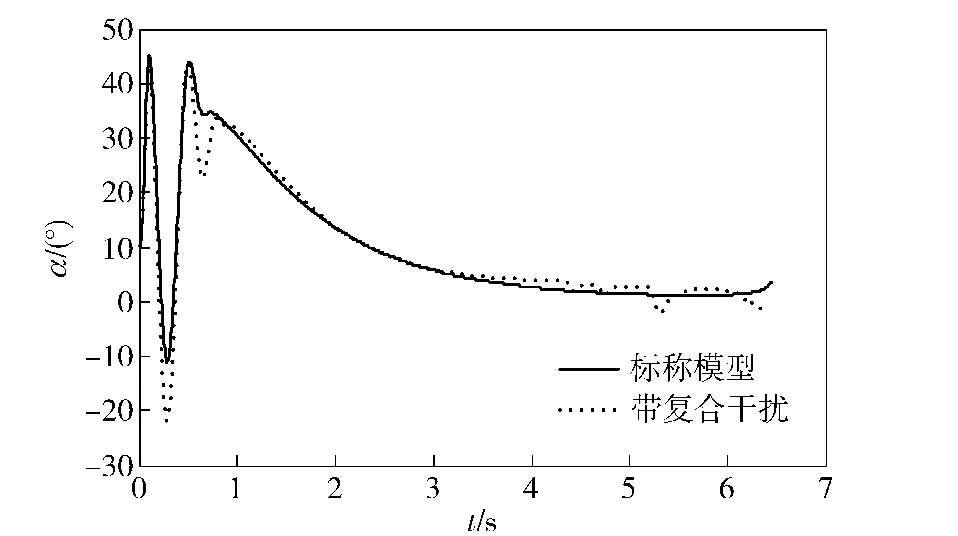
图5　攻角α曲线Fig.5 Curve of attack angle α

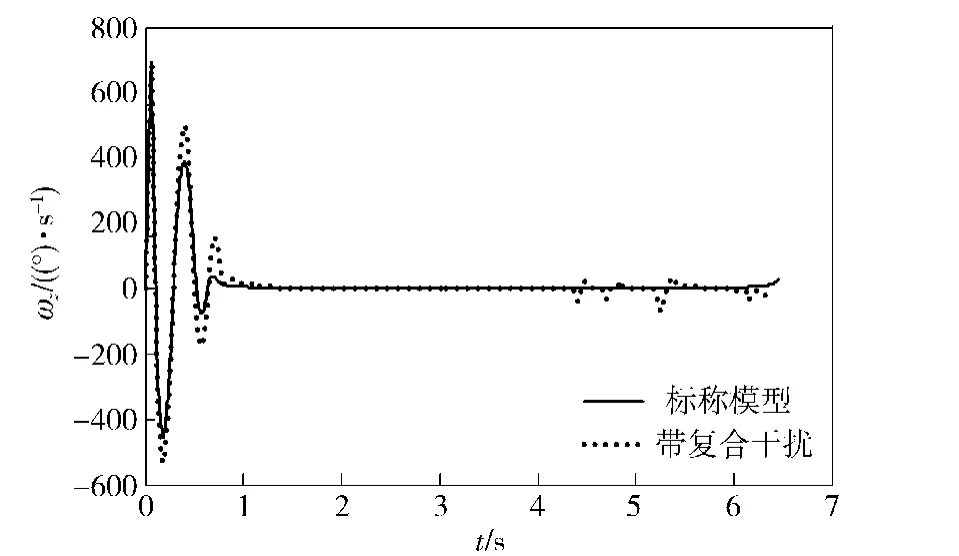
图6　俯仰角速率ωz响应曲线Fig.6 Curve of pitch rate ωz

图7　升降舵偏角δz的响应曲线Fig.7 Curve of control deflection δz

图8　直接力使用情况Fig.8 Curve of lateral jet

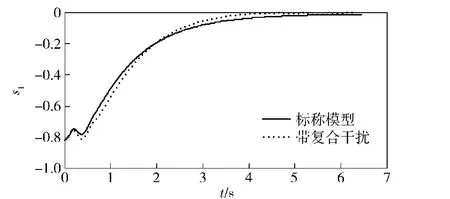
图9　滑模面s1的响应曲线Fig.9 Curve of surface s1

图10　滑模面s2的响应曲线Fig.10 Curve of surface s2

图11　滑模面s3的响应曲线Fig.11 Curve of surface s3

4　结论

本文针对姿控式直接力/气动力复合控制导弹，利用反演法分3步进行了制导控制一体化设计，并引入指令滤波方法避免了“计算膨胀”问题，同时利用模糊自适应系统对系统不确定函数进行逼近，并构造自适应误差滑模面来补偿逼近误差及有界干扰的影响，提高了系统鲁棒性。仿真结果表明：在高马赫数末制导拦截问题上，所设计的一体化制导控制律具备满意的鲁棒性能，能够抑制目标机动、建模误差和气动参数摄动等不确定性影响，制导精度较高，控制性能良好。

（

）

［1］Maital L，Tal S，Shual G.Linear quadratic integrated vs separated autopilot-guidance design［J］.Journal of Guidance，Control，and Dynamics，2013，36（6）：1722-1730.

［2］薛文超，黄朝东，黄一.飞行制导控制一体化设计方法综述［J］.控制理论与应用，2013，30（12）：1511-1520. XUE Wen-chao，HUANG Chao-dong，HUANG Yi.Design methods for the integrated guidance and control system［J］.Control Theory&Applications，2013，30（12）：1511-1520.（in Chinese）

［3］Kim B S，Calise A J，Sattigeri R J.Adaptive，integrated guidance and control design for line-of-sight-based formation flight［J］.Journal of Guidance，Control，and Dynamics，2007，30（5）：1386-1398.

［4］Koren A，Idan M，Golan O M.Integrated sliding mode guidance and control for a missile with on-off actuators［J］.Journal of Guidance，Control，and Dynamics，2008，31（1）：204-214.

［5］董飞垚，雷虎民，周池军，等.导弹鲁棒高阶滑模制导控制一体化方法研究［J］.航空学报，2013，34（2）：1-7. DONG Fei-yao，LEI Hu-min，ZHOU Chi-jun，et al.Integrated robust high order sliding mode guidance and control for missiles［J］.Acta Aeronautica et Astronautica Sinica，2013，34（2）：1-7.（in Chinese）

［6］宋海涛，张涛，张国良，等.考虑建模误差的拦截弹制导控制一体化设计［J］.兵工学报，2013，34（9）：1167-1172. SONG Hai-tao，ZHANG Tao，ZHANG Guo-liang，et al.Integrated design of interceptor guidance and control considering modeling error［J］.Acta Armamentarii，2013，34（9）：1167-1172.（in Chinese）

［7］姚郁，毕永涛.姿控式直接侧向力与气动力复合控制策略设计［J］.航空学报，2010，31（4）：701-708. YAO Yu，BI Yong-tao.Design of blended control strategy for missiles with lateral jets and aerodynamic surfaces［J］.Acta Aeronautica et Astronautica Sinica，2010，31（4）：701-708.（in Chinese）

［8］Shtessel Y B，Tournes C H.Integrated higher-order sliding mode guidance and autopilot for dual-control missiles［J］.Journal of Guidance，Control and Dynamics，2009，32（1）：79-94.

［9］舒燕军，唐硕.轨控式复合控制导弹制导与控制一体化反演设计［J］.宇航学报，2013，34（1）：79-85. SHU Yan-jun，TANG Shuo.Integrated guidance and control backstepping design for blended control missile based on NDO［J］. Journal of Astronautics，2013，34（1）：79-85.（in Chinese）

［10］Han Y，Ji H.Integrated guidance and control for dual-control missiles based on small-gain theorem［J］.Automatica，2012，48：2686-2692.

［11］马克茂，赵辉，张德成.导弹直接侧向力与气动力复合控制设计与实现［J］.宇航学报，2011，32（2）：310-316. MA Ke-mao，ZHAO Hui，ZHANG De-cheng.Control design and implementation for missiles with blended lateral jets and aerodynamic control systems［J］.Journal of Astronautics，2011，32（2）：310-316.（in Chinese）

［12］Khalil H K.Nonlinear system［M］.3rd ed.Beijing：Publishing House of Electronics Industry，2011.

Integrated Guidance and Control Backstepping Design of Blended Control Missile Based on Adaptive Fuzzy Sliding Mode Control

WANG Zhao-lei1，WANG Qing1，RAN Mao-peng1，DONG Chao-yang2
（1.School of Automation Science and Electrical Engineering，Beihang University，Beijing 100191，China；2.School of Aeronautic Science and Engineering，Beihang University，Beijing 100191，China）

An integrated guidance and control law is proposed for dual-control missiles based on the backstepping sliding mode design approach.A command filter is introduced to eliminate the computation explosion problem of conventional backstepping design method.An adaptive fuzzy approximator is employed to approximate the system uncertain functions，and a sliding mode surface is constructed to compensate the effects of approximate error and bounded disturbances.The controller parameters are adjusted adaptively on-line to guarantee the robustness of the system.A numerical example is provided.The simulation results show that the integrated guidance and control approach has robustness to disturbances and improves the control performance while ensuring the operating stability of system when a target maneuvers with high acceleration.

control science and technology；dual control；integrated guidance and control；backstepping；sliding-mode control；adaptive fuzzy control

V448.12

A

1000-1093（2015）01-0078-09

10.3969/j.issn.1000-1093.2015.01.012

2014-02-12

国防预先研究基金项目（9140C48020212HK0101）

王昭磊（1986—），男，博士研究生。E-mail：beiliwzl123@163.com；王青（1968—），女，教授，博士生导师。E-mail：wangqing@buaa.edu.cn