信号交叉口车辆到达规律分析

蒋阳升　韩世凡　吴　婷　张　改

1. 交通运输智能化国家地方联合工程实验室，成都 610031

2. 综合运输四川省重点实验室，成都 610031

3. 西南交通大学，交通运输与物流学院，成都 610031

4. 江苏智通交通科技有限公司，南京 210000

信号交叉口车辆到达规律分析

蒋阳升1,2,3韩世凡1,2,3吴婷1,2,3张改4

1. 交通运输智能化国家地方联合工程实验室，成都 610031

2. 综合运输四川省重点实验室，成都 610031

3. 西南交通大学，交通运输与物流学院，成都 610031

4. 江苏智通交通科技有限公司，南京 210000

信号交叉口是中断车流的重要结点，其车流到达规律的准确描述是交叉口信号控制设计的重要影响因素。信号交叉口车流的到达规律是随机且多样的，并服从一定的统计规律。本文对信号交叉口到达车流的到达时间间隔的统计分析进行拟合，发现信号交叉口车流的到达规律与其变异系数的平方存在耦合关联，并得出结论如下：对数正态分布的拟合范围为0.8874～0.9904，平均拟合度高达0.9489，拟合效果最佳；伽马分布的拟合度范围为0.5352～0.9449，平均的拟合度为0.8056，拟合效果次之；威布尔分布拟合度在0.1997～0.8991之间，总体波动较大，平均的拟合度为0.616；正态分布拟合范围为0.2585～0.6671，平均拟合度为0.6252；指数分布拟合度范围是0.0365～0.4077，平均拟合度是0.2317，拟合效果最差。

信号交叉口；车流到达规律；变异系数；车头时距

0 引 言

城市信号交叉口，作为中断车流的重要结点，其车流到达规律的准确描述直接影响到信号交叉口车辆排队延误[1]模型的建立，和微观仿真模型的适用性及其结果的准确性，是交叉口信号控制设计的重要影响因素。

信号交叉口车流的到达规律是随机且多样的，并在不同的车流条件下服从不同的统计规律[2-3]，如交通流密度较小时服从正态分布，较大时服从指数分布等。由于车流的车头时距是描述车辆到达信号交叉口规律的关键，因此，对信号交叉口的车流到达规律的分析等同于对信号交叉口到达车流的车头时距规律的分析。当前对于车流车头时距[4-8]的研究主要是从定性的角度来获得车头时距与交通流状态[9]之间的关系，得到的车辆到达规律相对单一，且缺乏定量的标准来确定车流到达规律，无法准确的描述信号交叉口的车辆到达规律。鉴于此，本文选择某信号交叉口进行调查，以信号交叉口某一方向的停车线为对象，获得车流到达时间间隔数据，采用多种不同的统计规律对车流的到达时间间隔进行拟合，由于变异系数[10]是衡量各观测数据变异程度的统计量，即变异系数代表了该数据的灵敏度，因此，本文以变异系数作为判断车流到达规律的定量基础，最终得出信号交叉口车流的到达规律与变异系数之间的耦合关系。

1 信号交叉口车流到达数据获取

1.1调查地点选取

信号交叉口车辆到达规律会受到诸多因素的影响[8]，包括车道几何因素、信号控制方案、道路交通组织方案等。为尽量减少客观因素对信号交叉口车流到达规律的影响，需选择无单行及特殊时段限行、交叉口排队长度不过长、车道组受周围非机动、行人干扰较小以及交叉口具有较强的高峰—平峰特性的交叉口作为调查对象。

基于以上几点要求，为使数据能充分反应信号交叉口车流到达的实际情况，经过预调查后，确定以成都市区一环内位于西大街、八宝街、宁夏街、长顺下街四条道路相交形成的十字信号交叉口作为调查地点，并对西大街进行调查，如图1所示：

图1　信号交叉口示意Fig.1 The signalized intersection

1.2调查时间选取

虽然到达交叉口的交通流及其到达规律随调查日期、调查时间段的选取不同而不同，但本文研究的是一般的、任意的车流到达规律，所以，时间特性对于本研究的影响很小，故选取2012年11月29日星期四作为调查时间，进行现场数据的调查与视频拍摄，每次调查时间为60 min。

1.3调查数据提取

通过在Excel中编写程序，可实现点击操作控件按钮来记录当前时刻，进而提取车辆到达的时间间隔。具体操作为：使用视频播放器播放视频资料，当车辆的车头经过预设位置时，点击空间按钮，即可记录车辆的到达时刻，通过前后车辆到达时刻之差可获得车辆的到达时间间隔。需注意的是，记录数据时不用区分道路车道，获取的车辆时间间隔包括该路段所有车道的车辆，而非单一的车道。目标是获得整个路段所有车辆到达交叉口的时间间隔，进而分析得出车辆到达交叉口的到达规律，因此，本文的研究更加符合实际情况。

因本文研究对象是车辆的到达时间间隔，故将每个周期所调查获得的车辆到达时间间隔作为一组数据。经实地调查，共获得33组数据备用。

2 信号交叉口到达车流统计与拟合

2.1数据随机性检验

为保证数据的合理性，需在进行统计分析拟合之前对数据进行随机性检验。利用SPSS软件对车辆到达时间间隔数据进行游程检验，取置信区间为95％，得到如表1所示的统计显著性。

表1　车辆到达时间间隔游程检验的统计显著性Tab.1 The statistical significance of running test for vehicle arrival time

从表1可以看出，33组数据的显著性均大于显著性水平0.05，说明调查数据均为随机序列，可进行统计分布的拟合。

2.2常用分布的筛选

常用的分布，除了引言当中提到的正态分布和指数分布，本文还选择了伽马分布、威布尔分布、对数正态分布、负指数分布、Logistic分布、Pareto分布等8种常用的双参数理论分布来进行初期数据拟合，并筛选出对调查数据拟合效果相对较好的5种分布来进行数据拟合比较。这5种概率分布分别为：伽马分布（R1）、威布尔分布（R2）、对数正态分布（R3）、正态分布（R4）以及指数分布（R5）。

2.3数据分布拟合比较

根据前述分析，首先对在信号交叉口获得的33组数据分别进行变异系数的计算，所得各周期变异系数可参见表2。根据MATLAB软件编程实现对数据在各种分布情况下的可决系数的计算，按照变异系数从低到高的顺序排列得到表3，并获得车辆到达信号交叉口时间间隔的数据分布拟合对比图，本文随机选择15个周期的数据分布拟合对比得到图2。

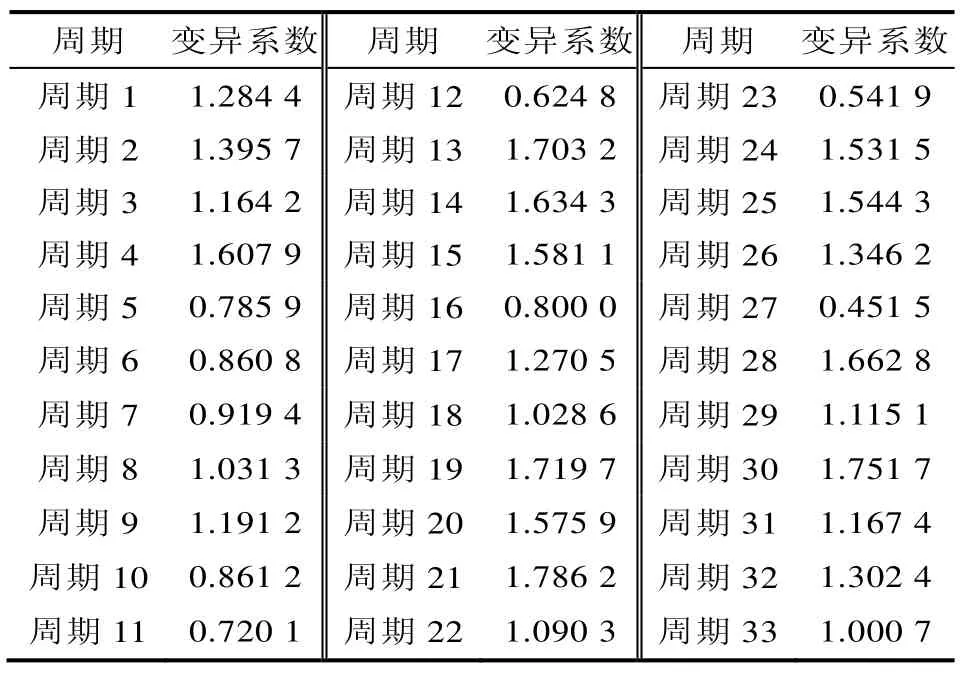
表2　西大街各周期变异系数Tab.2 The coefficients of variation for each cycle of the West Street

表3　西大街各分布的可决系数值Tab.3 The distribution determination coefficients of the West Street

续表3　

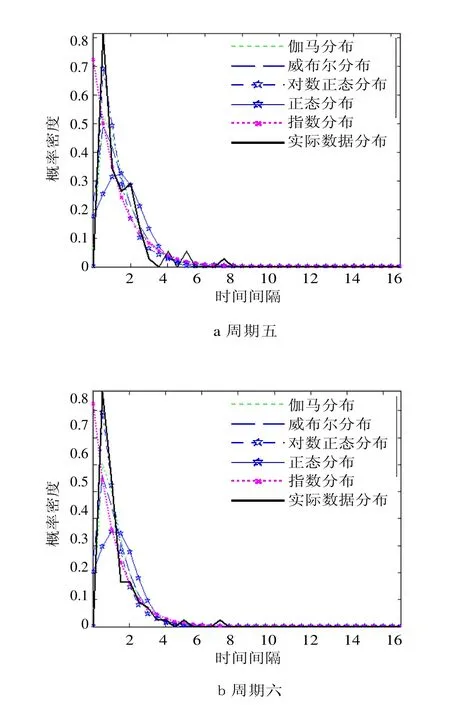
图2　车辆到达信号交叉口时间间隔的数据分布拟合对比Fig.2 Fitting comparison of vehicle arrival time data distributions at the signalized intersection

从表3和图2可以大致看出，在各种分布中对车辆到达信号交叉口时间间隔数据的拟合效果最好的是对数正态分布，表明对数正态分布可以很好地拟合车辆在不同时段到达信号交叉口的到达规律。但为了能更好地比较各种分布在不同变异系数（C2）下的拟合效果，可根据表3数据绘制图3。

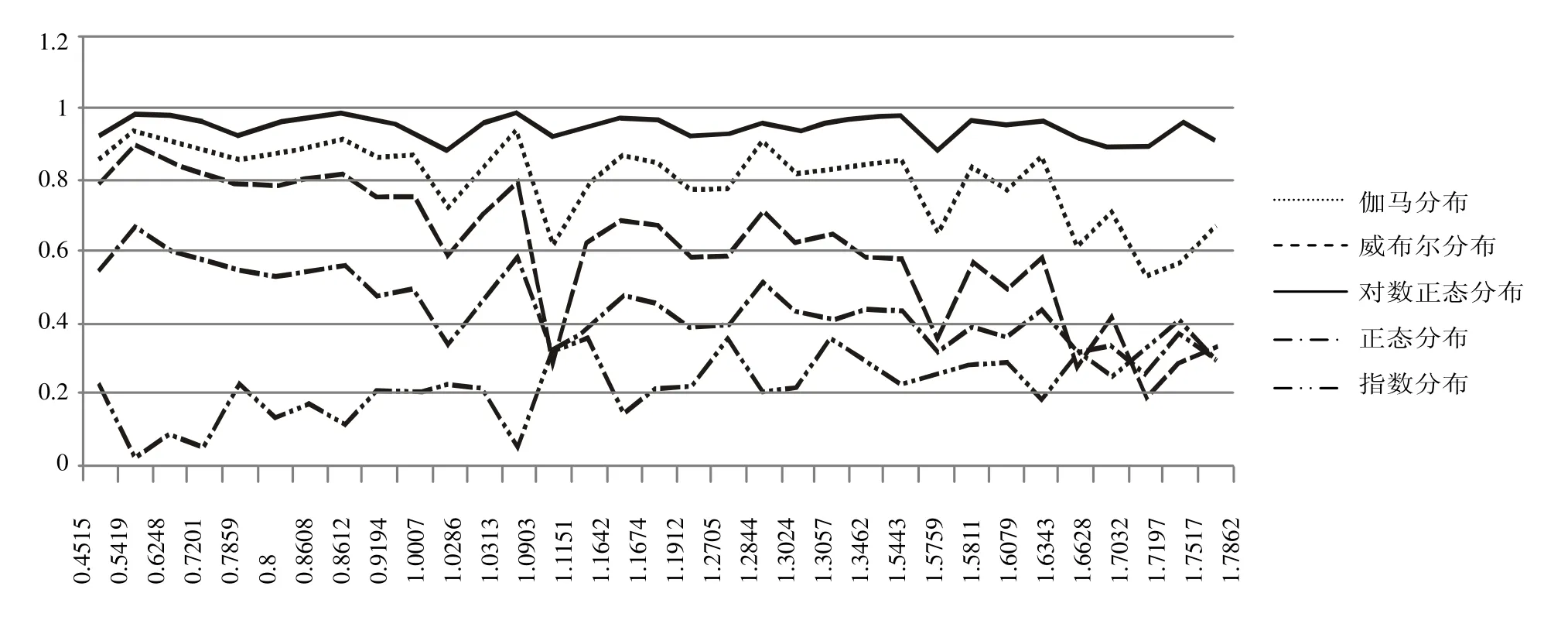
图3　各拟合分布的可决系数分布Fig 3 Determination coefficients of each fitted distribution

2.4结果分析

通过上一节分析，并根据各分布拟合下所得出的可决系数和个周期实际计算的变异系数可以得出以下结论：

（1）对数正态分布的拟合效果很稳定，可决系数即拟合效果主要是在0.8874～0.9904之间，平均拟合度为0.9489，拟合度很高，且始终排在第一位。那么，在进行城市信号交叉口车流微观仿真时，对数正态分布是最贴近实际且适合的选择。但是，因为该分布不具有Markov性质，因此，一般不用于排队建模分析，这也与目前众多论文中很少见到以对数正态分布拟合车流到达规律的情况相符合。

（2）伽马分布的拟合效果也较好，可决系数在0.5352～0.9449之间时，平均的拟合度为0.8056。变异系数平方在0.45～1.0之间时，伽马分布的拟合效果很稳定，在变异系数平方为1.0的右端，该分布的拟合效果和稳定性均相对于左端略差，有拟合效果逐渐变弱的趋势。与拟合效果最好的对数正态分布相比，伽马分布的拟合度要低0.1433，排在第二位。因此，对城市信号交叉口车流进行微观仿真时，伽马分布描述车流到达规律的第二选择。但因伽马分布也不具备Markov性质，因此，一般也不用该分布来进行排队建模分析。

（3）根据数据可看出，当变异系数平方为0.45～1.0之间时，威布尔分布的拟合效果较为稳定且拟合度较高，而在变异系数平方大于1.0时，该分布的拟合效果逐渐下降且不稳定。总体来看，威布尔分布的拟合效果良好，可决系数在0.1997～0.8991之间，平均的拟合度为0.616。因此，威布尔分布可以用于城市信号交叉口车流进行微观仿真，但不适用于进行交叉口的排队建模分析。

（4）正态分布的拟合效果总体趋于稳定，但是，拟合度都相对较低，可决系数在在0.2585～0.6671之间。当变异系数平方小于0.8612时，拟合效果一般，平均拟合度为0.6252；当变异系数平方大于0.8612时，拟合效果较差，平均拟合度为0.4。由此可见，在进行微观仿真时，正态分布并不适用。但是，因正态分布具有Markov性质，虽然其拟合效果不是很高，但仍时常应用在排队建模分析之中。

（5）从图2可以看出，指数分布的拟合效果随着变异系数平方的增加而呈现上升的趋势。但整体的拟合度都比较低，并不适用于交叉口车辆到达的微观仿真。同样的，因为指数分布具有Markov性质，且经过恰当的变形，如特殊的指数分布——负指数分布常会用到排队建模分析当中。

3 结束语

本文选择成都市八宝街-宁夏街这一典型信号交叉口作为研究对象，选择常用以描述车头时距的伽马分布、威布尔分布、对数正态分布、正态分布、指数分布五种分布方式拟合车辆到达信号交叉口的车头时距，通过实例分析对比得到对数正态分布拟合效果最佳这一结论，为车辆到达典型信号交叉口的车头时距分布提出了科学合理的分布方式选择依据，但该结论对于其它类型的交叉口的适用性还需进一步研究以作验证。

[1] 陈绍宽，郭谨一，王 璇 等. 信号交叉口延误计算方法的比较[J]. 北京交通大学学报，2005，29（3）：77-80.

[2] 王 祺，李 力，胡坚明，邹 斌. 不同车头时距下交通流的速度分布[J]. 清华大学学报(自然科学版)，2011，51（3）：309-311.

[3] Catbagan J. L., Nakamura H. Desired speed distributions on two-lane highways under various conditions [J]. Transportati on Research Record, 2008，（2088）：218-226.

[4] 刘 岩，邵 岩. 城市快速路单车道车头间距的研究[J]. 大连交通大学学报，2012, 33(2): 20-22.

[5] 刘明君. 基于混合交通流的信号交叉口机动车车头时距研究[D]. 北京：北京交通大学，2010.

[6] 罗 霞，杜进有，霍亚敏. 车头间距分布规律的研究[J]. 西南交通大学学报，2011, 36（2）：113-116.

[7] 张智勇，黄 轶，任福田.稳定跟车状态车头间距分析方法[J].北京工业大学学报，2010，36(2): 219-222.

[8] 陆海亭，张 宁 等. 短时交通流预测方法研究进展[J]. 交通运输工程与信息学报，2009，7（4）：84-90.

[9] 孙 勇. 城市干道交通流运动状态特性研究[D].哈尔滨：哈尔滨工业大学，2007.

[10] 胡 路，蒲 云，蒋阳升 等. 城市轨道交通车站到达客流时间间隔分布拟合[J].系统工程理论与实践, 2014, 34（7）：1835-1845.

（中文编辑：吴继屏）

Analysis of Vehicle Arrival Law at Signalized Intersection

JIANG Yang-sheng1，2，3 HAN Shi-fan1，2，3 WU Ting1，2，3 ZHANG Gai4 1. National United Engineering Laboratory of Integrated and Intelligent Transportation， Chengdu 610031，China
2. Comprehensive Transportation Key Laboratory of Sichuan Province，Chengdu 610031，China
3. School of Transportation and Logistics， Southwest Jiaotong University， Chengdu 610031，China
4. Jiangsu Intelligent Transportation Systems Company，Nanjing 210000，China

Signalized intersection is an important node interrupted traffic flow， so，accurate description of the vehicle arrival law is an important factor affecting the intersection signal control design. The arrival vehicle at a signalized intersection is random and diverse， and obeys certain statistical regularity. In this paper， the arrival time interval of the traffic flow was statistically analyzed and fitted. The result showed that there was a coupling relation between the arrival traffic rule of signal intersection and square of its variation coefficient， the conclusions were as the following: the fitting of log normal distribution ranged from 0.8874 to 0.9904， the average fitness was up to 0.9489，having the best fitting effect； Gamma distribution fitting range was 0.5352 to 0.9449， 0.8056 was the average degree fitting， the fitting effect followed； the fitting of Weibull distribution was between 0.1997 and 0.8991， the average fitness was 0.616； The normal distribution fitting range was 0.2585 to 0.6671， and the average fitness was 0.6252；the exponential distribution fitting ranged from 0.0365 to 0.4077， the average fitting degree was 0.2317 and the fitting effect was the worst.

Signalized intersections， vehicle arrival laws， variation coefficients， headways

U491.2

A

1672-4747（2015）01-0001-06

10.3969/j.issn.1672-4747.2015.01.001

2014-03-22.

国家自然科学基金（项目编号：51108391和61170041）。

蒋阳升（1976-），男，汉族，湖南衡阳人，工学博士，西南交通大学教授，主要研究方向为交通信息化与智能化。