压缩感知曲线SAR孔径优化和目标三维特征提取*
何 峰,杨 阳,2,董 臻,梁甸农
(1.国防科技大学 电子科学与工程学院, 湖南 长沙 410073;
2.中国空气动力研究与发展中心, 四川 绵阳 621000)
压缩感知曲线SAR孔径优化和目标三维特征提取*
何 峰1,杨 阳1,2,董 臻1,梁甸农1
(1.国防科技大学 电子科学与工程学院, 湖南 长沙 410073;
2.中国空气动力研究与发展中心, 四川 绵阳 621000)
在建立曲线合成孔径雷达回波信号稀疏表示模型的基础上,基于压缩感知采样矩阵设计的不相关原则,给出了曲线孔径优化设计的评价准则,并利用基于全局优化的基追踪方法实现了目标三维特征提取。仿真结果验证了孔径优化评价准则的正确性和基追踪方法在目标特征提取处理中的有效性。
曲线合成孔径雷达;压缩感知;孔径设计;特征提取;基追踪;雷达三维成像
(1.CollegeofElectronicScienceandEngineering,NationalUniversityofDefenseTechnology,Changsha410073,China;
2.ChinaAerodynamicsResearchandDevelopmentCenter,Mianyang621000,China)
曲线合成孔径雷达(CurviLinearSyntheticApertureRadar,CLSAR)是一种工作在聚束方式下的新型微波对地观测技术,平台在方位-高度平面内作曲线飞行,在这两个方向同时形成分辨力,加上雷达宽带信号形成的距离分辨力,构成三维分辨能力,能提供更为丰富和全面的目标信息[1-2]。
优化的曲线孔径设计和有效的特征提取方法是CLSAR获取目标信息的关键。在曲线孔径优化设计上,现有方法或以参数估计的克拉美罗下限(CramerRaoLowerBound,CRLB)作为评价孔径性能的指标[3],或通过对各种孔径下目标特征提取性能的仿真[4-5],得到关于孔径设计的直观结论,尚缺乏基于三维图像重构性能的孔径设计原则和指导思想。现有的特征提取算法主要是基于谱估计理论的参数化RELAX方法[6]及其改进算法[7]。从信号表示理论的观点看,RELAX算法属于信号表示的吐故纳新算法,是迭代的局部优化型方法,原理上具有一定的先天局限性。
压缩感知(CompressedSensing,CS)是近年来出现的一种新理论[8-11]。本文将压缩感知理论运用到CLSAR孔径设计与三维图像重构中,在建立CLSAR回波稀疏信号模型的基础上,利用压缩感知理论在采样矩阵设计和信号重构方面的研究成果来解决曲线孔径设计和目标三维特征提取问题,通过仿真验证了本文所提方法的有效性。
1 CLSAR信号稀疏表示模型
如图1所示,雷达绕目标区域中心O作曲线运动,坐标系(x,y,z)以O点为原点,x,y,z轴分别表示方位、斜距和高度维。理论上,雷达运行轨迹可以是任意三维曲线,不过通常为减少距离维与方位-高度维的耦合,运行轨迹通常设计为平面曲线且所在平面平行于x-z面。Ro和R分别代表雷达到场景中心和坐标为(x,y,z)的一个散射点的距离;θ,φ分别代表雷达的方位角和俯仰角。

图1 曲线SAR工作几何图Fig.1 The geometry of CLSAR
对于CLSAR的观测对象,由几何绕射理论知[12],如果入射激励波的波长小于目标尺寸,目标的后向散射场可看成是由有限多个独立的散射中心的散射组成。以二维空间为例,单个散射中心的二维后向散射场可以描述为频率f和方位视角θ的函数,目标的散射场则是这些散射中心的合成[12]:
(1)
其中,σi为平均振幅,fc为中心频率,αi和γi分别描述每个散射中心散射强度对频率f和角度θ的依赖关系。式(1)表征了雷达目标后向散射场在频率-角度域的稀疏性,是基于压缩感知理论进行目标特征提取的理论基础。

(2)

(3)
假设有一个三维全孔径观测的虚拟系统,它在连续的二维视角变化下观测获得三维波数域的密集采样,则由式(3),该虚拟系统密集采样后的离散化回波可表示为如下矩阵形式:
x=ΨIsI
(4)

为构造完备基,我们将目标空间网格离散化,当网格间隔取波数域采样带宽的倒数时,无模糊成像范围内X,Y,Z方向上的目标网格数分别为Nx,Ny,Nz,假设每个空间网格都可能有目标(如无目标,则相应元素为0),按照与式(2)~(4)完全类似的方式重新推导,式(4)可以重新表示为:
x=ΨNsN
(5)
其中N=NxNyNz。对比式(4)、式(5),sN由I维扩展为NxNyNz维,全孔径观测数据x的维数与可分辨的最大目标数相等。ΨN是由三维的傅里叶基向量经Kronecker积后形成的完备基。由式(5)知全孔径下的图像重建就是三维傅里叶变换过程。由于目标区域内实际只分布了I个目标,因此sN是I-稀疏向量。

(6)
其中Indrow(·),Indcol(·)及Indlay(·)均为行列层索引算子,用于提取y中元素在原三维矩阵E中的行列层索引。则CLSAR稀疏观测模型可表示为:
y=Φ·x=Φ·ΨN·sN
(7)
式(7)中,目标的稀疏性表现在sN中只有I个有效元素,观测的稀疏性表现在Φ的行数M远远小于列数N。
根据CS理论,只要信号在某一个正交空间具有稀疏性,就能以较低的频率采样信号,并以高概率重构该信号。由式(5)、式(7)知,长度为N的全孔径信号x在完备的三维傅里叶基ΨN下的变换系数是I-稀疏的,如果用一个与ΨN不相关的观测基Φ:M×N对稀疏向量进行线性变换,并得到观测集合y:M×1。那么就可以利用优化求解方法从观测集合中高概率重构原始信号x或与之等价的sN。
2 曲线孔径优化
CLSAR观测数据是对全孔径回波的降维观测。根据压缩感知理论[8],信号重构的精度与采样矩阵和基矩阵的不相关度有关,两者不相关度越大,重构信号的精度越高。因此,应选择与三维傅里叶基矩阵ΨN不相关度最大的曲线孔径采样矩阵。本文引入文献[15]中定义的点散射函数(PointSpreadFunction,PSF)。原始的PSF函数形式是在一维傅里叶基下给出的[15],为了应用于CLSAR,重新定义PSF为
(8)
其中:ei表示一个N×1维向量,仅在第i个元素为1,Θ=Φ·ΨN,表示定义在三维波数空间的与Φ对应的采样子集上的三维傅里叶算子;Θ*表示Θ的伴随算子,即补零的傅里叶反变换。由定义知,PSF仅取决于曲线孔径确定的Φ,与目标特征、雷达参数等因素无关。在满足Nyquist采样定律的情况下PSF是一个单位阵。在欠采样情况下,将会使PSF矩阵中的非对角线元素非零,并使对角线元素幅度降低,意味着在重建中零元素受到原非零元素影响,它表征了非均匀欠采样造成的能量泄露。根据稀疏重构的原理,对目标特征提取性能影响最大的是峰值旁瓣,而非积分旁瓣。因此,泄露的旁瓣峰值能量越高,表示相关性越强,CLSAR孔径形状应使得这种能量泄露尽可能均匀地分布在图像中,避免产生较强的峰值。定义峰值不相关度(PeakDEcorrelation,PDE)为:
(9)
不相关度越大,则该孔径形状下欠采样得到的观测数据重建的收敛性能越好,旁瓣越小。表1给出了几种典型曲线轨迹的不相关度(方位-高度全采样矩阵大小为50×50,其中抛物线、sin曲线、三角折线为50个采样点,圆和垂直折线为100个采样点)。

表1 典型曲线孔径的不相关度
由表1知,全孔径的不相关度为1,对目标特征提取的精度和算法收敛性最好。在给出的几种孔径中,抛物线具有最高的不相关度,说明多项式曲线可以作为一种较好的采样轨迹。在已有研究中,文献[3]将参数估计的CRLB作为评价孔径性能的指标,得出的结论为大尺寸、非线性程度越高的孔径具有更优的估计性能;文献[5]通过直观比较典型非直线孔径录取数据的成像性能发现,在相同的孔径跨度范围上,抛物线形孔径具有比折线形孔径更优的成像性能。由此可见,本文利用不相关度指标PDE得出的结论与已有文献中的结论是相符的。
3 目标三维特征提取
目前CLSAR处理普遍采用基于最小化非线性方差准则的RELAX算法,能有效降低目标旁瓣,但存在稳健性问题,且需要估计散射点的个数。从信号表示的观点看,RELAX算法实际上是匹配追踪(MatchPursuit,MP)和交替尺度法相结合的产物,能在一定程度上克服匹配追踪的弱点,但仍然脱离不了吐故纳新算法的范畴,具有短视效应,很多情况得不到全局最优解。基于度量函数的全局竞争优化算法则避免了吐故纳新类算法固有的贪婪和短视行为,具有原理上的优越性。基追踪(BasisPursuit,BP)[10]作为一种全局优化策略考虑如下的(P1)问题:
(P1)min‖s‖1sub.y=Θ·s
(10)
它可以等价为一个线性规划问题,如果问题的解满足一定的稀疏条件[16],则可用单纯形法或内点法求解。作为一种全局优化算法,BP方法具有更好的稳健性和收敛性能,可在相当宽泛的条件下获得信号表示的稀疏解,并且它不需要已知散射点个数,便于在实际中实现。
4 仿真实验
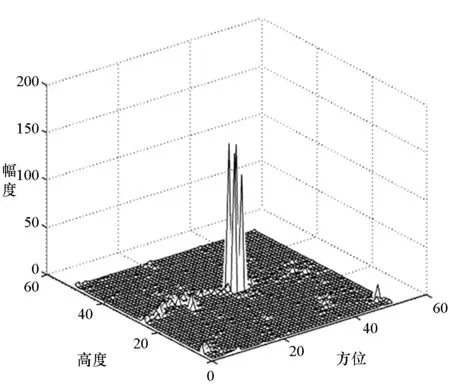
设信号带宽为1GHz,曲线孔径在高度向和方位向各有50个观测角,在斜距向有50个采样点。首先仿真场景中心单点目标在抛物线孔径下通过快速傅里叶变换(FastFourierTransformation,FFT)重建和BP重建的对比,其方位-高度维幅度图如图2所示。可见,BP方法在有效提取目标峰值的同时可以大大降低旁瓣。

(a) FFT重建(a) FFT reconstruction

(b) BP重建(b) BP reconstruction图2 抛物线孔径下目标FFT重建和BP重建对比Fig.2 Comparison between FFT method and BP method in parabola aperture
针对由四个三维空间分布的散射点组成的目标进行重建仿真,四个散射点散射强度相等,满足远场观测条件。目标的真实分布如图3所示,其中圆心代表目标在场景中的位置,半径表示散射强度(下同)。
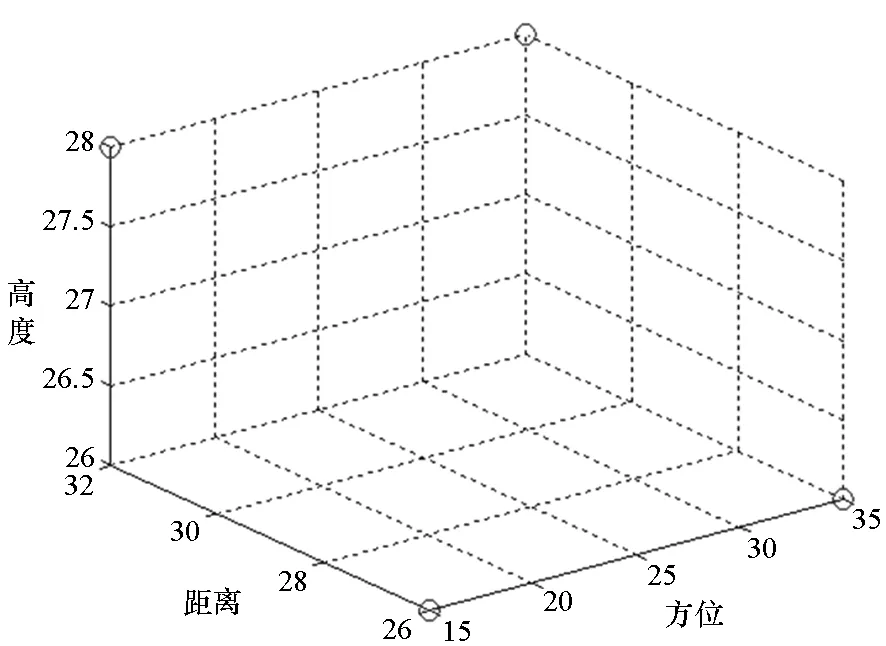
图3 目标真实分布图Fig. 3 Target distribution
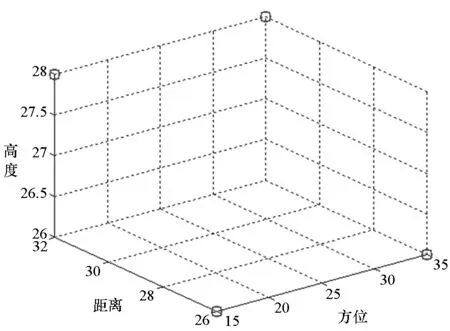
图4 全孔径下目标特征提取Fig.4 Target feature extraction in full aperture

图5 抛物线孔径下目标特征提取Fig.5 Target feature extraction in parabola aperture
在全孔径观测下,对目标进行估计的结果如图4所示,四个散射点均能得到位置和幅度的准确估计。根据表1列出的几种曲线,选择抛物线和圆作为曲线孔径进行仿真,BP重建得到的结果如图5和图6所示。可见,与全孔径相比,在抛物线孔径和圆孔径情况下,BP方法均能够准确地估计出目标位置,但是信号的幅度会有不同程度的衰减,其中圆孔径下幅度的衰减更加严重。图5和图6还画出了重构后大于目标幅度10%的旁瓣,可以看出圆孔径下远端目标各产生了一个虚假目标,而抛物线孔径下则没有虚假目标。这一仿真结果与表1中利用PDE指标的性能评价结果一致。
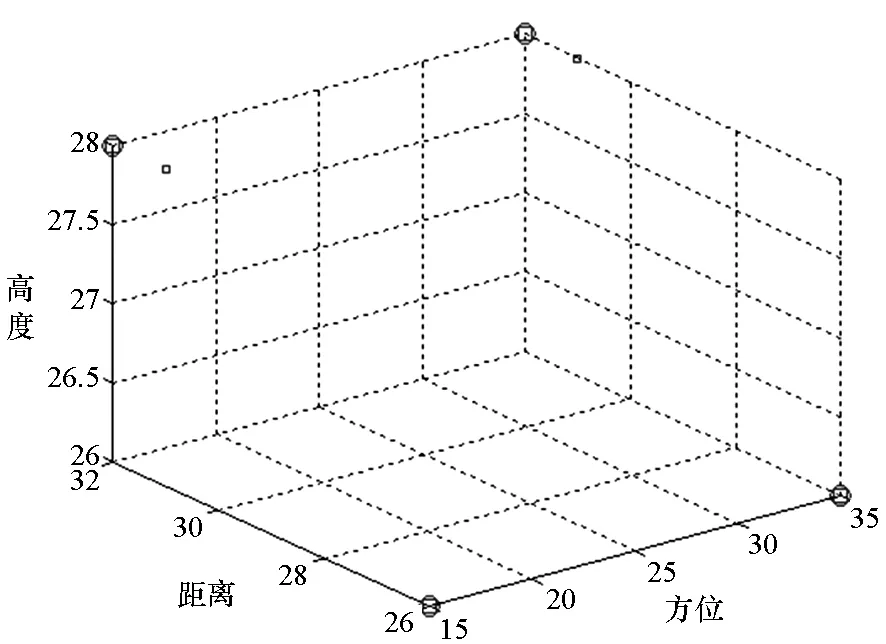
图6 圆孔径下目标特征提取Fig.6 Target feature extraction in circle aperture

(a) BP:抛物线孔径(a) BP: parabola aperture

(b) RELAX:抛物线孔径(b) RELAX: parabola aperture

(c) BP:圆孔径(c) BP: circle aperture图7 抛物线和圆孔径下基追踪和RELAX方法提取的目标方位-高度维幅度Fig.7 Target intensity in azimuth-height dimensions based on BP and RELAX
在方位-高度采样网格点(26,26),(26,28),(28,26)和(28,28)四个位置分别设置幅度为100的点目标,在抛物线和圆孔径条件下应用BP方法和RELAX算法对目标进行特征提取。图7给出了在无噪声下两种方法提取的目标方位-高度维幅度,其中图7(a)、(c)为BP方法计算结果,图7(b)为RELAX方法计算结果,在圆孔径下,RELAX方法的解无法收敛。从图7可以看出,对不同位置的目标,BP方法能够在给出的两种孔径下准确提取出目标位置,目标幅度有所下降,但其在四个位置上幅度差异不大;RELAX算法能够准确提取出抛物线孔径下目标位置信息,但对目标幅度的估计不稳健,在圆孔径下无法收敛到稳定解。可见相比于RELAX算法,BP算法更稳健。
(a) BP:信噪比为0dB(a)BP: SNR =0dB
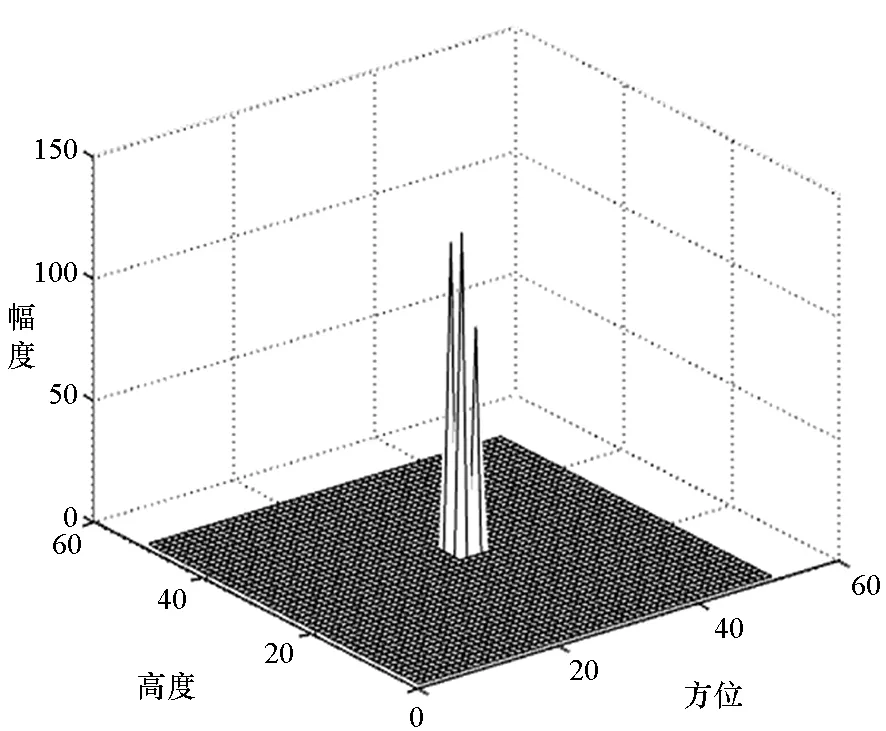
(b) RELAX:信噪比为0dB(b)RELAX:SNR=0dB
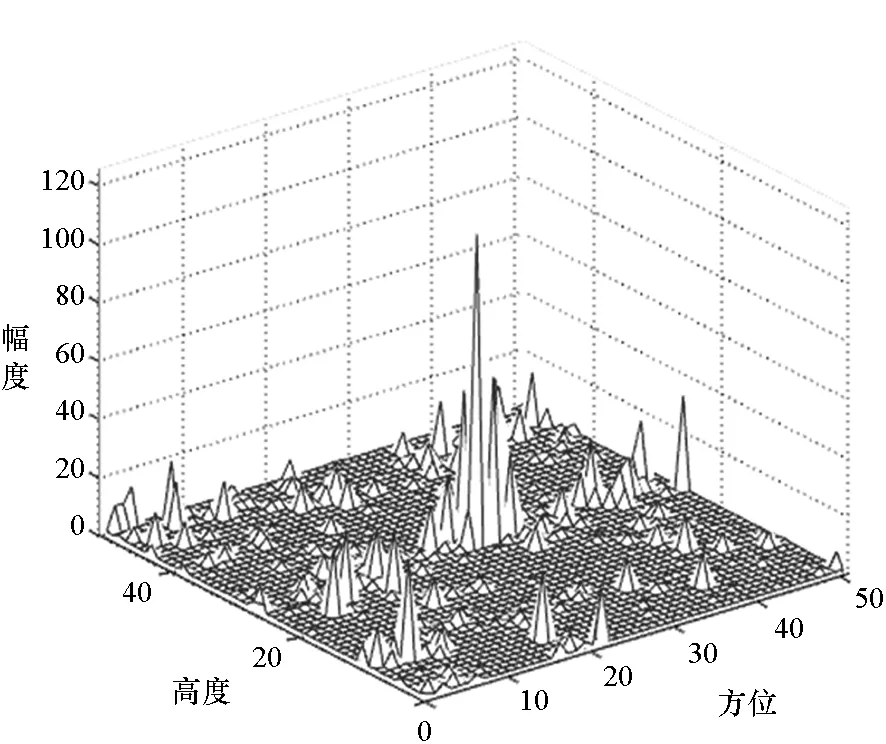
(c) BP:信噪比为-10dB(c) BP: SNR =-10dB图8 抛物线孔径下叠加高斯白噪声后,用BP和RELAX提取的目标方位-高度维幅度Fig.8 Target intensity in azimuth-height dimensions based on BP and RELAX with adding Gaussian white noise
图8为抛物线孔径下对信号叠加不同能量的高斯白噪声后,运用BP方法和RELAX算法进行特征提取的结果。在信噪比为0dB情况下,两者均能准确提取出目标位置信息。当继续加大噪声能量,使信噪比为-10dB时,尽管存在较多旁瓣,但BP方法仍能准确提取出四个目标的位置,而RELAX算法则不能收敛到稳定解。仿真说明了BP方法在强噪声环境下,具有更好的稳健性。
5 结论
本文提出了基于压缩感知理论的曲线SAR三维目标特征提取方法和曲线孔径优化评价方法。在对曲线SAR进行目标回波稀疏表示建模的基础上,从压缩感知理论采样矩阵不相关原则出发,通过定义峰值不相关度这一不相关度量,指导了曲线孔径的优化问题;利用BP算法这一全局最优的稀疏表示寻优方法实现了目标的特征提取,取得了较好的效果。仿真验证了本文方法的有效性。
References)
[1] 张子善. 曲线合成孔径雷达三维成像相关技术研究[D]. 长沙:国防科学技术大学,2009.
ZHANGZishan.ResearchonkeytechnologiesofcurvilinearSAR3-dimentionalimaging[D].Changsha:NationalUniversityofDefenseTechnology, 2009.(inChinese)
[2] 洪文. 圆迹SAR成像技术研究进展[J]. 雷达学报,2012,1(2): 124-135.HONGWen.ProgressincircularSARimagingtechnique[J].JournalofRadars, 2012, 1(2): 124-135.(inChinese)
[3]SuZG,PengYN,WangXT.Feature-independentapertureevaluatorforthecurvilinearSAR[J].IEEEGeoscienceandRemoteSensingLetters, 2007, 4(2):191-195.
[4]TangZ,LiJW,ZhouYQ,etal.ResearchonoptimalapertureforcurvilinearSAR[J].JournalofAstronautics, 2006, 27(5):898-903.
[5]BrianDR,RandolphLM.Flightpathstrategiesfor3DscenereconstructionfrombistaticSAR[J].IEEProceedings-Radar,SonarandNavigation, 2004, 151(3): 149-157.
[6]LiuZS,KnaellK.UseofcurvilinearSARforthreedimensionaltargetfeatureextraction[J].IEEProceedingsofRadar,SonarandNavigation, 1997, 144(5): 275-283.
[7]LiJ,BiZ,LiuZS.AutofocusandfeatureextractionincurvilinearSARviaarelaxation-basedalgorithm[J].IEEProceedingsofRadar,SonarandNavigation, 1999, 146(4): 201-207.
[8]DonohoDL.Compresssensing[J].IEEETransactionsonInformationTheory, 2006,52(4):1289-1306.
[9]BaraniukR.Alectureoncompressivesensing[J].IEEESignalProcessingMagazine, 2007, 24(4):118-121.
[10]ChenSS,DonohoDL,SaundersMA.Atomicdecompositionbybasispursuit[J].SIAMReview, 2001,43(1):129-159
[11] 叶钒,何峰,梁甸农,等. 基于压缩感知的多频率信号融合[J]. 国防科技大学学报,2010,32(4):84-87.
YEFan,HEFeng,LIANGDiannong,etal.Multi-frequencyfusionbasedoncompressivesensing[J].JournalofNationalUniversityofDefenseTechnology,2010,32(4):84-87.(inChinese)
[12]GerryMJ,PrincipeLC,etal.Aparametricmodelforsyntheticapertureradarmeasurements[J].IEEETransactionsonAntennasandPropagation, 1999, 47(7):1179-1188.
[13]VannLD,CuomoKM,PiouJE,etal.Multisensorfusionprocessingforenhancedradarimaging:technicalreport1056oflincolnlab[R].Lexington,MA:MassachusettsInstituteTechnology, 2000.
[14]CaputiWJ.Stretch:atime-transformationtechnique[J].IEEETransactionsonAerospaceandElectronicSystems, 1971, 7(2): 269-278.
[15]LustigM.CompressedsensingMRI[J].IEEESignalProcessing, 2008, 24(2): 72-82.
[16]DonohoDL,EladM.Optimallysparserepresentationingeneraldictionariesvial1minimization[J].PNAS, 2003, 100(5): 2197-2202.
Aperture optimizing and 3-dimensional target feature extraction of curvilinear SAR based on compress sensing
HE Feng1, YANG Yang1, 2, DONG Zhen1, LIANG Diannong1
Thecompressedsensingtheorywasappliedtocurvilinearapertureoptimizingand3-dimentionaltargetfeatureextractionofcurvilinearsyntheticapertureradar.First,theechosignaltargetsparserepresentationmodelwasbuilt.Basedontheincoherenceprinciplebetweensparsematrixandsamplingmatrixofthecompressedsensingtheory,aguidelineofevaluationtocurvilinearapertureoptimizingwasfound.Moreover,the3-dimentionaltargetfeatureextractionwasrealizedbyemployingthebasispursuitmethod.Simulationresultsprovethecorrectnessoftheapertureoptimizationstrategieswiththeincoherenceprincipleaswellastheefficiencyofthebasispursuitmethodintargetfeatureextraction.
curvilinearsyntheticapertureradar;compressedsensing;aperturedesign;featureextraction;basispursuit;radar3-dimensionalimaging
2014-10-27
国家自然科学基金资助项目(61101187)
何峰(1976—),男,湖北孝感人,副研究员,博士,硕士生导师,E-mail:hefeng@nudt.edu.cn
10.11887/j.cn.201504016
http://journal.nudt.edu.cn
TN
A

