临近空间大型柔性充气囊体结构特性分析*
麻震宇,侯中喜,杨希祥
临近空间大型柔性充气囊体结构特性分析*
麻震宇,侯中喜,杨希祥
(国防科技大学 航天科学与工程学院, 湖南 长沙 410073)
以临近空间平流层飞艇柔性充气囊体为研究对象,根据充气结构设计理论对充气囊体结构的最小压差和应力进行计算,建立平流层飞艇充气囊体结构有限元模型。在模型验证的基础上,采用非线性有限元方法对平流层飞艇充气囊体结构特性进行仿真分析,得到了囊体结构在不同压差和吊舱载荷作用下应力和变形分布及变化规律,并分析了结构加强配置对囊体应力和变形的影响,为平流层飞艇结构设计提供技术支撑和参考依据。
平流层飞艇;柔性充气结构;非线性有限元方法;结构特性
(CollegeofAerospaceScienceandEngineering,NationalUniversityofDefenseTechnology,Changsha410073,China)
平流层飞艇是工作在临近空间的新型平台,具有驻空时间长、成本低和分辨率高等优点,在对地观测、导弹预警、通信导航等方面有广阔的应用前景和重要的军事价值[1]。平流层飞艇体积巨大,依靠内部填充的浮升气体产生净浮力,是一种典型的大型柔性充气结构。目前相关试验研究表明,在没有特殊调控措施的情况下,平流层飞艇驻空飞行期间囊体内部气体超热可达20℃至70℃,而气体超热程度直接影响囊体的超压程度,对囊体结构强度和安全性提出严重挑战。同时,气动载荷、吊舱载荷等复杂的载荷工况也对飞艇囊体结构性能产生重要影响。
柔性充气囊体是平流层飞艇的结构主体,其结构特性分析是平流层飞艇总体设计的研究基础。Liao等[2]总结了不同类型飞艇结构布局发展现状,并对飞艇囊体结构的外形优化进行了综述。Rehmet等[3]对太阳能高空长期驻空飞艇平台总体结构设计开展了研究,针对飞艇囊压特性进行了分析,提出了多节囊体结构的概念。Smith等[4]对HiSentinel系列飞艇开展了大量研究,为平流层飞艇的结构设计提供了参考。陈务军、高海健等[5-9]基于无矩薄壳理论和虚功原理推导了飞艇柔性囊体结构应力和变形计算公式,为飞艇囊体结构的设计提供了重要理论依据。席俊波[10]考虑几何非线性影响,采用薄板单元模拟了飞艇在不同工况下的承载性能。杨留义[11]对飞艇柔性充气囊体结构的变形及应力分布进行计算,得到了考虑吊舱重量及等效风载下囊体结构的变形和响应。黄迪等[12]利用ANSYS仿真分析得到飞艇囊体蒙皮各点受力情况,将理论应力值与有限元结果进行对比,验证了飞艇囊体应力估算的准确性。刘龙斌等[13]采用ABAQUS计算得到飞艇囊体蒙皮分别在不同超压载荷下的应力分布情况,为囊体蒙皮超压应力评估和强度计算提供参考。谭惠丰等[14-15]研究发现通过改变飞艇结构形式可提高结构性能,汪逸然[16]提出在飞艇囊体中布置一定数量的增强索系,可提高充气囊体结构的承载能力。综上所述,当前对于平流层飞艇囊体结构特性分析与设计还处于探索阶段。
1 理论分析
1.1 囊体最小压差计算
Fodaro等[17]以囊体头部不出现局部内陷为原则,综合考虑局部静压、囊体动压及浮升气体重力梯度等三个方面,给出了囊体所需的最小囊压计算方法。囊体静态压差为:
(1)
式中,1.15为飞艇囊压设计修正系数,u为来流风速。
在给定工作高度的动态工作压差为:
(2)
式中,Cp为无量纲压力系数,其取值范围一般为0.3~0.35。
重力作用引起的静水压力梯度为:
(3)
式中,d为囊体的最大截面直径。
将式(1)~(3)相加可得到囊体最小压力计算公式。在平流层飞艇实际飞行过程中,考虑到附加结构等引起的局部变形和应力集中现象,工作囊压水平将高于囊体最小压差。
1.2 囊体应力计算
平流层飞艇囊体一般为旋转体,轴向长度约为最大截面直径的4倍左右,对于无附加结构的囊体中间直线段,蒙皮应力计算公式为:
(4)
式中:σa和σr分别为飞艇蒙皮的轴向应力和环向应力;p为囊体内外压差;r(x)为沿轴向x处囊体截面半径;t为囊体蒙皮厚度。根据式(4),囊体中间直线段轴向应力大小为环向应力大小的一半,且最大应力出现在囊体截面半径最大处。通常采用VonMises等效应力对囊体蒙皮强度进行分析评估,其计算公式为:
(5)
式中:σ1,σ2和σ3分别为第一、第二和第三主应力。根据蒙皮薄膜结构受力特点,σ1=σr,σ2=σa,σ3=0。
2 数值分析
2.1 有限元模型
基于有限元软件ANSYS对平流层飞艇充气囊体结构特性进行仿真分析。以美国高空飞艇(HighAltitudeAirship,HAA)的几何外形作为参考对象,如图1所示,其中飞艇长度为152.40m,最大截面半径为21.87m。采用八节点四边形壳单元SHELL281建立平流层飞艇囊体有限元模型,仅保留单元的薄膜刚度以模拟飞艇囊体的薄膜特性。为更准确得到囊体应力和变形情况,在飞艇头部和尾部附近细分网格,飞艇囊体结构有限元网格划分如图2所示。囊体蒙皮材料假设为各向同性材料,弹性模量取值为E=4GPa,泊松比为μ=0.38,蒙皮厚度取t=0.4mm。在边界条件设置方面,头部节点约束除轴向之外的其余自由度,只允许轴向位移;尾部节点约束全部自由度,模拟固支。分析结构受力情况,作用在囊体上的力包括压差载荷和吊舱载荷,其中压差载荷作为面力均匀施加于囊体蒙皮内表面,吊舱载荷简化为集中力等效施加于囊体吊舱处节点。计算过程采用非线性静态分析,考虑大变形和应力刚化效应,采用牛顿-拉普森线性搜索算法进行求解。

图1 高空飞艇几何示意图Fig.1 Structural diagram of the HAA

图2 平流层飞艇有限元模型Fig.2 Finite element model of the HAA
2.2 模型验证
文献[7]采用理论和数值仿真方法对悬臂充气梁结构的承载性能进行了计算分析。为验证本文有限元模型及计算方法的准确性,将计算结果与文献理论计算结果进行比较。其中,充气梁长度2000mm,直径400mm,膜材弹性模量0.706 39GPa,泊松比0.38,厚度0.482mm,在距固定端1800mm处作用垂直向下的载荷。采用SHELL281单元建立充气梁有限元模型,如图3所示。表1给出了不同工况下充气梁端挠度的计算结果对比。如表所示,本文计算结果与文献理论计算值之间的误差均在10%以内,验证了有限元模型和计算方法的合理性。

(a) 充气梁结构有限元模型(a) Finite element model of inflatable beam

(b) 充气梁结构垂直方向位移云图(b) Displacement contour of inflatable beam in vertical图3 充气梁结构算例示意图Fig.3 Sketch of inflatable beam model

计算工况F=65N梁端挠度/mm计算结果文献理论值误差气压10kPa17.22715.69.4%气压50kPa16.1714.88.5%气压100kPa15.91414.77.6%
2.3 计算结果
2.3.1 超压特性分析
根据式(1)~(3)得到HAA飞艇囊体最小压差理论值为150.7Pa,考虑囊体内部附加结构等集中力作用,囊体的工作压差会远高于理论水平。假设飞艇驻空高度为20km,囊体内部气体超热为40℃,根据理想气体状态方程可得到囊体内外压差达到约2000Pa,将可能导致囊体胀裂破坏。在模型验证的基础上,囊体内外压差在200~2000Pa范围内变化,对不同压差载荷下的囊体结构特性进行计算分析。
图4给出了压差为800Pa时的囊体结构等效应力云图和等效变形云图。如图所示,飞艇囊体应力分布沿轴向规律变化,在截面最大直径处应力值最大,沿轴向递减,在头、尾部应力最小,与理论分析结论一致;囊体变形分布与应力相同,在截面最大直径处变形量最大。

(a) 等效应力云图(a) Contour of equivalent Von Mises stress

(b) 等效位移云图(b) Contour of equivalent displacement图4 压差800Pa计算结果Fig.4 Computational results of differential pressure of 800Pa
图5给出了囊体最大第一主应力、最大等效应力和最大位移随压差变化曲线。如图所示,随着内外压差的提高,囊体应力值和变形量呈近似线性递增。当压差为200Pa时,最大等效应力值为8.9MPa,最大等效位移为0.057m;当压差为2000Pa时,最大等效应力值达到91.7MPa,最大等效位移为0.558m,压差载荷对囊体结构安全性影响较大。囊体应力值结果与理论公式计算结果吻合,进一步验证了数值模型的准确性。

(a) 应力变化曲线(a)Stress results under different pressure loads

(b) 位移变化曲线(b) Displacement results under different pressure loads图5 应力和变形随压差变化曲线Fig.5 Change curves of stress and deformation under different pressure loads
2.3.2 承载特性分析
最大有效载荷重量是飞艇的重要性能指标,提高飞艇载重也是平流层飞艇的发展趋势。以内外压差作为预应力,得到囊体充压状态,在模型节点几何更新的基础上,施加吊舱载荷值在5000~25000N范围内变化,对不同吊舱载荷下的囊体结构特性进行计算分析。

(a) 等效应力云图(a) Contour of equivalent VonMises stress

(b) 等效位移云图(b) Contour of equivalent displacement图6 吊舱载荷10000N计算结果Fig.6 Results of gondola load of 10000N
图6给出了压差800Pa、吊舱载荷为10000N时的囊体结构等效应力云图和等效位移云图。如图所示,在吊舱处出现应力集中现象,等效应力值远远大于囊体其他部位应力,且吊舱处的变形最大,位移值显著大于周围结构蒙皮。
图7给出了压差载荷为800Pa时,最大等效应力和最大等效位移随吊舱载荷的变化曲线。如图所示,随着吊舱载荷的提高,囊体应力和变形呈近似线性递增。当吊舱载荷为5000N时,最大等效应力值为38.7MPa,最大等效位移为0.097m;当吊舱载荷为25000N时,最大等效应力值达到49.1MPa,最大等效位移为0.418m,吊舱载荷对囊体结构特性影响较大。

(a) 应力变化曲线(a) Stress results under different gondola loads
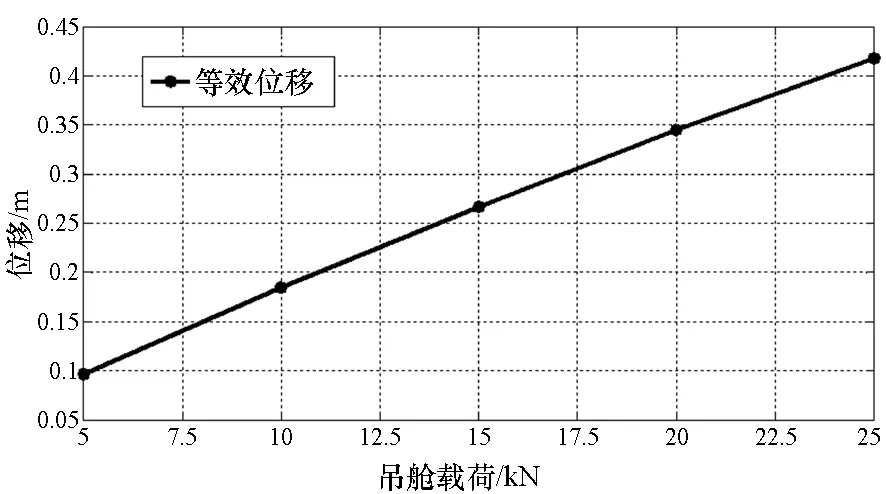
(b) 位移变化曲线(b) Displacement results under different gondola loads图7 应力和变形随吊舱载荷变化曲线Fig.7 Change curves of stress and deformation under different gondola loads
图8给出了吊舱载荷为10 000N时,囊体最大等效应力和最大等效变形随压差的变化曲线。如图所示,随着内外压差的提高,囊体应力呈线性增长,但囊体变形大幅度减小。这是因为内外压差的增大使充气囊体的整体刚度提高,结构变形减小。

(a) 应力变化曲线(a) Stress results under different pressure loads
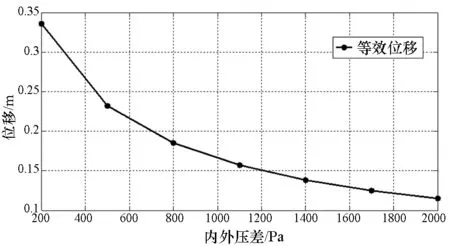
(b) 位移变化曲线(b) Displacement results under different pressure loads图8 吊舱载荷10000N时应力和变形随压差变化曲线Fig.8 Change of stress and deformation with differential pressure under gondola loads of 10000N
2.3.3 结构加强配置分析
采用纵向和环向绳索布置对飞艇囊体结构进行加强处理,纵向加强配置包括在囊体下腹部配置1根加强索和沿环向均匀布置4根加强索;环向加强配置为分别沿轴向布置3根和7根加强索。绳索弹性模量取值E=100GPa,泊松比μ=0.3,直径d=2~8mm。

(a) 等效应力云图(a) Contour of equivalent Von Mises stress

(b) 等效位移云图(b) Contour of equivalent displacement图9 结构纵向和环向加强配置计算结果Fig.9 Results of vertical and ring stiffened confirguration
图9给出了压差800Pa、吊舱载荷10 000N、绳索直径5mm时,采用4根纵向加强索和7根环向加强索的囊体结构等效应力云图和等效位移云图。图10给出了采用不同加强索数量布置的囊体最大等效应力和最大等效位移变化曲线,图11给出了采用4根纵向加强索索和7根环向加强索的囊体最大等效应力和最大等效变形随绳索直径尺寸变化曲线。由图所示,采用纵向和环向加强配置可显著提高囊体结构性能,囊体最大等效应力值减小约12%,最大等效位移值减小约38%;但随着纵向和环向加强索数量和尺寸的增加,应力和变形减小幅度渐小,结构性能提升幅度有限,需要进一步对加强配置进行优化设计。

(a) 应力变化曲线(a) Stress results under different ring stiffeners
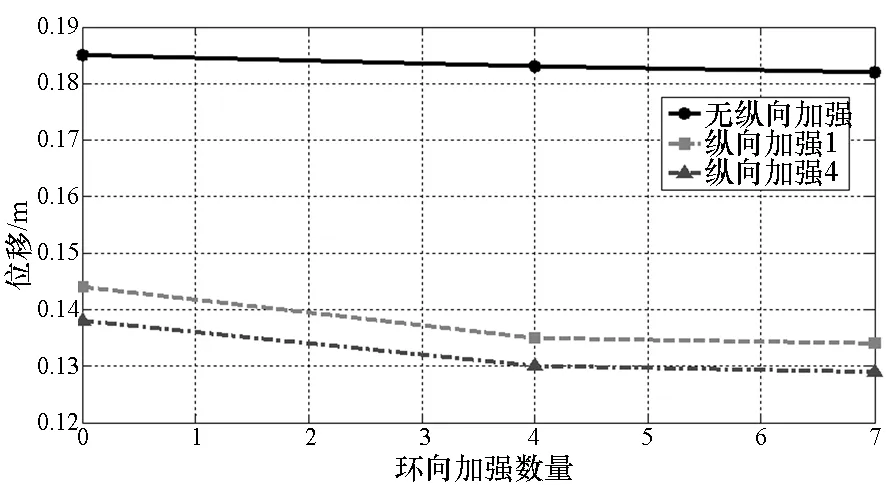
(b) 位移变化曲线(b) Displacement results under different ring stiffeners图10 不同加强配置结构应力和变形变化曲线Fig.10 Results under different stiffened confirgurations

(a) 应力变化曲线(a)Stress results under different diameters of stiffener
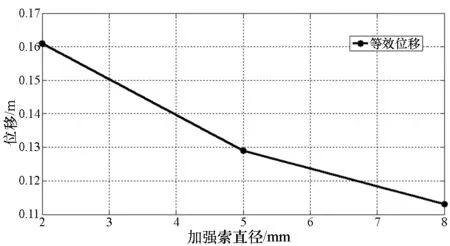
(b) 位移变化曲线(b) Displacement results under different diameters of stiffener图11 应力和变形随绳索直径尺寸变化曲线Fig.11 Results under different diameters of stiffener
3 结论
随着内外压差和吊舱载荷的提高,囊体应力值和变形量呈近似线性增长;采用纵向和环向加强配置可显著提高囊体结构性能,囊体最大等效应力值和最大等效位移减小幅度分别可达12%和38%,但随着纵向和环向加强索数量和尺寸的增加,结构性能提升幅度有限,需进一步开展结构优化设计研究。
References)
[1]FesenRA.Ahigh-altitude,station-keepingastronomicalplatform[C]//ProceedingsofAstronomicalTelescopesandInstrumentation, 2006: 6-8.
[2]LiaoL,PasternakI.Areviewofairshipstructuralresearchanddevelopment[J].ProgressinAerospaceSciences, 2009,45(4):83-96.
[3]RehmetMA,KröplinBH,EpperleinF,etal.Recentdevelopmentsonhighaltitudeplatforms[C]//Proceedingsof3rdInternationalAirshipConventionandExhibition, 2000:B-8.
[4]SmithISJr,LeeM.ThehiSentinelairship[C]//Proceedingsof7thAIAAAviationTechnology,IntegrationandOperationsConference,AIAA2007-7748, 2007.
[5]ChenWJ,XiaoWW,KröplinB,etal.StructuralperformanceevaluationprocedureforlargeflexibleairshipofHALEstratosphericplatformconception[J].JournalofShanghaiJiaotongUniversity(Science), 2007,E-12(2): 293-300.
[6] 高海健, 陈务军, 付功义, 等. 平流层平台柔性飞艇结构弹性分析理论[J]. 上海交通大学学报, 2010,44:1583-1587.
GAOHaijian,CHENWujun,FUGongyi,etal.Structuralanalysisorientedengineeringelastictheoryforflexibleairshipofstratosphericplatform[J].JournalofShanghaiJiaotongUniversity, 2010, 44( 11) : 1583-1588.(inChinese)
[7] 高海健. 大型平流层平台柔性飞艇结构分析理论与特性研究[D]. 上海:上海交通大学, 2010.
GAOHaijian.Structuralanalysistheoryandperformance
researchforlargeflexibleairshipofstratosphericplatform[D].Shanghai:ShanghaiJiaotongUniversity, 2010.(inChinese)
[8] 高海健,陈务军,付功义.平流层验证飞艇结构体系比较研究[J].宇航学报, 2011, 32(4): 713-720.
GAOHaijian,CHENWujun,FUGongyi.Comparisoninvestigationforarchitectureofstratosphericdemonstrationairship[J].JournalofAstronautics, 2011, 32(4): 713-720.(inChinese)
[9] 高海健, 陈务军, 付功义, 等. 考虑气压效应平流层平台柔性飞艇变形分析方法与特征研究[J]. 应用力学学报, 2012, 29(4): 374-379.
GAOHaijian,CHENWujun,FUGongyi,etal.Deformationanalysismethodandperformanceevaluationforflexibleairshipofstratosphericplatformconsideringpressureeffects[J].ChineseJournalofAppliedMechanics, 2012, 29(4): 374-379.(inChinese)
[10] 席俊波. 飞艇囊体几何非线性有限元分析[D]. 西安:西北工业大学, 2006.
XIJunbo.Nonlinerfiniteelementanalysisofairshipenvelope[D].Xi’an:NorthwesternPolytechnicalUniversity, 2006.(inChinese)
[11] 杨留义. 囊体结构设计及其气弹特性计算分析[D]. 哈尔滨:哈尔滨工业大学, 2012.
YANGLiuyi.Structuraldesignandnumericalaeroelasticanalysisofairshipenvelope[D].Harbin:HarbinInstituteofTechnology, 2012.(inChinese)
[12] 黄迪, 赵海涛, 邱野,等. 平流层飞艇蒙皮强度建模与仿真研究[J]. 计算机仿真, 2013, 30(1):150-153.
HUANGDi,ZHAOHaitao,QIUYe,etal.Modelingandsimulationanalysisofstratosphericairshipenvelope[J].ComputerSimulation, 2013, 30 (1) :150-153.(inChinese)[13] 刘龙斌, 吕明云, 肖厚地, 等. 基于压差梯度的平流层飞艇艇囊应力计算和仿真[J]. 北京航空航天大学学报, 2014, 4(1): 1-6.
LIULongbin,LYUMingyun,XIAOHoudi,etal.Calculationandsimulationofstratosphericairshipcapsulestressconsideringthepressuregradient[J].JournalofBeijingUniversityofAeronauticsandAstronautics, 2014, 4(1): 1-6. (inChinese)
[14] 谭惠丰, 王超, 王长国. 实现结构轻量化的新型平流层飞艇研究进展[J]. 航空学报, 2010, 31(2): 257-264.TANHuifeng,WANGChao,WANGChangguo.Progressofnewtypestratosphericairshipsforrealizationoflightweight[J].ActaAeronalticaetAstronalticaSinica, 2010, 31(2): 257-264.(inChinese)[15] 谭惠丰, 孟松鹤, 王超. 新型空中展开飞艇[C]//2007年中国浮空器大会论文集, 北京, 2007: 17-21.
TANHuifeng,MENGSonghe,WANGChao.Anewtypedeployableairship[C]//ProceedingsofAerostatConferenceofChina2007,Beijing, 2007: 17-21.(inChinese)
[16] 汪逸然. 系绳增强充气结构承载性能分析[D]. 哈尔滨:哈尔滨工业大学, 2013.
WANGYiran.Bearingcapacityanalysisofinflatablestructureswithenhancingtethers[D].Harbin:HarbinInstituteofTechnology, 2013.(inChinese)
[17]FodaroD.Employofthepneumaticstructuresintheunconventionalairshipdesign[C]//ProceedingsofAIAABalloonSystemsConference,AIAA2007-2628, 2007.
Structural performance analysis of large-scale flexible inflatable structures for stratospheric airships
MA Zhenyu, HOU Zhongxi, YANG Xixiang
Takinginflatablestructuresofstratosphericairshipsasthemainstudyobject,theminimumdifferentialpressureandthestressofinflatablestructureswerecomputedaccordingtoitsdesigntheoryandafiniteelementmodelofinflatablestructureforstratosphericairshipwasestablished.Onthebasisofthemodelverification,nonlinearfiniteelementmethodwasappliedtosimulateinflatablestructuralperformancesoastoobtainthedistributionandchangelawsofthedeformationsandstressesofinflatablestructurewiththevariationsofpressureloadandgondolaload.Theeffectsofstructuralreinforcementdevicesonthestressanddeformationofinflatablestructurealsowereevaluated.Thesimulationresultscanserveasreferenceforthestructuraldesignofthestratosphericairship.
stratosphericairship;flexibleinflatablestructures;nonlinearfiniteelementmethod;structuralperformance
2015-04-20基金项目:国家高分重大专项支持资助项目(GFZX040201)
麻震宇(1982—),男,河南洛阳人,讲师,博士,E-mail:mazhenyu@nudt.edu.cn
10.11887/j.cn.201504005
http://journal.nudt.edu.cn
V
A

