适用于临近空间飞行器大变形的动网格策略*
柳兆伟,侯中喜,陈立立
适用于临近空间飞行器大变形的动网格策略*
柳兆伟,侯中喜,陈立立
(国防科技大学 航天科学与工程学院, 湖南 长沙 410073)
对于超大展弦比构型的低速临近空间飞行器而言,由于其在飞行过程中结构变形非常显著,因此基于计算流体力学的分析方法对于动网格提出了非常高的要求。为此,提出了一种适用于边界大变形的动网格策略,该种动网格基于映射的思想,将边界网格的位置变化以某种权重反映到流场网格,并更新网格节点位置。选取距离倒数的n次方作为权重,研究不同的权重指数n对网格变形的影响规律,然后开展了二维与三维动网格实例分析。结果表明,这种动网格方法能够很好地适用于大变形的情形,并能很好地保证变形后的网格质量。
动网格;大变形;变形策略
(College of Aerospace Science and Engineering, National University of Defense Technology, Changsha 410073, China)
在军用和民用领域巨大需求的牵引下,高空长航时(High Altitude Long Endurance,HALE)飞行器得到快速的发展,特别的以“太阳神”[1]“微风”“阳光动力”等为代表的一系列太阳能飞机的发展,大大促进了该技术的提升。如图1所示,展示了几种高空长航时太阳能飞行器。为了实现高空长航时这一目标,该类型飞行器结构面密度通常较低,由此导致刚度明显不足,在飞行过程中受到气动载荷时,结构变形非常显著,同时结构变形又使得气动性能发生改变,因而结构与气动出现较强耦合。

图1 高空长航时大展弦比飞行器Fig1 HALE high-aspect-ratio aircrafts
近年来,基于计算流体力学的流固耦合分析方法得到快速的发展与广泛的应用[2-6]。这种方法要求结构和气动两个学科独立建模,并采用交错求解的方式进行计算。流体计算中一般采用基于空间位置的Euler网格,因而在耦合过程中,流体网格需要根据结构边界的移动而变化。特别的,对于超大展弦比构型的低速临近空间飞行器而言,在飞行过程中其结构变形非常显著,因而需要发展适用于大变形的动网格策略。
目前,动网格主要的实现方法可分为两大类[7]:网格重构和网格变形。网格重构技术基于超限插值(TransFinite Interpolation,TFI)技术,在每次边界变化时,重新划分网格,这种方法计算量较大,效率较低。另一种常用的动网格方式是网格变形技术,该方法将网格作为弹簧或弹性体来处理,并根据静力平衡计算得到新的网格点位置。但是弹簧算法在处理大变形或者较密的网格时,常会出现交叉而产生负体积网格,导致网格更新失败。近年来, Liu[7]等采用Delaunay背景网格的变形方法实现网格更新,这种动网格方法能够适应于大变形的情形,特别是对于大的位移情况,然而当有大的扭转变形时,将会出现Delaunay图的交叉,而导致网格更新失败。
本文提出一种基于映射的网格变形策略,其基本思想是:不改变网格的拓扑结构,将边界的变形量按照一定的权重映射到流域中的网格点,从而确定流场中网格的位移。选取待移动网格节点到边界上点的距离倒数的n次方作为权重,其出发点是,要调整的网格点到边界网格点距离越近,受到边界网格点的影响也越大,通过调整指数n可以调整影响的扩散范围。
1 网格变形
1.1 网格变形方法
网格更新方法可分为四个步骤:
第一步,计算网格节点至边界点的距离。设计算域为D,节点个数为p,边界区域为B,节点个数为q,其中D包括B。则计算域D内任意一点i到边界B上一点j的距离为dij。且:
(1)
第二步,计算边界网格点位移量。按照一定的要求变化边界区域B,得到网格边界B上任意一点j的位移量:
(2)
第三步,选取距离的倒数的n次方作为网格更新的权重,计算网格位移量。对于区域D内的任意一点i而言,根据选取的n,按照映射关系,可确定其位移量为:
(3)
有一点需要特别注意的是,当点为边界上的点时,其位移变化则不受到其他点的影响。即若dij=0,则该点的位移为:
Δri=Δrj
(4)
第四步,根据上述位移量,重新确定网格点坐标。对于计算域D内的任意一点i,其新的坐标位置为:
(5)
1.2 网格更新的实现
整个网格变形的思想是:将边界的运动按照某种权重映射到每个网格点上。因而在实现过程中,可分为内外层两个循环,内层是计算边界位移对于某一网格节点的权重,得到网格点位移;外层则是循环所有网格节点,更新坐标位置。
具体过程可写为如下的伪代码:
for i=1:number of domain points
{
Δrsum=0;
dback=0;
for j=1:number of boundary points
{
更新边界点j坐标,得到Δrj;
计算该点到边界点j的距离dij;
if dij= 0
{
Δrsum=Δrj;
dback=1;
break;
}

}
end
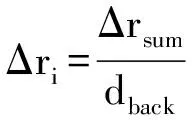
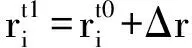
}
end
2 权重指数的影响
选取(1/d)n作为权重,出发点是:要调整的网格点到边界网格点距离越近,受到边界网格点的影响也越大,通过调整指数n可以调整影响的扩散范围。
下面结合二维大变形的动网格算例,通过观察不同的n值得到网格的差异,研究n的取值对于网格变形的影响规律。设原始网格如图2所示,将大变形分为内部物体的扭转变形和平移变形两种情况。则不同的n值对应的变形网格如图3和图4所示。

图2 原始网格Fig.2 The initial mesh
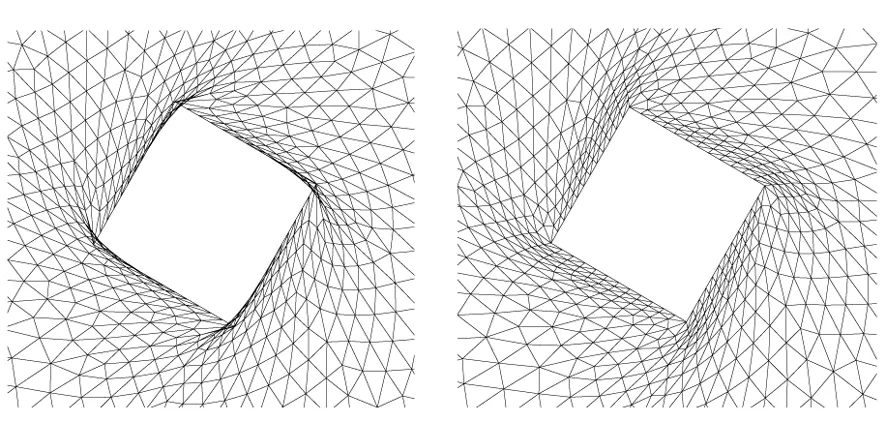
(a)n=2时网格(a) The mesh while n=2(b) n=4时的网格(b) The mesh while n=4
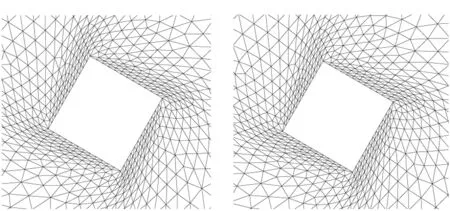
(c) n=6的网格(c) The mesh while n=6(d) n=8的网格(d) The mesh while n=8图3 物体转动时不同n值对应的物体周围网格Fig.3 The mesh versus different n with torsion deformation
对于纯扭转位移而言,假设扭转角度为60°。当n=2时变形网格如图3(a)所示,可以看出,外层网格变形较小,而内层网格扭曲较为严重,出现负体积网格。而随着n值的增大,内层网格对于变形壁面的跟随性也越好,外层网格扭转幅度增大,这也意味着壁面网格质量更好,如图3(c)、(d)。
平移变形情况下,不同的n对应的网格变形结果如图4所示。可以看出,n取值越大,变形物体周围内层网格的变形越小,边界的平移变形被传播到更远的外层网格区域。然而当外层网格需要承受非常大的变形时,则可能会出现交叉而使得网格更新失败。
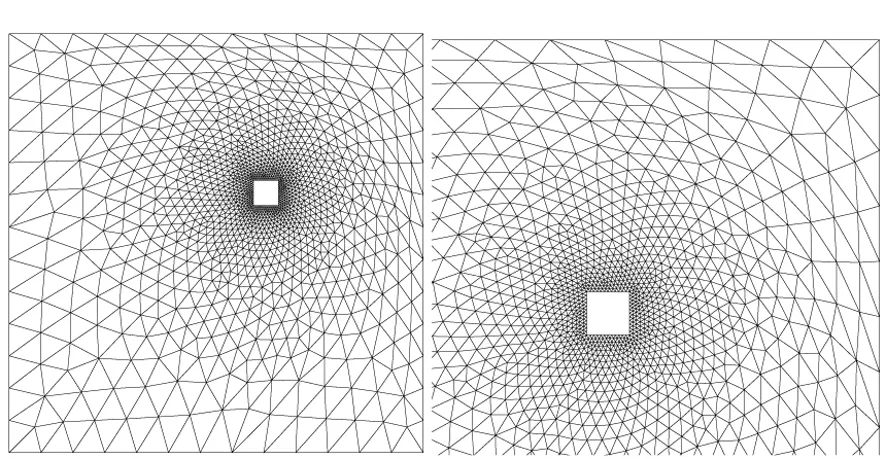
(a) n=2时网格(a) The mesh while n=2

(b) n=3时网格(b) The mesh while n=3
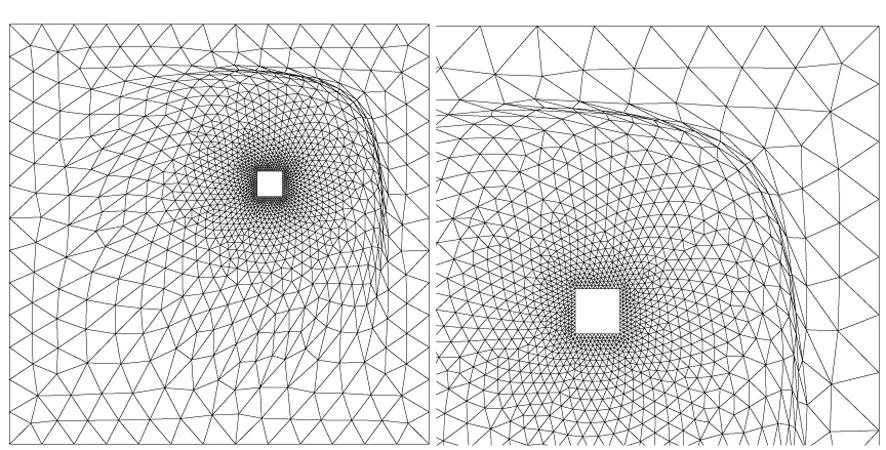
(c) n=4时网格(c) The mesh while n=4图4 物体平移时不同n值对应的物体周围网格 Fig.4 The mesh versus different n with large displacement
通过设定不同的n值,观察网格变形的规律,可以发现:n值越大,运动边界周围网格的刚性越强,对于扭转变形的适应能力也越强;而对于平移变形而言,当n较大时,运动壁面的位移传播到外层网格中,而使得远离壁面的区域的网格变形较大。综上,n值的选取可采取如下的原则:一般n取2~6,且当扭转变形较大时,可取相对较大的n值,而当平移较大时,可适当取较小的n值。同时,对于初始网格本身而言,更大的流域以及较大的外部网格尺寸也会增大网格变形的空间,增强变形能力。
3 网格变形实例
下面结合不同的大变形动网格实例,分析变形后网格的质量。算例包括二维翼型的旋转与平移、二维不规则变形、三维球体的变形与移动以及三维机翼大幅纵向变形。
3.1 二维翼型网格变形
在飞行器的性能分析中,对典型截面的非线性气动弹性研究具有重要的意义。基于计算流体力学的分析手段能够非常好地预测流体的分离等非线性现象等。下面考虑如下的翼型C形结构化网格,如图5所示,当翼型具有大的平移和扭转时,根据上述方法得到的网格分别如图6、图7、图8所示。

图5 翼型原始网格Fig.5 The initial mesh of airfoil

图6 翼型扭转60°网格变形图(n=4)Fig.6 The mesh with 60° torsion deformation (n=4)
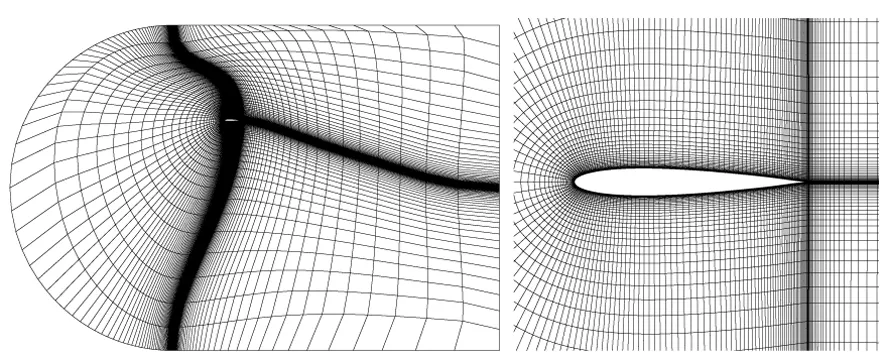
图7 大范围平移后网格变形图(n=2)Fig.7 The mesh with large displacement (n=2)

图8 翼型同时扭转和平移后的变形网格(n=2)Fig.8 The mesh with large displacement and torsion (n=2)
由上述变形后的网格可以看出,在翼型出现非常大的扭转或者平移时,可以通过调节权重指数n的值,将翼型边界的位移很好的传播到大尺寸的网格中,从而保证良好的壁面边界层网格质量。
3.2 二维壁面不规则变形
在飞行器外形设计及翼型优化等方面,可能会涉及到曲线或曲面的不规则变形等情形。针对如图9所示的网格区域,假设内部边界的上表面出现正弦波动变形,而下表面出现锯齿状变形。
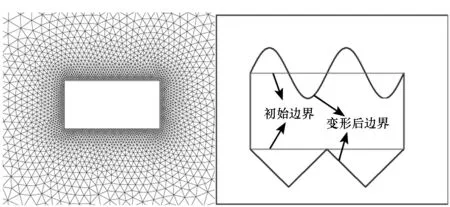
图9 初始网格以及边界变化Fig.9 The initial mesh and the deformation of the wall
观察上述边界变化,可知这种变形主要是小区域内的大扭转变形,此时我们需要保证靠近壁面的网格质量,并避免出现过度扭曲而导致网格更新失败,根据上面n值的选择原则,应取较大的n值,以保证壁面附近网格的刚度,此处取n=6,如图10所示为更新后的网格。

图10 更新后的网格(n=6)Fig.10 The mesh after deformation (n=6)
对于上表面而言,边界扭曲较为严重,网格受到一定的拉伸或压缩;而对于下表面而言,网格变形后依然较为均匀;而侧面由于未变形,网格变化很小。可以看出,当壁面出现不规则变形时,采用这种动网格方法,通过选取合适的n值,能够较好地保证变形后的网格质量。
3.3 三维球体网格变形
对于临近空间球形或者艇形的浮空器而言,当内外压差变化或者受到外界气流干扰时,其结构会出现大幅变形。下面以三维球体的外流场计算网格为例,验证上述动网格方法。
球体的原始网格如图11所示,在球体的周围网格较密,而外层网格较为稀疏。图12(a)、(b)、(c)分别为球体发生平移、变形、扭转后的变形网格结果。可以看出,采用上述网格变形方法,能够获得高质量的网格。
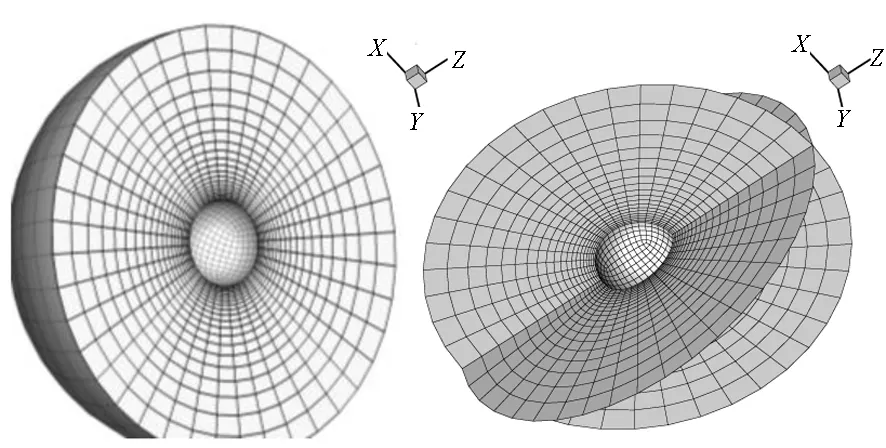
图11 球体原始网格Fig.11 The initial mesh of sphere


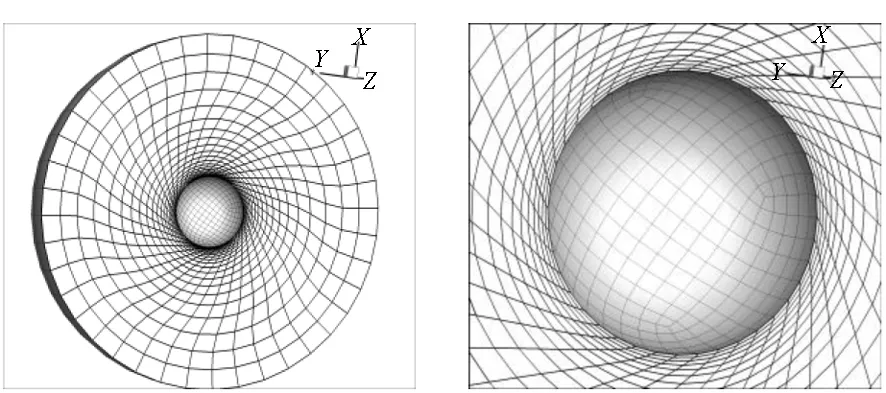
(c) 内部球体旋转60°网格图(n=6)(c) The mesh with 60° rotation of inside sphere (n=6)图12 不同变形情形下的网格结果Fig.12 The mesh with different deformation case
3.4 三维机翼网格变形
对于临近空间大展弦比长航时太阳能飞机而言,为了降低能源消耗,其重量通常相对较小,由此导致结构刚度不足,在飞行过程中常常会出现非常大的纵向变形。下面假定一定幅度的机翼纵向变形,查看上述动网格方法对于变形的适应性及变形后网格的效果。
在机翼的气动力计算中,通常机翼周围的网格较密(以提高计算精度),而远离机翼壁面的区域网格非常稀疏,如图13所示。
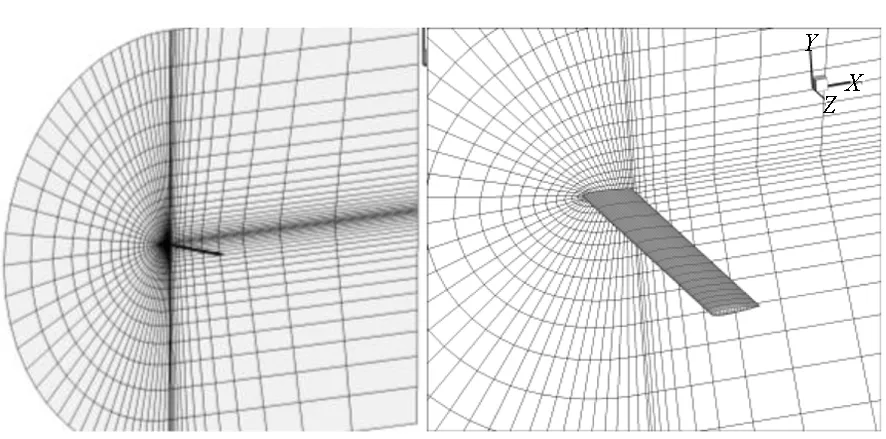
图13 机翼原始网格Fig.13 The initial mesh of wing
希望在网格变形后,依然能够保持良好的壁面网格质量。假设机翼的翼尖纵向变形量达到展长的50%,如图14所示。采用本文的网格变形策略得到变形后的网格如图15、图16所示。可以看出,大的纵向变形出现后,机翼壁面周围网格质量依然较好,而变形被传播到远离机翼壁面的外层大尺度网格中,这对气动计算而言非常重要。

图14 机翼纵向变形Fig.14 The longitudinal deformation of the wing
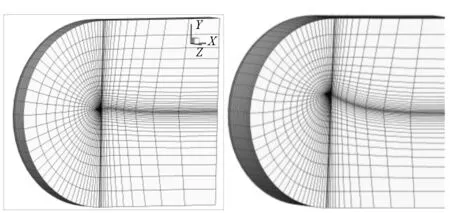
图15 不同截面上的网格(n=4)Fig.15 The mesh at different sections (n=4)

图16 变形后的机翼网格(n=4)Fig16 The wing mesh after deformation (n=4)
4 结论
基于映射的思想,提出一种网格变形策略,其基本思想是:将边界的变形量以某种权重反映到流场区域网格中。文中以(1/d)n为权重,并结合二维算例研究了指数n对于网格变形的影响,结果表明,指数n值越大,边界周围网格的刚性越强,而变形更容易被传播到远离边界的区域。n值的选取可采取如下的原则:一般取2~6,当扭转变形较大时,可取相对较大的n值,而当平移较大时,可适当取较小的n值。
References)
[1]NollTE,BrownJM,Perez-DavisME,etal.Investigationoftheheliosprototypeaircraftmishap,volumeI:mishapreport[R].USA:NationalOceanicandAtmosphericAdministration, 2004.
[2]YangGW,ChenDW,CuiK.Responsesurfacetechniqueforstaticaeroelasticoptimizationonahigh-aspect-ratiowing[J].JournalofAircraft, 2009, 46(4): 1444-1450.
[3]PalaciosR,CesnikCES.Staticnonlinearaeroelasticityofflexibleslenderwingsincompressibleflow[C]//Proceedingsof46thAIAA/ASME/ASCE/AHS/ASCStructures,StructuralDynamicsandMaterialsConference, 2005.
[4]HallissyBP,CesnikCES.High-fidelityaeroelasticanalysisofveryflexibleaircraft[C]//Proceedingsof52ndAIAA/ASME/ASCE/AHS/ASCStructures,StructuralDynamicsandMaterialsConference, 2011.
[5]GarciaJA.Numericalinvestigationofnonlinearaeroelasticeffectsonflexiblehigh-aspect-ratiowings[J].JournalofAircraft, 2005, 42(4): 1025-1036.
[6]CarnieG,QinN.Fluid-structureinteractionofHALEwingconfigurationwithanefficientmovinggridmethod[C]//Proceedingsof46thAIAAAerospaceSciencesMeetingandExhibit, 2008.
[7]LiuXQ,QinN,XiaH.FastdynamicgriddeformationbasedonDelaunaygraphmapping[J].JournalofComputationalPhysics, 2006, 211(2): 405-423.
Moving mesh strategy for large deformation of near-space aircrafts
LIU Zhaowei, HOU Zhongxi,CHEN Lili
The high-aspect-ratio low-speed near-space aircrafts may undergo very large deformation during flight, so a high demand of moving mesh is required for the analysis method based on computational fluid dynamics. To this end, a moving mesh strategy for large deformation of the boundary was presented. The strategy which is based on the mapping interpolation method reflects the displacement of boundary mesh to flow field mesh using a certain kind of weight and then updates the position of mesh nodes. Inverse distance’snth-power was chosen as the weighting factor and the influence of different weight indexnon the mesh deformation was studied, then the analysis of some two-dimensional and three-dimensional moving mesh cases was carried out. The results suggest that this method is capable of handling the large deformation and ensuring the quality of deformed mesh.
moving mesh; large deformation; deformation strategy
2015-04-08
国家高分重大专项资助项目(GFZX04060103)
柳兆伟(1988—),男,安徽临泉人,博士研究生,E-mail:liuzhaowei@nudt.edu.cn;侯中喜(通信作者),男,教授,博士,博士生导师,E-mail:hzx@nudt.edu.cn
10.11887/j.cn.201504004
http://journal.nudt.edu.cn
V211.3
A
1001-2486(2015)04-019-06

