动态滑翔动力学建模与风梯度能量获取*
单上求,侯中喜,朱炳杰,高显忠
动态滑翔动力学建模与风梯度能量获取*
单上求,侯中喜,朱炳杰,高显忠
(国防科技大学 航天科学与工程学院, 湖南 长沙 410073)
为简化问题描述和便于数学操作,对无动力飞机的动态滑翔问题做了假设,并在这些假设下建立了无动力飞机动态滑翔的动力学模型,即三维速度空间中只有一个输入变量的常微分方程组。之后,从理论上得到了这个三维速度空间中机械能可以增加的最大范围,即能增纺锤体内部,并推导出最大的机械能增加率。得出更大的风梯度、更小的阻力系数和更小的面质比更加有利于飞机获取能量的结论,该结论加深了对动态滑翔能量观点的认识,对实践有指导意义。
动态滑翔;风梯度能量获取;无动力滑翔
(CollegeofAerospaceSciencesandEngineering,NationalUniversityofDefenseTechnology,Changsha410073,China)
不难证明无动力飞机飞行在平静的空气中即便做出任何机动都会最终飘落到地面。但人们观察到在自然界中的一些鸟类如信天翁能够飞行很长时间而不扑打翅膀[1]。信天翁可以在一次猎食飞行中飞行长达3 600~15 000km[2]。在如此长距离的飞行中如果时刻保持扑打翅膀信天翁会耗尽体能。假如人造飞行器能够像信天翁一样飞行,那么航时和航程将会显著扩展,或是节省大量的能源。如果临近空间长航时飞行器能够使用这项技术是非常有前途的。那些鸟类之所以能够飞这么久是由于环境中的上升气流或非均匀风场。陆地鸟类倾向利用上升气流(静态滑翔),而海洋鸟类主要利用风梯度(动态滑翔)[1]。后者正是单上求等的研究焦点。
Rayleigh勋爵或许是探索动态滑翔物理秘密的第一人。他解释了为什么信天翁不可能在水平均匀风场条件下不拍打翅膀飞行。他还给出了后来研究者普遍使用的对于动态滑翔的描述性分析。他展示了穿过两层水平切变风的环形运动的物理观点[3]。简而言之,当信天翁在不同风速的切变风场中飞行时,它总是试图获得额外的空速用以保持飞行高度。
理论上讲只要有陡峭的风梯度就可以进行动态滑翔。实际生活中,这样的情形可能发生在山坡背风侧的分离流中以及地面边界层或阵风里[1]。Idrac的文章指出试验显示随高度增高而加剧的风场总是存在于信天翁飞行的海面上空[4]。圣地亚国家实验室成功地在山坡背风侧进行了遥控动态滑翔试验[5]。Gordon的论文描述了由NASA支持的全尺寸滑翔机有人动态滑翔试验[5]。实际上,大量的遥控滑翔机爱好者经常在山坡背风侧实现动态滑翔,例如每年八月底举行的名为Rosendal山坡周末的滑翔活动[6]。气象气球测量的数据也展示了梯度风场几乎存在于地面以上30km范围内的每一个高度上[7]。这意味着动态滑翔的适用范围很广阔。尽管如此,目前还没有确信证据证实全自主动态滑翔已经成功实现。
另一方面,对于动态滑翔的理论研究在Rayleigh之后仍在继续。Wood把动态滑翔的运动简化为一个二维模型并给出了基于空速的常微分方程,他研究和模拟了在对数风场中的两类完整的飞行循环[8]。Hendriks推导出了三自由度质点动力学方程并且得到了不沉降解的条件[9]。
由于计算机革命,很多以往认为难以进行的计算如今可以在个人计算机上完成。因此,动态滑翔路径规划就成了近年来的热门话题。Boslough的报告使用了遗传算法优化Rayleigh循环[1]。Zhao使用NPSOL软件数值优化了无动力飞机[10]和有动力飞机[11]动态滑翔的最小循环。Sachs导出了动态滑翔的最优控制问题并且给出了数值结果[12],还计算出使用他所提供方法生成轨迹的最小风切变强度[13]。Deittert利用微分平滑特点简化了该最优化问题[14]。高显忠采用了一个简化的分段模型用以优化动态滑翔问题[15]。文献[16]是一篇比较全面地介绍动态滑翔的综述文章,更多细节内容可资借鉴。
1 系统模型
1.1 飞机与风场假设
为了简化问题但不破坏问题的本质,对飞机和风场做出了假设。
对于飞机,假设如下:
1)飞机无动力,即没有推力作用于其上;
2)飞机的转动是瞬间完成的,只需考虑飞机的平移动力学;
3)飞机是自稳定的,即飞机始终指向空速方向;
4)倾侧角是系统唯一的控制输入,可以通过偏转副翼实现,且倾侧角可瞬间到达。
文献[10-12]、[14]和[17]做了和以上第二条同样的假设。第三条和第四条假设意味着飞机没有了改变升阻比的能力,只有一个倾侧角控制输入让系统更加清晰,在数学上更易操作。根据第三条假设,由于飞机始终是零攻角,因此飞机的升力系数和阻力系数近似不变[18]。第三条和第四条假设同文献[13]所做的假设一致。
另一方面,对于风场该假设只有随着高度呈均匀线性变化的单向水平切变风。如图1所示,风速的改变正比于高度差,这意味着风梯度是飞机所在局部区域的斜率。这里假设的风场实际是全局风场的局部近似。该风场假设同文献[10]和[11]中的假设相同。
1.2 坐标系
坐标系的定义如图1所示。O-xyz是一个非惯性系,原点O在水平面内同飞机所在高度的风一起运动,即与飞机所在当地的风具有相同的速度。z轴竖直向上指向天空。对于x轴,如果风速随着高度增大,x轴就指向风速的反方向;如果风速随着高度减小,则x轴指向风的方向。y轴由右手定则决定。在图1中,惯性系O0-x0y0z0与非惯性O-xyz在初始时刻重合且永远固连在地面上。

图1 坐标系和风场Fig.1 Coordinates and wind field
1.3 动力学方程
根据1.1节中的四条假设,三维的质点动力学方程足以描述这个问题。由于O-xyz坐标系相对于惯性坐标系没有旋转运动,因此飞机所受的力只有气动力、重力和牵连惯性力[19],如图2所示。
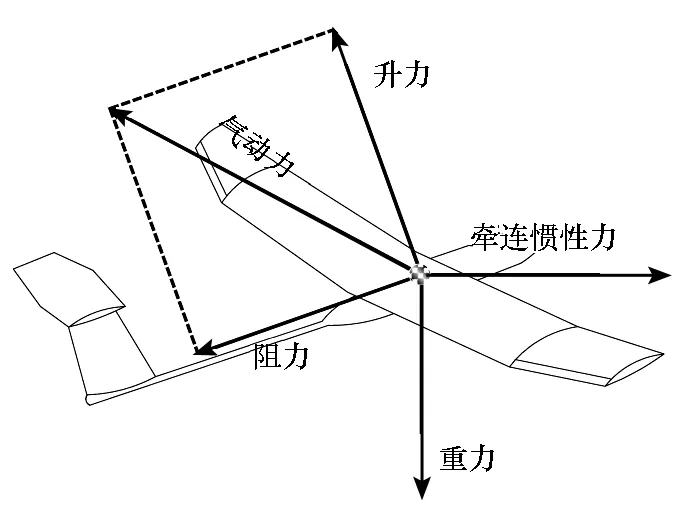
图2 作用在飞机上的力Fig.2 Forces acting upon the aircraft
由于参考系随风移动,牵连惯性力Fi可以表示为
(1)
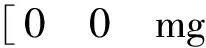
(2)
(3)
其中:ρ是空气密度;v是速度大小,数值上等于空速;s是翼面积[18]。CL和CD分别是升力系数和阻力系数,且满足以下关系:
(4)
其中L/D是升阻比。为了使用方便,定义
(5)
(6)
升力和阻力在O-xyz坐标系里可以表示成
(7)
(8)
其中,vx,vy和vz是速度的三个坐标分量,v是速度的大小,而φ是倾侧角。那么,动力学方程可以根据牛顿定律[19]给出
(9)
将PLm=PL/m和PDm=PD/m代入式(9),最终得到
(10)
其中,vx,vy和vz是系统状态,而φ是唯一的系统输入。后面关于机械能增加率的讨论也将在这个三维速度空间中讨论。
2 机械能增加率
令E代表非惯性系O-xyz中的机械能,根据动能定理[19],则机械能的变化等于阻力和惯性力做功,因为升力始终垂直于运动方向,故其不做功。因此可得
dE=-Ddl+mGwvzdx
(11)
其中dl为线元,可以表示为
dl=vdt
(12)
将式(12)代入式(11)得到
(13)
所以,单位质量的机械能增加率
(14)
由式(14) 可见,机械能的瞬时改变不受控制输入倾侧角φ的影响,只是速度空间中的系统瞬时位置的函数,倾侧角φ在该时刻只影响系统下一刻的走向。令式(14)右侧为函数
(15)
直角坐标系中的速度可以按式(16)转换为球坐标:
(16)
其中,r是径向速度,θ是俯仰角,ψ是偏航角。便于画图,将式(16)代入式(15),可得其球坐标形式
(17)
若PDm等于0.003,Gw等于1.2,本文所有单位都是采用国际单位制,因此量纲符号都予以省略。图3为函数(17)的等值面图,同一等值面上的点具有相同的d(E/m)/dt,即等值面为等机械能增加率面。

图3 函数f等值面图(上半叶为半剖图)Fig.3 Contour graph of function f(the upper half is semi-sectional view)
2.1 能增纺锤体
机械能增加率为0的等值面方程为
(18)
其恰好将速度空间分割为机械能增加率为正(面内部机械能增加)与机械能增加率为负(面外部机械能减小)的两部分。因此称其所包裹的体为能增纺锤体(如图3所示的曲面所包裹的体)。从式(18)还可以看出,Gw/PDm的比值越大,能增纺锤体的体积越大,直观上讲,系统增加机械能的可能性越大。因此,增加风梯度Gw、减小阻力系数CD和减小面质比s/m有利于能量获取。同时由式(18)可见,能增纺锤体位于vx>0,vz>0或vx<0,vz<0的四个卦限内。而系统只有在能增纺锤体内才可能增加机械能,这印证了文献[3]中正风梯度(风速随高度增高而增大)下信天翁逆风上升(对应vx>0,vz>0),顺风下降(vx<0,vz<0)可获得能量的结论。
2.2 最大机械能增加率
(19)
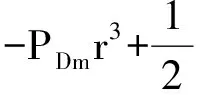
(20)
转换为直角坐标对应于
(21)
其最大值为
(22)
这就是最大的机械能增加率,由式(22)可见,若想增加单位质量的最大机械能增加率,可以增加风梯度Gw、减小阻力系数CD和减小面质比s/m。该结论和2.1节的结论相一致。
3 结论
直观上看,无动力飞机在切变风场中能够持续飞行在于其能量得到了补充。本文对于能量获取问题,从理论上给出了比Rayleigh更加准确的结论,即只有在能增纺锤体内部才可能获取额外的能量,而机械能增加的速率也有其极限值,并不是无限制的。更大的风梯度Gw、更小的阻力系数CD和更小的面质比s/m有利于飞机获取额外的机械能。
References)
[1]BosloughMBE.Autonomousdynamicsoaringplatformfordistributedmobilesensorarrays[R].SandiaNationalLaboratories,SandiaNationalLaboratories,SAND2002-1896, 2002.
[2]JouventinP,WeimerskirchH.Satellitetrackingofwanderingalbatrosses[J].Nature,1990, 343(22): 746-748.
[3]RayleighJWS.Thesoaringofbirds[J].Nature,1883, 27(701): 534-535.
[4]IdracP.Experimentalstudyofthe"soaring"ofalbatrosses[J].Nature, 1925, 115(2893): 532.
[5]GordonRJ.Optimaldynamicsoaringforfullsizesailplanes[D].USA:AirUniversity, 2006.
[6]JohnG.Rosendalslopeweekend2006[Z].SoaringDigest,2006, 23:10, 40-43.
[7]ZhuB,HouZ,ChenQ,etal.TheoreticalandexperimentalresearchofUAV′senergyvariationindynamicsoaring[J].JournalofCentralSouthUniversity, 2014.
[8]WoodCJ.Theflightofalbatrosses(acomputersimulation)[J].Ibis, 1973, 115(2): 244-256.
[9]HendriksF.Dynamicsoaringinshearflow[C]//Proceedingsof2ndInternationalSymposiumontheTechnologyandScienceofLowSpeedandMotorlessFlight,AIAA74-1003, 1974.
[10]ZhaoYJ.Optimalpatternsofgliderdynamicsoaring[J].OptimalControlApplicationsandMethods, 2004, 25(2): 67-89.
[11]ZhaoYJ,QiYC.Minimumfuelpowereddynamicsoaringofunmannedaerialvehiclesutilizingwindgradients[J].OptimalControlApplicationsandMethods, 2004, 25(5): 211-233.
[12]SachsG,BussottiP.Applicationofoptimalcontroltheorytodynamicsoaringofseabirds[J].VariationalAnalysisandApplications, 2005, 79: 975-994.
[13]SachsG.Minimumshearwindstrengthrequiredfordynamicsoaringofalbatrosses[J].Ibis, 2005, 147(1): 1-10.
[14]DeittertM,RichardsA,ToomerCA,etal.Enginelessunmannedaerialvehiclepropulsionbydynamicsoaring[J].JournalofGuidance,Control,andDynamics, 2009, 32(5): 1446-1457.
[15]GaoXZ,HouZX,GuoZ,etal.Analysisanddesignofguidance-strategyfordynamicsoaringwithUAVs[J].ControlEngineeringPractice, 2014, 32: 218-226.
[16]GaoXZ,HouZX,GuoZ,etal.Energyextractionfromwindshear:reviewsofdynamicsoaring[J/OL]//ProceedingsoftheInstitutionofMechanicalEngineers,PartG:JournalofAerospaceEngineering, [2015-02-17].
[17] 朱炳杰,侯中喜. 无人机风梯度滑翔过程中能量变化[J]. 国防科技大学学报,2015, 37(1): 78-83.
ZHUBingjie,HOUZhongxi.Energytransformationindynamicsoaringofunmannedaerialvehicles[J].JournalofNationalUniversityofDefenseTechnology, 2015, 37(1): 78-83.(inChinese)
[18]StevensBL,LewisFL.Aircraftcontrolandsimulation[M].USA:JohnWiley&Sons, 2003.
[19]ArnoldVI.Mathematicalmethodsofclassicalmechanics[M].USA:SpringerScience&BusinessMedia, 1989.
Dynamics modeling of dynamic soaring and energy gaining from the wind gradient
SHAN Shangqiu, HOU Zhongxi, ZHU Bingjie, GAO Xianzhong
Inordertosimplifythedescriptionoftheproblemsandtobeconvenientformathematicalmanipulation,aseriesofhypothesesaboutthedynamicglideproblemofunpoweredaircraftweremade.Underthesehypotheses,adynamicsmodelofdynamicsoaring,whichisa3-dimentionalordinarydifferentialequationsinthevelocityspacewithasingleinput,wasbuilt.Thelargestgrowingareaofmechanicalenergyinthisvelocityspace,whichiscalledenergy-gainedspindle,wasobtainedtheoreticallyandthemaximumrateofenergyincreasingwasalsodeduced.Theconclusionthatthelargerwindgradient,thesmallerdragandthesmallerarea-massratioaremoreinfavorofgainingenergyfortheenginesaircraftgivesadeeperunderstandingofthedynamicsoaringenergyanditcanhelpthepractice.
dynamicsoaring;windgradientenergygaining;unpoweredsoaring
2014-04-10
国家863计划资助项目(2014AA7054035)
单上求(1987—),男,辽宁锦州人,博士研究生,E-mail:ssq870424@126.com;侯中喜(通信作者),男,教授,博士,博士生导师,E-mail:hzx@sina.com
10.11887/j.cn.201504008
http://journal.nudt.edu.cn
V
A

