Co-splitting of Simple Lie Algebras of Type A，D，E

Zhao Yu-e

（School of Mathematics，Qingdao University，Qingdao，Shandong，266071）

Communicated by Du Xian-kun

Co-splitting of Simple Lie Algebras of Type A，D，E

Zhao Yu-e

（School of Mathematics，Qingdao University，Qingdao，Shandong，266071）

Communicated by Du Xian-kun

In this paper，through a meticulous description of finite root system，a concrete comultiplication with an explicit action on the basis elements of finite dimensional simple Lie algebras of type A，D，E is constructed.Then any finite dimensional simple Lie algebra of type A，D，E is endowed with a new generalized Lie coalgebra splitting.This construction verifies the known existence of a co-split Lie structure on any finite dimensional complex simple Lie algebra.

Lie coalgebra，co-splitting，finite-dimensional simple Lie algebra

2010 MR subject classification：17B62，17B05

Document code：A

Article ID：1674-5647（2015）03-0229-13

1　Introduction

During the past decade，a great number of papers study Lie bialgebras.It is well-known that a Lie bialgebra is a vector space endowed simultaneously with a Lie algebra structure and a Lie coalgebra structure，together with a certain compatibility condition，which was suggested by a study of Hamiltonian mechanics and Poisson Lie groups（see［1］）.

Recently，Xia and Hu［2］introduced a new concept“co-split Lie algebra”which is a new［Lie algebra］-［Lie coalgebra］structure，and proved that any finite dimensional complex simple Lie algebra L can be endowed with a co-split Lie structure，i.e.，a co-splitting Lie coalgebra structure such that the composition［·，·］◦δ of the two structure maps δ：L→L⊗CL and［·，·］：L⊗CL→ L coincides with the identity.Using the concept“co-split Lie algebra”，the Lie algebra structure on the dual space of a semi-simple Lie algebra can be easily studied from another point of view.Moreover，Farnsteiner［3］elicited the conceptual sources of［2］，starting from the observation that the coalgebra maps defined in［2］are infact homomorphisms of L-modules，and for Lie algebras affording non-degenerate symmetric associative forms，such coalgebra maps naturally arise by dualizing the Lie multiplication，also several equivalent characterizations of co-splitting of a Lie algebra are given.For the cosplit Lie algebra L of type Al，Xia and Hu［2］have shown an explicit action of the coalgebra map δ on the basis elements of L.For the co-split Lie algebra L of another type，δ is obtained via embedding L→sln（C）and the action of δ on the basis elements of L is not explicitly shown，and may be complicated.In this paper，a co-split Lie algebra structure is given，which generalizes the construction in Theorem 4.2 in［2］，on any complex simple Lie algebra L of type Al（l≥1），Dl（l≥4）or Ek（k=6，7，8），and the coalgebra map δ has an explicit action on the basis elements of L.See Theorem 4.1 in this paper for details.

2　Basic Definitions and Notations

A Lie algebra is a pair（L，［·，·］），where L is a linear space and［·，·］：L⊗CL→L is a bilinear map（in fact，it is a linear map from L⊗CL to L）satisfying

（L1）［a，b］+［b，a］=0；

（L2）［a，［b，c］+［b，［c，a］+［c，［a，b］=0.

For any spaces U，V，W，define linear maps τ：U⊗CV→V⊗CU by τ（u⊗v）=v⊗u，and ξ：U⊗CV⊗CW→V⊗CW⊗CU by ξ（u⊗v⊗w）=v⊗w⊗u.A Lie coalgebra is a pair（L，δ），where L is a linear space and δ：L→L⊗CL is a linear map satisfying

（Lc1）（1+τ）◦δ=0；

（Lc2）（1+ξ+ξ2）◦（1⊗δ）◦δ=0.

A Lie bialgebra is a triple（L，［·，·］，δ）such that

（Lb1）（L，［·，·］）is a Lie algebra；

（Lb2）（L，δ）is a Lie coalgebra；

（Lb3）For any x，y∈L，δ（［x，y］）=x·δ（y）-y·δ（x）.

The compatibility condition（Lb3）shows that δ is a derivation map.In this case，［·，·］◦δ is a derivation of L.Xia and Hu［2］replaced the above（Lb3）with the condition［·，·］◦δ=idLand give the following new concept“co-split Lie algebra”.

Definition 2.1Suppose that（L，［·，·］）is a Lie algebra and（L，δ）is a Lie coalgebra. A triple（L，［·，·］，δ）is called a co-split Lie algebra if［·，·］◦δ=idL.

3　Several Properties of Simple Lie Algebras of Type A，D，E

Let Q be the root lattice of type Al，Dl，or El，and let（·|·）be the bilinear symmetric form on Q such that the root system Φ=｛α∈Q|（α|α）=2｝.Let ε：Q×Q→｛±1｝be an asymmetry function satisfying the bimultiplicativity condition

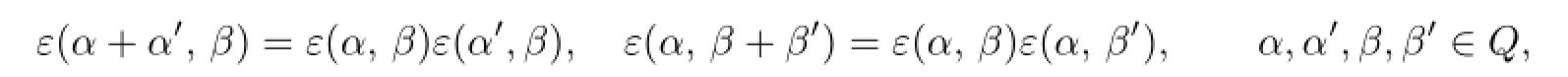
and the condition

An asymmetry function ε can be constructed as follows：choose an orientation of the Dynkin diagram，and let

Define a bracket on L as follows：

By Proposition 7.8 in［4］，L is the simple Lie algebra of type Al，Dl，or El.Denote Π =｛α1，α2，···，αl｝by a simple root system of Φ.For any i=1，2，···，l，there is a fundamental reflection rαion Φ defined by rαi（β）=β-（β|αi）αifor any β∈Φ.

Lemma 3.1If α，β∈Q，and（α|β）=±1，then

（1）ε（α，β）=-ε（β，α）；

（2）ε（β，α-β）ε（α，-β）=1，and ε（β，α-β）ε（-β，α）=-1；

（3）ε（β，α-β）=ε（-α，β）=ε（α-β，-α）.

（2）Let g denote the dual Coxeter number of the simple root system Φ.Then

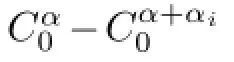
Lemma 3.2For any α∈Φ，the following statements hold：

（1）If α1∈P1α，then α，-α1∈，α，α1-α∈，and-α，-α1+α∈

（2）Define Υα=｛（α1，α2）|α1∈，α2∈-｛α，-α1｝｝.If（β，γ）∈Υα，then（β，α-β-γ）∈Υα.Moreover，either（γ，α-β-γ），（γ，β）∈Υα，or（α-β-γ，β），（α-β-γ，γ）∈Υα；

（3）Define Ξα=｛（α1，α2）|α1∈，α2∈-｛-α，α-α1｝｝，=｛（α1，α2）| α1∈，α2∈-｛α，α1-α｝｝.If（β，γ）∈Ξα，then（β，-γ）∈.Moreover，either（β+γ，-β）∈Ξα，（β+γ，β）∈，or（-γ，β+γ）∈Ξα，（-γ，-β-γ）∈

Proof.（1）By easy calculation，we omit the details.

（2）If（β，γ）∈Υα，then（α|β）=（γ|α-β）=1，and γ/=α，-β.Since（α-β-γ| α-β）=1，then α-β-γ∈.Assume that α-β-γ=α（resp.，-β）.Then γ=-β（resp.，γ=α），a contradiction.Thus（β，α-β-γ）∈Υα.

Next we consider（α|γ）.At first，γ/=α implies that（α|γ）/=2.Assume that（α|γ）=-2（resp.，-1）.Then（γ|β）=（γ|α）-（γ|α-β）=-3（resp.，-2），a contradiction.So（α|γ）/=-2 or-1.Therefore（α|γ）must be equal to 1 or 0.We prove（2）in the following two cases：

5.加强深港金融业的合作。随着CEPA的深入实施，内陆与港澳地区的联系不断加强，尤其是深港两地通关能力不断提高，深港金融一体化趋势越来越明显。深圳可以借助毗邻香港的地理优势，发展成为香港国际金融中心在内陆的延伸。因此，深圳应积极加快金融创新力度，加强深港金融业合作，尽快与香港金融业对接，在为双方的贸易活动提供各项金融服务的同时，合作关系范围也应积极拓展到保险、外汇、证券等各个方面，进一步衔接深港两地的金融市场，促使深港金融最终实现一体化，多渠道、多方面、多层次展开深港金融服务业合作，从而与香港共建“深港国际金融中心”。

Case 1.（α|γ）=1.

Case 2.（α|γ）=0.

In this case，（α-β-γ|α）=1，so α-β-γ∈By calculation，（γ|β+γ）=1. Thus γ∈，i.e.，γ∈Since（α|γ）=0，then γ/= α.Assume that γ=-（α-β-γ）.Then α=β，a contradiction.Thus γ/=-（α-β-γ）.Therefore，（α-β-γ，γ）∈Υα.Moreover，by the preceding proof of（2），（α-β-γ，α-（α-β-γ）-γ）also belongs to Υα，i.e.，（α-β-γ，β）∈Υα.

（3）By condition，（α|β）=（γ|-β）=1，and γ/=-α，α-β.So（-γ|β）=1，i.e.，-γ∈，and-γ/=α，or β-α.Thus（β，-γ）∈

Next we consider（α|γ）.First γ/=-α implies that（α|γ）/=-2.Assume that（α|γ）=2.Then γ=α，and（γ|-β）=（α|-β）=-1，a contradiction.So（α|γ）/=2. Assume that（α|γ）=1.Then（γ|α-β）=2，and so γ=α-β，a contradiction.So（α|γ）/=1.Therefore，（α|γ）must be equal to-1 or 0.We prove（3）in the following two cases：

Case 1.（α|γ）=0.

In this case，（α|β+γ）=1，so β+γ∈.And（-β|-β-γ）=1，so-β∈Since（-α|-β）=1，then-β/=-α.Assume that-β=α-（β+γ）.Then α=γ，acontradiction to that（α|γ）=0.Thus-β∈-｛-α，α-（β+γ）｝.Therefore，（β+γ，-β）∈Ξα，which implies that（β+γ，β）∈by the preceding proof of（3）.

Case 2.（α|γ）=-1.

4　The Main Result

Theorem 4.1Let（L，［·，·］）be a simple Lie algebra of type Al（l≥1），Dl（l≥4），Ek（k=6，7，8）.Define a linear map δ：L→L⊗CL by

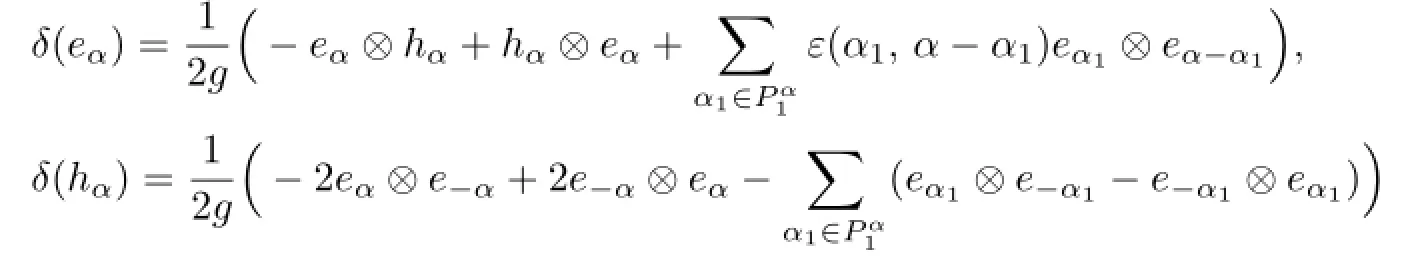
for any α∈Φ，where Pα1is defined in Proposition 3.1（4）.Then the triple（L，［·，·］，δ）is a co-split Lie algebra.

We prove the main theorem via a series of lemmas and propositions.

Proposition 4.1（1+τ）◦δ=0.

Proof.For any α∈Φ，

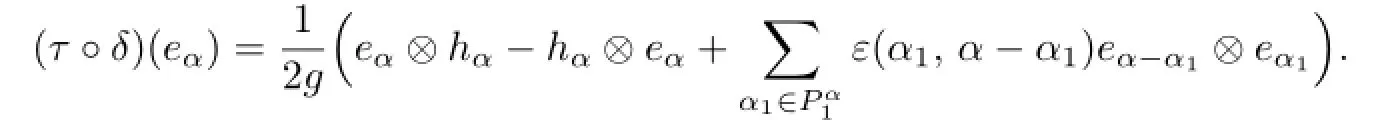
Obviously，α1∈if and only if α-α1∈.Then∑

For α1∈，（α1|α-α1）=-1，then by Lemma 3.1（1），ε（α1，α-α1）=-ε（α-α1，α1）. Thus

and so

It is easy to see that

Thus the proposition holds by the linearity of τ and δ.

Lemma 4.1（（1+ξ+ξ2）◦（1⊗δ）◦δ）（eα）=0 for any α∈Φ.

Proof.For any α∈Φ，

We prove that the action of 1+ξ+ξ2on the above equality is equal to zero by the following three steps（1）-（3）：

（1）By definition of ξ，for any x，y，z∈L，

Similarly，

Thus

（3）Denote

By（1）and（2），we need to prove（1+ξ+ξ2）（R）=0.Denote

where Υαis defined in Lemma 3.2（2）.So

For any α1∈，（α|α1）=1，then by Lemma 3.1（2），

Then

In the above equality（4.1），if（β，γ）∈Υα，then by Lemma 3.3（2），either

or

Set

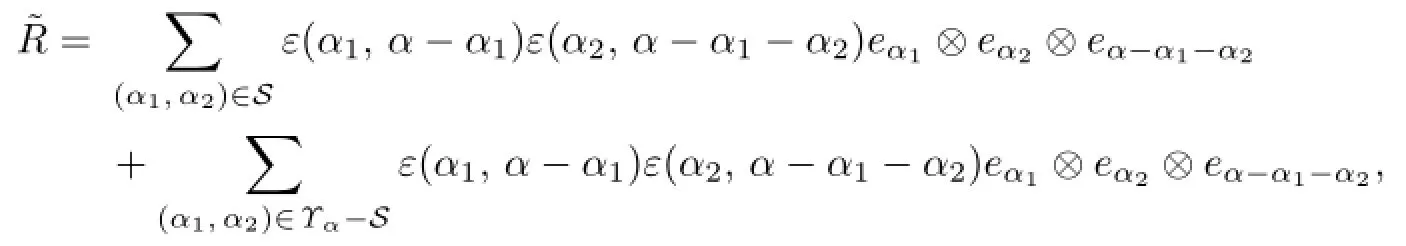
where

or

Next we prove that

in the following two cases：

Case 1.S=｛（β，γ），（β，α-β-γ），（γ，α-β-γ），（γ，β）｝.

In the above equality（4.2），there are four summands respectively corresponding to（β，γ），（β，α-β-γ），（γ，α-β-γ），（γ，β），i.e.，

（i）ε（β，α-β）ε（γ，α-β-γ）eβ⊗eγ⊗eα-β-γ；

（ii）ε（β，α-β）ε（α-β-γ，γ）eβ⊗eα-β-γ⊗eγ；

（iii）ε（γ，α-γ）ε（α-β-γ，β）eγ⊗eα-β-γ⊗eβ；

（iv）ε（γ，α-γ）ε（β，α-β-γ）eγ⊗eβ⊗eα-β-γ.

By calculation，

then

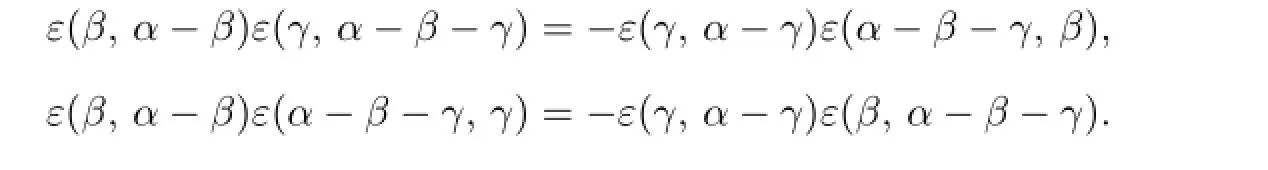
Thus

Case 2.S=｛（β，γ），（β，α-β-γ），（α-β-γ，β），（α-β-γ，γ）｝.

In the above equality（4.2），there are the following four summands：

By calculation，

then

Thus

Since Υαis a finite set，we have

Lemma 4.2（（1+ξ+ξ2）◦（1⊗δ）◦δ）（hα）=0 for any α∈Φ.

Proof.For any α∈Φ，

By definition of ξ，

Denote

Then

We only need to prove that（1+ξ+ξ2）（R′）=0.For convenience，we denote

where Ξα，are defined in Lemma 3.2（3），and denote

By calculation，ε（-α，α1）=ε（α-α1，-α）=ε（α1，α-α1），then

Similarly，

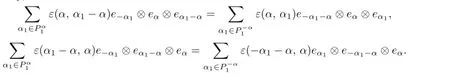
By computation，ε（α，α1）=ε（-α1-α，α）=ε（α1，-α-α1），then

So it remains to show that（1+ξ+ξ2）（˜R′）=0.

If（β，γ）∈Ξα，then by Lemma 3.2（3），either

or

So

where either

or

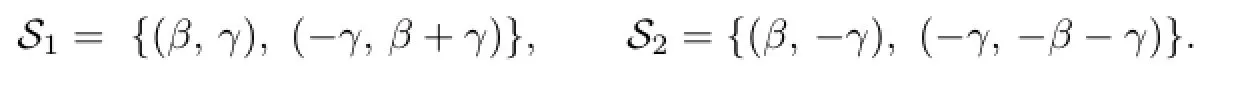
Next we prove that

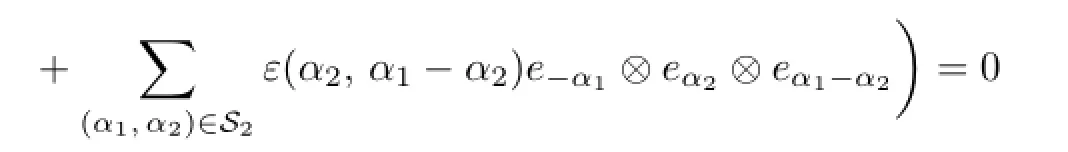
in the following two cases：

Case 1.S1=｛（β，γ），（β+γ，-β）｝，and S2=｛（β，-γ），（β+γ，β）｝.

In this case，ε（γ，-β-γ）=ε（β，γ），ε（-β，-γ）=ε（-γ，β+γ）.Therefore，

Case 2.S1=｛（β，γ），（-γ，β+γ）｝，and S2=｛（β，-γ），（-γ，-β-γ）｝.

It is easy to see that ε（γ，-β-γ）=ε（-β-γ，β），ε（-γ，β+γ）=ε（β+γ，-β）.Thus

Therefore

by induction.

Proof of Theorem 4.1By Lemmas 4.1，4.2 and Proposition 4.1，（L，δ）is a Lie coalgebra.

For any α∈Φ，

By Lemma 3.2（3），（［·，·］◦δ）（eα）=eα.And

By Proposition 3.1（4），

So

Therefore，（L，［·，·］，δ）is a co-split Lie algebra.

Remark 4.1We give an example to explain that the construction in Section 4 in［2］is a special case of our construction.Suppose that L is a complex simple Lie algebra of type Al，l≥1.It can be realized as the special linear Lie algebra sll+1（C）with basis｛Ei，j，-Ej，i，Ei，i-Ej，j|1≤i＜j≤l+1｝.Set η be the set spanned by the basis elements｛Ei，i-Ej，j|1≤i＜j≤l+1｝.Then η is a Cartan subalgebra of L.Correspondingly，

We choose a fixed Chevalley basis as follows：

Then the action of the comultiplication δ on eα，e-α，hαunder our definition in Theorem 4.1 is exactly that in Theorem 4.2 in［2］.

References

［1］Etingof P，Schiffmann O.Lectures on Quantum Groups.Boston：Internat.Press，1998.

［2］Xia L，Hu N.Introduction to co-split Lie algebras.Algebra Represent.Theory，2011，14：191-199.

［3］Farnsteiner R.Lie algebras with a coalgebra splitting.Algebra Represent.Theory，2011，14：87-96.

［4］Kac V G.Infinite Dimensional Lie Algebras（third edition）.Combridge：Cambridge Univ.Press，1990.

［5］Suter R.Coxeter and dual coxeter number.Comm.Algebra，1999，26：147-153.

10.13447/j.1674-5647.2015.03.05

date：Sept.8，2013.

The Anhui Province College Excellent Young Talents Fund（2013SQRL071ZD）.

E-mail address：blueskyyu2004@aliyun.com（Zhao Y E）.