Globals of Completely Regular Monoids

Wu Qian-qian anD Gan Ai-ping

（College of Mathematics and Information Science，Jiangxi Normal University，Nanchang，330022）

Communicated by Du Xian-kun

Globals of Completely Regular Monoids

Wu Qian-qian anD Gan Ai-ping*

（College of Mathematics and Information Science，Jiangxi Normal University，Nanchang，330022）

Communicated by Du Xian-kun

An element of a semigroup S is called irreducible if it cannot be expressed as a product of two elements in S both distinct from itself.In this paper we show that the class C of all completely regular monoids with irreducible identity elements satisfies the strong isomorphism property and so it is globally determined.

completely regular monoid，irreducible element，power semigorup

2010 MR subject classification：06A12

Document code：A

Article ID：1674-5647（2015）03-0222-07

1　Introduction and Preliminaries

The power semigroup，or global，of a semigroup S is the semigroup P（S）of all nonempty subsets of S equipped with the multiplication

A class K of semigroups is said to be globally determined if any two members of K having isomorphic globals must themselves be isomorphic.

Tamura［1］asked in 1967 whether the class of all semigroups is globally determined.The question was negatively answered in the class of all semigroups by Mogiljanskaja［2］in 1973. Crvenkovi´c et al.［3］proved that involution semigroups are not globally determined in 2001. But it is known that the following classes are globally determined：groups［4-5］；rectangular groups［6］；completely 0-simple semigroups［7］；finite semigroups［8］；lattices and semilattices［9-10］，finite simple semigroups and semilattices of torsion groups in which semilattices are finite［11］；completely regular periodic monoids with irreducible identity［12］.

In this paper we devote to the study of the global determinacy of completely regular semigroup and show that the class of all completely regular monoids with irreducible identityelement satisfies the strong isomorphism property and so it is globally determined.Recall that a class K of semigroups is said to satisfy the strong isomorphism property if for any S，∈K and for every isomorphism ψ from P（S）to（the restriction of ψ to S）is an isomorphism from S to，where S（resp.S′）is considered to be a subset of P（S）（resp.by identifying an element x of S（resp.S′）with the singleton set｛x｝.It was proved by Kobayashi［10］that the class of semilattices satisfies the strong isomorphism property.

A few words on notation and terminology are in order.The set of idempotents of a semigroup S is denoted by E（S），and for each a∈S the H-class of S containing a is denoted by Ha（S）.A singleton member of P（S）frequently is identified with the element it contains.An element a∈S is termed irreducible if it cannot be expressed as a product of two elements in S both distinct from themselves，i.e.，if there exist b，c∈S such that a=bc，then a=b or a=c.It is clear that if S is a monoid whose identity element 1 is irreducible，then 1=bc implies that 1=b=c.

We refer to the books［13-16］for all background information concerning semigroups and universal algebra.

2　Main Results

In this section，we denote the class of all completely regular monoids with irreducible identity elements by C.For convenience，for every monoid S，we use 1 rather than 1Sto denote its identity element.

Our main result，establishing the global determinacy of C，is proved via a sequence of lemmas.The first lemma implies that the class of all groups is globally determined，which is taken from Gould and Iskra［11-12］.

Lemma 2.1［11］Let S be a semigroup and e∈E（S）.Then He（P（S））=He（S）.

Lemma 2.2Let S∈C，and let A be an idempotent in P（S）.Then|A|＞1 if and only if A satisfies one of the following two statements：

（i）A=｛1，a｝B or A=B｛1，a｝for some B∈P（S）｛A｝and some a∈A；

（ii）A=C2for some C∈P（S）such that C/=C3.

Proof.It follows immediately from Lemma 2.2 in［12］.

Lemma 2.3［12］Let S∈C.For A∈P（S）the following statements are equivalent：

（i）There exists an e∈E（S）such that A=｛1，e｝；

（ii）A is idempotent and irreducible，and the only solutions to XA=A are｛1｝and A.

Lemma 2.4Let S∈C，and A∈P（S）.Then there exist a∈SE（S）and a2∈E（S）such that A=｛1，a｝if and only if A satisfies the following statements：

（i）A2is idempotent，and A is not idempotent；

（ii）There is a unique e∈E（S）｛1｝such that A2｛1，e｝=A2；

（iii）A｛1，e｝=A2，where e is given as in（ii）；

（iv）If A2=UV for some U，V∈P（S）satisfying U/=｛1｝and V/=｛1｝，then one of the following cases holds：

（1）U=V=A；

（2）U=A，V=｛1，e｝；

（3）U=A，V=A2；

（4）U=｛1，e｝，V=A；

（5）U=｛1，e｝，V=A2；

（6）U=A2，V=｛1，e｝；

（7）U=A2，V=A；

（8）U=V=A2，

where e is given as in（ii）.

Proof.Suppose that A=｛1，a｝for some a∈SE（S）and a2∈E（S）.Let e=a2.Then e/=1 by 1 is irreducible.Also，by S is a completely regular semigroup，we have Ha（S）is a group.So e=a2∈Ha（S），which implies that ae=ea=a.Thus，we have

（i）It is obvious that A2=｛1，a，e｝is idempotent and A is not idempotent；

（ii）A2｛1，e｝=｛1，a，e｝｛1，e｝=｛1，a，e｝=A2.Assume that there exists an f∈E（S）｛1｝such that A2｛1，f｝=A2.Then

and so f=e.That is to say e is the unique element in E（S）｛1｝such that A2｛1，e｝=A2；

（iii）A｛1，e｝=｛1，a｝｛1，e｝=｛1，a，e｝=A2；

（iv）If A2=UV for some U，V∈P（S）satisfying U/=｛1｝and V/=｛1｝，then 1∈U and 1∈V since 1∈A2and 1 is irreducible.It follows that

｛1｝⊆U=U1⊆UV=A2=｛1，a，e｝，｛1｝⊆V=1V⊆UV=A2=｛1，a，e｝.

Thus we have

and

Since A2=UV，it is not hard to verify that one of the eight cases in（iv）holds.

Conversely，suppose that A∈P（S）satisfies（i）-（iv）.Consider the following cases：

（i）If there exists a non-idempotent element b in A2，then it is easy to verify that

Also，we have that A2/=｛1，b｝since A2is idempotent and｛1，b｝is not idempotent，and A2｛b2｝/=｛1｝since b∈A2｛b2｝.It follows that A=｛1，b｝by（iv），and so A2=｛1，b，b2｝. Since A2is idempotent and b∈A2，we have

and so b3=b or b3=b2，which implies that b4=b2，i.e.，b2∈E（S）.Thus A=｛1，b｝for some b∈SE（S）and b2∈E（S）；

（ii）If A2is a singleton set，then A=A2since A=A1⊆ A｛1，e｝=A2by（iii），contradicting（i）；

（iii）If A2is a band and|A2|=2，letting A2=｛e，f｝，where e/=f and e/=1，then it is easy to see that

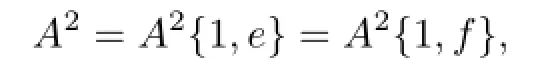
which implies that f=1 by（ii），that is，A2=｛1，e｝.Since

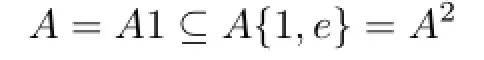
by（iii），we have

in either case，A is idempotent，contradicts（i）.

（iv）If A2is a band and|A2|≥3，letting e，f∈A2such that e/=f and e/=1，f/=1，then

contradicts（ii）.The proof is completed.

Corollary 2.1Let S，S′∈C，and ψ be an isomorphism from P（S）to P（S′）.Let e∈E（S）｛1｝，and a∈SE（S）such that a2∈E（S）.Then ψ（｛1，e｝）=｛1，f｝for some f∈E（S′）｛1｝，and ψ（｛1，a｝）=｛1，a′｝for some a′∈S′E（S′）such that a′2∈E（S′）.

Proof.It follows immediately by Lemmas 2.3 and 2.4.

Proposition 2.1Let S，S′be completely regular semigroups，and ψ be an isomorphism from P（S）to P（S′）.If e∈E（S）and A=ψ（｛e｝），then the following statements are true：

（i）If B∈P（S′）such that B2=A，then B∈HA（P（S′））；

（ii）If B∈P（S′）such that B⊆A and B2=A，then B=A；

（iii）A is a completely regular subsemigroup of S′；

（iv）a2∈E（S′）for any a∈A.

Proof.（i）Let e∈E（S）and A=ψ（｛e｝）.Suppose that B∈P（S′）satisfies B2=A. Assume that K∈P（S）such that ψ（K）=B.Then

and so K2=｛e｝.

Next，we show that K⊆He（S）and|K|=1.

Indeed，for any k∈K，we have k2∈K2=｛e｝，i.e.，k2=e.Since S is a completely regular semigroups，we know that Hk（S）is a subgroup of S and so

Therefore，

This shows that

Also，for any k1，k2∈K，we have

and so

which implies that k1=k2.Thus|K|=1.

Notice that a singleton member of P（S）is identified with the element it contains，we have

and so

（ii）Suppose that B∈P（S′）such that B⊆A and B2=A.Then

by（i）.It follows that

hence

（iii）As an idempotent in P（S′），A is a subsemigroup of S′.To prove that A is completely regular，it suffices to show that the order of every member in A is finite，that is，for any a∈A，there exists some positive integer n such that an∈E（S′）.Suppose，by a contradiction，that there exists a b∈A such that its order is infinite.Set C=A｛b3｝.Then C/=A.

Next we show that C2=A.Clearly C2⊆A2=A.Conversely，for any d∈A，since A=A2，we have d=gh for some g，h∈A.Consider the following cases：

（1）g，h∈C.Then it is clear that d=gh∈C2；

（2）g∈C but h=b3.Then d=gh=gb3=gb·b2=gb2·b.

If gb=gb2，then gb3=gb2=gb and so d=gh=gb3=gb∈C2.

If gb/=gb2，then either gb/=b3or gb2/=b3，that is to say，gb∈C or gb2∈C，and so d∈C2；

（3）h∈C but g=b3.The proof is similar to the proof of（2）；

（4）g=b3and h=b3.Then d=gh=b6=b2·b4∈C2.

Thus d∈C2and so A⊆C2.Therefore C2=A，contradicting（ii）.This shows that the order of every member in A is finite and so A is a completely regular subsemigroup of S′.

（iv）Suppose，by a contradiction，that there exists a c∈A such that c2/∈E（S′）.Let ecbe the identity element of group Hc（S′）and D=A｛ec｝.Then D/=A by（iii）.

Next we show that D2=A.Clearly D2⊆A2=A.Conversely，we have ec=cc-1∈D2and D2contains all subgroups of A other than Hec（A）.Moreover，if h∈Hec（A）｛ec｝，then

Since c2/∈E（S′），i.e.，c2/=ec，we have c/=c-1and so hc/=hc-1.It follows that either

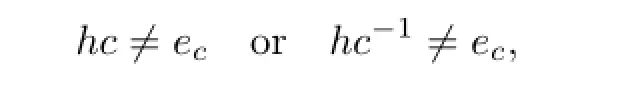
that is to say，either

and so

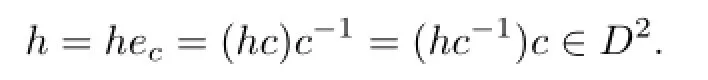
Thus we have shown that D2=A，contradicting（ii）.Therefore，

Lemma 2.5Let S，S′∈C and ψ be an isomorphism from P（S）to P（S′）.Let e∈E（S）and A=ψ（｛e｝）.Then A⊆E（S′）.

Proof.Suppose that there exists a a∈A such that a/∈E（S′），i.e.，a/=a2.Then a2∈E（S′）by Proposition 2.1（iv）.Also，it is easy to verify that

and so

By Corollary 2.1，we have that ψ-1（｛1，a｝）=｛1，b｝for some b∈SE（S）such that b2∈E（S）.It follows that

and so

implying

i.e.，

a contradiction.Therefore，A⊆E（S′），as required.

Theorem 2.1C satisfies the strong isomorphism property.

Proof.Let S，S′∈C，and ψ be an isomorphism from P（S）to P（S′）.Let e∈E（S）and A=ψ（｛e｝）.We have A⊆E（S′）by Lemma 2.5.

To show that C satisfies the strong isomorphism property，i.e.，ψ and ψ-1map singletons to singletons，it suffices to show that|A|=|ψ（｛e｝）|=1 by Lemma 2.1.

Suppose，by a contraction，that|A|=|ψ（｛e｝）|≥2.Then there exist f，g∈A such that f/=g.Consider the following two cases：

Case 1.If fg∈｛f，g｝，then it is easy to verify that

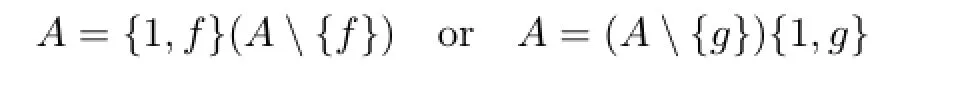
and so

It follows that

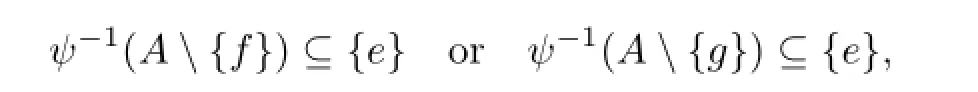
since 1∈ψ-1（｛1，f｝）and 1∈ψ-1（｛1，g｝）by Corollary 2.1，and so ψ-1（A｛f｝）=｛e｝or ψ-1（A｛g｝）=｛e｝，that is，A=A｛f｝or A=A｛g｝，a contradiction.

Case 2.If fg/∈｛f，g｝，then we have

since A⊆E（S′），contradicting Proposition 2.1（ii）.

Thus we have shown that|A|=|ψ（｛e｝）|=1.This completes the proof.

AcknowledgmentThe authors are particularly grateful to Professor Zhao Xian-zhong for his helpful discussions and suggestions during preparation for this article.

References

［1］Tamura T.Unsolved Problems on Semigroups.Kyoto Surikaiseki Kenkyusho：Semin.Math. Sci.，1967，82：33-35.

［2］Mogiljanskaja E M.Non-isomorphic semigroups with isomorphic semigroups of subsets.Semigroup Forum，1973，6：330-333.

［3］Crvenkovi´c S，Dolinka I，Vinˇci´c M.Involution semigroups are not globally determined.Semigroup Forum，2001，62：477-481.

［4］Tamura T，Shafer J.Power semigroups.Math.Japonica，1967，12：25-32.

［5］McCarthy D J，Hayes S D L.Subgroups of the power semigroup of a group.J.Combin.Theory Ser.A，1973，14：173-186.

［6］Tamura T.Power semigroups of rectangular groups.Math.Japonica，1984，4：671-678.

［7］Tamura T.Isomorphism problem of power semigroups of completely 0-simple semigroups.J. Algebra，1986，98：319-361.

［8］Tamura T.On the Recent Results in the Study of Power Semigroups.Semigroups and Their Applications.Netherlands：Springer，1987：191-200.

［9］Gould M，Iskra J A，Tsinakis C.Globally determined lattices and semilattices.Algebra Universalis，1984，19：137-141.

［10］Kobayashi Y.Semilattices are globally determined.Semigroup Forum，1984，29：217-222.

［11］Gould M，Iskra J A.Globally determined classes of semigroups.Semigroup Forum，1984，28：1-11.

［12］Gould M，Iskra J A.Globals of completely regular periodic semigroups.Semigroup Forum，1984，29：365-374.

［13］Burris S，Sankappanavar H P.A Course in Universal Algebra.Berlin：Springer-Verlag，2000.

［14］Howie J M.Fundamentals of Semigroup Theory.Oxford：Clarendon Press，1995.

［15］Mario P，Norman R R.Completely Regular Semigroups.New York：A Wiley-Interscience Publication，1999.

［16］Jorge A.Finite Semigroup and Universal Algebra.Singapoer：World Scientific Publishing Co.，1994.

10.13447/j.1674-5647.2015.03.04

date：Aug.3，2013.

The NSF（11261021）of China and the NSF（20142BAB201002）of Jiangxi Province.

.

E-mail address：molihuaqian@163.com（Wu Q Q），ganaiping78@163.com（Gan A P）.