Pseudopolarity of Generalized Matrix Rings over a Local Ring

Yin Xiao-Bin anD Dou Wan

（College of Mathematics and Computer Science，Anhui Normal University，Wuhu，Anhui，241000）

Communicated by Du Xian-kun

Pseudopolarity of Generalized Matrix Rings over a Local Ring

Yin Xiao-Bin anD Dou Wan

（College of Mathematics and Computer Science，Anhui Normal University，Wuhu，Anhui，241000）

Communicated by Du Xian-kun

pseudopolar ring，local ring，generalized matrix ring

2010 MR subject classification：16E50

Document code：A

Article ID：1674-5647（2015）03-0211-11

1　Introduction

Throughout this paper all rings are associative with unity.We adopt the following notations from Koliha and Patricio［1］.For an element a∈R，the commutant and double commutant of a in R are defined by

and

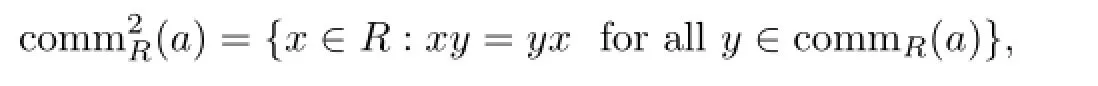
respectively，if there is no ambiguity，we simply use comm（a）and comm2（a）for short.LetIf a∈Rqnilthen a is said to be quasinilpotent（see［2］）.An element a is quasipolar（see［1］）if there exists a p∈R with p=p2such that

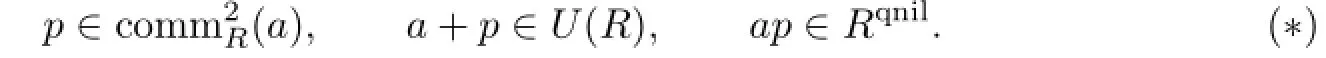
Any idempotent p satisfying the above conditions is called a spectral idempotent of a，which is uniquely determined by the element a if it exists.This term is borrowed from spectral theory in Banach algebras.A ring is said to be quasipolar（see［3］）if every element in R is quasipolar.It was proved in［3］that all local rings and strongly π-regular rings are quasipolar and quasipolar rings are strongly clean.If the condition ap∈Rqnilin（∗）is replaced by akp∈J（R）for k≥1，then the element a∈R is called pseudopolar（see［4］），and in this case，the idempotent p is called a strongly spectral idempotent of a and denoted by aΠ.R is called pseudopolar if all elements of R are pseudopolar.It was shown in［5］that both uniquely strongly clean rings and strongly π-regular rings are pseudopolar，and that pseudopolar rings are quasipolar.It was also proved in［5］that for abelian rings，pseudopolar rings coincide with semiregular rings.

Let R be a ring，and s∈R be central.Following Krylov［6］，we use Ks（R）to denote the setwith operations as follows：

The element s is called the multiplier of Ks（R）.The set Ks（R）becomes a ring with these operations and can be viewed as a special kind of Morita context.A Morita context（A，B，M，N，ψ，φ）consists of two rings A and B，two bimodulesAMB，BNAand a pair of bimodule homomorphisms

which satisfy the following associativity：

Some properties of the ring Ks（R）were studied comprehensively in［7］.And in［9-10］the strong cleanness of the generalized matrix ring Ks（R）over a local ring was studied. The quasipolarity of the generalized matrix ring Ks（R）over a commutative local ring was discussed in［11］.

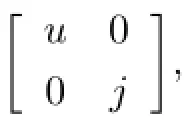
（1）Ks（R）is a pseudopolar ring；

（2）For any u，v∈U（R）and w∈J（R），the element t2-（u+w）t+（uw-sv）has a right root in U（R）and the element t2-（u+w）t+（wu-sv）has a right root in J（R）；

（3）For any u，v∈U（R）and w∈J（R），the element t2-（u+w）t+（uw-sv）has a left root in J（R）and the element t2-（u+w）t+（wu-sv）has a right root in J（R）；

We write Mn（R）（resp.，Tn（R））for the ring of all（resp.，all upper triangular）n×n matrices over the ring R.The symbols U（R），C（R），Rniland J（R）stand for the group of units，the set of all central elements，the set of all nilpotent elements，the Jacobson radical of R，respectively.For a prime integer p，Z（p）denotes the localization of Z at p.

2　Generalized Matrix Rings over a Local Ring

Example 2.1Idempotents，units，nilpotents，and J（R）of a ring R are pseudopolar.

Proof.Let e2=e∈R，u∈U（R），a∈R with ak=0 for some k≥1 and b∈J（R）.Write

p=1-e，0，1，1，respectively.Then the claim follows from a routine computation.

Lemma 2.1［7］Let R be a ring with s∈C（R），and J=J（R）.Then

（2）If R is a local ring with s∈J，then

if and only if a，b∈U（R）.

Lemma 2.2Let R be a local ring，and A∈Ks（R）.Then the following statements are equivalent：

（1）Ak∈J（Ks（R））for some k≥2；

（2）A2∈J（Ks（R））.

Proof.（1）⇒ （2）.If s∈U（R），Ks（R）～=M2（R）.According to Lemma 3.3 in［12］the result holds.We only need to show that if s∈J（R）and Ak∈J（Ks（R））for any k≥2，then A2∈J（Ks（R））.Assume that Ak∈J（Ks（R））.Then there exists an n∈N such that 2n＞k.This gives A2n∈J（Ks（R））.Without loss of generality，let

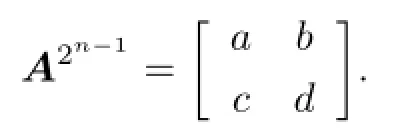
Then

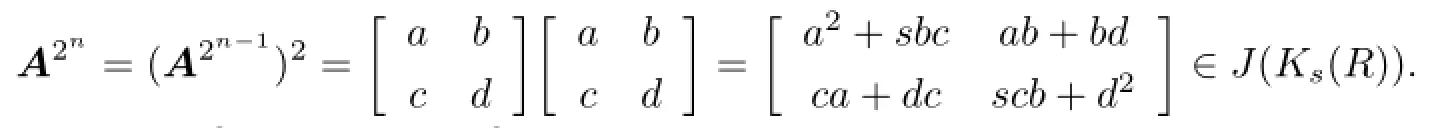
By Lemma 2.2，a2+sbc，scb+d2∈J（R）.From s∈J（R）we can obtain sbc，scb∈J（R）and a2，d2∈J（R）.So a，d∈J（R）.Therefore，∈J（Ks（R）），which implies A2∈J（Ks（R））.

（2）⇒（1）is trivial.

Remark 2.1Let R be a local ring.By Lemma 2.2，we conclude that a matrix A ∈Ks（R）is pseudopolar if and only if there exists awith P=P2such that A+P∈U（Ks（R））and A2P∈J（Ks（R））.

Proposition 2.1Let R be a ring and s∈C（R）.Then A∈Ks（R）is pseudopolar if and only if V AV-1∈Ks（R）is pseudopolar for some V∈U（Ks（R））.

Proof.It is sufficient to show that if A ∈Ks（R）is pseudopolar，then so is V AV-1. Assume that E∈Ks（R）is the strongly spectral idempotent of A.Write

Then

Therefore

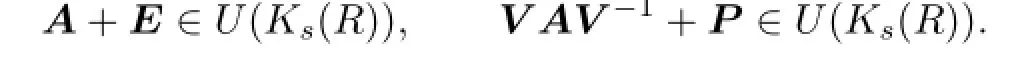
From AkE∈J（Ks（R）），one gets that

Next，we show that P∈comm2（V AV-1）.For any B∈comm（V AV-1），we obtain

So V-1BV∈comm（A）.Since E∈comm2（A），it follows that

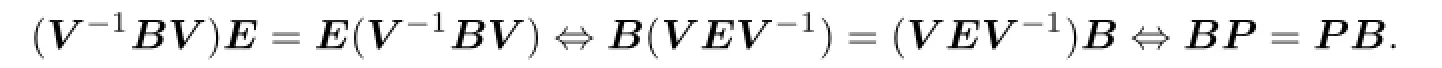
So P∈comm2（V AV-1）.This proves that V AV-1∈Ks（R）is pseudopolar.

The following results are elementary.

Lemma 2.3Let R be a local ring and A∈Ks（R）.Then

（1）A is pseudopolar with AΠ=0 if and only if A is invertible；

（2）A is pseudopolar with AΠ=I if and only if A2∈J（Ks（R））.

Theorem 2.1Let R be a local ring，and A∈Ks（R）with A/∈U（Ks（R））and A2/∈J（Ks（R））.Suppose that the matrix A is pseudopolar.Then AΠis an idempotent diagonal matrix if and only if A is diagonal and one diagonal entry of A is in U（R），and the other is in J（R）.Proof.Assume that A is a diagonal matrix.Since A/∈U（Ks（R））and A2/∈J（Ks（R）），one diagonal entry of A is in U（R），and the other is in J（R）.Without loss of generality，let

Write E=AΠ=（eij）.Since AE=EA，we have

Then ue12=e12j，je21=e21u.Let

Then

So E∈comm2（A）implies that

It follows that

Combining these with E2=E，we have

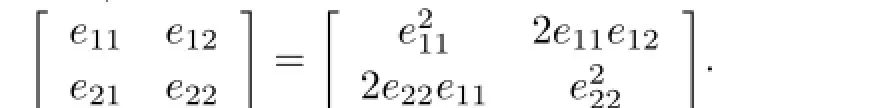
Thus eiiare idempotents for i=1，2.Since R is local，eii=0 or 1.It is easy to see that e12=e21=0.Note that A+E is a unit，we get e22=1.If e11=1，then E=I.By Lemma 2.3，A2∈J（Ks（R）），a contradiction.This shows that

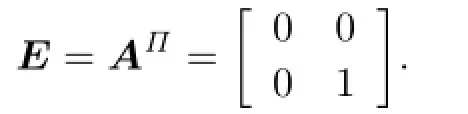
Conversely，assume that

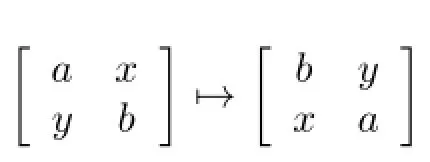
Theorem 2.2Let R be a local ring，u∈U（R）and j∈J（R）.Then the following statements are equivalent：

（3）The endomorphisms lu-rjand lj-ruare injective.

Proof.（1）⇔（2）.By Lemma 2.4，the result follows.

（3）⇒（2）.Write

Then

We check E∈comm2（A）.Thus ub12-b12j=0 and jb21-b21u=0.By the hypothesis，b12=b12=0.So EB=BE，as required.Therefore，A is pseudopolar in Ks（R）.

Lemma 2.5［4］Let R be a local ring，s∈C（R）and let E be a non-trivial idempotent of Ks（R）.

Proof.The sufficiency follows from Proposition 2.1，Lemma 2.3 and Theorem 2.2.

We now show the necessity.Suppose that A is pseudopolar in Ks（R）.By Remark 2.1，there exists an E∈commwith E=E2such that W=A+E∈U（Ks（R））and A2E∈J（Ks（R））.If E=0 or E=I2，by Lemma 2.3，A∈U（Ks（R））or A2∈ J（Ks（R）），respectively.Hence，by Lemma 2.5，eitherIfby Proposition 2.1，there exists a P∈U（Ks（R））such that PAP-1is pseudopolar with

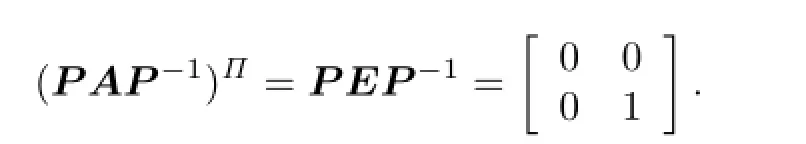
By Theorem 2.1，one has

A local ring R is called co-leached（see［5］），if for any j∈J（R）and u∈U（R），the abelian group endomorphisms lu-rjand lj-ruof R are injective.

Theorem 2.4Let R be a co-bleached local ring with s∈J（R）∩C（R），and

The following statements are equivalent：

（1）A is pseudopolar in Ks（R）；

（2）t2-（vuv-1+w）t+（vuv-1w-sv）has a right root in U（R）and t2-（u+w）t+（wu-sv）has a right root in J（R）.

Proof.（1）⇒（2）.Since A/∈U（Ks（R））and A2/∈J（Ks（R）），by Theorem 2.3，there exist [

such that

That is，

By Lemma 2.1，we have a，b∈U（R），and so λ1∈U（R）and λ2∈J（R）by（2.1）and（2.4）.

Note that x，y∈U（R）by（2.2）and（2.3）.Hence

Moreover，we obtain

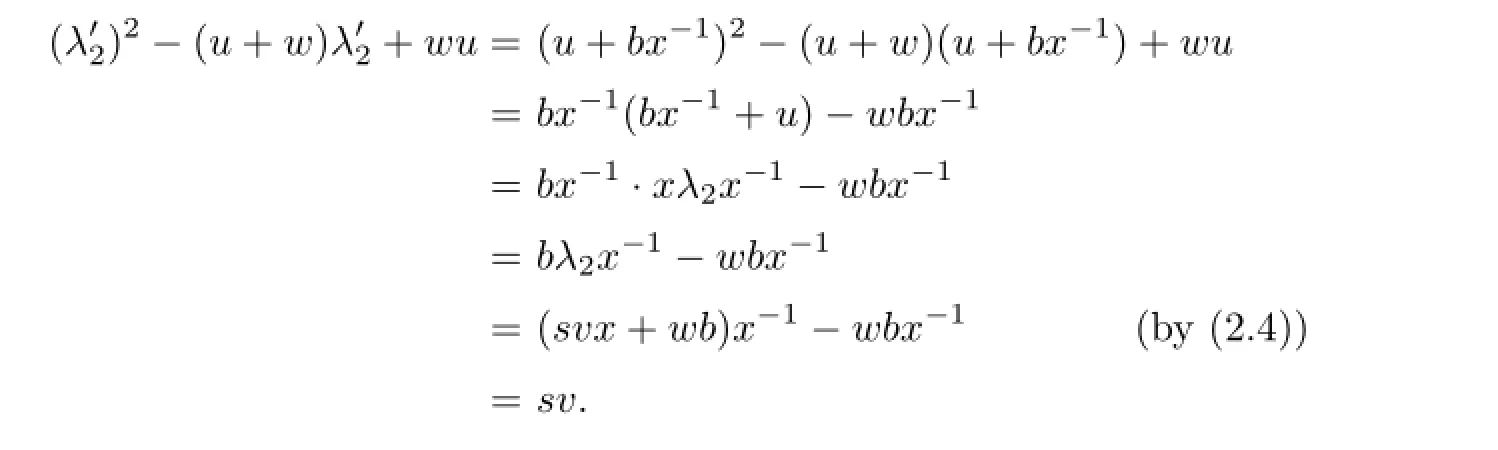
and

（2）⇒（1）.Suppose that λ1is a right root of t2-（vuv-1+w）t+（vuv-1w-sv）in U（R）and λ2is a right root of t2-（u+w）t+（wu-sv）in J（R）.Then，by Lemma 2.1，

and a direct calculation shows that

Hence A is pseudopolar in Ks（R）by Theorem 2.3.

Lemma 2.1（2），we have either a∈U（R）and d∈J（R），or a∈J（R）and d∈UR）.

Case 1.a∈U（R）and d∈J（R）.We have

Assume that b∈U（R）.Then

If c∈U（R），then it is done.Suppose that c∈J（R）.Then

Case 2.a∈J（R）and d∈UR）.It is similar to verify that

Lemma 2.6［6］Let R be a ring and let f（t）=：t2-at+b∈R［t］.Then

（1）c∈R is a left root of f（t）if and only if a-c is a right root of f（t）.In this case，f（t）=（t-c）（t-a+c）∈R［t］；

（2）If a∈U（R），then f（t）has a left（resp.right）root in U（R）if and only if f（t）has a right（resp.left）root in J（R）.

Theorem 2.6Let R be a co-bleached local ring with s∈J（R）∩C（R）.The following statements are equivalent：

（1）Ks（R）is a pseudopolar ring；

（2）For any u，v∈U（R）and w∈J（R），t2-（u+w）t+（uw-sv）has a right root in U（R）and t2-（u+w）t+（wu-sv）has a right root in J（R）；

（3）For any u，v∈U（R）and w∈J（R），t2-（u+w）t+（uw-sv）has a left root in J（R）and t2-（u+w）t+（wu-sv）has a right root in J（R）；

Proof.（1）⇒（4）.It is obvious.

（4）⇒（2）.Let u，v∈U（R）and w∈J（R），

Since v-1uv∈U（R），A and B are pseudopolar in Ks（R）by（2.4）.Hence，by Theorem 2.4，t2-（u+w）t+（uw-sv）has a right root in U（R）and t2-（u+w）t+（wu-sv）has a right root in J（R）.

（2）⇔（3）.It follows from Lemma 2.6.

3　Special Cases

Lemma 3.1［11］Let R be a commutative local ring.The following statements are equivalent for A∈Ks（R）：

（1）detsA∈J（R）and trA∈J（R）；

（2）A2∈J（Ks（R））；

（3）A is quasinilpotent in Ks（R）.

By Lemma 3.1，we get the following result immediately.

Remark 3.1Let R be a commutative local ring.Then a matrix A∈Ks（R）is pseudopolar if and only if A is quasipolar.

Lemma 3.2Let R be a commutative local ring，and A∈Ks（R）with detsA∈J（R）. Then trA∈J（R）if and only if A is pseudopolar with I2the strongly spectral idempotent.

Corollary 3.1Let R be a commutative local ring with R/J（R）～=Z2.Then A∈Ks（R）with detsA∈J（R）and dets（A-I2）∈U（R）is pseudopolar.

Proof.Let A ∈Ks（R）such that detsA ∈J（R）and dets（A-I2）∈U（R）.Since R/J（R）～=Z2，trA=1+detsA-dets（A-I2）∈J（R）.In view of Lemma 2.3，A is pseudopolar with the strongly spectral idempotent I2.

Lemma 3.3［11］Let R be a commutative local ring with s∈R and A∈Ks（R）such that neither A∈U（Ks（R））nor A∈（Ks（R））qnil.Then the following statements are equivalent：

（1）A is quasipolar in Ks（R）；

（2）The equation x2-tr（A）x+detsA=0 is solvable in R.

Lemma 3.4［13］Let R be a commutative local ring，and for any p，q∈R，let t=p2-4q.

（1）If the equation x2-px+q=0 is solvable in R，then t is a square.The converse holds if 2∈U（R）；

（2）Suppose that J（R）=2R and R is a domain.Let p∈U（R），q∈J（R）such that t is a square，then the equation x2-px+q=0 is solvable in R.

Theorem 3.1Let R be a commutative local ring.If A∈Ks（R）is pseudopolar，then exactly one of the following holds：

（1）A is invertible in Ks（R）；

（2）detsA∈J（R）and trA∈J（R）；

（3）detsA∈J（R），trA∈U（R）and（tr（A））2-4detsA=u2for some u∈U（R）.

Proof.Let A∈Ks（R）be pseudopolar.In view of Lemma 2.3，we assume that detsA∈J（R）and trA∈U（R），and so（trA）2-4detsA∈U（R）.By Theorem 2.6，the equation x2-trAx+detsA=0 is solvable in R.Thus by Remark 3.1 and Lemma 3.3，we have（trA）2-4detsA=u2for some u∈U（R）.

Corollary 3.2Let R be a commutative local ring such that either J（R）=2R and R is a domain or 2∈U（R）.Then A∈Ks（R）is pseudopolar if and only if exactly one of the following holds：

（1）A is invertible in Ks（R）；

（2）detsA∈J（R）and trA∈J（R）；

（3）detsA∈J（R），trA∈U（R）and（trA）2-4detsA=u2for some u∈U（R）.

Proof.The necessity follows from Theorem 3.1.

We now show the sufficiency.Let A∈Ks（R）.As before，we assume that detsA∈J（R）and trA∈U（R）.Since（trA）2-4detsA=u2，the equation x2-trAx+detsA=0 is solvable in R by Lemma 3.4.In view of Remark 3.1 and Lemma 3.3，A∈Ks（R）is pseudopolar.

Corollary 3.3Let R=Z（p）.Then A∈Ks（R）is pseudopolar if and only if exactly one of the following holds：

（1）A is invertible in Ks（R）.

（2）detsA∈J（R）and trA∈J（R）.

（3）detsA∈J（R），trA∈U（R）and（trA）2-4detsA=u2for some u∈U（R）.

References

［1］Koliha J J，Patricio P.Elements of rings with equal spectral idempotents.Asut.Math.Soc.，2002，72：137-152.

［2］Harte R E.Strongly clean matrix rings over commutative local rings.Pure Appl.Algebra，2008，212：281-296.

［3］Zhou Y Q，Chen J L.On quasipolar rings.Algebra Colloq.，2012，19：683-692.

［4］Wang Z，Chen J L.Pseudo Drazin inverses in associative rings and Banach algebra.Linear Algebra Appl.，2012，473：1332-1345.

［5］Huang Q H，Tang G H，Zhou Y Q.Quasipolar property of generalized matrix rings.Comm. Algebra，2013，accepted.

［6］Krylov P A.Isomorphism of generalized matrix rings.Algebra Logic.，2008，47（4）：258-262.

［7］Krylov P A，Tuganbaev A A.Modules over formal matrix rings.J.Math.Sci.，2012，171（2）：248-295.

［8］Tang G H，Li C，Zhou Y Q.On Morita contexts，2011，preprint.

［9］Borooah G，Diesl A J，Dorsey T J.Strongly clean matrix rings over commutative local rings. Pure Appl.Algebra，2008，212（1）：281-296.

［10］Tang G H，Zhou Y Q.Strong cleanness of generalized matrix rings over a local ring.Linear Algebra Appl.，2012，473（10）：2546-2559.

［11］Gurgun O，Halicioglu S，Harmanci A.Quasipolarity of generalized matrix rings.arXiv：1303.3173vl［math.RA］.Submitted on 13 March 2013.

［12］Cui J，Chen J L.Pseudopolar matrix rings over local rings.J.Algebra.Appl.，2013，revised.

［13］Cui J，Chen J L.When is a 2×2 matrix ring over a commutative local ring quasipolar？Comm. Algebra，2011，39（9）：3212-3221.

10.13447/j.1674-5647.2015.03.03

date：July 25，2013.

The NSF（10871024，11326062）of China.

E-mail address：xbyinzh@mail.ahnu.edu.cn（Yin X B）.