Notes on Automorphisms of Prime Rings

Huang Shu-liang

（Department of Mathematics，Chuzhou University，Chuzhou，Anhui，239012）

Communicated by Du Xian-kun

Notes on Automorphisms of Prime Rings

Huang Shu-liang

（Department of Mathematics，Chuzhou University，Chuzhou，Anhui，239012）

Communicated by Du Xian-kun

Let R be a prime ring，L a noncentral Lie ideal and σ a nontrivial automorphism of R such that usσ（u）ut=0 for all u∈L，where s，t are fixed non-negative integers.If either charR＞s+t or charR=0，then R satisfies s4，the standard identity in four variables.We also examine the identity（σ（［x，y］）-［x，y］）n= 0 for all x，y∈I，where I is a nonzero ideal of R and n is a fixed positive integer.If either charR＞n or charR=0，then R is commutative.

prime ring，Lie ideal，automorphism

2010 MR subject classification：16N60，16U80，16W25

Document code：A

Article ID：1674-5647（2015）03-0193-06

1　Introduction

The standard identity s4in four variables is defined as follows：

where（-1）τis the sign of the permutation τ of the symmetric group of degree 4.In the following，unless stated otherwise，R always denotes a prime ring with its center Z（R）and Martindale quotient ring Q.The center of Q，denoted by C，is called the extended centroid of R（we refer the reader to［1］for these terminologies）.For any x，y∈R，the symbol［x，y］stands for the commutator xy-yx.An additive subgroup U of R is said to be a Lie ideal of R if［u，r］∈U for all u∈U and r∈R.For nonempty subsets A，B of R，let［A，B］be the additive subgroup generated by all the elements of the form［a，b］with a∈A and b∈B. Recall that a ring R is prime if for any a，b∈R，aRb=（0）implies a=0 or b=0，and is semiprime if for any a∈R，aRa=（0）implies a=0.An additive mapping d：R→R is called a derivation if d（xy）=d（x）y+xd（y）holds for all x，y∈R.Starting from thisdefinition，Breˇsar［2］first introduced the definition of generalized derivations：An additive mapping F：R→R is called a generalized derivation if there exists a derivation d：R→R such that F（xy）=F（x）y+xd（y）holds for all x，y∈R，and d is called the associated derivation of F.Hence，the concept of generalized derivations covers the concepts of both derivations and left multipliers（i.e.，the additive mappings satisfying F（xy）=F（x）y for all x，y∈R）.Basic examples are derivations and generalized inner derivations（i.e.，mappings of the typefor some a，b∈R）.We prefer to call such mappings generalized inner derivations for the reason that they present a generalization of the concept of inner derivations（i.e.，mappings of the formfor some a∈R）.

This paper is included in a line of investigation concerning the relationship between the global structure of a ring R and the behaviors of some additive mappings defined on R that satisfy certain special identities.A well-known result of Herstein［3］states that if ρ is a right ideal of R such that un=0 for all u∈ρ，where n is a fixed positive integer，then ρ=0. Chang and Lin［4］considered the situation when d（u）un=0 for all u∈ρ，where d is a nonzero derivation of R.Dhara and De Filippis［5］studied the case when usH（u）ut=0 for all u∈L，where L is a noncommutative Lie ideal of R，H is a generalized derivation of R and s，t are fixed non-negative integers.More precisely，they proved the following：Let R be a prime ring，H a nonzero generalized derivation of R and L a noncommutative Lie ideal of R.Suppose that usH（u）ut=0 for all u∈L.Then R satisfies s4，the standard identity in four variables.On the other hand，Carini and De Filippis［6］proved that if R is a prime ring with charR/=2 and such that［d（u），u］n=0 for all u∈L，where L is a noncentral Lie ideal and d is a nonzero derivation of R，then R is commutative.Wang［7］also discussed the identity［σ（u），u］n=0 replacing the derivation d by an automorphism σ of R and obtained that R satisfies s4.Motivated by the previous results，our first objective in this note is to study the identity usσ（u）ut=0 for all u∈L，where L is a noncentral Lie ideal and σ is an automorphism of the prime ring R，and then describe the structure of R.

During the past few decades，there has been an ongoing interest in concerning the relationship between the commutativity of a ring and the existence of certain specific types of derivations（see［8-9］for a partial bibliography，where further references can be found）.The first result in this direction is due to Posner［10］who proved that a prime ring R admitting a nonzero derivation d such that［d（x），x］∈Z（R）for all x∈R must be commutative.This result was subsequently refined and extended by a number of authors，and we refer the readers to［11-13］for further references.In 1992，Daif and Bell［14］showed that if in a semiprime ring R there exist a nonzero ideal I of R and a derivation d such that d（［x，y］）=［x，y］for all x，y∈I，then I⊆Z（R）.If R is a prime ring，this implies that R is commutative.De Filippis［15］obtained the commutativity of prime rings when the derivation d is replaced by an automorphism σ.Later，Quadri et al.［16］extended Daif's result to generalized derivations.Ashraf and Ali［17］proved that R is commutative in the setting of left multipliers.In 2002，De Filippis［18］obtained the following result：Let R be a prime ring without non-zero nil right ideal，d a nonzero derivation of R，and I a non-zero ideal of R.If for any x，y∈I，there exists n=n（x，y）≥1 such that（d（［x，y］）-［x，y］）n=0，then R is commutative.Itis natural to ask what we can say about the commutativity of rings satisfying the identity（σ（［x，y］）-［x，y］）n=0 for an automorphism of the ring.Our second object in this paper is to investigate the above identity in prime rings and to obtain the commutativity of prime rings.

2　Main Results

Theorem 2.1Let R be a prime ring，L a noncentral Lie ideal and σ a nontrivial automorphism of R such that usσ（u）ut=0 for all u∈L，where s，t are fixed non-negative integers.If either charR＞s+t or charR=0，then R satisfies s4，the standard identity in four variables.

Proof.Suppose that R does not satisfy s4.It follows from pages 4-5 in［3］，Lemma 2 in［19］and Theorem 4 in［20］that there exists a nonzero two-sided ideal I of R such that 0/=［I，R］⊆L.In particular，［I，I］⊆L.Hence，without loss of generality，we may assume that L=［I，I］.By assumption，we have

which can be rewritten as

By Main Theorem in［21］，we divide the proof into two cases.

Case 1.Let σ be Q-outer.Since either charR＞s+t or charR=0，by Theorem 3 in［22］，we obtain

In particular，let

Then it follows from Theorem 2 in［23］that R is commutative and so L is central，a contradiction.

Case 2.If σ is Q-inner，then there exists an invertible element b∈Q such that

We note that b/∈C since σ/=1R，the identity map on R.By Theorem 2 in［24］，I，R and Q satisfy the same generalized polynomial identities（or GPIs in brief），and from（2.1）we have

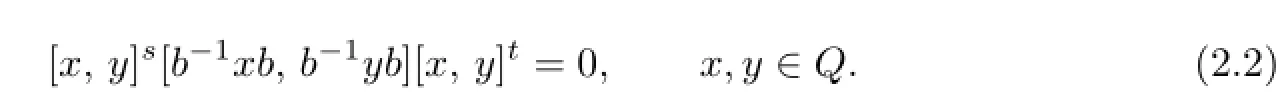
In the case that the center C of Q is infinite，we have

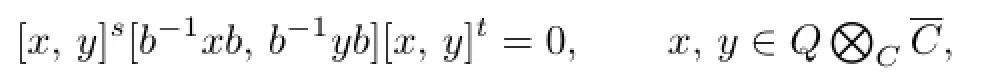
For any given v∈V，we want to show that v and bv are linearly D-dependent.If bv=0，then v and bv are D-dependent.We are done in this case.Suppose that bv/=0，v and bv were D-independent.Then by the density of R，there would exist x，y∈R such that

From（2.2），we can see that

It is a contradiction.From above we have proven that

where αv∈D depends on v∈V.In fact，it is easy to check that αvis independent of the choice of v∈V.Indeed，for any v，w∈V，by the above arguments，there exist αv，αw，αv+w∈D such that

And so

Hence

If v and w are D-independent，then

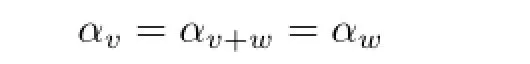
and we are done.Otherwise，suppose that v and w were D-dependent.Let v=λw for some λ∈D.Then

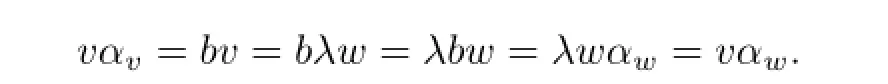
That is，for any v we can choose some αvsuch that αv=αw，where w/=0 and αwwere fixed beforehand.So we conclude that there exists a δ∈D such that bv=vδ for all v∈V. So b=δ∈D=C.It is a contradiction.This completes the proof.

Theorem 2.2Let R be a prime ring，I a nonzero ideal and σ a nontrivial automorphism of R such that

where n is a fixed positive integer.If either charR＞n or charR=0，then R is commutative. Proof.For n=1，it follows from Lemma 1.2 in［15］.Suppose that n≥2 and R were not commutative.We give that

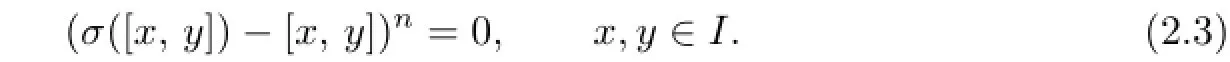
Assume first that σ is Q-outer.Since either charR＞n or charR=0，by Theorem 3 in［22］，we see that

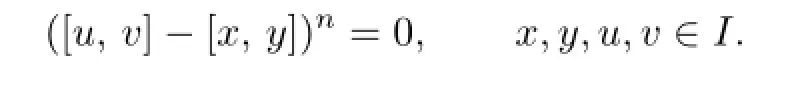
In particular，setting u=0，we have

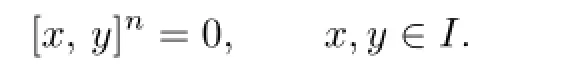
It follows from Theorem 2 in［23］that R is commutative，a contradiction.Suppose now that σ is Q-inner.Then there would exist an invertible element b∈Q-C such that

Suppose that there exists a v∈V such that bv and v are D-independent.Then by the density of R，there exist x，y∈R such that

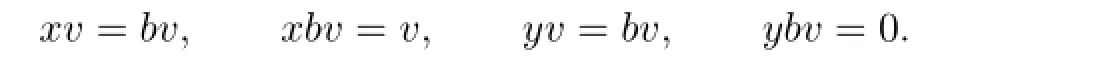
Application of（2.3）yields that

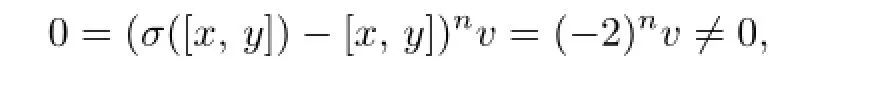
a contradiction.The rest of the proof is the same as the last paragraph of the proof of Theorem 2.1.And hence we can get a contradiction that b∈C.The proof is thereby completed.

The following example demonstrates that R being prime is essential in Theorem 2.2. Example 2.1Set

and

where Z is the ring of all integers.Next，let us define a mapping σ：R→R by

Then it is clear that I is a nonzero ideal of R and σ is a nontrivial automorphism of R. And it is easy to check that（σ（［x，y］）-［x，y］）n=0 for all x，y∈I.However，R is not commutative.

References

［1］Beidar K I，Martindale W S，Mikhalev V.Rings with Generalized Identities.New York：Marcel Dekker Inc.，1996.

［2］Breˇsar M.On the distance of the composition of two derivations to be the generalized derivations.Glasgow Math.J.，1991，33：89-93.

［3］Herstein I N.Topics in Ring Theory.Chicago：Univ.of Chicago Press，1969.

［4］Chang C M，Lin Y C.Derivations on one-sided ideals of prime rings.Tamsui Oxford J.Management Sci.，2001，17（2）：139-145.

［5］Dhara B，De Filippis V.Notes on generalized derivations on Lie ideals in prime rings.Bull. Korean Math.Soc.，2009，46（3）：599-605.

［6］Carini L，De Filippis V.Commutators with power central values on a Lie ideal.Pacific J. Math.，2000，193（2）：269-278.

［7］Wang Y.Power-centralizing automorphisms of Lie ideals in prime rings.Comm.Algebra，2006，34：609-615.

［8］Bell H E，Martindale W S.Centralizing mappings of semiprime rings.Canad.Math.Bull.，1987，30（1）：92-101.

［9］Demir C，Argac N.A result on generalized derivations with Engel conditions on one-sided ideal.J.Korean Math.Soc.，2010，47（3）：483-494.

［10］Posner E C.Derivations in prime rings.Proc.Amer.Math.Soc.，1957，8：1093-1100.

［11］Argac N，Carini L，De Filippis V.An engel condition with generalized derivations on Lie ideals. Taiwanese J.Math.，2008，12：419-433.

［12］De Filippis V.An Engel condition with generalized derivations on multilinear polynomials. Israel J.Math.，2007，162：93-108.

［13］Lee T K.Left annihilators characterized by GPIs.Trans.Amer.Math.Soc.，1995，347（8）：3159-3165.

［14］Daif M N，Bell H E.Remarks on derivations on semiprime rings.Internat.J.Math.Math. Sci.，1992，15：205-206.

［15］De Filippis V.Automorphisms and derivations in prime rings.Rend.Mat.Appl.（7），1999，19：393-404.

［16］Quadri M A，Khan M S，Rehman N.Generalized derivations and commutativity of prime rings.Indian J.Pure Appl.Math.，2003，34（9）：1393-1396.

［17］Ashraf M，Ali S.On left multipliers and the commutativity of prime rings.Demonstratio Math.，2008，41（4）：763-771.

［18］De Filippis V.On a subset with nilpotent values in a prime ring with derivation.Boll.Un. Mat.Ital.B（7），2002，8（5）：833-838.

［19］Di Vincenzo O M.On the n-th centralizers of a Lie ideal.Boll.Un.Mat.Ital.A（7），1989，3：77-85.

［20］Lanski C，Montgomery S.Lie structure of prime ring of characteristic 2.Pacific J.Math.，1972，42（1）：117-136.

［21］Chuang C L.Differential identities with automorphisms and anti automorphisms I.J.Algebra，1992，149：371-404.

［22］Chuang C L.Differential identities with automorphisms and anti automorphisms II.J.Algebra，1993，160：130-171.

［23］Herstein I N.Center-like elements in prime rings.J.Algebra，1979，60：567-574.

［24］Chuang C L.GPIs having coefficents in Utumi quotient rings.Proc.Amer.Math.Soc.，1988，103（3）：723-728.

［25］Erickson J S，Martindale W S，Osborn J M.Prime nonassociative algebras.Pacific J.Math.，1975，60（1）：49-63.

［26］Martindale W S.Prime rings satisfying a generalized polynomial identity.J.Algebra，1969，12：176-584.

［27］Jacobson N.Structure of Rings.Provindence，RI，USA：Amer.Math.Soc.，1964.

10.13447/j.1674-5647.2015.03.01

date：Sept.16，2011.

The NSF（1408085QA08）of Anhui Province，the Natural Science Research Foundation（KJ2014A183）of Anhui Provincial Education Department，and Anhui Province College Excellent Young Talents Fund Project（2012SQRL155）of China.

E-mail address：shulianghuang@163.com（Huang S L）.