一个应用混合基算法的余数系统后置转换电路设计

黄世洋， 陈奉仪， 姚若河

(华南理工大学电子与信息学院，广州 510640)

一个应用混合基算法的余数系统后置转换电路设计

黄世洋， 陈奉仪， 姚若河*

(华南理工大学电子与信息学院，广州 510640)

针对传统的混合基算法在实现余数系统到二进制系统转换过程中的并行性问题，应用改进的混合基算法，研究与设计了一个基于模集合{2n,2n-1,2n+1-1,2n-1-1}的后置转换电路．模2n-1形式的模加法器采用相对简单的实现结构，使设计的电路避免了只读存储器及时序电路的引入，整个后置转换电路完全由简单组合逻辑及加法器级联实现，缩短了关键路径延时，减小了功率消耗，与已有的相同动态范围余数系统后置转换电路相比，性能优势明显.

混合基算法； 余数系统； 模加法器

余数系统是一个古老的数值表征系统．一个大整数X被划分成几个独立并行运算的小整数，在乘法和加法运算中，各并行模块之间无进位传播，从而减少关键路径的时延，因此对具有大量运算的数字信号处理系统具有广泛的应用前景．在有大量乘法和加法运算的数字信号处理系统中，余数系统不仅可以获得高速的超大规模集成电路实现，而且功耗和面积都可相应地减少．因此基于余数系统的数字信号处理算法可为数据通道设计在高速、低复杂度、低功耗等方面找到平衡点，对现代移动设备、机载和星载设备等有重要意义．模集合的具体形式是决定其超大规模集成电路实现复杂度的主要因素之一，因为模集合的形式决定了各余数通道的基本运算单元——模加法和模乘法的运算复杂程度．目前，大多数数字逻辑运算均基于二进制逻辑，而模2n±1和模2n加法器具有较简单的超大规模集成电路实现结构，因此多数余数系统均基于模2n±1和2n来构建模集合．本文针对模集合{2n,2n-1,2n+1-1,2n-1-1}进行后置转换电路设计．该模集合为3模集合{2n-1, 2n, 2n+1, 2n+1-1, 2n-1-1}中剔除模2n+1得到[1-2]．证明当n为偶数时上述的余数基之间是两两互质的．该模集合整体动态范围利用率接近于1，有较好的并行度和平衡度．本文采用改进后的混合基算法对其后置转换电路进行设计，电路采用简单的流水线实现方式，有利于各模块的优化．

1　混合基后置转换算法

设m1,m2,m3,…,mN是两两互质的正整数，对于给定的一组余数基{m1,m2,m3,…,mN}，混合基后置转换算法有：

X=aNmN-1mN-2…m1+…+a3m2m1+a2m1+a1.

(1)

通常的混合基后置转换算法对aNaN-1…a1的求解效率比较低，文献[3]提出了一种提高并行性的方法．令(x1,x2,x3,…,xN-1,xN)是X在该集合下的模，即xi=(X)mi,则

a1=x1,

(2)

a2=m2(x2-a1),

(3)

a3=m3(m3(x3-a1)-a2)m3,

(4)

…

aN=mNmN{…mN×

(5)

2　电路设计与实现

本文针对模集合{2n,2n-1,2n+1-1,2n-1-1}(n为偶数)设计其后置转换电路．由式(1)可得X=a42n(2n-1)(2n+1-1)+a32n(2n-1)+a22n+a1.

(6)

由式(2)～(5)可得：

a1=x1,

(7)

a2=(2n)-12n-1(x2-a1)2n-1,

(8)

a3=(2n-1)-12n+1-1((2n)-12n+1-1×

(x3-a1)-a2)2n+1-1,

(9)a4=(2n+1-1)-12n-1-1((2n-1)-12n-1-1×

(10)

除式(7)外，式(8)～(10)均包含了乘法逆元项，计算可得各乘法逆元:

(2n)-12n-1=1,

(11)

(2n)-12n+1-1=2,

(12)

(2n-1)-12n+1-1=-2,

(13)

(2n)-12n-1-1=2n-2,

(14)

(2n-1)-12n-1-1=1,

(15)

.

(16)

当n为偶数时，式(16)中(2n-1)/3是一个正整数，有

(17)

将式(11)～(17)中的各乘法逆元值代入式(8)～(10)可得

a2=x2-x12n-1,

(18)

a3=4(x1-x3)+2a22n+1-1,

(19)

a4=2n-1-1.

(20)

由于x1、x2、x3、x4分别是n位、n位、n+1位、n-1位的二进制数，在二进制数系统下，它们可以表示为：

x1=(x1,n-1x1,n-2…x1,0)2,

x2=(x2,n-1x2,n-2…x2,0)2,

x3=(x3,nx3,n-1…x3,0)2,

x4=(x4,n-2x4,n-3…x4,0)2.

为进一步推导a1、a2、a3、a4在二进制数下的表达式，应用如下运算与引理：

(1)xk(m)表示xk的低m位所表示的二进制数，若xk是小于m位的二进制数，则其多出来的高位补0；

(2)x≪k或x≫k分别表示二进制数x循环左移或右移k位；

引理1在模2n-1运算中，余数v的负数-v可以用v的反码形式表示，其中0≤v≤2n-1,即：

-v2n-1=2n-1.

(21)

引理2在模2n-1运算中，当余数v与权重为2的数2k做模运算时，只需对v做k位的循环左移操作，即

2k·v2n-1=(v≪k)2n-1.

(22)

根据式(21)与式(22)进一步化简式(18)～(20)，得

a2=2n-1，

(23)

a3=2n+1-1，

(24)

a4=

(25)

(26)

则a4=U+(U≪ 2)+(U≪ 4)+…+(U≪n-2)2n-1-1.

(27)

对于n≥5,a2可以通过一个模2n-1加法器来实现．a3的实现结构是一个(3,2n+1-1)MOMA(Multi Operand Mode Adder,多操作数的模加法器),由一个n+1位回旋进位保留加法器与模2n-1加法器实现．图1给出了a2、a3及Y的实现结构．对于a4,先求U，其实现结构是一个(5,2n-1-1)MOMA．求得U后，通过一个(n/2,2n-1-1)MOMA即可得到a4,如图2所示．

图1　a2, a3及Y的硬件实现

最后通过式(6)可得到X=a42n(2n-1)(2n+1-1)+a32n(2n-1)+a22n+x1=

[a4(2n-1)(2n+1-1)+a3(2n-1)+a2]2n+x1=[a4(22n+1-2n-2n+1+1)+a3(2n-1)+a2]2n+x1.

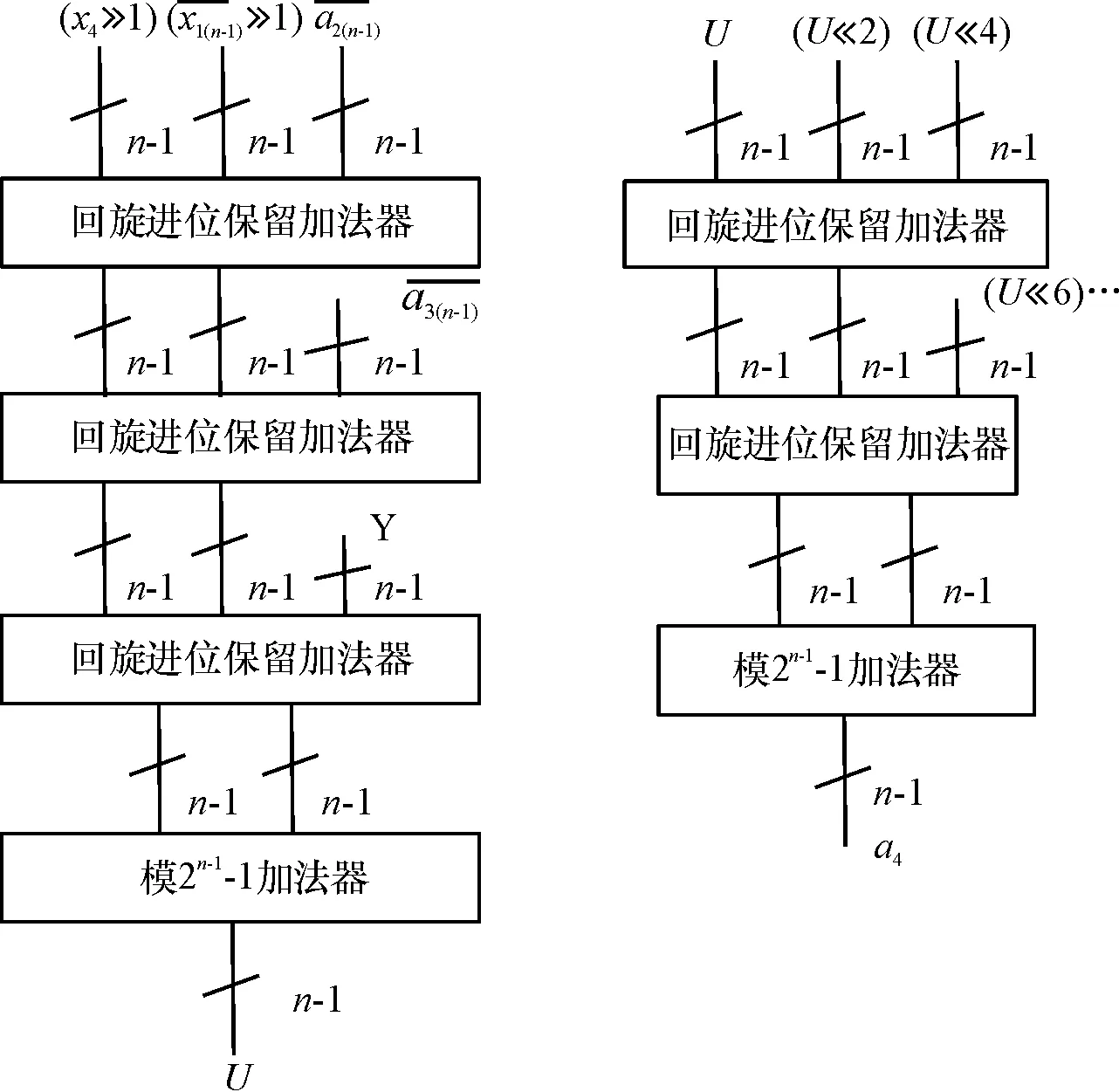
图2　U和a4的硬件实现

由于W1、W2、W3、W4都是3n位的补码表示，所以W的运算只需要一个4输入的3n位补码加法器．该加法器由2级3n位进位保留加法器(CSA)及一个3n位的并行前缀加法器来实现(图3).由于W1、W2、W3、W4分别包含n位的1以及2n+1位的0、2n+1位的1，在图3的2级CSA中，总共有4n+2个FA(全加器)被替换为更节省资源的2n对XNOR/OR门，n+1对XOR/AND门和n个非门,以节省硬件资源．

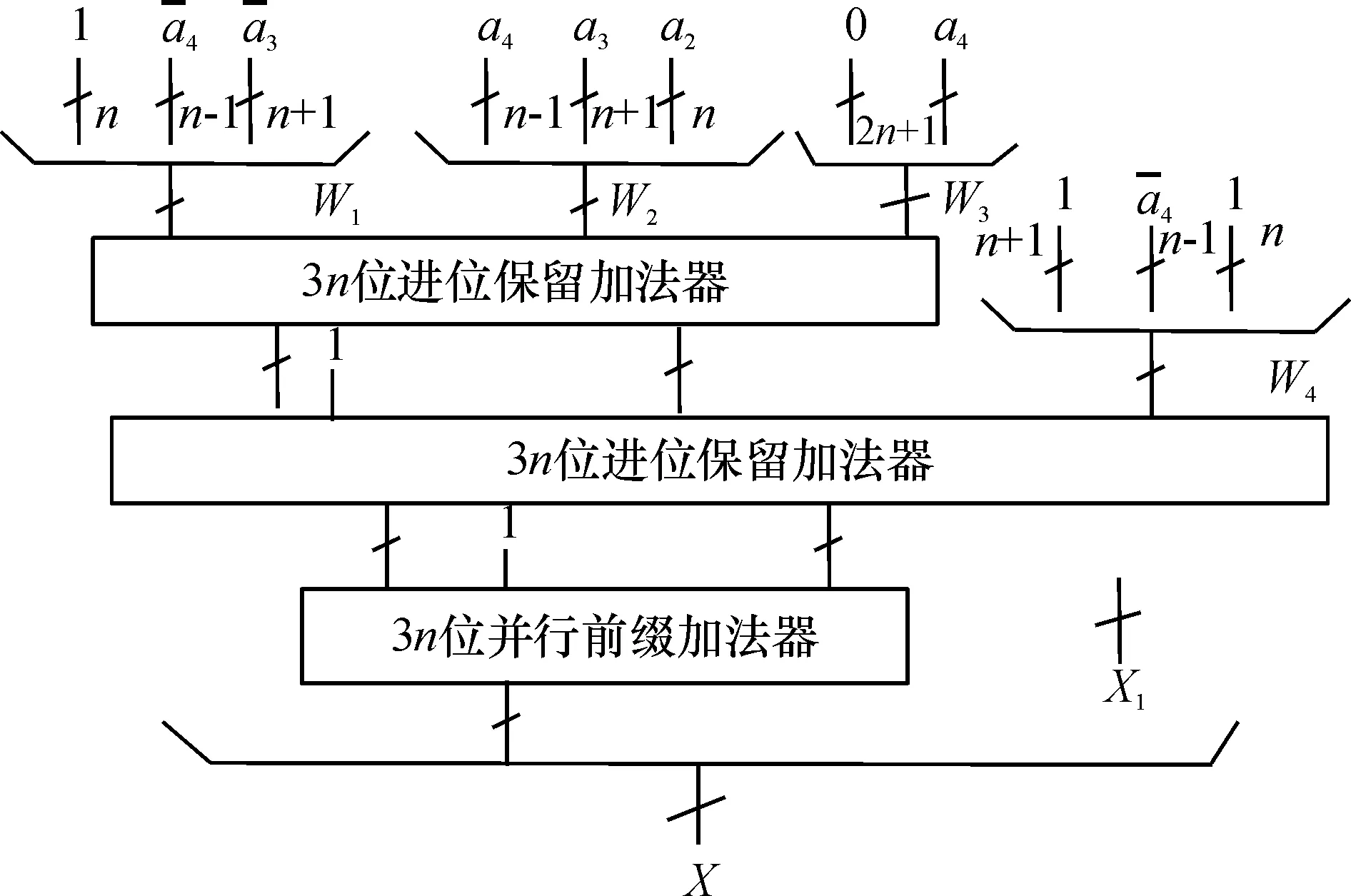
图3　X最终硬件实现模块

上述后置转换电路实现结构都是基于门器件，由门器件构成的重复单元电路多是FA，2输入模加法器及并行前缀加法器．在模2n-1加法器的选择上，采用端回进位前缀结构[3]．虽然基于混合基算法的R/B电路是一种串行算法，但由于本文模集合的特殊形式，电路采用简单的实现方式因而缩短了延时路径．

与近年报道的一些具有近似相同动态范围的模集合后置转换电路相比[4-6]，在n>8时，本文所设计的后置转换电路，其性能有明显的优势．

3　结语

针对模集合为{2n,2n-1,2n+1-1,2n-1-1}的余数系统，采用改进后的混合基算法设计其后置转换电路．该后置转换电路仅由加法器组成的组合逻辑电路来实现，避免了ROM及时序电路的引入，减少了关键路径的延时．

[1]徐明鹤.余数系统后置转换和符号检测电路的设计[D].广州：华南理工大学,2012.

Xu M H.Design on reverse converter and sign detection circuit for residue number system[D].Guangzhou: South China University of Technology,2012.

[2]Cao B, Chang C H, Srikanthan T. A residue-to-binary converter for a new five-moduli set[J]. IEEE Transactions on Circuits and Systems- I, 2007, 54(5): 1041-1049.

[3]胡剑浩，马上.余数系统原理与在高速数字信号处理中的应用[M].北京：科学出版社，2012.

[4]Mohan P V A, Premkumar A B. RNS-to-binary converters for two four-moduli sets {2n-1, 2n, 2n+1, 2n+1-1} and {2n-1, 2n, 2n+1, 2n+1+1}[J]. IEEE Transactions on Circuits and Systems-I, 2007, 54(6): 1245-1254.

[5]Mohan P V A. New reverse converters for the moduli set {2n-3, 2n-1, 2n+1, 2n+3}[J]. Aeu-International Journal of Electronics and Communications, 2008, 62(9): 643-658.

[6]Skavantzos A, Abdallah M, Stouraitis T. Large dynamic range RNS systems and their residue to binary converters[J]. Journal of Circuits Systems and Computers, 2007, 16(2): 267-286.

【中文责编：庄晓琼英文责编：肖菁】

A Circuit Design of Residue to Binary Converter Using the Mixed Radix Algorithm

Huang Shiyang, Chen Fenyi, Yao Ruohe*

(School of Electronic and Information Engineering, South China University of Technology, Guangzhou 510640, China)

The conversion of residue number system to binary system using traditional mixed radix conversion lacks of parallelism. An improved mixed radix conversion is proposed. A residue to binary(R/B) conversion circuits based on moduli {2n,2n-1,2n+1-1,2n-1-1} is studied and designed. The modulo 2n-1 adder has a relatively simple implementation, in which the design of the circuit is to avoid the introduction of read-only memory and time sequence circuit, and the R/B conversion circuit is implemented by a simple combination of logic and adder cascade. The analysis results show that the reverse converter shortens the delay of critical path and decreases the power dissipation efficiently. Compared to those R/B converters with same dynamic range designed in recent years, the circuit designed in this paper has a better performance advantage apparently.

mixed radix conversion； residue number system； modulo adder

2015-01-06《华南师范大学学报(自然科学版)》网址：http://journal.scnu.edu.cn/n

国家自然科学基金项目(61274085);华南理工大学中央高校基本科研学生项目(10561201435)

姚若河，教授，Email:phrhyao@scut.edu.cn.

TP399

A

1000-5463(2015)05-0159-04