一类由两个同型部件与一个修理设备构成的系统研究中出现的投影算子的表达式∗
阿力木米吉提
(新疆广播电视大学新疆乌鲁木齐 830049)
0 引言
可靠性是为适应产品的高可靠要求而发展起来的新兴学科,其中一个重要的研究内容是系统的建模与分析.大量的可靠性问题通过建立相应的数学模型来研究.许多方法可以帮助我们建立可靠性模型,其中比较重要的一个就是补充变量方法.1955年 Cox[1]通过以服务时间作为补充变量建立了M/G/1排队模型并且得到了该排队模型的稳态解的存在性.1963年Gaver[2]首次成功地应用补充变量方法研究了一个可靠性问题.从此以后许多学者利用补充变量方法研究了很多可靠性问题.在文献[3]中作者首先用补充变量方法建立了描述由两个同型部件和一个修理设备构成的系统的数学模型,然后对此模型进行了动态分析:运用泛函分析中的算子半群理论证明了此模型正时间依赖解的存在唯一性,其次当修复率函数µ(x)满足Lipschitz条件时证明了该模型的主算子生成的算子半群是拟紧算子,由此推出了此算子半群指数收敛于某个投影算子.本文在文献[3]的基础上,当修复率为常数时,通过研究该模型研究中出现的的投影算子的表达式得到该模型的时间依赖解指数收敛于其稳态解.
当µ(x)=µ时,由两个同型部件与一个修理设备构成的系统的数学模型可写为(见文献[3])
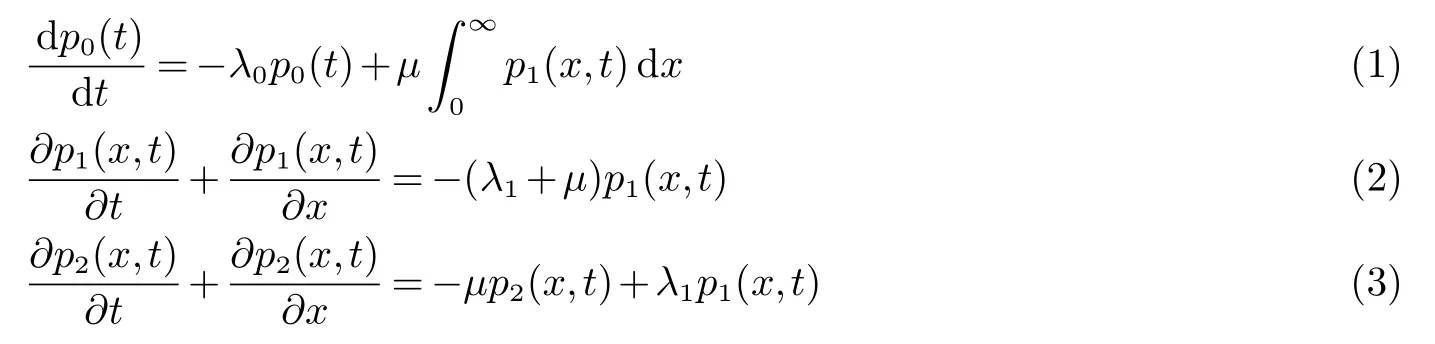

其中(x,t)∈[0,∞)×[0,∞);p0(t)表示在时刻t两个部件都完好的概率;p1(x,t)dx表示在时刻t系统中一个部件故障并且故障部件已消耗的修理时间在(x,x+dx]内的概率;p2(x,t)dx表示在时刻t两个部件都故障并且正在修理的部件已消耗的修理时间在(x,x+dx]内的概率;λ0表示一个部件故障的概率;λ1表示两个部件都故障的概率;µ表示修复率.本文沿用文献[3]中的符号.取状态空间为
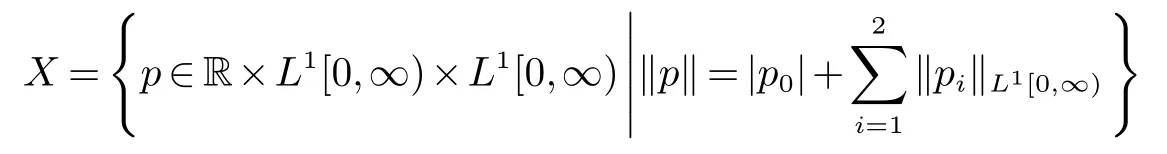
显然X是一个Banach空间.为方便起见,记
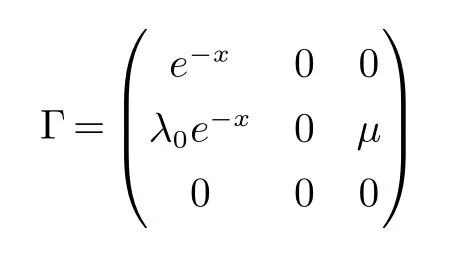
以下定义算子及其定义域
D是绝对连续函数,且
若对p∈D(A)定义
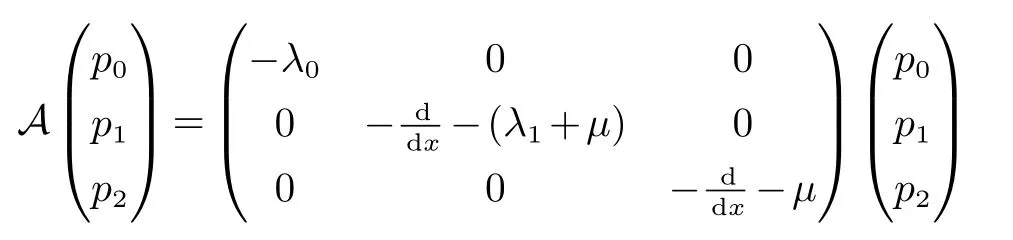
且对p∈X定义
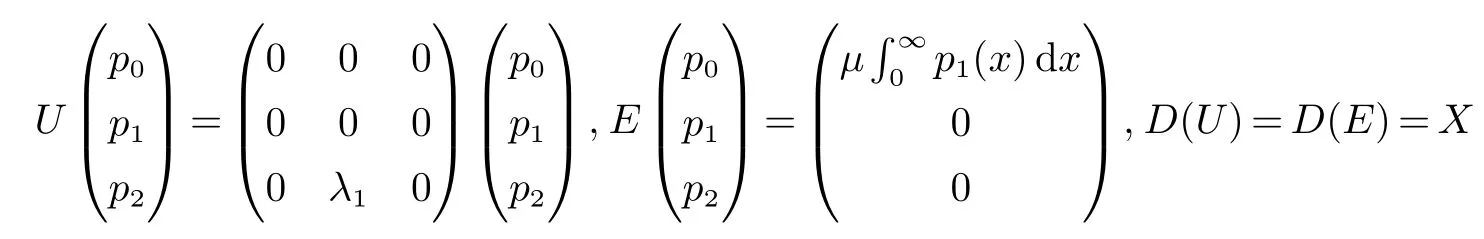
则上面的方程组(1)—(6)可以改写为Banach空间X中的抽象Cauchy问题:

在文献[3]中作者得到了以下结果:
引理1A+U+E的共轭算子(A+U+E)∗为

其中
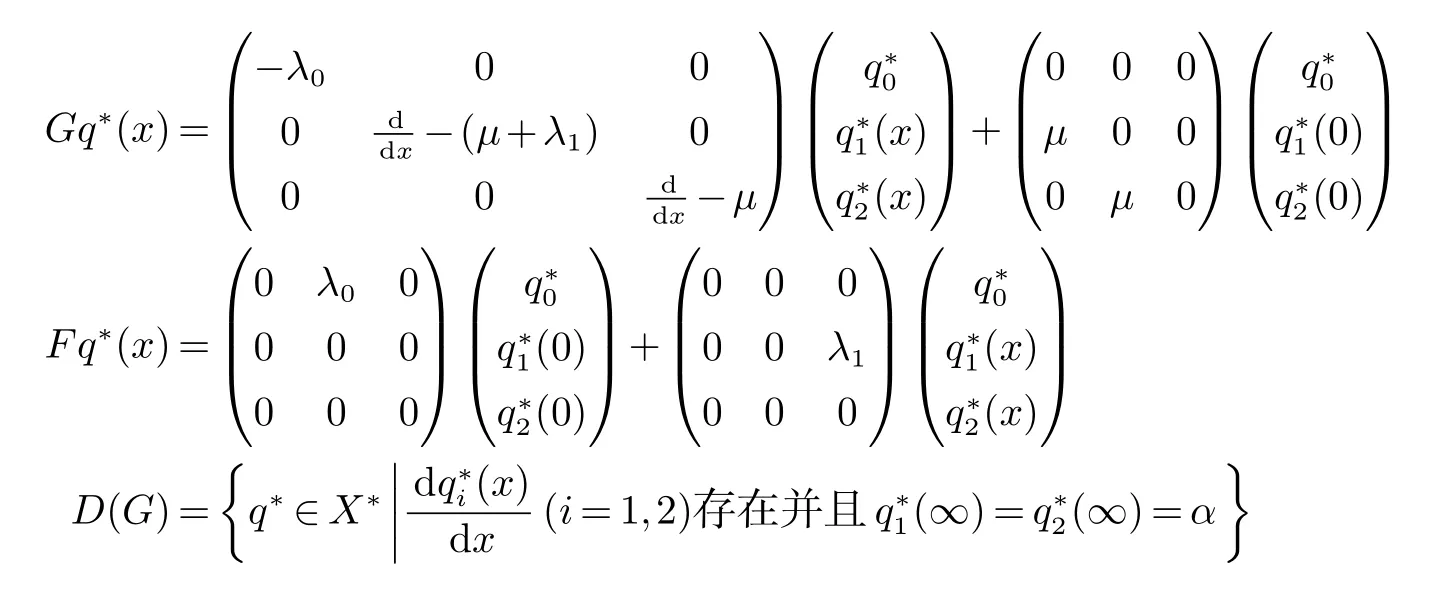
这里

定理1A+U+E生成一个正压缩C0-半群T(t).
定理20是的代数重数为1的特征值.
定理3T(t)是拟紧算子.存在一个正投影算子使得
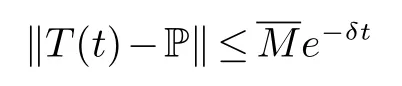
本文研究定理3中P的表达式.首先研究A+U+E在左复平面中的谱,然后结合定理1,定理2,定理3与复变函数中的有关知识得到所要的结果.
1 主要结果
引理2当是A+U+E的几何重数为1的特征值,且在圆内除0外没有其他特征值.
证明讨论方程[γI−(A+U+E)]p=0,即

解(9)与(10)得到
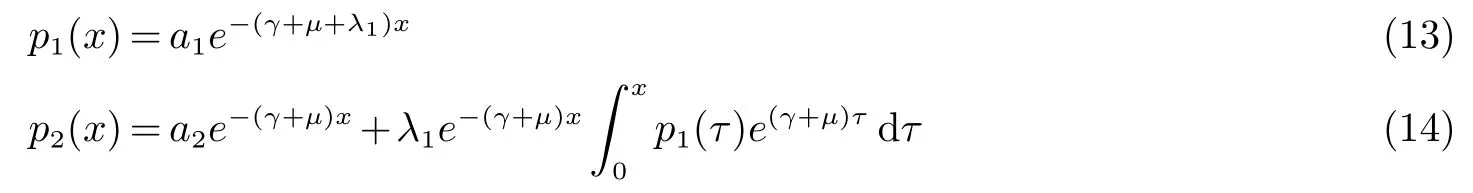
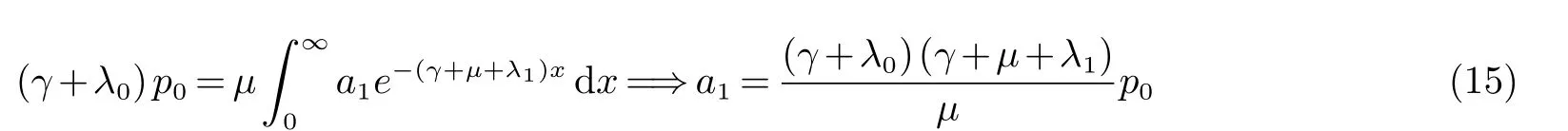
由(12)与(14)知道

将(14)代入(11)式并用关系式a1=p1(0),a2=p2(0)=0和Fubini定理得到


合并(15)和(17)推出

其中γ=0是定理2中的结果,所以我们以下只讨论(19)和(20).由条件µ>λ0知道

将(19)代入(15)算出
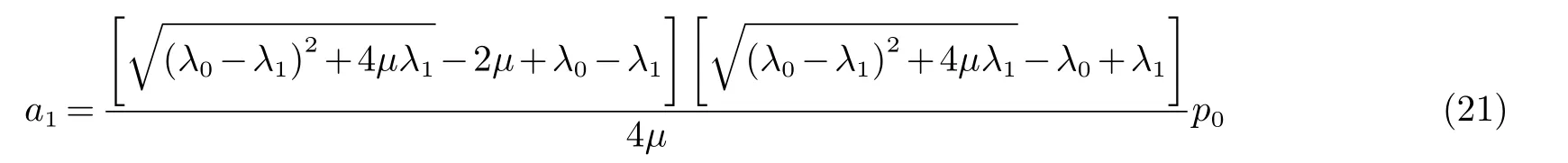
由(13),(14),(15),(16),(19),(21)与Fubini定理得到
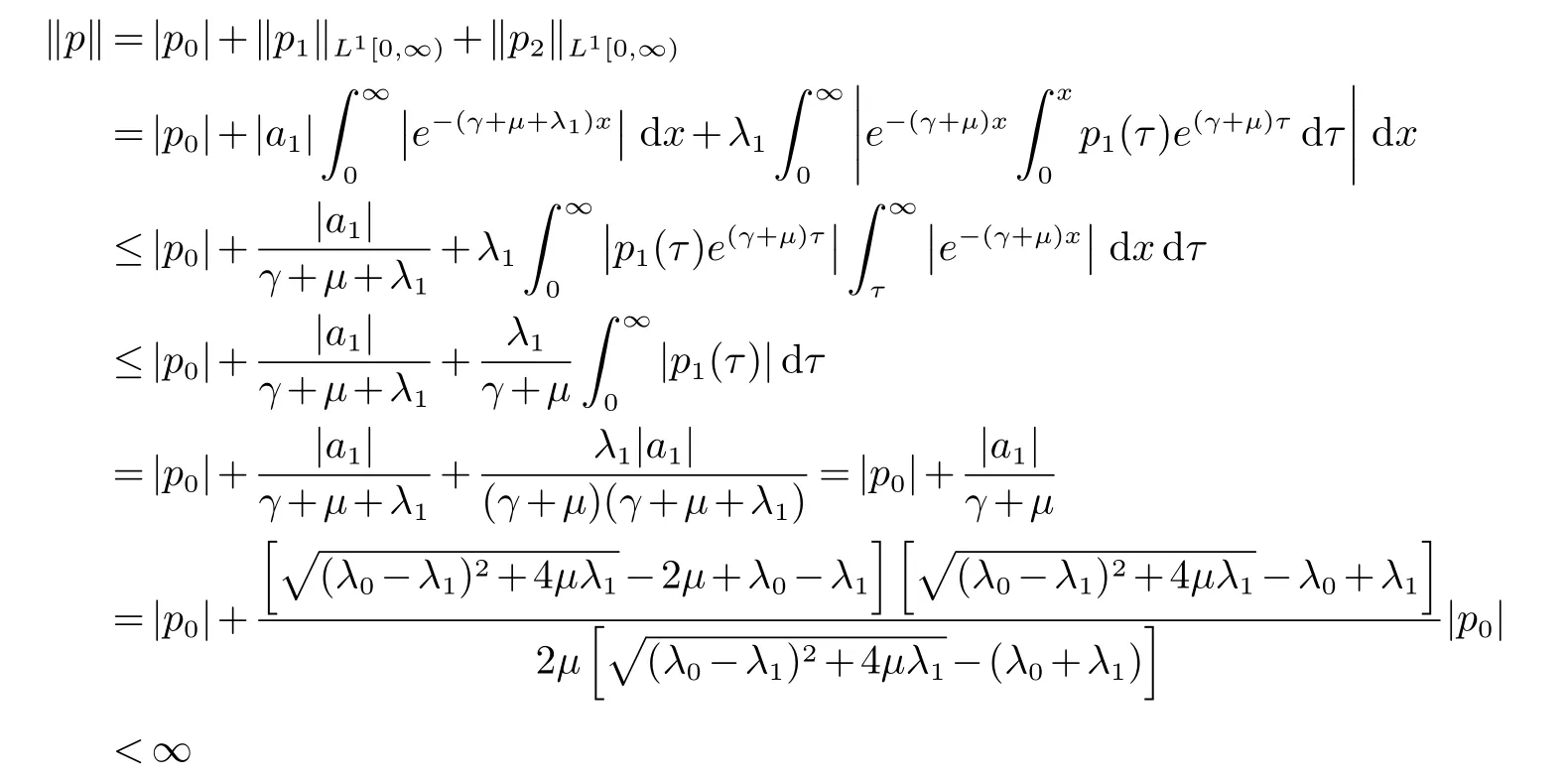
由(13),(14),(15),(16),(20)并用Fubini定理推出
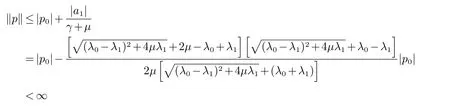

内除0外没有其他特征值.
引理3当µ>λ0>0时,是(A+U+E)∗的几何重数为1的特征值,且在圆内除0外没有其他特征值.
证明讨论方程[γI−(A+U+E)∗]q∗=0,根据引理1该方程等价于
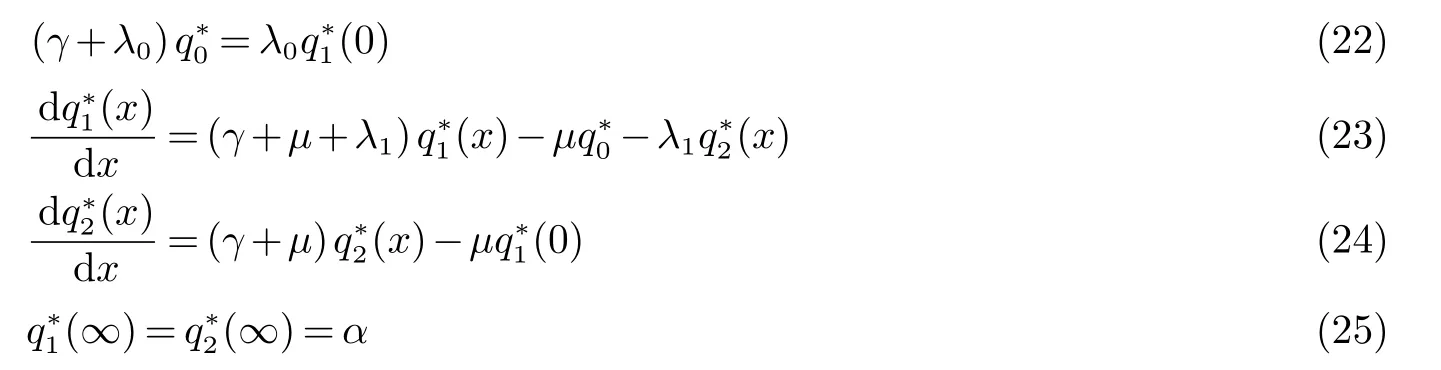
解(22)-(24)得到(不妨设Reγ+µ>0)
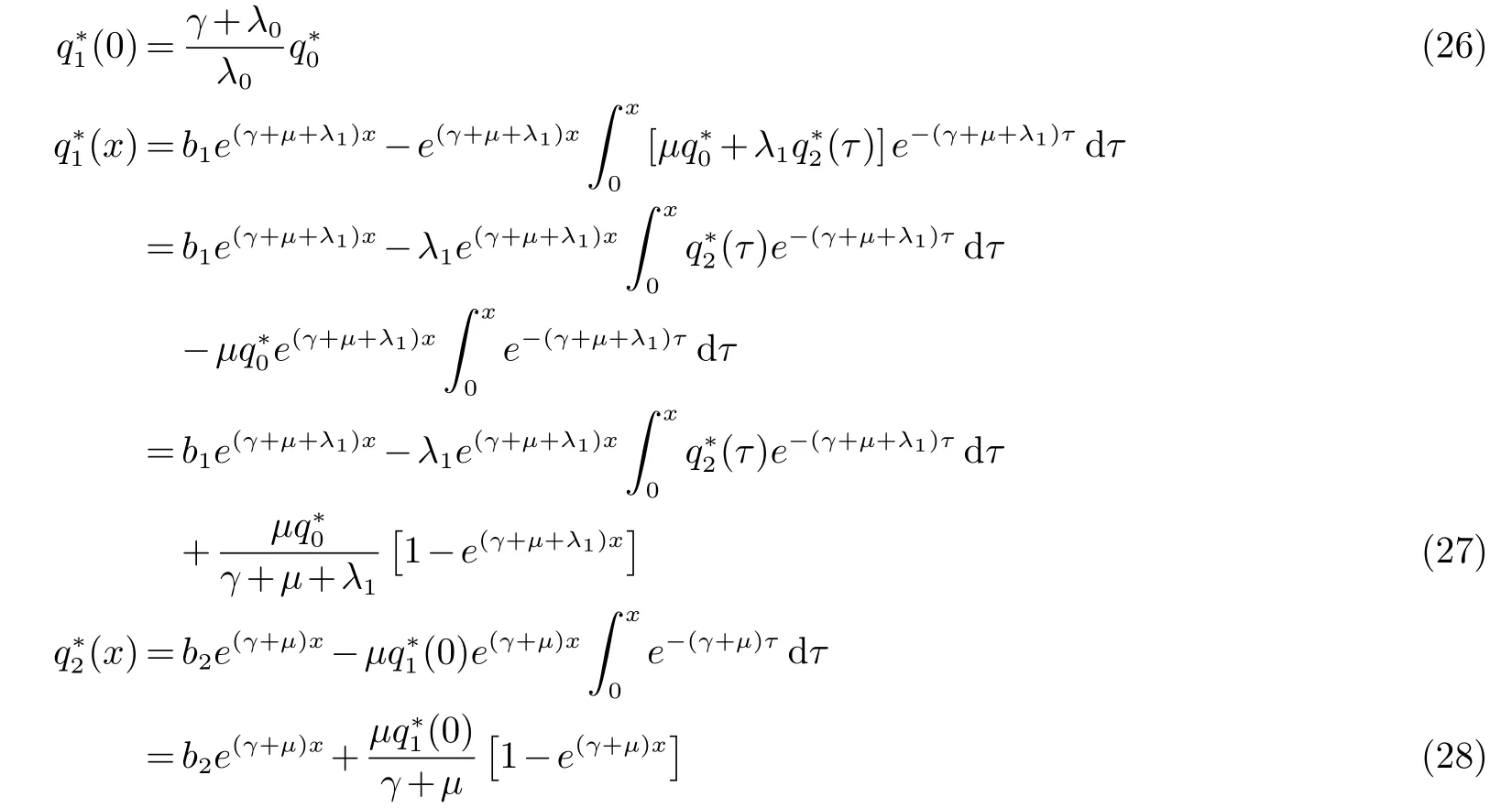
(27) 式两边乘e−(γ+µ+λ1)x,(28) 式两边乘e−(γ+µ)x,令x→∞并用 (25) 算出
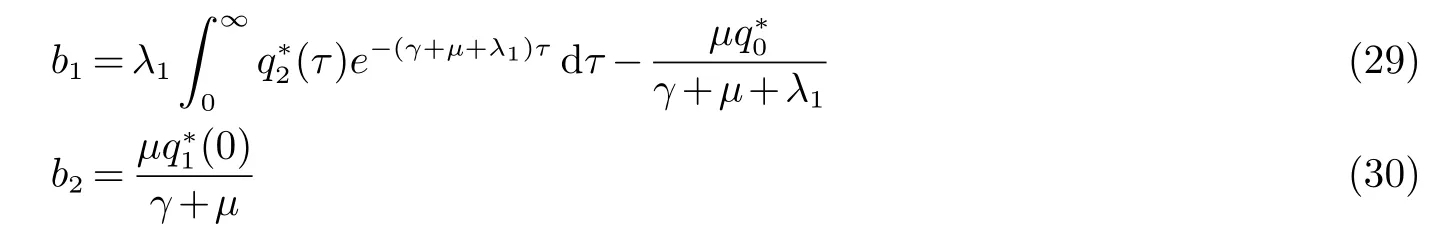
将(29)代到(27),(30)代到(28)推出

由(32)与(26)知道
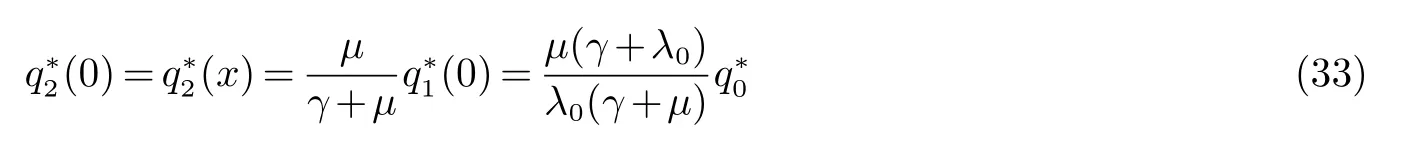
将(33)代入(31)有

由(34)与(26)算出

其中γ=0是定理2中的结果,所以以下只讨论(36)和(37).由条件µ>λ0知道

将(36)代入(26),(33)推出
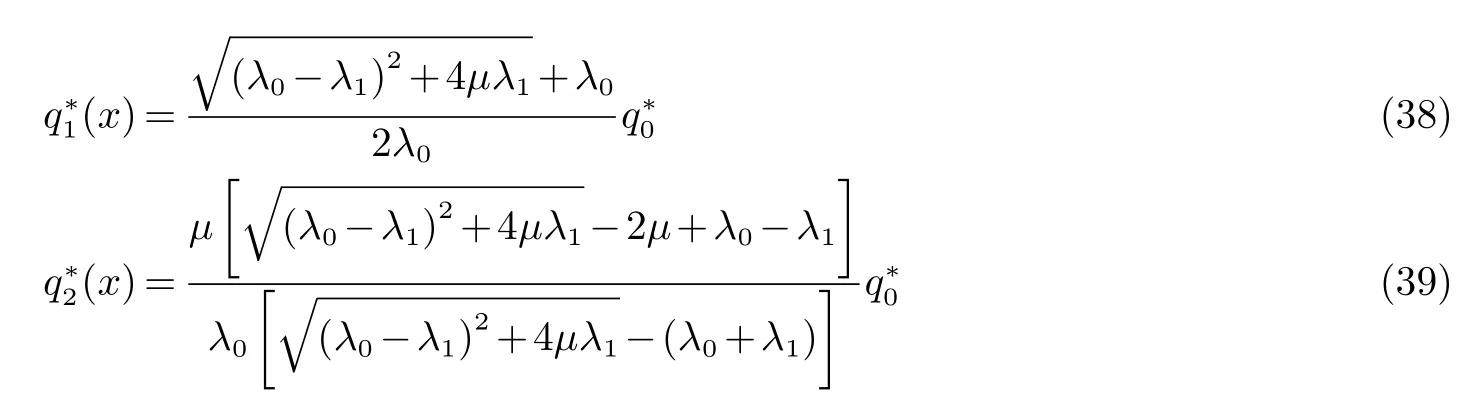
(38)与(39)表示

由(26),(33)与(37)推出
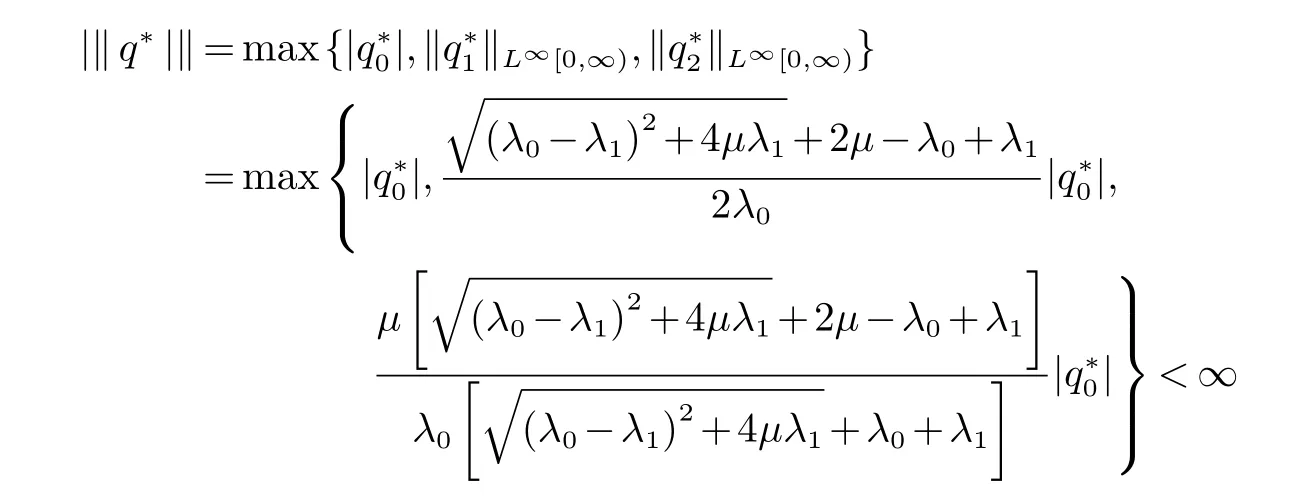
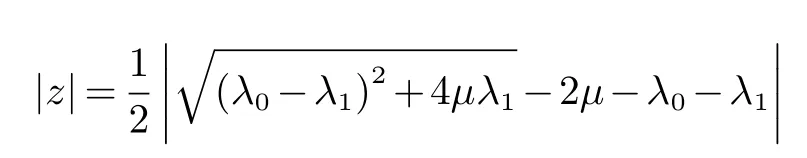
内除0外没有其他特征值.
引理4当有

这里
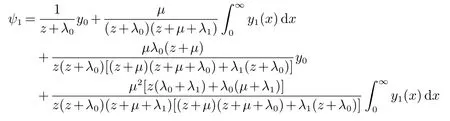

证明对即
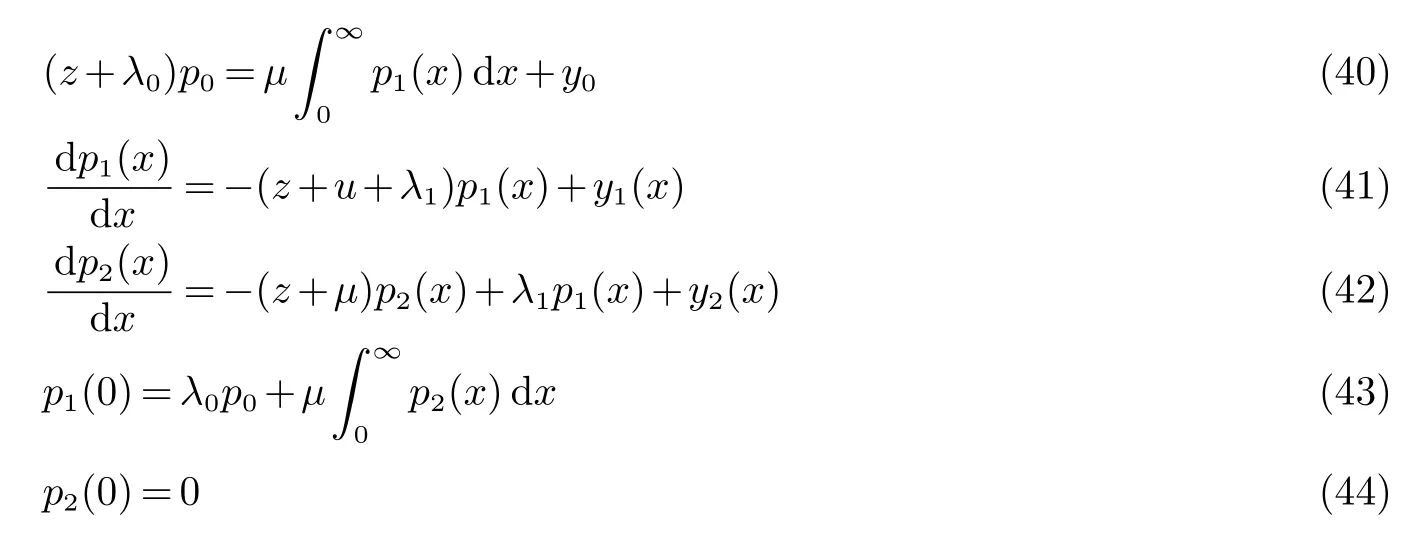
解(40)-(42)有
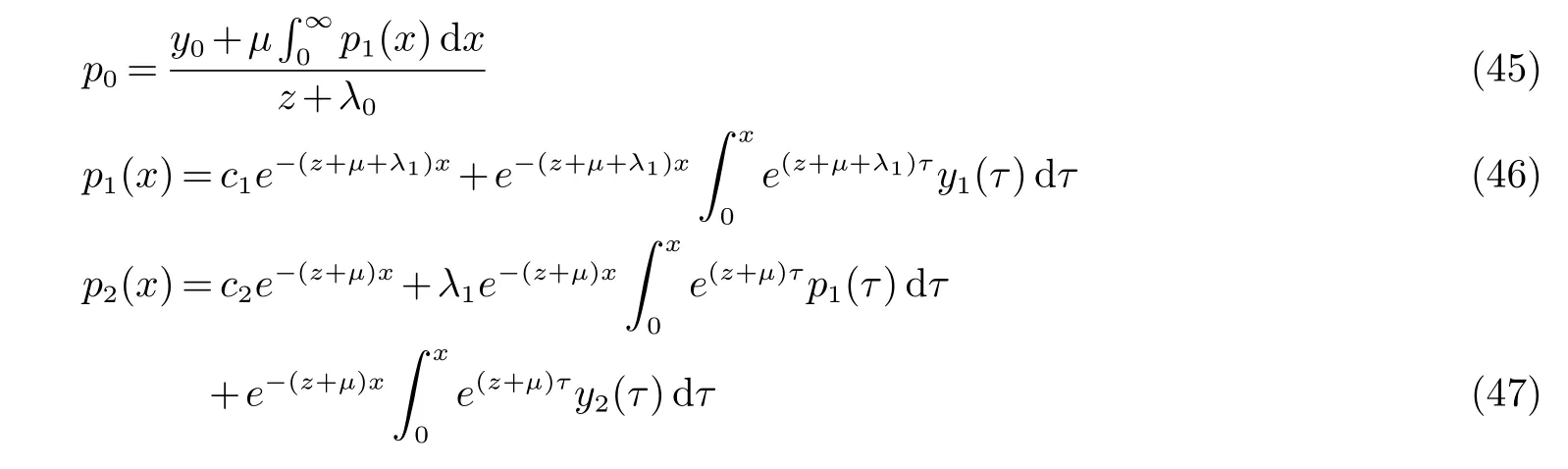
合并(45),(46),(47)并用关系式c1=p1(0),c2=p2(0)=0和Fubini定理计算出(不妨设Rez+µ>0)


下面求p1(0).将(48),(50)代入(43),并用Fubini定理得到(不妨设Rez+µ>0)


将(51)代入(48),(49),(50)得到此引理的结论.
引理5当µ>λ0>0时,对∀y∈X,定理3中的投影算子P的表达式为

其中
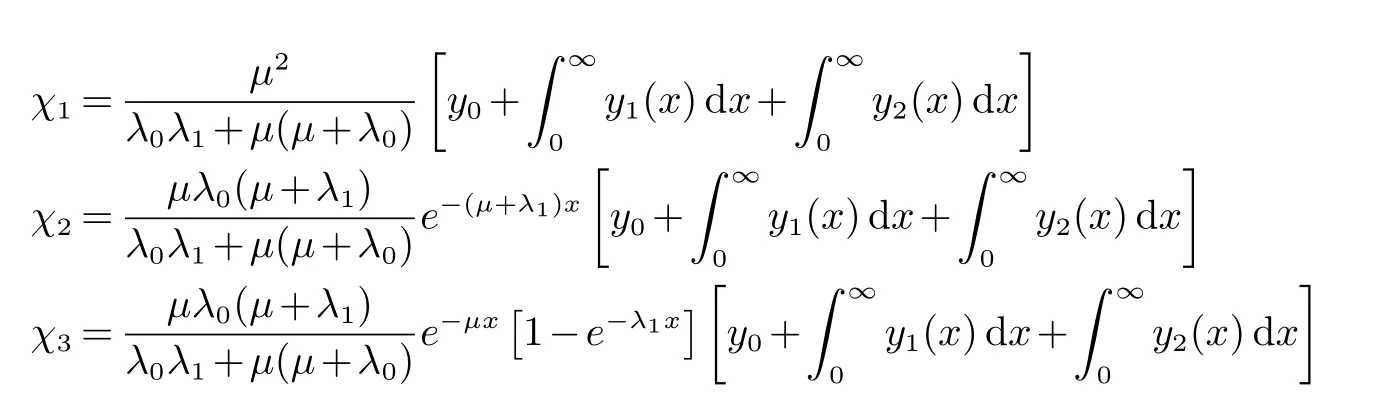
特别地对初值p(0)=(1,0,0)有
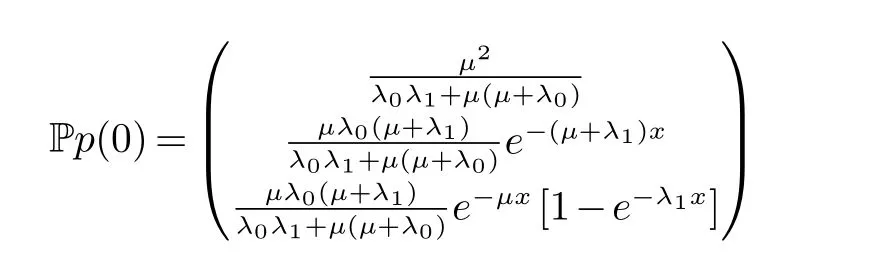
其中p(x)是系统(7)的稳态解(见文献[3]).
证明由定理2,定理3,引理2及引理3知道,在圆
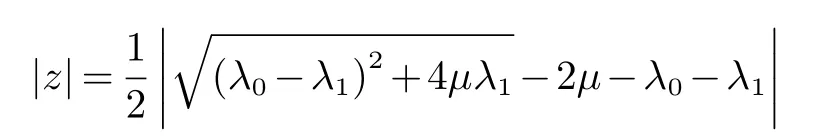
内除0外其它点都是A+U+E的正则点.由此推出z=0是(zI−A−U−E)−1的一级极点,从而由留数定理[4]与引理4知道对∀y∈X有
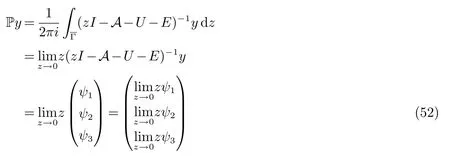
由ψi的定义(见引理4)推出

特别地,对初值p(0)=(1,0,0)有

将(53)-(55)与(56)-(58)代到(52)得到此引理的结论.
结合定理1,定理3,引理5得到
定理4当µ>λ0>0时,系统(7)的时间依赖解指数收敛于该系统的稳态解,即存在正数使得
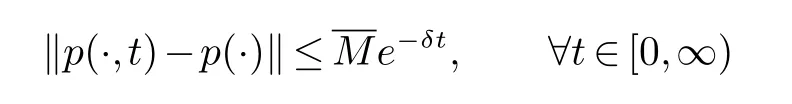
其中p(x,t)是系统的时间依赖解,p(x)是系统的稳态解.
证明由定理1知道系统(7)存在唯一的正时间依赖解p(x,t),并把它可表示为

由引理5知道

从而由定理3,(59),(60)推出
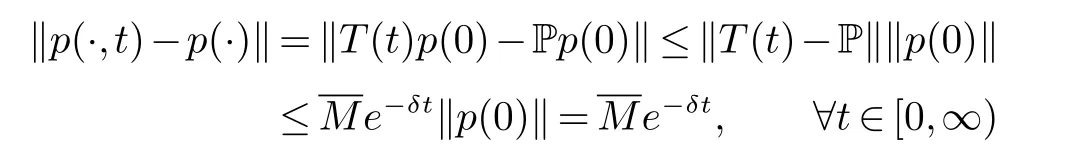
- 新疆大学学报(自然科学版)(中英文)的其它文章
- Spin-filtered Edge States and Quantum Spin Hall Effect in Bilayer Graphene∗
- WSNs中基于Chebyshev多项式的可认证密钥协商方案∗
- 新疆双峰驼乳清蛋白组分对人宫颈癌HeLa细胞增殖的抑制作用∗
- 新疆加曼特金矿与斑岩型金矿的对比研究∗
- 具有非倍测度的参数型Marcinkiewicz积分交换子在Hardy空间的估计∗
- Periodic Solution of a Two-species Competitive Model with State-Dependent Impulsive Replenish the Endangered Species∗

