Spin-filtered Edge States and Quantum Spin Hall Effect in Bilayer Graphene∗
XU Lei,ZHANG Jun,2,†
(1.College of Physics Science and Technology,Xinjiang University,Urumqi Xinjiang 830046,China;2.State Key Laboratory of Theoretical Physics,Institute of Theoretical Physics,Chinese Academy of Sciences,Beijing 100190,China)
Abstract: We report the investigation of topological phases in biased bilayer graphene at a magnetic field.Various kinds of topological phases can be obtained when considering the intrinsic spin-orbit coupling.Topological phase transition between these phases can be realized by tuning the bias voltage and Fermi energy.Besides,the stability of time-reversal symmetry-broken quantum spin Hall effect is investigated,which is robust against symmetry-breaking perturbations.The combined effect of intrinsic SOC and Zeeman splitting is also explored,and we find that the QSH phase is broken by a large Zeeman splitting whereas the spin-filtered QH phase remains.These results could have great potential for applications in spintronics devices.
Key words:topological phase;intrinsic spin-orbit coupling;bilayer graphene
0 Introduction
Graphene has attracted intense research interests for both fundamental physics and potential nanoelectronic device applications[1−3].Graphene exhibits an unique linear energy dispersion and particle-hole symmetry near the Dirac cones,which results in a novel quantum Hall(QH)effect and high carrier mobility[4,5].The QH effect can be characterized by chiral spin-degenerate edge states.Moreover,graphene has also been suggested to be a two-dimensional quantum spin Hall(QSH)system[6,7],which is characterized by helical edge states formed by counterpropagating edge states with opposite spins.Bilayer graphene also exhibits remarkable phenomena.The low-energy excitation in bilayer graphene is no longer linear but quadratic[8],which leads to an unusual integer QH effect[8,9],owing to spin and valley degeneracy[9].Also,a controllable and tunable energy gap may open,which can be tuned by an external gate voltage[9−12]or via a chemical doping[13].This has many potential device applications[14].In addition,the Rashba spinorbit coupling(SOC)in bilayer graphene can open a bulk energy gap and the system can host an unconventional QSH effect[15].
It is known that SOC-induced QSH effect is protected by time-reversal symmetry(TRS)and can be described by aZ2topological invariant[7,16,17].However,SOC is proved to produce an unobservable effect under realistic conditions in graphene[18,19],so that it is often neglected in many works.Fortunately,SOC has been recently predicted to enhance dramatically by depositing heavy adatoms,which produces a sizable QSH gap[20,21].Furthermore,two kinds of TRS-broken QSH effects have been theoretically predicted in graphene so far[7,16,17].One is induced by the intrinsic SOC combined with an exchange field[22]or a magnetic field[23,24].The other isCT-invariant QSH effect in ferromagnetic graphene with a magnetic field[25],whereCis the charge conjugation operation andTis the time-reversal operation.
Motivated by these developments,in this work,we investigate topological phases in biased bilayer graphene at a magnetic field.When taking the intrinsic SOC into account,weak QSH,QSH and spin-filtered QH phases can be revealed and we find that TRS-broken QSH phase is robust against symmetry-breaking perturbations.The tunability of topological phases is also addressed.In addition,we explore the combined effect of intrinsic SOC and Zeeman splitting,and find that the QSH phase can be destroyed by a large Zeeman splitting,whereas the spin-filtered QH phase remains.The practical feasibility of these results are also proposed,which may open a way for developing novel spintronics devices.
1 Model and method
The tight-binding model of monolayer graphene in the presence of both intrinsic SOC and uniform perpendicular magnetic fieldB=(0,0,−B)is given by[6,7]

where the first term describes hopping between two nearest-neighbor sitesiandjon the honeycomb lattice,tis the hopping amplitude andis the electron creation(annihilation)operator on siteiwith spin α.The Peierls phase due to the magnetic field is given bywith the integral over a line between sitesjandi.The gauge potentialAcan employ Landau gaugeA=(0,−Bx,0)andThe second term is the intrinsic SOC term involving all next-nearest neighbors with coupling strength λS O,and νij=1(−1)if the electron makes a left(right)turn to get to the second bond.szis the spin Pauli matrix.
The Hamiltonian of Bernal-stacked bilayer graphene in the presence of antisymmetric interlayer bias voltage as shown in Fig1(a),takes the form[15]

whereare the top(T)and bottom(B)layer Hamiltonians of Eq.(1),t⊥(takingt⊥=0.13thereafter)is the interlayer hopping between Bernal-stacked neighbors,and 2Uis the bias voltage between the layers and can be controlled and tuned by doping or by adjusting the gate voltage.
In order to discuss the topological property of band structure,we introduce the topological Chern number.For graphene,the topological Chern number[26]and spin Chern number[27]are defined asCc=C++C−andCs=(C+−C−)/2,whereC±is the Chern number for spin-up and spin-down sectors and can be expressed aswith η the valley index[28].In the present model,the spinszis conserved,the spin Chern number andZ2topological index[27,29]yield equivalent descriptions.However,the spin Chern number other thanZ2invariance retains its robustness when TRS is broken.
2 Numerical results and analysis
In this section,we analyze various topological phases induced by the terms in Eq.(2).Before elaborating each topological phase,let us start by recalling the band structure of biased bilayer graphene at a perpendicular magnetic field.The band structure of bilayer graphene at a uniform perpendicular magnetic field can be numerically obtained by diagonalizing the Hamiltonian Eq.(2).It is well known that there is no band gap at zero energy for unbiased bilayer graphene[2].Once applying a bias voltageUacross the layers to break the inversion symmetry in the out-of-plane direction,a band gap∆S O=2Ucan be opened[10].Moreover,an intervalley gap∆Kis opened at a large magnetic field.The gapped energy spectra atU=0.05tfor φ =1/1000 and φ =1/360 are shown in Figs 1(b)and 1(c)as examples.The bias voltage induced intervalley gap is necessary for spin-filtered QH phase,and thus we take φ=1/360 hereafter.The present results are obtained based on zigzag-edged bilayer graphene ribbons and indeed,the same results can be acquired for both zigzag and armchair edge geometries.So we only focus on the bilayer graphene ribbon with zigzag termination in this manuscript.
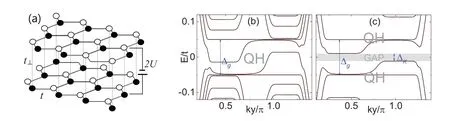
Fig1 (a)Schematic illustration of the lattice structure of bilayer graphene and parameters of our model(see text).Low-energy spectra of zigzag-edged bilayer graphene ribbons for the model with λS O=0 and U=0.05t for(b)φ=1/1000 and(a)φ=1/360.The energy spectra for spin-up and spin-down components are completely degenerate

Fig2 Band structures of zigzag-edged bilayer graphene ribbon at φ =1/360,λS O=0.005t for(a)U=0t and(b)U=0.07t.The black and red curves represent spin-up and spin-down states.(c)-(e)The schematic illustrations of edge state propagation(the direction indicated by arrows)for the weak-QSH,QSH and spin-filtered QH phases,corresponding to the edge states intersected by lines and labeled by the letters in(a)and(b),respectively.“◦”(“•”)means the charge carrier is hole(electron)
The topological phases in unbiased or biased bilayer graphene case have been detailedly discussed in previous works.Now let us extend this study to the intrinsic SOC scheme that does not involve spin flips.The deposition of heavy adatoms can greatly boost the intrinsic SOC,which induces a giant QSH gap about 20.7 meV[20]and 0.2 eV[21].Therefore,the intrinsic SOC induced QSH effect is expected in experiments.We calculate the band structure at a fixed intrinsic SOC λS Ofor different bias voltagesU,and investigate topological phases by varying the Fermi energy.The first insight is given by the low-energy spectra of bilayer graphene ribbon at a fixed intrinsic SOC λS O=0.005t.WhenU=0,the intrinsic SOC opens a bulk gapIn this case,it is easily summarized that for Fermi energy inside the gap|EF|<∆S O[the gray region in Fig2(a)],the system is in the weak QSH phase in Fig2(c),whereas for|EF|>∆S O,the system is in the QH phase.Therefore,one only needs to change the Fermi energy to modulate the topological phase transition.The weak QSH phase in the vicinity of zero energy is characterized by two pairs of helical edge states at each boundary of the system[Fig2(c)].The helical edge states are formed by counterpropagating edge states with opposite spins.The helical edge states are spin-filtered with spin Chern numberCs=2[Fig3(b)],yielding a quantized spin Hall conductance σs=4e/4π.In this case,the backscattering between the modes with opposite spins at the same edge is not forbidden[30],in contrast to the case for monolayer graphene[25].This weak QSH phase can be destroyed by magnetic disorder.
With the increase of applied bias voltageU,the gap∆S Odisappears accompanied by the vanishment of weak QSH,and then opens a new gapIn this gap,new topological phase–the QSH phase and spin-filtered QH phase emerge,in contrast to the case for bilayer graphene without magnetic field,where the system becomes a conventional insulator with vanishing Hall and spin Hall conductances forHere we takeas an example,as shown in Fig2(b).
When Fermi energy is located between the spin-up and spin-down Dirac points,a QSH statewith one pair of edge states at each boundary as sketched in Fig2(d),appears nearby the zero energy in Fig2(b).It suggests that the system be in the QSH phase.It is pointed out that the QSH phase breaks TRS and comes from the combined effect of intrinsic SOC and bias voltage.The QSH phase is protected byCTinvariance in analogy with the ferromagnetic graphene case[25].Here,the spin Chern number isCs=1,giving a quantized spin Hall conductance σs=2e/4π.Due toCTinvariance,the QSH phase is robust against disorder and impurity scattering,and the corresponding spin Hall plateau is very stable.In addition,combining intrinsic SOC with bias voltage,the spin degeneracy is lifted.Hence,Landau levels of the QH phase for each spin sector are separated,and eventually it generates a spin-filtered QH phase.In Fig2(b),when the Fermi energy lies in the intervalley gap∆Kcreated by the bias voltage for any spin species[see the blue dashed line in Fig2(b)],the edge states become spin-filtered leading to a spin-filtered QH effect,as depicted in Fig2(e).The spin-filtered QH state carries both spin current(Cs=1/2)and charge current(C=1)but with a single spin species,resulting in a quantized spin(charge)Hall conductance σs=e/4π (σc=e2/h).This spin-filtered QH phase exists with a nonzero gap
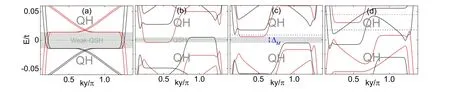
Fig3 Energy spectra of zigzag-edged bilayer graphene ribbon at φ =1/360,λS O=0.005t for(a)U=0 and M=0.04t;(b)U=0.07t and M=0.005t;(c)U=0.07t and M=0.01t;and(d)U=0.07t and M=0.04t.The black and red curves represent spin-up and spin-down states
In the system with a magnetic field,the Zeeman splitting is turned on and takes the formwith effective Zeeman splittingM.It arises a Zeeman-induced gap∆Minstead of the spin-orbit gap∆S O.Thus,the weak QSH phase can persist in the gap created by intrinsic SOC or Zeeman splitting[see Figs 2(a)and 3(a)].Remarkably,the weak QSH phase can be produced by both intrinsic SOC and Zeeman splitting,which highlights the great similarity between Zeeman effect and intrinsic SOC effect.Unlike the above weak QSH case,the Zeeman splitting can break the QSH phase and generates a QH phase instead.To demonstrate this,we calculate the band structure at a fixed bias voltageUand intrinsic SOC λS Ofor different Zeeman splittingsM.By gradually varying the Zeeman splitting,the QSH phase near zero energy disappears,and a gap∆Mopens and then vanishes,as shown in Figs 3(b)-3(d).However,a spin-filtered QH phase can persist in the intervalley gap.
Besides,adjusting the Fermi energy to the value labeled by the pink dashed line in Fig3(d),we can find a spinimbalance QH state at nonzero energy.The spin-imbalance QH state has a very interesting feature that the number of edge modes for each spin sector is not equal.This leads to the edge states carrying both spin and charge currents.For example,the spin(charge)Hall conductance of the spin-imbalance QH state is σs=e/4π (σc=3e2/h)in Fig3(d).Obviously,a spin-filtered QH state is a special instance of spin-imbalance QH state,but with one of the spin components absence.
In general,these topological phases can exist individually or collectively in the system,depending on the filling factors of the two kinds of spin carriers.Tuning the bias voltage will change the topological nature of the gaps,so that the topological phase transition can be realized by varying the bias voltage and Fermi energy.Similarly,at a fixed bias voltage,all these topological phases can be achieved by varying the intrinsic SOC and Zeeman splitting.Note that the Zeeman splitting induced by an external magnetic field is very small,however,the Zeeman splitting in bilayer graphene can be enhanced and tuned individually[31],due to the strong spontaneous spin polarization produced by electron-electron interactions[12,31,32]or via depositing bilayer graphene on a ferromagnetic insulating substrate.Furthermore,the topological phase transition among these phases,corresponding to the transition between chiral state and helical state,may involve rich physics not envisaged up to now.
3 Conclusion
We present a systematic study of the topological phases in biased bilayer graphene at a magnetic field.In the presence of intrinsic SOC,a rich variety of topological phases can be obtained.By tuning the bias voltage,the band structure is changed,and therefore a series of topological phase transitions between different topological Chern numbers are expected to occur.This opens up the possibility to manipulate the transport properties of the system.Interestingly,the TRS-broken QSH phase is robust against symmetry-breaking perturbations.In particular,we explore the combined effect of intrinsic SOC and Zeeman splitting,and the system also exhibits numerous topological phases where the QSH phase is broken but the spin-filtered QH phase is preserved.The experimental observation of these topological phases is expectable in bilayer graphene,and it could be helpful and useful in quantum spin manipulation.
- 新疆大学学报(自然科学版)(中英文)的其它文章
- WSNs中基于Chebyshev多项式的可认证密钥协商方案∗
- 新疆双峰驼乳清蛋白组分对人宫颈癌HeLa细胞增殖的抑制作用∗
- 新疆加曼特金矿与斑岩型金矿的对比研究∗
- 具有非倍测度的参数型Marcinkiewicz积分交换子在Hardy空间的估计∗
- Periodic Solution of a Two-species Competitive Model with State-Dependent Impulsive Replenish the Endangered Species∗
- Permanence and Extinction for Nonautonomous SIRS Epidemic Model with Density Dependence∗

