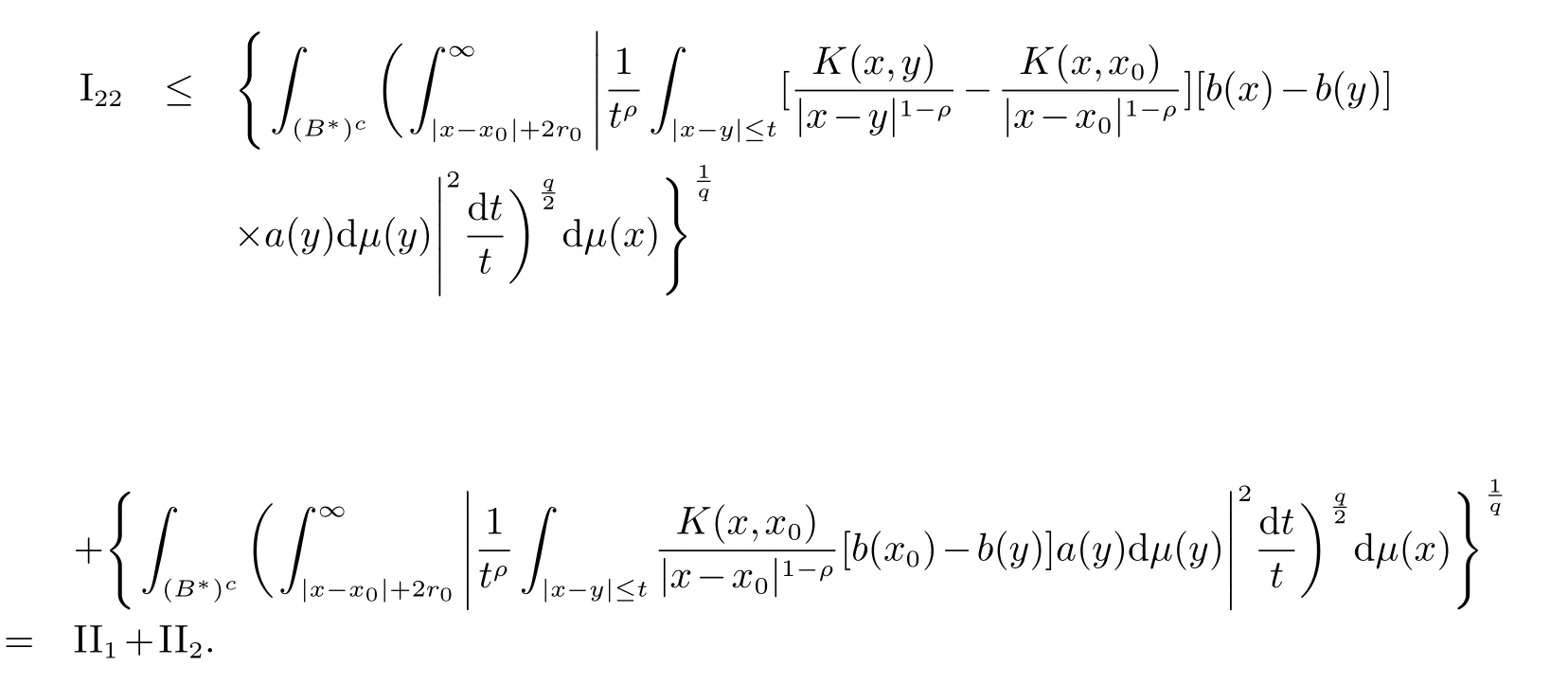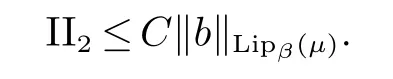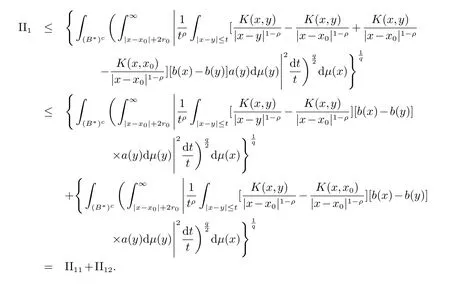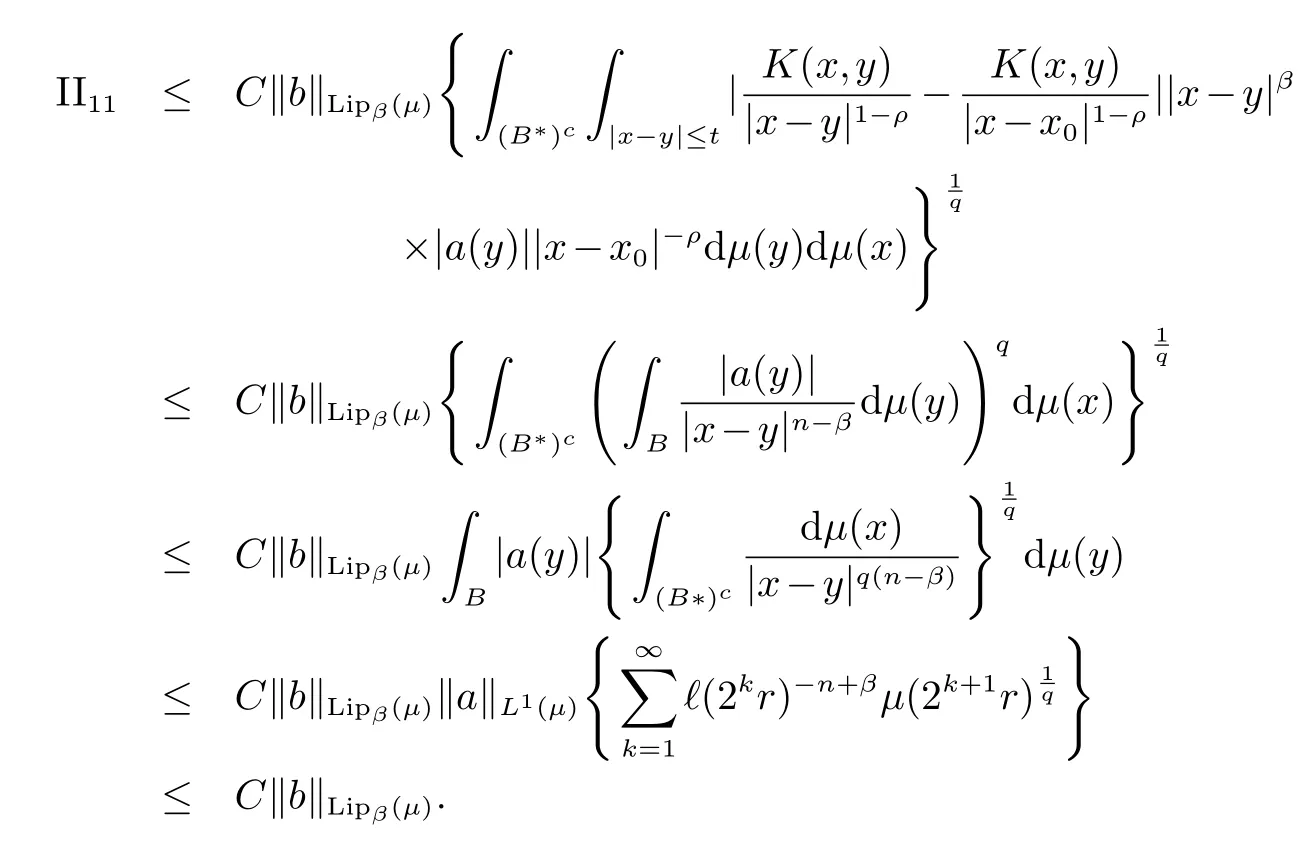具有非倍测度的参数型Marcinkiewicz积分交换子在Hardy空间的估计∗
程 纪,逯光辉,周 疆
(新疆大学 数学与系统科学学院,新疆 乌鲁木齐830046)
0 引言
设µ是定义在上的正Radon测度且满足下面的增长条件:对于所有的都有

其中C0,n是正数且0
设K(x,y)是定义在上的局部可积函数且满足下列条件:存在常数C>0,使得对所有的

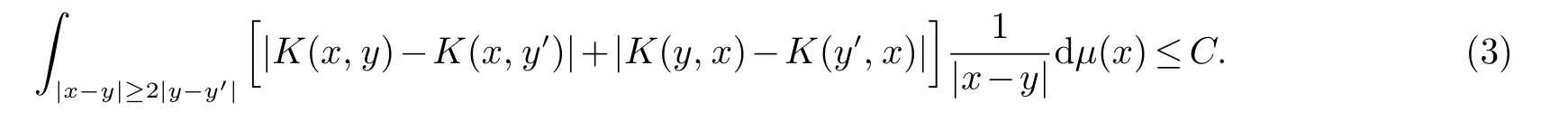
定义关于上述K(x,y)的参数型Marcinkiewicz积分算子为
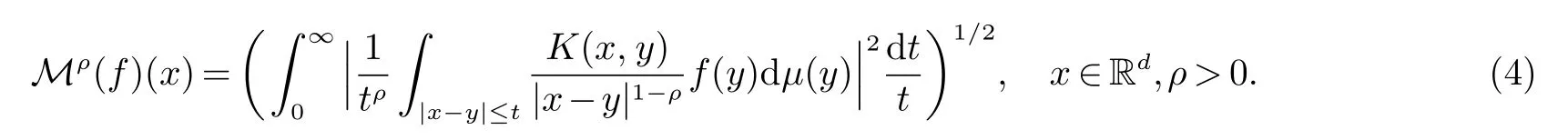
本文假定Mρ(f)(x)(以下都简记为Mρ)在L2(µ)有界.当时, 其中Ω为零次齐次函数则容易验证此K(x,y)满足(2)和(3).又若µ是中的d-维Lebesgue测度.当ρ=1时,则(4)式定义的Mρ恰为Stein引入的标准的Marcinkiewicz积分算子[6].
定义1如果函数满足下列条件

则称f∈Lipβ(0<β<1).
定义2设函数b∈Lipβ(µ)(0<β<1),定义相应的参数型Marcinkiewicz积分交换子

定义3设以及非负整数表示不超过x的最大整数).函数a(x)∈Lq(µ)称为一个(p,q,s)原子,如果满足下列条件:
(3) 当|γ|≤s时,有
定义4原子Hardy空间的定义为
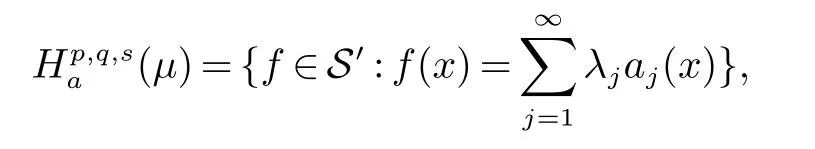
其中aj是(p,q,s)原子且
定义5对0<α<∞,定义与非倍测度µ相关的分数次积分Iα为
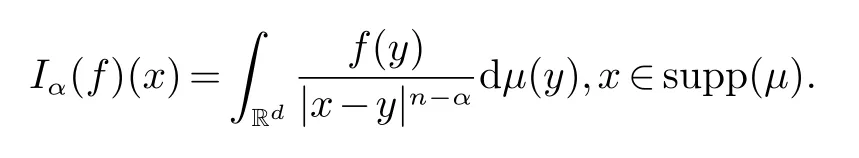
引理1假定0<α

引理2设分布f属于当且仅当存在(p,q,s)原子aj和常数λj满足


其中下确界取遍f的所有原子分解.
引理3设核函数K(x,y)满足为(6)式所定义的参数型Marcinkiewicz积分交换子,

注记1引用引理1,很容易验证引理3的结论,这里略去证明过程.
全文中,C表示与主要参数无关的常数,其值在不同的地方可能不尽相同.对任意µ可测集合E,χE表示其特征函数.对于固定的p满足表示p的共轭指数,即
1 主要结果和证明
首先给出本文的主要定理:
定理1设K(x,y)满足(2)和(3),为(6)式中定义的参数型Marcinkiewic积分交换子.假设Mρ在L2(µ)上有界则对有

证明设a(x)是一个(p,2,0)原子,即a(x)满足0.则存在与a无关的常数C>0使得不妨设由于
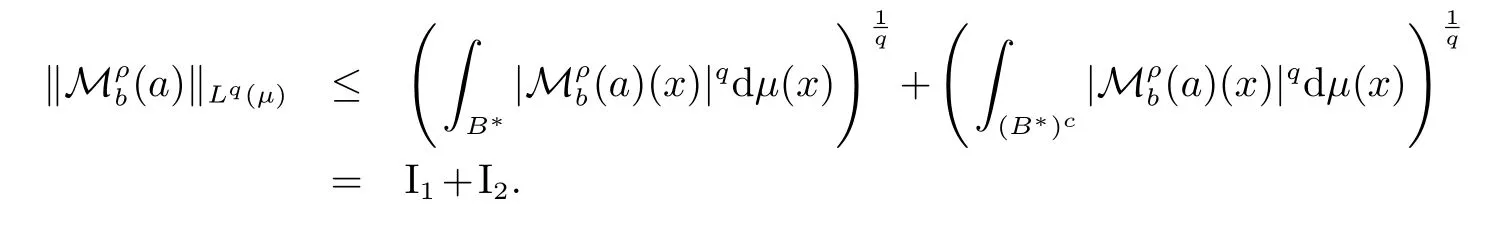
对于I1,取和q1使得则由Hlder不等式,引理3以及a(x)的尺寸条件知

再来估计I2,
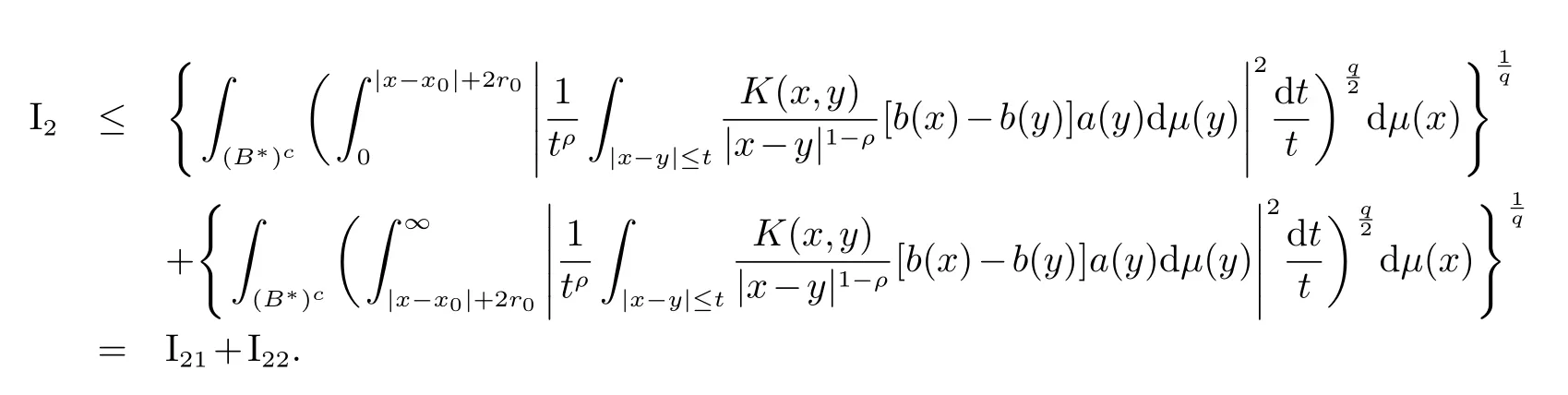
注意到x∈(B∗)c和y∈B,有|x−y|∼|x−x0|∼|x−x0|+2r0,于是对I21,有
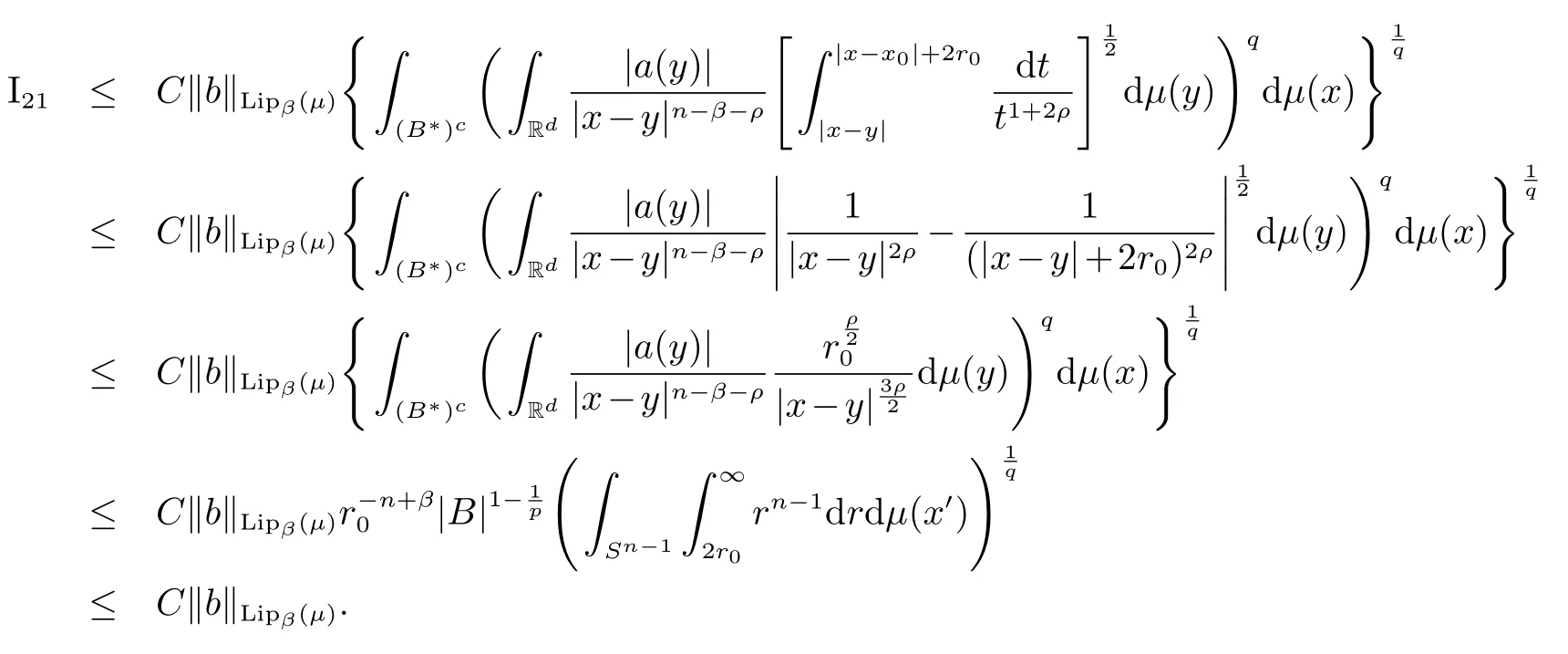
对于I22,利用原子的消失性以及|x−x0|+2r0 对于II2,类似于I21的估计,有 下面估计II1,有 对于II11,有 对于II12,有