WSNs中基于Chebyshev多项式的可认证密钥协商方案∗

郭学让，汪烈军，葛潇艺

(新疆大学 信息科学与工程学院，新疆 乌鲁木齐830046)

0 引言

随着无线技术和传感器技术的发展，无线传感器网络（Wireless Sensor Networks,以下简称WSNs）已被广泛应用于军事、环境监测、交通管理、医疗护理和国土安全等领域.由于传感器节点常被部署在不安全的区域，所以保证传感器网络中信息的安全传递至关重要.因此，寻找一种适合当前WSNs的节点认证和密钥协商方案是无线传感器网络安全研究的热点之一.

WSNs的密钥协商方案主要分为基于密钥预分配的密钥协商方案和基于公钥系统的密钥协商方案.由于密钥预分配方案存在网络拓展性差、存储量大等不足，安全强度更高的公钥密码体制被越来越多的应用于WSNs中.但受到传感器节点在计算能力、通信带宽以及能量供给方面的限制，不易采用传统意义上的公钥密码体制[1].

Oliveira等人[2]利用双线性对实现了基于身份的非交互式密钥管理方案，并证明了它可以完全适用于无线传感器网络.文献[3]通过对双线性类认证密钥协商协议的评估，得出方案虽然安全性较高但是双线性运算是非常消耗节点资源的结论.一些密钥协商方案为降低消耗没有引入双线性对，但降低了方案的安全性[4].传统的混沌密码系统中Chebyshev多项式的计算开销相对较校 可以用来替代WSNs密钥协商协议中的双线性配对，且不降低协议的安全性.文献[5]首次将Chebyshev多项式引入WSNs的密钥协商当中，但此方案对密钥生成中心要求较高且在安全方面存在一定缺陷.

基于上述讨论，本文提出一种安全性更高的基于Chebyshev多项式的可认证密钥协商方案.首先对Chebyshev多项式的定义及性质进行介绍，其次对文献[5]提出的的方案进行分析并提出本文的方案，最后对所提方案进行对比分析，证明本方案是安全可行的.

1 Chebyshev多项式的定义及性质

1.1 Chebyshev多项式定义[6]

令n=z且x∈[−1,1]，Chebyshev多项式Tn(x):[−1,1]→[−1,1]的递推关系式为：

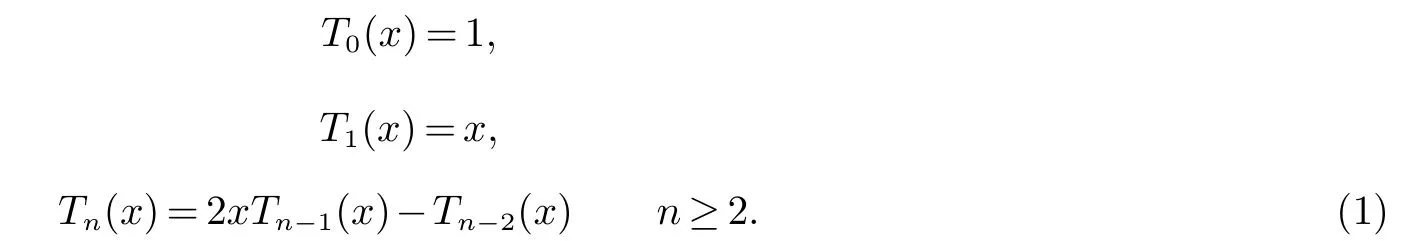
开始的几个Chebyshev多项式为：

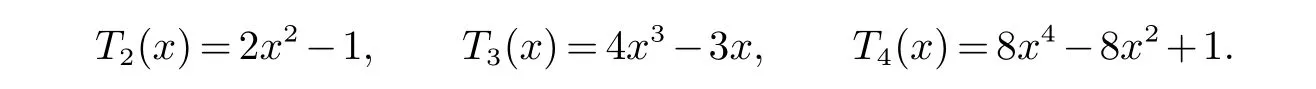
由于Chebyshev多项式是代数多项式，因此，可以将（1）拓展到有限域ZP上，这里的P为素数.

1.2 有限域上的Chebyshev多项式定义

令x,n∈ZP,n≥2，P为素数，则多项式Tn(x):Zp→Zp的递推关系为：

1.3 Chebyshev多项式的矩阵形式[7]

由Chebyshev多项式的定义：可写出递推公式的矩阵形式：

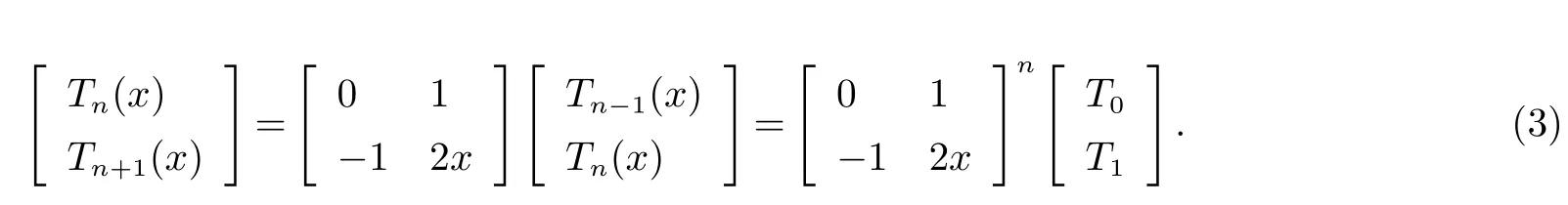
通过系数矩阵的n次方可以求得Tn(x)的值.再对Tn(x)取模P便可求得有限域中Chebyshev多项式的值，这样可以大大提高运算效率.

1.4 半群特性

Chebyshev的半群特性可表示为:

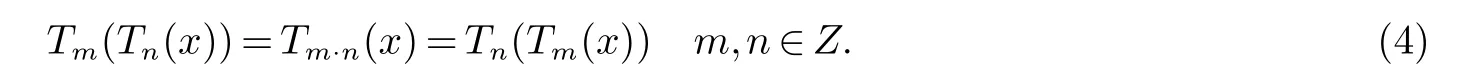
将此性质拓展到有限域上，令x,m,n∈Zp,m,n≥2,

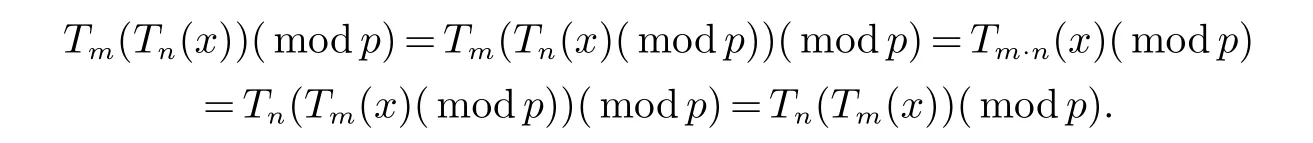
半群特性是有限域上Chebyshev多项式可以成为认证和密钥协商的基础.

1.5 计算上的单向性[8]

有限域Zp上的任意一个Chebyshev多项式还可表示为：

有限域上的Chebyshev多项式仍是混沌映射，现阶段并没有找到有限域上Chebyshev多项式的反函数表达式，因此在(5)中，已知x和n求Tn(x)相对容易，但如果已知x和Tn(x)求n是相当困难的，其求解困难性可与求离散对数的问题相当.由于计算上单向性的存在，所以Chebyshev多项式可以应用到密码学中.

2 已提出的方案

下面介绍一种基于Chebyshev多项式的无线传感器网络密钥协商方案，该方案通过密钥生成中心对密钥管理进而实现节点与节点之间的密钥协商，方案如下[5]：

在一个节点总数为N的网络中，每个节点都保存自己相应的随机数xt,rt∈Zp,t∈[1,N]和大素数P.节点A与节点B进行密钥协商，A和B的随机数必须要满足xArA=xBrB(modp).

1）密钥生成中心分别生成节点A与节点B的公钥:

2）私钥生成：IDA是A的身份信息，散列函数H:{0,1}→Zp密钥生成中心生成A的私钥：skA=skA1=skA2.其中

A保存xA和skB,节点B用同样的方法生成私钥.

3）节点A密钥的建立：选择随机数并计算:

A生成会话密钥KAB并将(σ1,σ2)发送给B.

4)节点B收到(σ1,σ2)后，验证方程：

若方程成立，则B计算会话密钥

上述方案虽然可以抵抗篡改和窃听攻击，但仍存在一些问题：

1)为了保证各个节点之间的通信，每对节点之间都要有不同的xt,rt∈Zp,t∈[1,N]且必须相互满足xArA=xBrB(modp)，这样每个节点必须保存该网络内其他节点的公钥和与之对应的私钥，这样加大了存储开销.

2)不能抵抗重放攻击，由于协商过程中节点A所选取的节点B并不确定，所以所发送的信息若被攻击或者截获，攻击者可多次向节点B发送(σ1,σ2)，当节点B收到信息后会不断的进行运算，最终导致能量耗尽.

3 本文方案

3.1 案描述

本文提出的方案网络模型[9]是由基站（BS）和大量具有身份标识的节点组成的.其中基站为可信任第三方且不考虑消耗，分别可以与网络内的各个节点进行通信.节点A与节点B进行认证与密钥协商的流程如图1所示.

1）节点A使用与基站共享的密钥向基站发送自己的身份信息IDA和要认证的节点身份信息IDB.

图1 密钥协商流程

2）基站收到来自A的信息后用与节点A的共享密钥解密，同时生成随机大整数a和大素数P，计算S=Ta(G)modp，并用与节点相应的会话密钥将信息加密发送给节点A与节点B.

3）节点B收到信息后用与基站的共享密钥解密信息，同时随机生成并保存大整数M，并计算M=Tm(S)modp，将M与IDB发送至节点A.

4）节点A随机生成并保存大整数n，计算N1=Tn(M)modp,N2=Tn(S)modp，在有限域上对N1、IDA、IDB进行Hash变换生成散列值：H(IDA,IDB,N1)，节点A与节点B的会话密钥就为KAB=N1，将N2与H(IDA,IDB,N1)发送至节点B.

5）节点B收到信息后计算H(IDA,IDB,Tm(N2))modp，并验证与H(IDA,IDB,N1)是否相等，若相等则完成认证，并得到会话密钥KBA=Tm(N2)modp，完成密钥协商.

3.2 合理性分析

步骤3中节点B的私钥为m，公钥为M，步骤4中节点A的私钥为n,公钥为N2.其中M=Tm(S)modp,N2=Tn(S)modp.

当节点A收到B的公钥时，可通过自己的私钥计算得到会话密钥.同理B可计算得到会话密钥.由Chebyshev多项式的半群特性可得：

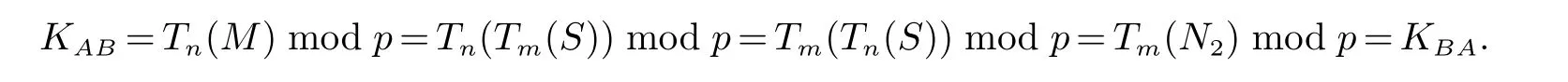
3.3 安全性分析

1）私钥的安全性

有限域中Chebyshev多项式具有单向性，既已知x和Tn(x)求n是相当困难的，其求解困难相当于求解离散对数问题.所以节点的私钥是保密的，不会由公式反推得到.节点A和节点B随机生成的大整数m、n只有节点本身知道，保证了计算所得会话密钥的安全性.

2）抵抗窃听攻击

步骤1与步骤2中采用密文传输，攻击者无法获得有用信息.步骤3与步骤4中采用非对称密码体制进行密钥协商，会话密钥不会直接在信道传送，而是由各个节点通过自己的私钥计算得来，所以即便攻击者截获了节点A与节点B之间传送的信息也无法得到有用信息.

2）抵抗篡改

步骤4中通过对节点身份信息以及N1进行hash变换生成散列值，步骤5中节点B进行运算时，可以验证信息是否遭到篡改.

4）抵抗重放

重放攻击指攻击者截获通信信息后，在下次的通信中冒充原节点发送给接收节点一个已接收过的信息，使接收节点误以为是原节点发送来的信息，达到冒充身份、欺骗系统的目的.多次向接收节点发送同一条消息，可造成接收节点进行不断计算，最终导致节点能量耗尽.本方案在每次认证过程中由基站提供一个随机数a、致使每次的认证信息都不相同，若接收节点收到重复信息，可以认为是攻击者发送的假冒信息，拒绝计算，使重放攻击失效.

3.4 存储开销

文献[5]中每个节点需要保存网络内每个节点的身份信息、公钥以及相对应的私钥，本文方案每个节点只需保存网络内各节点的身份信息即可.

3.5 计算开销

计算开销也就是计算的次数，分别用PE、Pcp、P∗、PHash表示进行一次对称加密或解密操作，进行一次Chebyshev多项式操作、一次乘法操作、一次Hash变换所需要的能量.文献[5]的节点A进行了5次多项式运算一次乘法运算和一次Hash变换.本文提出的方案进行了两次多项式运算、一次Hash变换、一次对称加密和一次解密操作.因为PE为对称加密操作，计算量相对较小，所以在运算量方面PE

表1 计算开销对比

4 结论

通过对Chebyshev多项式性质和WSNs密钥协商方案的研究，针对对称密钥管理中安全性的不足，以及有限域中Chebyshev多项式良好的的混沌特性、半群特性和在计算上单向性，提出一种节点之间的可认证密钥协商方案，并通过理论分析和同类方案的对比，证明本方案是安全可行的.