一道“伪抛物线”考题的思路解析与命题导向

☉江苏省苏州市高新区实验初级中学李树平

一道“伪抛物线”考题的思路解析与命题导向

☉江苏省苏州市高新区实验初级中学李树平

近读《中学数学》（下）2015年第5期，陈海宏老师在文1中从一道“伪坐标系”考题说起，列举了不少“坐标系搭台，平面几何唱戏”的考题，笔者十分欣赏作者的成文视角，并链接式阅读了文1中提及的“参考文献”（见文2～6），也感动于《中学数学》近一段时间密集刊发命题商榷文章，这对当前命题过程中的跟风、迎合、抄袭等不良现象起到有效的批判，也促进了有命题兴趣的同行深入研讨命题.作为一种实践跟进，本文以近期关注到的苏州市某区一道中考模拟卷的把关题为例，给出思路解析并给出命题商榷，就教于大家.

一、模考题解析与解后反思

模考题（2015年苏州市某区中考模拟卷第29题）如图1，抛物线10与x轴的一个交点为A，与y轴的交点为B.过点B作BC//x轴，交抛物线于点C，连接AC.动点P、Q分别从O、C两点同时出发，动点P以每秒4个单位的速度沿OA向终点A移动，动点Q以每秒1个单位的速度沿CB向点B移动，当点P停止运动时，点Q也同时停止运动.线段PQ与OC的交点为D，过点D作DE//x轴，交AC于点E，射线QE交x轴于点F.设点P、Q移动的时间为t（单位：秒）.

（1）直接写出点A、B的坐标.

（2）在点P、Q移动的过程中.

①当四边形CEDQ为平行四边形时，求出t的值；

②当△PQF为等腰三角形时，求出t的值.

图1

思路简析：（1）A（18，0），B（0，-10）.

（2）①容易发现四边形CAPQ和四边形CEDQ都是平行四边形，此时有PA=QC=DE.由PA=18-4t，QC=t，可得方程18-4t=t，解得，问题获解.

因为△QDC∽△PDO，△QEC∽△FEA，所以QC PO=，所以PO=FA，所以PF= PA+FA=PA+PO=OA=18.（注意：求出PF的值为定值是很关键的，这涉及后续用含t的式子表示其他线段）

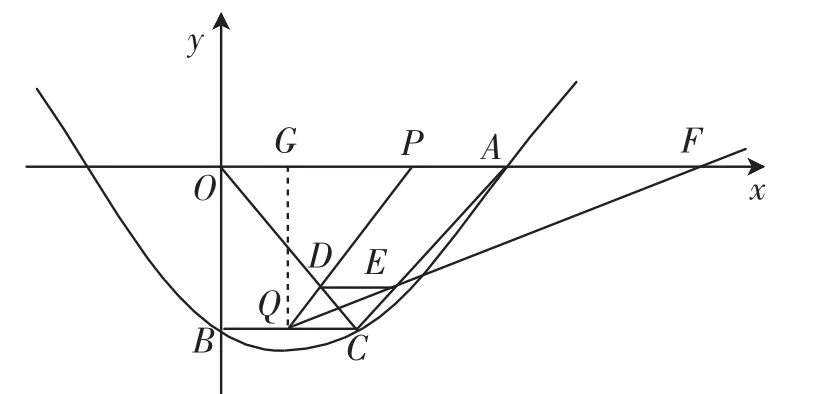
图2

因为QC=t，PO=4t，PF=18，QG=10，所以在Rt△PQG和Rt△FQG中，有PQ2=PG2+GQ2=（4t-8+t）2+102=（5t-8）2+ 102；FQ2=FG2+GQ2=（18+4t-8+t）2+102=（5t+10）2+102.（注意：这里的运算量较大，而且线段PQ、FQ的平方不宜匆忙展开，将影响后面所列一元二次方程的简化求解）

解后反思：排除无关信息或线条的干扰，可以将“模考题”的图1重新画成图3，就是在直角梯形AOBC中，BC=8，OB=10，OA=18，其余运动方式及生成图形同“模考题”表述.

图3

这时是否发现“模考题”题干中那条抛物线没有了！可怜的抛物线虽然出现在题干中，然而却过早的“死去”，整个问题的难点设计只是在一个几何题上.想来，将这类问题称之为“伪抛物线”问题应该是恰当的.

二、模考题溯源

作为一个有着多年毕业班教学经历的笔者，在独立演算“模考题”之后，总是有“似曾相识燕归来”的感觉，办公室同事用手机拍题软件迅速检索到几十道同类考题，在百度上也很方便地就检索出大量同类考题，不妨列举几个有代表性的高度相似题：

例1（2009年湖南省怀化市中考题）如图4，在直角梯形OABC中，OA//CB，A、B两点的坐标分别为（15，0），（10，12），动点P、Q分别从O、B两点出发，……（限于篇幅，略去部分运动的题干描述）设动点P、Q运动时间为t（单位：秒）.

（1）当t为何值时，四边形PABQ是等腰梯形，请写出推理过程；

（2）当t=2秒时，求梯形OFBC的面积；

（3）当t为何值时，△PQF是等腰三角形？请写出推理过程.

图4

例2（2010～2011学年广东省珠海一中高三（下）第一次调研数学试卷（理科）第17题）题干、图形及标注字母与“模考题”完全相同.设问如下：

（1）求A，B，C三点的坐标和抛物线的顶点坐标.

（2）当t为何值时，四边形PQCA为平行四边形？请写出计算过程.

（4）当t为何值时，△PQF为等腰三角形？请写出解答过程.

例3 （2012年湖北省谷城县中考适应性考试第26题）题干、图形及标注字母与“模考题”完全相同.设问如下：

（1）（2）同“例2”；（3）同“例2”第（4）问.

三、命题导向之思

通过上面的解析、反思与溯源，不难发现，“模考题”只是一道复制后简单改变设问的“拿来主义”，并不是一道有原创或深度改编的把关题，结合考题溯源，早在2009年中考卷就曾有类似的动态几何问题出现，而到了一份高三模拟卷中，却融入所谓的抛物线背景，拼凑式试题出现了，接着在2012年湖北省谷城县继续传播这类考题，时光到了2015年，经济发达的苏州市某区在中考模拟考卷的最后一题，仍然在传播.以下再围绕这道“模考题”给出两点命题导向之思考.

1.重视地区模考命题，指明复习备考方向

我们知道，地级市中考统一命题是当下的主流形式，然而作为应考的一种专业指导，地级市所辖的县区常常在中考前两个月左右会组织相应的高仿真模拟考试，根据这样的模考，广大备考师生会重新思考自己的复习策略.所以各县区中考模考命题工作就显得十分重要，务必为广大备考师生指明复习备考方向，真正诊断出考生的问题，查漏补缺，既要重视课标的刚性要求，又要贴近本地区的中考试题风格.切记不能直接拿来，复制粘贴或者简单改编（像上文中“模考题”这样的图形、字母、数据都不改动，而且还是6年前就曾有过的中考原题），这样下来，只会把广大备考师生引向题海，多做、多练就会碰到原题、高仿题或同类题，复习备考的导向走偏已不可避免.

2.思辨伪坐标系问题，追求题干充满活力

就“模考题”来说，所谓的抛物线只是为了给出几个点的坐标，其余问题探究则与抛物线无关，只是在繁杂线条上增加了干扰，这种拼凑式的命题取向已被很多有识之士批判多次.因为无论从数学的本质追求简洁（比如美籍华人数学家丘成桐先生就曾指出“好的数学是简洁的”），还是从“好的题目”应该追求简洁呈现、自然生长、渐次展开、易进难出等特点（章建跃语），而且对于一道综合题，题干能否充满活力也应该成为一种命题追求.

1.陈海宏.一道“伪坐标系”考题引发的思考［J］.中学数学（下），2015（5）.

2.邬吉利.一类“伪坐标系”考题的评析与商榷［J］.中学数学（下），2014（8）.

3.严冬梅.命题到底该怎样考查概念——以七年级上学期一些习题为例［J］.中学数学（下），2015（3）.

4.仲进东.例谈客观题型中“把关题”的呈现方式［J］.中学数学（下），2015（3）.

5.闫守范.新定义题破题策略与命题商榷［J］.中学数学（下），2015（3）.

6.王文清，邢成云.中考命题需谨慎一石三鸟当思量——以2014年滨州市中考数学试题为例［J］.中学数学（下），2015（3）.

7.贺信淳.从多角度审视一道中考试题说开去——谈对初中数学教育现状之惑［J］.数学通报，2013（12）.