理解教材“双主线”，夯实“双基”思“四基”——以“解一元一次方程（第1课时）”教学为例

☉江苏省射阳县实验初级中学　郭丰胜

理解教材“双主线”，夯实“双基”思“四基”
——以“解一元一次方程（第1课时）”教学为例

☉江苏省射阳县实验初级中学郭丰胜

最近一次教研活动中，笔者执教“解一元一次方程（第1课时）”，得到与会同行的好评.本文先呈现该课时的教学预设，进一步展开课后反思，与更多同行研讨交流.

一、“解一元一次方程（第1课时）”教学预设

（一）教学目标

（1）知道解方程的目标形式“x＝a（常数）”；

（2）掌握解方程的一般步骤“合并同类项”“系数化为1”，并能较快速地解形如“ax＋bx=c＋d（a、b、c、d为常数，a＋b≠0）”的方程；

（3）会列一元一次方程解简单的问题；

（4）在解方程时体会转化思想，在列方程解应用问题时感受方程模型的应用价值.

（二）教学重点与难点

重点：学会“合并同类项”和“系数化为1”解一元一次方程，并向学生强化解一元一次方程的目标形式是“x＝a（常数）”.

难点：会列一元一次方程解简单应用问题，特别是应用问题中含两（三）个未知量，且它们之间互相关联，如何恰当设出一个未知数表示多个未知量列出方程，并解方程和完成解答.

（三）教学流程图

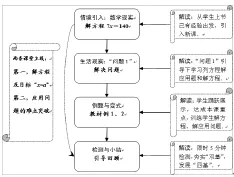
（四）教学过程

环节1：课堂导入（预设用时2分钟）.

解方程：（1）7x＝14；

追问：你们是怎样解的？依据是什么？转化的目标是什么？

【预设】在学生答出解法依据后，通过PPT动画展示.

【预设意图】利用学生已有的知识经验，让学生根据“等式性质2”解方程，并通过追问得出解方程的转化目标形式是“x＝a（常数）”.

环节2：生活现实（预设用时8分钟）.

问题1：某校三年共购买计算机140台，去年购买数量是前年的2倍，今年购买数量又是去年的2倍.前年这个学校购买了多少台计算机？

思路启发：问题中有几个未知量，它们之间有何关系？

引导反思：第一，问题中的等量关系是什么？第二，解方程的目标是什么？第三，解方程时每步的依据是什么？合并同类项起了什么作用？

【预设意图】启发学生思考，设出恰当的未知数，并表示出不同的未知量，从而列出方程.这个环节以教师主导追问为主，通过教师追问学生，启发思考，促进学生想得更合理、更深入.

环节3：例题与变式（预设用时26分钟）.

【预设】在方程旁边动画呈现如下变式.

例1（2）7x-2.5x＋3x-1.5x＝-15×3-6×3.

例2有一列数，按一规律排列成1，-3，9，-27，81，-243，…，其中某三个相邻的数和是-1701，这三个数各是多少？

教师启发学生思考：已知三个数中的某个，就能知道另两个吗？

例2的变式1：（引语：这列数中某相邻三个数的和可能为正数吗？）有同学说“这列数中某相邻三个数的和可能为63.”你觉得呢？

例2的变式2：（出示教材第88页，练习2）某工厂的产值连续增长，去年是前年的1.5倍，今年是去年的2倍，这三年内总产值为550万元.前年的产值是多少？

（学生独立思考1分钟后）追问一个学困生：这个问题中有几个未知量，你能不能用含一个未知数的式子表示这几个未知量？

例2的变式3：（教材第91页，复习巩固第6题）洗衣机厂今年计划生产洗衣机25500台，其中Ⅰ型、Ⅱ型、Ⅲ型三种洗衣机的数量比为1∶2∶14，计划生产这三种洗衣机各多少台？

【预设】问题呈现后，继续给出思考“有同学认为这个问题跟前面的都是‘一样的’”，你觉得他为什么说“是一样的”？

【预设意图】例题教学重视启发引导，学生展示，变式训练，突破难点，巩固新知.这个环节将以学生踊跃展示为主，教师引导学生围绕本课的两条核心主线展示和交流.

环节4：检测与小结（预设用时9分钟）.

限时检测（5分钟），来自教材第88页，练习1（4小题）.

课堂小结从如下三个角度进行.

（1）今天学了解方程的哪些步骤？解方程的转化目标是什么？

（2）解应用问题时，对于互相关联的几个未知量，如何用同一个未知数来表示它们？

（3）数学史话链接：关于“对消”与“还原”.

【预设意图】限时检测是落实“课标（2011年版）”的“传统双基”中的对学生基本运算能力的要求；同时安排几个小结问题又是重视“课标（2011年版）”的“四基”中强化学生的转化思想及基本活动经验的积累与分享.

二、课后反思

1.理解教材，“双主线”架构教学流程

备课之初，认真研习教材，前一节中学生已熟悉一元一次方程的概念，掌握了等式的基本性质，而且会利用等式的基本性质解简单的方程，这一节主要讨论两个问题：第一，如何根据实际问题列方程？这是贯穿全章的中心问题，也是讨论方程解法的背景；第二，如何解方程？

基于上述认识，具体到本节课，教学重点有两个，第一，讨论如何利用“合并同类项”和“系数化为1”解一元一次方程，并向学生强化解一元一次方程的目标形式是“x＝a（常数）”；第二，解简单应用问题，特别是应用问题中含三（两）个未知量，且它们之间互相关联，如何恰当设出一个未知数表示多个未知量列出方程，并解方程和完成解答.

2.理解学生，对话教学促进课堂生成

学生在小学阶段就已熟悉一些简单的一元一次方程的解法，在上一节又学习了利用等式的基本性质解简单的一元一次方程，对本课时将要学习的“合并同类项”“系数化为1”的解方程步骤并不陌生，只是重新规范了步骤命名和解法书写.而“问题1”以及“例2”这两个问题情境学生也有所涉及，只是以前多是从算术角度列算式求解，这节课将引导学生列一元一次方程解答.

3.研究课标，从夯实“双基”到发展“四基”

本课教学内容简单，特别是合并同类项这一步骤，很多学生在小学阶段就会了，只是没有给出明确的步骤或规范表达.我们知道数学的特征之一是“数学是一步一步向上走”（米山国藏语），在对“合并同类项”“系数化为1”这两步骤熟练掌握的基础上，继续向前走，学习移项、去括号、去分母等步骤时才能有扎实的基础，所以本节为解方程的起始课，不宜追求过快的教学进度，而要注重夯实“双基”，在课堂最后阶段我们安排了“限时检测”也意在此.另外，我们还通过小结阶段的几个问题，意在发展“四基”：促进学生积累和分享数学活动经验.

1.章建跃，陈向兰.数学教育之取势明道优术［J］.数学通报，2014，52（10）.

2.郑毓信.由“熟能生巧”到自觉学习：搞好数学教学的一个关键问题［J］.数学教育学报，1999，8（2）.

3.钟启泉.新旧教学的分水岭［J］.基础教育课程（上），2014（2）.

4.中华人民共和国教育部制定.义务教育数学课程标准（2011年版）［M］.北京：北京师范大学出版社，2012.

5.马立平，著.小学数学的掌握和教学［M］.李士锜，吴颖康，等，译.上海：华东师范大学出版社，2011.Z