基于“三个理解”，注重“自然生长”——区一节优课评比的实录、评析及感悟

☉江苏省淮安市淮海中学　张建华

基于“三个理解”，注重“自然生长”
——区一节优课评比的实录、评析及感悟

☉江苏省淮安市淮海中学张建华

一、背景介绍

2015年3月18日笔者有幸观摩了5节淮阴区优课比赛，划片比赛，借班上课，获评委一致好评的是开明中学的王老师这节课，上课内容是苏科版义务教育教科书数学八年级下册“10.2分式的基本性质（1）”.这节课是基于“三个理解”、注重知识的“自然生长”的一节优课，现将课堂实录及感悟整理成文，与同行交流研讨.

二、课堂实录

环节1：复习回顾

生1：3，6.

师：说说你的根据是什么.

生1：分数的分子、分母都乘以（或除以）同一个不为0的数，分数的值不变.

师：很好.分数的基本性质是什么？

生齐：分数的分子、分母都乘以（或除以）一个不为0的数，分数的值不变.

评析：教者理解学生，基于学生已备的“数学现实”，引导学生回顾分数的基本性质，为分式的基本性质探索提供类比的基础.这种为新知识学习服务的必要的经验和预备知识，称为“先行组织者”，能唤醒学生在分数基本性质方面的知识储备.

环节2：问题情境

师：请解决下面的问题.

一列匀速行驶的火车，如果t h行驶s km，那么2t h行驶2s km、3t h行驶3s km、…、nt h行驶ns km，火车的速度可以分别表示为______km/h、______km/h、______km/h、_______km/h.这些分式的值相等吗？由此你发现了什么？

评析：此问题情境贴近学生生活的情境，启发学生思考，激发学生探究的兴趣.

环节3：探索新知

师：由4个结果得到什么结论？

师：为什么？

生3：火车匀速行驶，速度相等.

生4：分式的分子、分母都乘以同一个数2、3或一个字母n，分式的值不变.

师：单项式是什么？

生齐：数与字母的积的式子.

师：单独一个字母或数字也是什么？

生齐：单项式.

师：多项式是什么？

生齐：几个单项式的和.

师：什么是整式？

生齐：单项式和多项式统称整式.

师：分式的分子、分母都乘以同一个数2、3或一个字母n，也就是说分式的分子、分母都乘以同一个什么？

生齐：整式.

师：对这个整式有什么要求？

生齐：不能为0.

师：为什么？

生5：如果整式为0，分式的分母乘以0为0，从而分母无意义，所以整式不能为0.

师：刚才是分式的分子、分母都乘以同一个不为0的整式，分式的值不变，还可进行怎样的运算？

生齐：除法.

师：你能概括出什么结论？

生6：分式的分子、分母都乘以（或除以）同一个不为0的整式，分式的值不变.

（师板书分式的基本性质：分式的分子、分母都乘以（或除以）同一个不为0的整式，分式的值不变）

师：你概括得太棒了！与分数的基本性质有什么异同点？

生7：不同点：一个是式，一个是数；相同点：一是都是乘法或除法，二是同一个不为0的数或整式.

师：说得很不错.分式的基本性质哪位同学能用式子来表示？

（教师强调C是不等于0的整式）

师：对于分式的基本性质的学习，我们可以类比分数的基本性质，同学们能否用分式的基本性质来解决一些问题呢？

评析：在新知识教学过程中，教者用“慢”节奏教学，调动学生积极参与知识的学习，并在恰当时机揭示学生已有数学知识与新知识之间的联系，通过讨论使学生理解从分数到分式是把“数”引申到“式”，分数是分式的特殊情形，即“从特殊到一般”，让学生经历类比分数的基本性质探索分式的基本性质的过程，有利于学生知识的建构，培养学生“类比”的推理能力.

环节4：应用新知

例1下列等式的右边是怎样从左边得到的？

师：（1）中为什么a≠0？

师：对，a≠0是一个隐含条件.

师：（2）中为什么a≠0？

师：说得很有道理.

评析：通过让学生个人思考、小组讨论、展示交流，使学生主动参与到学习活动中来，培养学生的合作交流意识和表达能力.

讨论：下列等式从左到右是否成立？为什么？

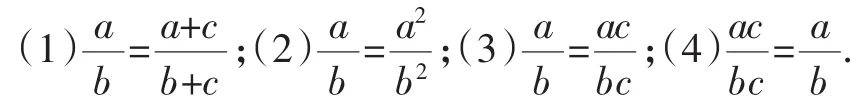
（小组讨论很热烈，老师留充足的时间给学生，老师在各小组间巡视）

生10：（1）不成立，因为分式的基本性质只能是乘除法，而（1）式是加法.

生11：（2）不成立，因为乘的不是同一个整式，分子乘以a，而分母乘以b.

生12：（3）也是不成立的.

（很多学生惊讶，有的学生笑，表示怀疑生12说错了）

师：你能说说是什么道理吗？

生12：少了c≠0这个条件.所以不成立.

师：（4）呢？

生13：（4）是对的，我说不出原因.感觉和（3）不一样.

师：（4）不也没有c≠0这个条件吗？

师：大家同意生14的说法吗？

生齐：同意.

师：（3）在乘c时，c≠0是要规定的，没说c≠0，所以（3）是不成立的；而（4）在除以c时，c≠0是一个隐含条件，所以不需要规定，（4）是成立的.

评析：此讨论是教者补充的，（3）、（4）很经典.教者“理解教学”，在解题过程中教师也是放“慢”节奏，给学生充足的时间，学生思考后说解法，老师在关键处作指点.特别引起学生认知上的“冲突”的是（3）、（4），“何时要规定”“何时是隐含条件”，通过学生合作交流，老师启发引导，明晰两者的区别，也培养学生谨慎的思辩的良好习惯.

巩固练习：

生15：2b，分子、分母都除以a.

生16：3ac，分子、分母都乘以c.

生17：a2+ab，分子、分母都乘以a.

（师板书a（a+b）=a2+ab）

生18：x，分子、分母都除以x.

（师板书x2+xy=x（x+y））

生19：（5）填a-b，分子分母都除以a-b.

（学生自主思考后完成，生说，师板书a2-b2=（a+b）·（a-b））

评析：（1）、（2）、（5）是教材上的练习题，（3）、（4）是补充的题目，教师灵活运用教材上的练习，此题组设计，由易到难，由浅入深，为实现真正的师生、生生之间的有效互动提供了保障，采用以练为主、讲练结合的方式，恰当板书关键知识点如（4）、（5）的因式分解，唤醒学生因式分解方面的知识储备，有助于学生知识的建构.

例2不改变分式的值，使下列分式的分子与分母都不含“-”：

生20：分子与分母都乘以-1.

生21：分子与分母都乘以-n.

师：分母又含“-”.

生22：分子与分母都乘以-1.

师：分母也含“-”.

评析：学生在解（1）时用分式的基本性质很容易，但在解（2）时，用（1）的方法时，将分子中化为不含“-”，但分母中又含有“-”，这也不符合题意，教者放手让学生思考解决，静待花开.分式的变号，是一个教学难点，也可类比“”，教师却舍而不用，值得商榷.

例3不改变分式的值，使下列分式的分子与分母的最高次项的系数是正数：（1）

分析：（1）中的分子x的系数是1，分母1-x2的项有1、-x2，1的次数是0，1=1·x0（师特别地板书了），-x2的次数是2，最高次项是-x2，要将-x2的系数-1变成“正”.

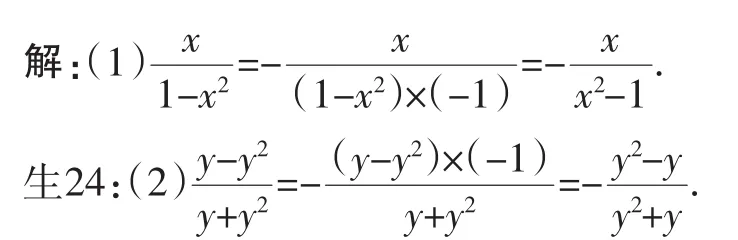
评析：此题有一定的难度，在解题过程中教师给学生较多时间，学生尝试解题，教师及时指导解题能力较弱的学生，帮助其克服困难.但有关“1的次数是0”，师特别地板书“”，此说法欠妥.

环节5：课堂小结

生25：分式的基本性质和它的应用.

生26：注意乘以或除以的整式不能为0.

生27：注意隐含条件和特别规定的区别.

……

师：利用从特殊到一般、类比的数学思想，学习分式时类比分数去学习.

评析：师生互动，锻炼学生的表达能力，让学生勇于发表自己的见解.

环节6：布置作业

三、几点感悟

1.加强过程教学策略

在“分式的基本性质”知识形成过程中，教者用“慢”节奏教学，以探究性学习为主，通过问题驱动，引导学生观察、猜想、验证和应用，从而获得知识.概念、性质的学习绝对不是简单的告知“结论”，而是经历知识产生、形成的过程，在经历中体验，在体验中感悟，在感悟中升华，教者能关注思想方法（如“从特殊到一般”“类比”）的回归，注重分数与分式知识的内在联系，关注数学教学规律的形成过程，让学生体验数学的理性，在“冰冷的美丽”的背后有着“火热的思考”.这也就是“三个理解”吧.

2.“教”是为“学”服务

教学的目的是“不教而会学”.本节课围绕“分式的基本性质及应用其对分式变形”自然展开，例题难度不大，但具有代表性，精讲精练，用学生自身具备的知识、方法去解决问题，将“类比”的数学思想渗透于教学之中，教师之道在于“调”，学生之道在于“悟”，能够调动学生积极思考，知识、方法由学生自己悟出来，这才是有效的教学.

3.设计铺垫，重视学生的思维参与

本节课以学生自主探究为主、教师引导与点拨为辅的方式进行，突出教师的主导和学生的主体关系，使学生在解决问题中获得更多的知识、方法、体验，虽然新课标提倡培养学生“发现问题、提出问题、分析问题、解决问题”的能力，但是在新知识建构过程中，难以期望学生提出问题，这就需要教师“铺路”，让学生“行走”.学生是学习的主人，是新知的建构者.

1.吴粉连.关于分式运算的教学思考——由学生分式化简题的订正说起［J］.中学数学（下），2014（11）.

2.高峰.参与过程设计，优化学习策略——以《平行四边形的判定（1）》教学为例［J］.中学数学（下），2015（1）.

3.何明.追求逻辑连贯、生长自然的教学设计［J］.中学数学教学参考（中），2015（3）.Z