多面开孔腔体孔缝耦合效应研究

陈旭来，周东方，胡 涛，焦彦维，朗国伟

(信息工程大学信息系统工程学院， 郑州450001)

0 引言

随着电子产品的精密度越来越高，电磁环境的日趋复杂，电子设备的电磁敏感度越来越低［1］。为了更好地进行电磁防护，研究电磁波对腔体孔缝的耦合机理，了解耦合效应的影响因素是十分必要的。对于孔缝腔体耦合效应的研究有许多方法，其中，等效传输线方法由于其简单方便的优点而被广泛采用。最早运用等效传输线法的是将孔缝等效为共面带状线，将腔体等效为终端短路的矩形波导，采用传输线理论对入射波对腔体的耦合进行了研究［2］，但是，研究仅限于计算垂直入射波对单面孔缝腔体中心点的耦合效应计算。其后，文献［3-7］对等效传输线法进行了扩展，使其能计算孔缝形状、孔缝数量、孔缝间距、电磁损耗等对电磁屏蔽效果的影响;文献［7-8］还对孔缝偏离体壁中心时的情形进行了考虑;文献［9-10］将等效传输线法扩展到了高次模的情形下。本文通过对等效传输线法的改进研究了入射波对多面开孔腔体的耦合效应。

1 多面开孔腔体等效传输线模型

1.1 多面开孔腔体孔缝耦合效应矢量分析

对于多面开孔腔体的耦合效应的分析首先对任意入射角度、任意极化角度的电磁波以及传播参数进行矢量分解，如图1所示。根据入射波的方位角φ、俯仰角θ，以及极化角Ψ，可以将入射波分解为x、y、z三个方向的分量［11］。

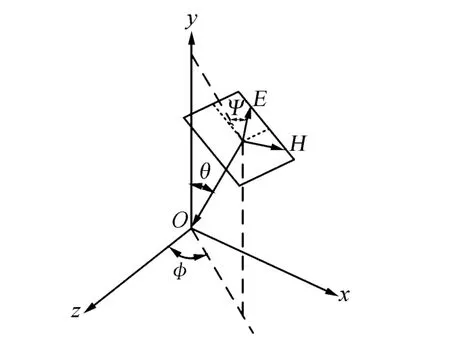
图1 入射电磁波的矢量分析

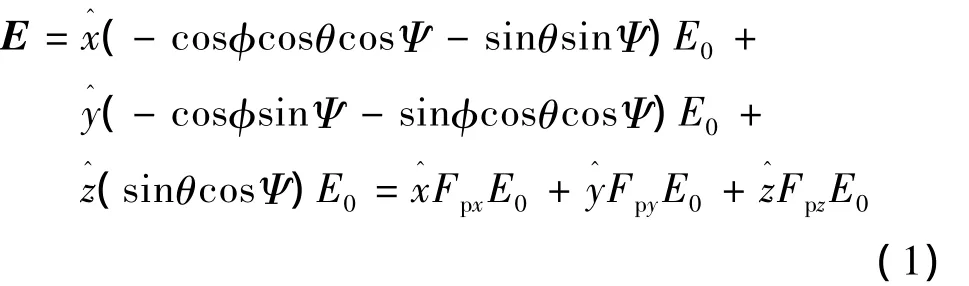
式中:E0为入射波场强;Fpx，Fpy，Fpz分别为 x，y，z三个方向的场强参数。传播常数β的分解为

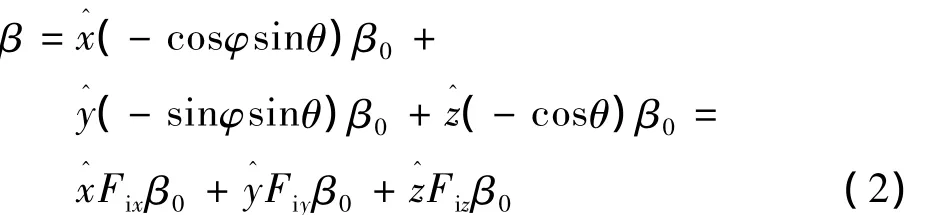
式中:β0为入射波的传播常数;Fix，Fiy，Fiz分别为 x，y，z三个方向的传播常数参数。

将入射电磁波进行矢量分解后，就可以根据不同方向的电场强度对腔体的耦合效应分别进行研究。如图2所示，z方向入射波从xOy面上的孔缝耦合进入腔体后可以产生x方向场强和y方向场强，根据孔缝等效偶极子理论可知z方向入射波耦合进入腔体产生的z方向场强很小，可以忽略不计，由于腔体尺寸以及孔缝尺寸的不同，需要分别采用等效传输线法计算不同方向的场强;同理可知y方向入射波从xOz面上的孔缝耦合进入腔体内后可以产生x方向场强和z方向场强;x方向入射波从yOz面上的孔缝耦合进入腔体内后可以产生y方向场强和z方向场强。

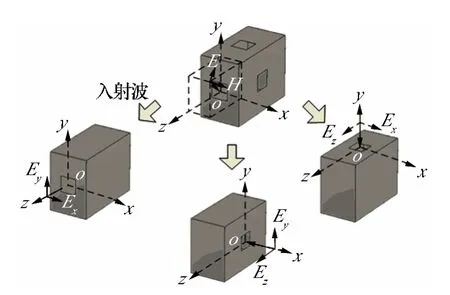
图2 多面开孔腔体矢量分析示意图

下面就x方向入射波分量对腔体yOz面孔缝的耦合进行计算，将孔缝等效为长为lapx的共面带状线，其特性阻抗为

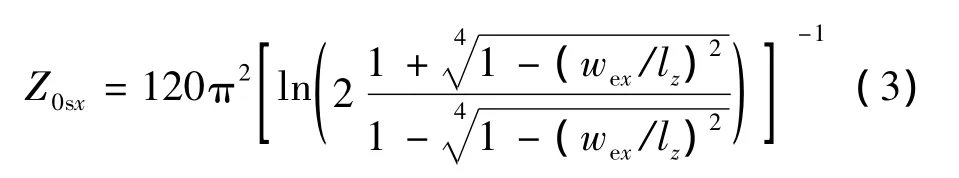
式中:wex为孔缝等效有效宽度。

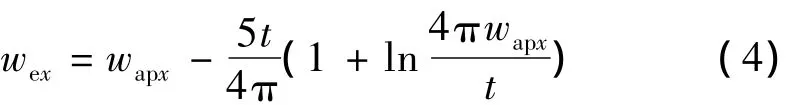
式中:wapx为孔缝的宽度;t为腔体壁的厚度。

根据孔缝与腔体之间的关系对孔缝特性阻抗进行修正可得孔缝等效阻抗。

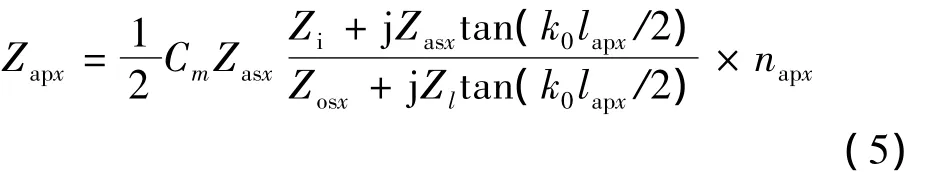
式中:Zl为腔体壁的表面阻抗，若腔体壁为良导体，其阻抗为零;若腔体壁为其他材质，则表面阻抗为

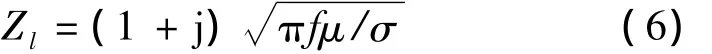
式中:μ，σ由腔体的材料决定;Cm为孔缝位置对耦合效应的耦合系数［6］。

在TEmnl模式下的等效特性阻抗和传播常数分别为

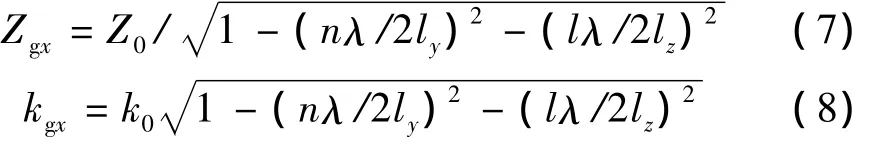
结合上述的Z0、V0和Zapx，将电磁波对腔体孔缝的耦合等效为电压和电阻的电压源对传输线的激励:V1x=V0Zapx/(Z0+Zapx)，Z1x=Z0Zapx/(Z0+Zapx)。

距离孔缝px，py，pz的观测点P点的等效电压和等效阻抗分别为

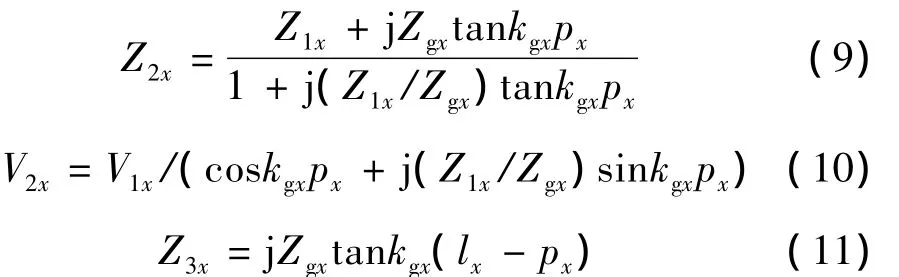
最终，可以得到P处的电压为

在TE模式下，矩形波导内任意位置的场强为［12-13］

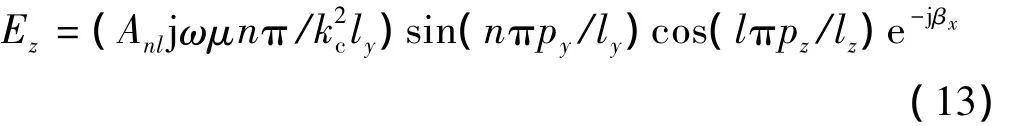
从中提取出表示观测点位置对屏蔽效能影响的参数

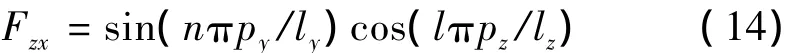
综合入射波场强参数Fpz、传播常数参数Fix以及位置参数Fzx进行计算，可得不同TEmnl下的Vzx

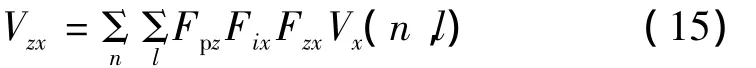
同理可得y方向入射波对腔体xOz面孔缝的耦合效应表达式Vzy，则入射波对多面开孔腔体耦合效应的z方向分量可表示为

将不同方向分量的计算结果进行矢量叠加可得多面开孔腔体内P点的屏蔽效能为

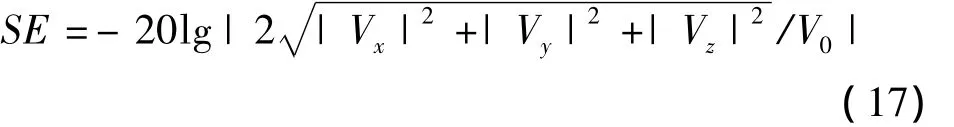
2 改进等效传输线法仿真验证

仿真矩形腔体如图2所示，腔体尺寸为lx=30 cm，ly=30 cm，lz=30 cm，腔体壁厚度为0.01 cm，孔缝尺寸为5 cm×5 cm。用CST仿真分析了多面开孔腔体的屏蔽效能，腔体材料设置为理想金属导体，背景材料为Normal，边界条件为Open边界，激励方式为平面波激励，场强为10 V/m，其中，Ex=-4.082 V/m，Ey=8.165 V/m，Ez=-4.082 V/m，极化方式为线性极化，计算频率范围为0 GHz～2 GHz，分别在腔体中心点和P点设置场强监视器，采用瞬态求解器进行仿真。将等效传输线法计算结果和仿真结果进行比对可得图3所示腔体中心点屏蔽效能图，由图可知，改进等效传输线法计算结果与CST仿真结果基本一致。根据式(18)可以求得表1所示不同模式下腔体谐振频率值。

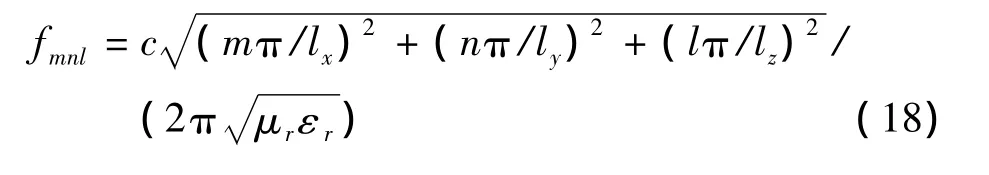
和屏蔽效能仿真结果进行比较可以发现:腔体屏蔽效能在谐振频率点最小，这是因为当入射波频率为腔体谐振频率时，入射电磁波通过耦合在屏蔽腔体壁上产生的等效磁流会通过散射进入腔体，由于相位相同，该散射场和腔体壁反射形成的场可以叠加，所以，腔体屏蔽效能较差。由于TE230，TE021，TE221谐振模式的场强极值点不在中心，所以，这三个谐振频率下不存在屏蔽效能极小值点。

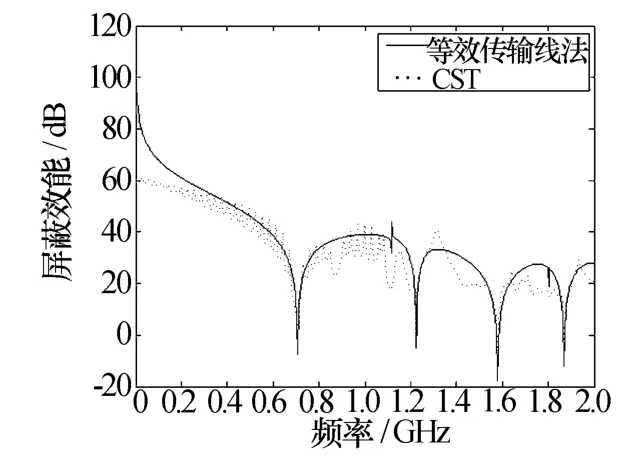
图3 腔体中心点屏蔽效能图

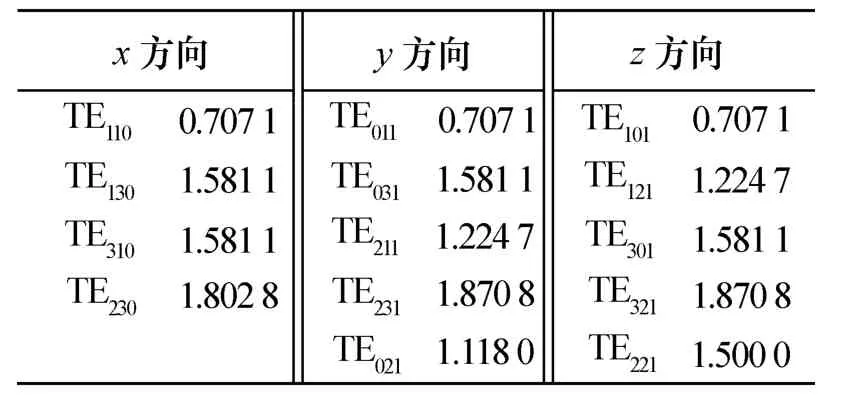
表1 腔体理论谐振频率值

将观测点位置设置为px=py=pz=20 cm，分别采用改进等效传输线法和CST仿真软件计算P点的屏蔽效能，如图4所示，等效传输线法所得结果和CST仿真结果基本吻合，当观测点位值不在腔体中心时，腔体的屏蔽效能极小值点比在腔体中心时要多，这是因为在TE230，TE021，TE221谐振模式下，观测点在场强极值的附近，所以，屏蔽效能出现极小值。

图4 腔体内任意点屏蔽效能图

2.1 多面开孔腔体屏蔽效能实验验证

采用实验对上述等效传输线法的正确性进行了验证，实验布局如图5所示。将多面开孔腔体置于微波暗室中，将探头至于腔体内指定位置，由频谱分析仪测量不同频率下腔体内的场强，根据式(19)将场强测量值换算成腔体的屏蔽效能值。

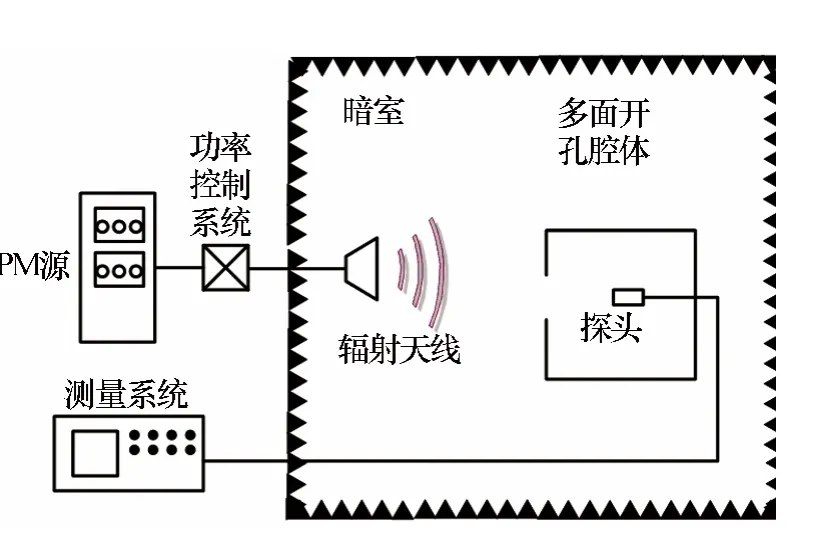
图5 实验布局图

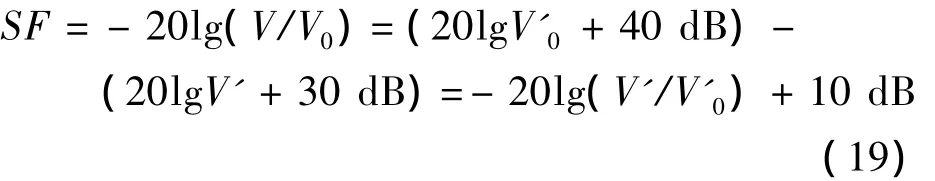
式中:V为腔体内同轴探头的实际耦合电压;V'0为直接暴露在HPM辐射场中同一位置的同轴探头的实际耦合电压;V'和V'0为它们经衰减器衰减后的测量电压值。分别将探头置于腔体中心和腔体内P点，P点坐标为px=py=pz=20 cm处，经测量可得腔体中心点屏蔽效能图和腔体内任意点屏蔽效能图，如图6、图7所示。

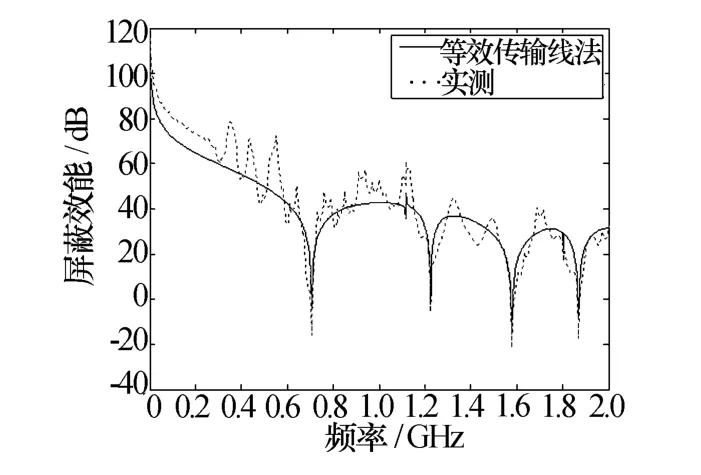
图6 腔体中心点屏蔽效能图

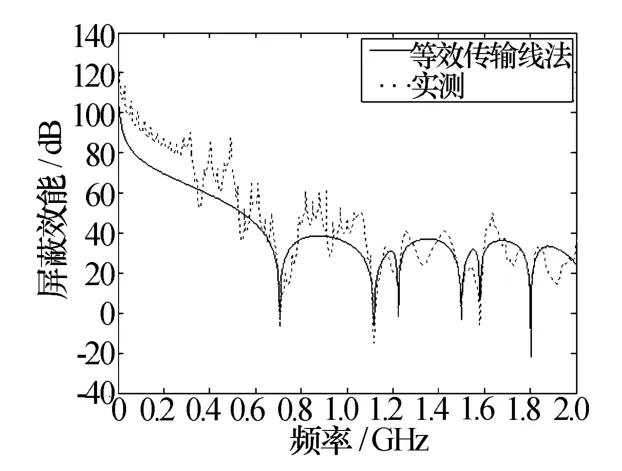
图7 腔体内任意点屏蔽效能图

由图可知，改进等效传输法所得结果和实验测量结果基本一致，当入射波频率为0.707 GHz、1.224 GHz、1.58 GHz、1.87 GHz时，腔体中心点屏蔽效能最差，而当观测点坐标为时腔体的屏蔽效能极小值点明显增多，这和上述理论研究结果基本一致，当观测点位置不是腔体中心时，由于其他谐振模式场强分布的影响使得腔体屏蔽效能极小值点增多。

2.2 不同腔体尺寸对屏蔽效能的影响

为了研究腔体尺寸对屏蔽效能的影响，采用等效传输线法计算相同体积下三种不同尺寸腔体的屏蔽效能，其中，腔体a尺寸为30 cm×45 cm×20 cm，腔体b尺寸为30 cm×36 cm×25 cm，腔体c尺寸为30 cm×30 cm×30 cm，三种腔体孔缝尺寸完全相同，均为7 cm×7 cm的正方形，入射波保持不变，经过计算可得如图8～图10所示的屏蔽效能图。

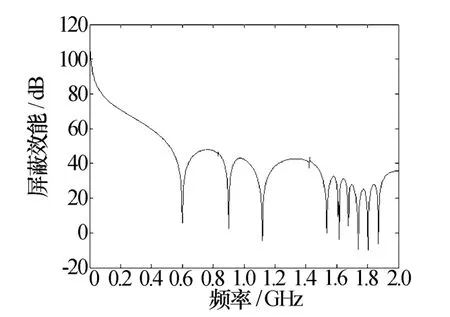
图8 腔体a屏蔽效能图

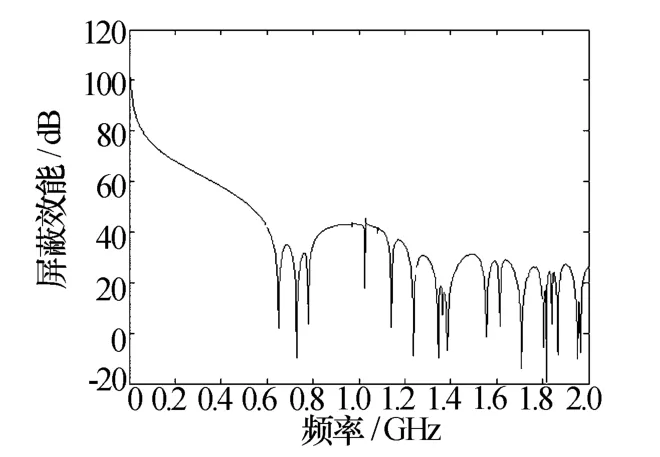
图9 腔体b屏蔽效能图

从图中可以看出，三种腔体的屏蔽效能值基本相同，但是腔体c的屏蔽效能极小值点要比另外两个腔体要少很多，这是因为腔体c为正方体，不同方向的谐振频率相同，从而减少了屏蔽效能极小值点。因此，相对其他尺寸腔体来说，屏蔽腔体为正方体时受电磁干扰的几率更小。

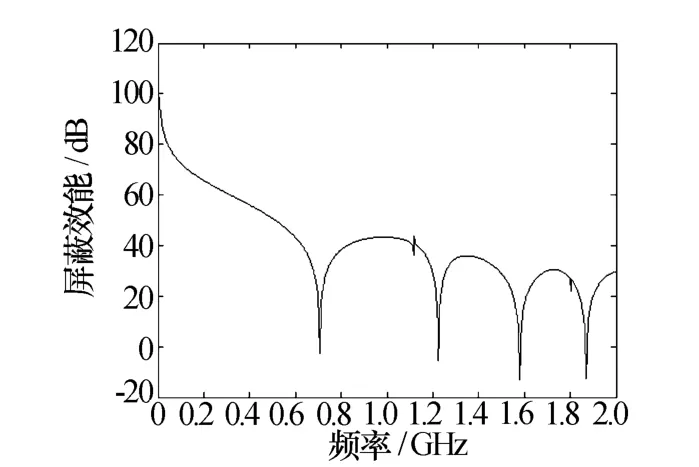
图10 腔体c屏蔽效能图

3 结束语

本文针对任意入射波对多面开孔腔体的孔缝耦合效应进行了研究，通过对入射波场强和传播常数的矢量分解将多面孔缝的耦合效应问题分解为不同面孔缝耦合效应的矢量叠加，根据矩形腔体谐振理论对已有文献中关于腔体内场强分布的研究进行了修正。将改进等效传输线法所得结果与腔体的理论谐振频率，CST仿真软件结果进行比较，验证了本文所提方法的正确性。由于本文综合考虑了多面开孔，腔体内场强分布等问题，使得等效传输线法具有更强的实用性，能在一定程度上指导屏蔽腔体的设计。

［1］刘尚合，刘卫东.电磁兼容与电磁防护相关研究进展［J］.高电压技术，2014，40(6):1605-1613.Liu Shanghe，Liu Weidong.Progress of relevant research on electromagnetic compatibility and electromagnetic protection［J］.High Voltage Engineering，2014，40(6):1605-1613.

［2］Robinson M P，Turner J D，Thomas D W P，et al.Shielding effectiveness of a rectangular enclosure with a rectangular aperture［J］.IEEE Electronics Letters，1996，32(17):1559-1560.

［3］Robinson M P，Benson T M，Christopoulos C，et al.Analytical formulation for the shielding effectiveness of enclosures with apertures［J］.IEEE Transactions on Electromagnetic Compatibility，1998，40(3):240-248.

［4］魏光辉，李 凯，潘晓东，等.含孔缝金属腔体电磁场增强效应的形成机理仿真［J］.高电压技术，2014，40(6):1637-1643.Wei Guanghui，Li Kai，Pan Xiaodong，et al.Formation mechanism simulation of electromagnetic field enhancement effect of metallic shielded enclosure with aperture［J］.High Voltage Engineering，2014，40(6):1637-1643.

［5］李 凯，魏光辉，潘晓东，等.带孔缝矩形金属腔体屏蔽效能研究［J］.微波学报，2013，29(4):48-52.Li Kai，Wei Guanghui，Pan Xiaodong，et al.Research of the shielding effectiveness of a rectangular metallic enclosure with an aperture［J］.Journal of Microwaves，2013，29(4):48-52.

［6］彭 强，周东方，侯德亭，等.带缝隙矩形腔的屏蔽效能传输线法修正及扩展分析［J］.强激光与粒子束，2013，25(9):2355-2362.Peng Qiang，Zhou Dongfang，Hou Deting，et al.Shielding effectiveness analysis of rectangular cavity with aperture by modification and expansion of transmission line method［J］.High Power Laser and Particle Beams，2013，25(9):2355-2362.

［7］Belkacem F T，Bensetti M，Boutar A G，et al.Combined model for shielding effectiveness estimation of a metallic enclosure with apertures［J］.IET Science，Measuremet and Technology，2011，5(3):88-95.

［8］Po'ad F A，Mohd Z M J，Christopoulos C，et al.Multimode consideration in the analysis of shielding effectiveness of a metallic enclosure with off-centred apertures［C］//International RF and Microwave Conference.Putra Jaya:IEEE Press，2006:306-310.

［9］Nie B L，Du P A，Yu T Y，et al.Study of the shielding properties of enclosures with apertures at higher frequencies using the transmission line modeling method［J］.IEEE Transactions on Electromagnetic Compatibility，2011，53(1):73-81.

［10］Belokour I，Lovetri J，Kashyap S.A higher-order mode transmission line model of the shielding effectiveness of enclosures with apertures［C］//IEEE International Symposium on Electromagnetic Compatibility.Mantreal Qwe:IEEE Press，2001:702-707.

［11］Shim J J，Kam D G，Kwon J H，et al.Circuital modeling and measurement of shielding effectiveness against oblique incident plane wave on apertures in multiple sides of rectangular enclosure［J］.IEEE Transactions on Electromagnetic Compatibility，2010，52(3):566-577.

［12］廖承恩.微波技术基础［M］.西安:西安电子科技大学出版社，1994.Liao Chengen.Theory of microwave technology［M］.Xi'an:Xidian University Press，1994.

［13］Grant I S，Phillips W R.电磁学［M］.刘岐元，王鸣阳，译.北京:人民教育出版社，1983.Grant I S，Phillips W R.Electromagnetism［M］.Liu Qiyuan，Wang Mingyang，translate.Beijing:People's Education Press，1983.