一种基于遗传算法的混合滤波器组设计方法

谭富春，吕幼新，杨皓翔

(电子科技大学电子工程学院， 成都611731)

0 引言

模数转换器(ADC)作为数字化电子系统的重要组成部分，是决定整个系统性能优劣的一个很重要的模块单元。随着现代电子技术的发展，对数据采集的精度和速率都提出了越来越高的要求，而受目前器件本身的限制，单片ADC很难同时满足高精度、高速率的采样要求。

Velazquez［1］提出了利用混合滤波器组(Hybrid Filter Banks，HFB)来实现高精度、高速率的模数转换系统，这也是目前备受学者们关注的研究重点和难点。文献［2］应用Z-S变换方法设计实现了模拟分解滤波器组，利用IFFT算法设计得到了数字综合滤波器的系数。此方法虽可实现不错的系统性能，但是在低频区域，滤波器组不具有很好的误差性能。文献［3-4］利用功率互补条件，通过两个全通滤波器相加减的形式完成了模拟分解滤波器的设计，实现过程较为繁琐。而且尽管混叠误差可达到-100 dB以下，但是失真误差很难满足高精度的ADC系统要求。

本文提出一种基于遗传算法优化设计5阶模拟分解滤波器的方法，利用IFFT设计了数字综合滤波器。通过仿真结果验证，所设计的混合滤波器组理论上可以满足24 bits的ADC系统要求。

1 基于功率互补的HFB的基本原理

HFB实现结构原理图如图1所示。输入的信号为带限信号，由模拟分解滤波器组将输入信号x(t)按照频率划分成M个子频带，然后用M片采样速率为f1=f/M=1/(MT)的ADC进行采样，其中，f为系统采样频率，f1为单片ADC采样频率。经过AD采样后的序列x1［n］通过内插，在序列之间均匀地插入M-1个0值。而综合滤波器将输入序列中含有的镜像频谱滤除掉，重构信号 y［n］。

在不考虑量化噪声情况下，输出y［n］的频域表示如下［5］

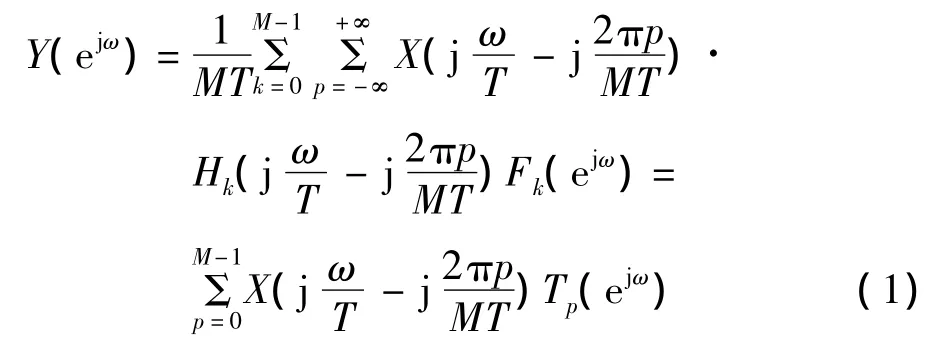
式中:ω=ΩT，ω为数字角频率，Ω为模拟频率;

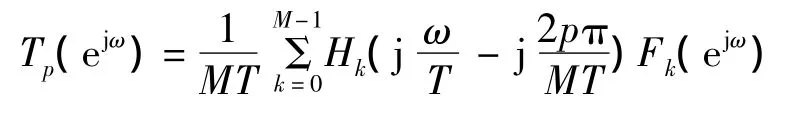
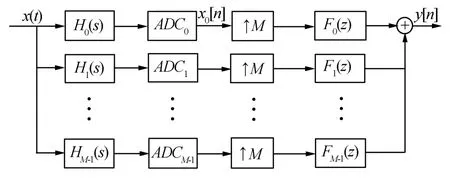
图1 M通道混合滤波器组的结构原理图

输出信号y［n］是由输入信号经过采样后频移后叠加而成的。如果要想获得理想的信号输出，则系统的传输函数Tp(ejω)必须满足一定的条件，即

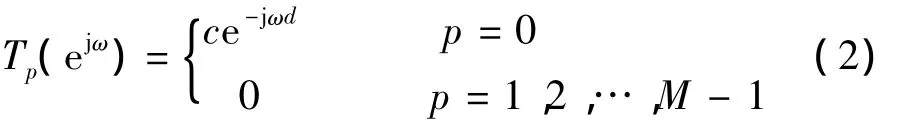
式中:c为尺度常数;d为系统延时。其中，T0(ejω)为系统失真函数，T1(ejω)，T2(ejω)，…，TM-1(ejω)为系统混叠函数。式(2)即为HFB ADC系统的完全重构条件。

1.1 基于功率互补的双通道混合滤波器组

当M=2时，忽略式(2)中的尺度常数，在不影响整体性能的前提下，为了便于推导分析，将定义采样周期T=1 s，双通道的HFB完全重构条件可以表示为［6］

当数字综合滤波器的频率响应可以设计成模拟滤波器频率响应的共轭，则在-π≤ω≤π范围内满足

结合式(3)、式(4)可得

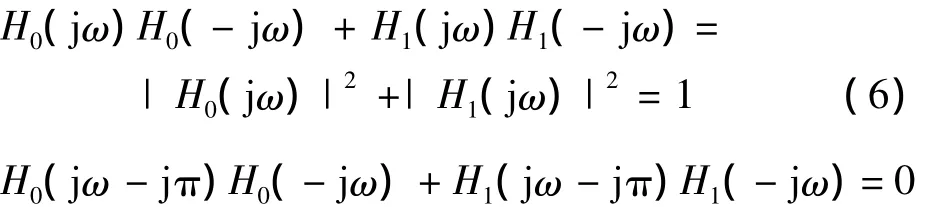
式(6)称为功率互补条件，满足此条件的模拟分解滤波器组称为功率互补型模拟分解滤波器组。

1.2 模拟分解滤波器的设计

根据上节功率互补条件，我们设计两个模拟滤波器的传递函数定义如下［7］

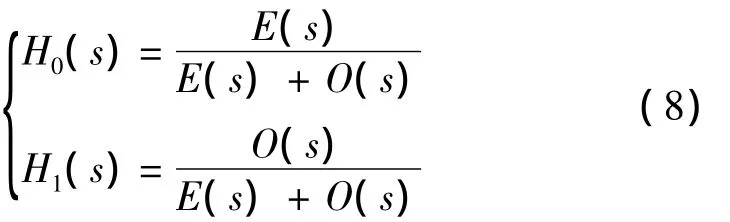
式中:E(s)和O(s)分别是分母多项式D(s){D(s)=的偶次项和奇次项。根据E(s)和O(s)的奇偶性和式(6)、式(7)很容易得到

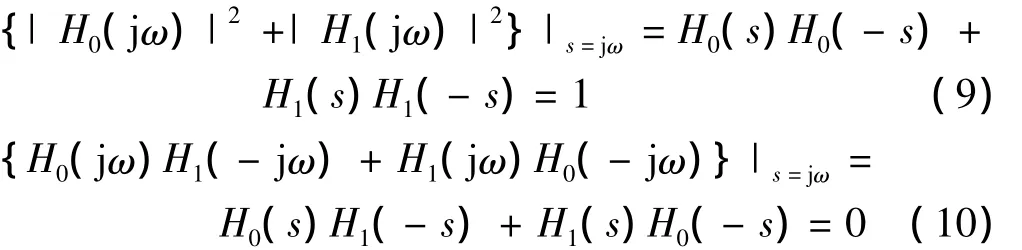
将式(10)、式(7)比较，如果模拟分解滤波器满足式(13)，则可以满足完全重构的HFB

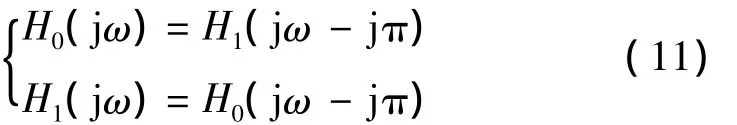
注意到模拟滤波器的频率响应是关于0频率点对称，因此，在实际设计中只需要满足其中一式即可。

1.3 应用遗传算法的模拟分解滤波器优化

遗传算法(Genetic Algorithm，GA)起源于用计算机对自然界生物做的仿真研究，在20世纪中后期，由密歇根大学的Holland教授所在的科研团队在基于生物遗传和自然选择的启示下提出了一种适合在繁杂系统优化应用的自适应概率技术——遗传算法［8］。其算法实质是一种并行、全局搜索的方法，可以在搜索过程自行积累有关搜索范围的经验，而且能够自适应地调整搜索方式以得问题的最优解。

本文设计的5阶模拟分解滤波器，定义D(s)=s5+as4+bs3+cs2+ds+e。则其中一路模拟分解滤波器的幅频响应可表示为

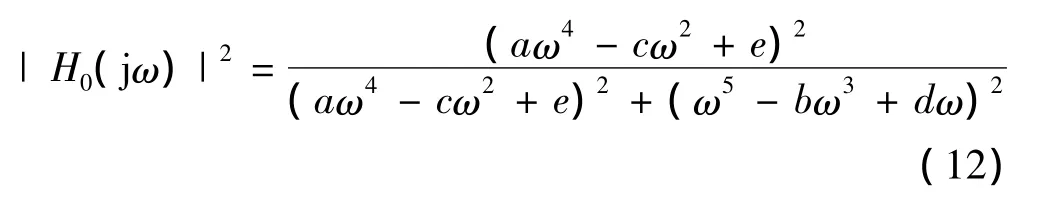
为进一步简化分解滤波器的传递函数，对其模拟滤波器的幅度值做出合理的约束，令滤波器幅频响应满足

由式(13)可推导出分解滤波器传递函数的代数关系，可用 a，b，e来表示 c，d，如式(14)所示

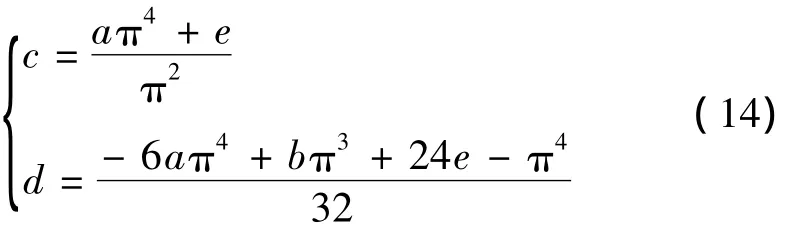
定义

同时，在分解滤波器的优化设计中，应使分解滤波器的幅频响应满足在0≤ω≤π为一平滑的曲线。则通过式(15)可表现为:f1(ω)和f2(ω)在0≤ω≤π满足相应单调性质的要求。通过数学运算简化，可将要求具体表示为代数不等式，如下所示

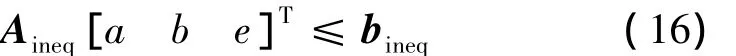
式中:Aineq为3×3的矩阵;bineq为3×1的列向量。

在应用遗传算法优化解决实际问题的时候，首要是初始设置好种群适应度评价函数。根据模拟分解滤波器组的优化设计因素，再根据式(16)的约束滤波器传递函数的系数的取值范围。依据前面所述，可得出模拟分解滤波器的优化目标函数

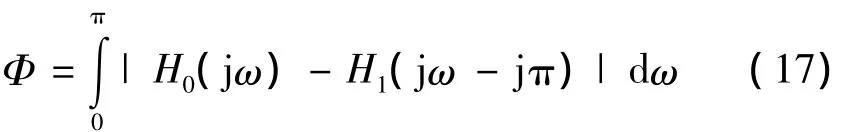
式(17)则为遗传算法的适应度评价函数，适应度评价函数只存在a、b、e三个独立变量，而后可多次应用遗传算法［8］比较得出最优的系数解，最终得到目标函数的极小值4.16E-6。应用遗传算法优化设计得到的模拟分解滤波器系统传递函数的系数为:a=1.947 1，b=69.084 8，c=141.009 8，d=566.845 1，e=4 385.449 8。

两路分解滤波器的幅频响应如图2所示，功率互补结构分解滤波器组的特性可由式(7)表现出来，也可如图3所示，可以得出基于遗传算法优化设计的分解滤波器组符合功率互补特性的结论。

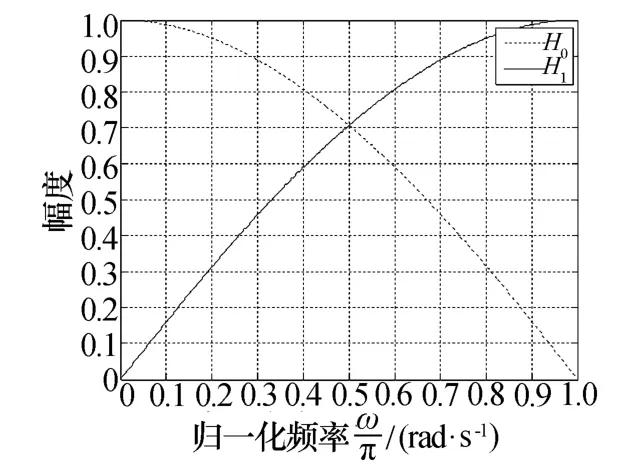
图2 优化设计的5阶模拟分解滤波器的幅频响应

1.4 数字综合滤波器的设计

对于上节已经优化设计得到的模拟分解滤波器，可以通过式(4)、式(5)得到数字综合滤波器的频率响应，利用逆快速傅里叶变换的算法设计N阶数字综合滤波器［9］。在允许一定误差的情况下对 FIR数字综合滤波器的长度进行截取，通常采用长度为L的矩形窗，矩形窗表达式如下

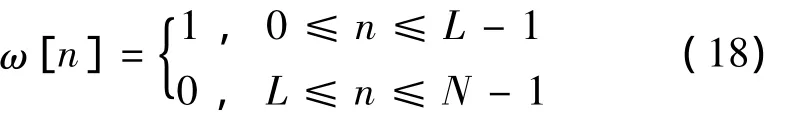
图3 功率互补结构分解滤波器组特性

那么通过加窗后的数字综合滤波器的截取系数为

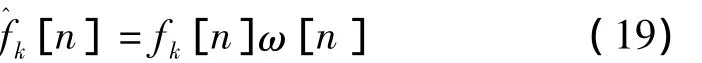
在实际数字滤波器组的优化设计中，还需要对HFB ADC系统中延时进行优化，以得到最佳延时d，使得失真函数逼近纯延时，在确定了滤波器的长度L后，HFB ADC系统的最佳延时d为L/2。

2 仿真结果

应用上述优化设计方法，设计了双通道5阶功率互补的模拟分解滤波器，32阶的数字综合滤波器，其中，系统延时，d=16。经过仿真后得到的混合滤波器组的最大失真误差为4.761 8×1011dB，最大混叠误差为-154.563 4 dB;平均失真误差为-9.268 3×10-14dB，平均混叠误差为-200.537 8 dB。混合滤波器组的失真误差和混叠误差幅度如图4、图5所示。

图4 混合滤波器组的失真误差

图5 混合滤波器组的混叠误差

如图4、图5所示，利用遗传算法优化的功率互补的5阶模拟分解滤波器在低频段也同样很好的误差特性。利用本文方法设计的混合滤波器组和现有其他方法设计的混合滤波器组［10］的系统误差比较如表1所示。

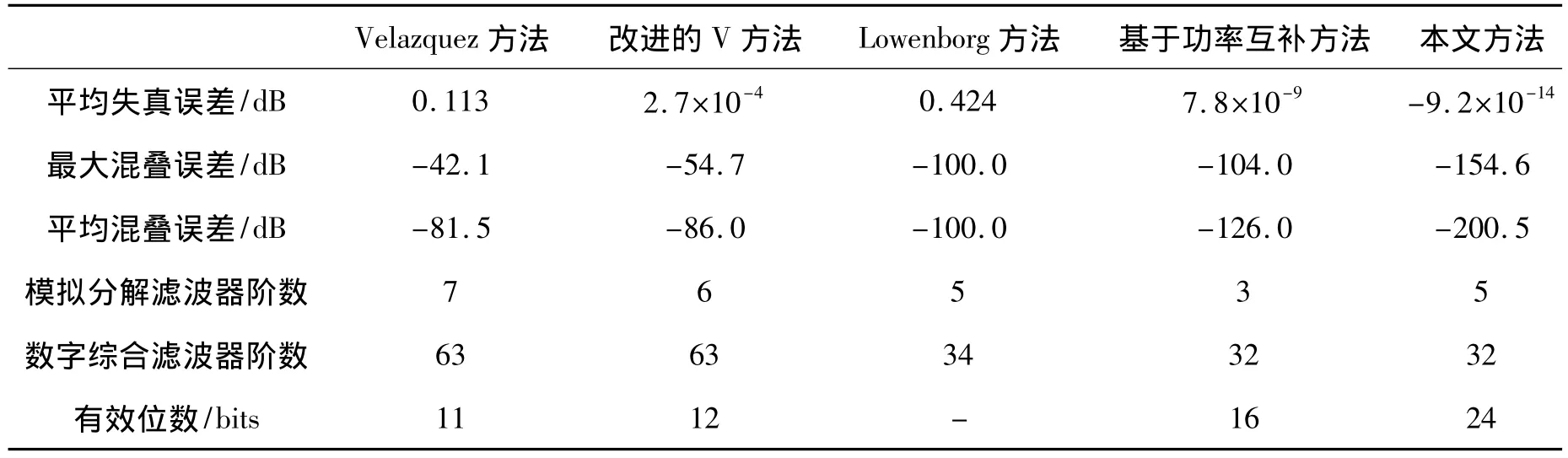
表1 混合滤波器组方法设计的比较

3 结束语

在基于混合滤波器组的数据采集系统中，本文针对模拟滤波器系数的约束条件，提出了基于遗传算法的优化方法设计来实现高阶模拟分解滤波器。实验仿真表明，相比其他方法，采用本文方法优化设计的混合滤波器组在失真误差和混叠误差方面表现出了更好的性能，可以有效提高数据采集系统的采样精度和采样速度，可以满足24 bits的ADC系统的需要，而且整个系统对模拟偏差的敏感度有了很大的降低。

［1］Velazques S R，Nguyen T Q，Broadsto S R.A hybrid filter bank approach to analog-to-digital conversion［C］//Proceedings of the IEEE-SP International Symposium on Time-Frequency and Time-Scale Analysis.［S.l.］:IEEE Press，1994:116-119.

［2］Velazques S R，Nguyen T Q.Design of hybrid filter banks for analog/digital conversion［J］.IEEE Transactions on Signal Processing，1998，46(4):956-967.

［3］Lowenborg P，Johnsson H，Wanhammar L.A design procedure for two-channel mixed analog and digital filter banks for A/D conversion using minimax optimization［C］//IEEE International Conference on Electronic Circuits System.Cyprus:IEEE Press，1999:1189-1192.

［4］Lowenborg P，Johnsson H，Wanhammar L.Two-channel digital and hybrid analog/digital multirate filter banks with very low-complexity analysis or synthesis filter［J］.IEEE Transactions on Ciruits and Systems II:Analog and Digital Signal Processing，2003，50(7):335-367.

［5］Lowenborg P.On the frequency response of M-channel mixed analog and digital maximally decimated filter banks［C］//European Conference on Circuit Theory Design.Stresa:ECCTD Press，1999:545-549.

［6］Song Q，Zhang Z J，Wang W.Design of two-channel hybrid filter banks based on power-complementary structure［C］//2011 IEEE 4th International Symposium on Microwave，Antenna，Propagation，and EMC Technologies for Wireless Communications(MAPE).Beijing，China:IEEE Press，2011:351-354.

［7］刘治宇，林茂六.一种基于功率互补对的混合滤波器组的设计［J］.西安交通大学学报，2005，39(4):389-392，397.Liu Zhiyu，Lin Maoliu.Hybrid filter banks design based on power complementary pair［J］.Journal of Xi'an Jiaotong U-niversity，2005，39(4):389-392，397.

［8］徐 璟，何明浩，冒 燕，等.基于优化算法的雷达辐射源信号识别方法及性能［J］.现代雷达，2014，36(10):33-37，42.Xu Jing，He Minghao，Mao Yan，et al.Radar emitter recognition method based on optimization algorithm and performance［J］.Modern Radar，2014，36(10):33-37，42.

［9］Cheng J，Liu W Y，Ma H.Hybrid filter banks optimization design using total least square solving［C］//2008 International Conference on Microwave and Millimeter Wave Technology.Nanjing，China:IEEE Press，2008:1960-1963.

［10］汤宁生.功率互补性混合滤波器组的设计［D］.成都:电子科技大学，2007.Tang Ningsheng.Hybrid filter banks design based on power complementary［D］.Chengdu:University of Electronic Science and Technology of China，2007.