一种新的三角贝齐尔曲面绘制方法
刘志平,曾燕璋
(淮海工学院 理学院,江苏 连云港 222005)
在计算机图形学和计算机辅助几何设计领域,经常会用到四边贝齐尔曲面和三角贝齐尔曲面,在一些实用的计算机图形系统中,两种形式的曲面会同时存在.究其原因,是因为一般现实问题的参数域通常是复杂形状,而对复杂形状的处理方法一般是将参数域剖分为小的三角形或者四边形,因此这就需要研究三角贝齐尔曲面和四边贝齐尔曲面的绘制方法.四边贝齐尔曲面实际上是两个方向的贝齐尔曲线做张量积,容易用矩阵形式表示,绘制方法相对容易.而三角贝齐尔曲面本身不具备矩阵的表示形式,绘制方法要比四边贝齐尔曲面困难,因此研究三角贝齐尔曲面的绘制方法就更有价值.
首先给四边贝齐尔曲面和三角贝齐尔曲面的定义,两种形式的贝齐尔曲面都是由控制顶点唯一确定的.
定义1[1]给定(n+1)×(m+1)个控制顶点Pi,j,i=0,1,2,…,n; j=0,1,2,…,m,n×m次四边贝齐尔曲面定义为

定义2[1]给定个控制顶点Pi,j,ki=0,1,…n; j=0,1,…n-i; k=n-i-j,n次三角贝齐尔曲面定义为

1 传统绘制方法介绍
当参数域是四边形时,采用四边贝齐尔曲面,为了方便程序实现,公式(1)经常表示成矩阵乘积的形式[2]

其中UT=[1 u u2… un],VT=[1 v v2… vm],M是从伯恩斯坦基到多项式基的转换矩阵,P是控制顶点阵.
当参数域为三角形的时候,一般采用三角贝齐尔曲面形式.比较常见的三角贝齐尔曲面绘制方法是把三角形看成退化的四边形,即四边形的一条边退化为一个点,这样三角贝齐尔曲面就变成有一条退化边的四边贝齐尔曲面[3].具体来说,如果原来的三角贝齐尔曲面的控制顶点为

为了将其表示为四边贝齐尔曲面,上述控制顶点要修改为

即添加了很多重复的控制顶点,但是从绘制结果来看,这种绘制方法并不理想,如图1所示,图形的右下角很多条线汇聚在一起,形成数据冗余,影响绘制效果.
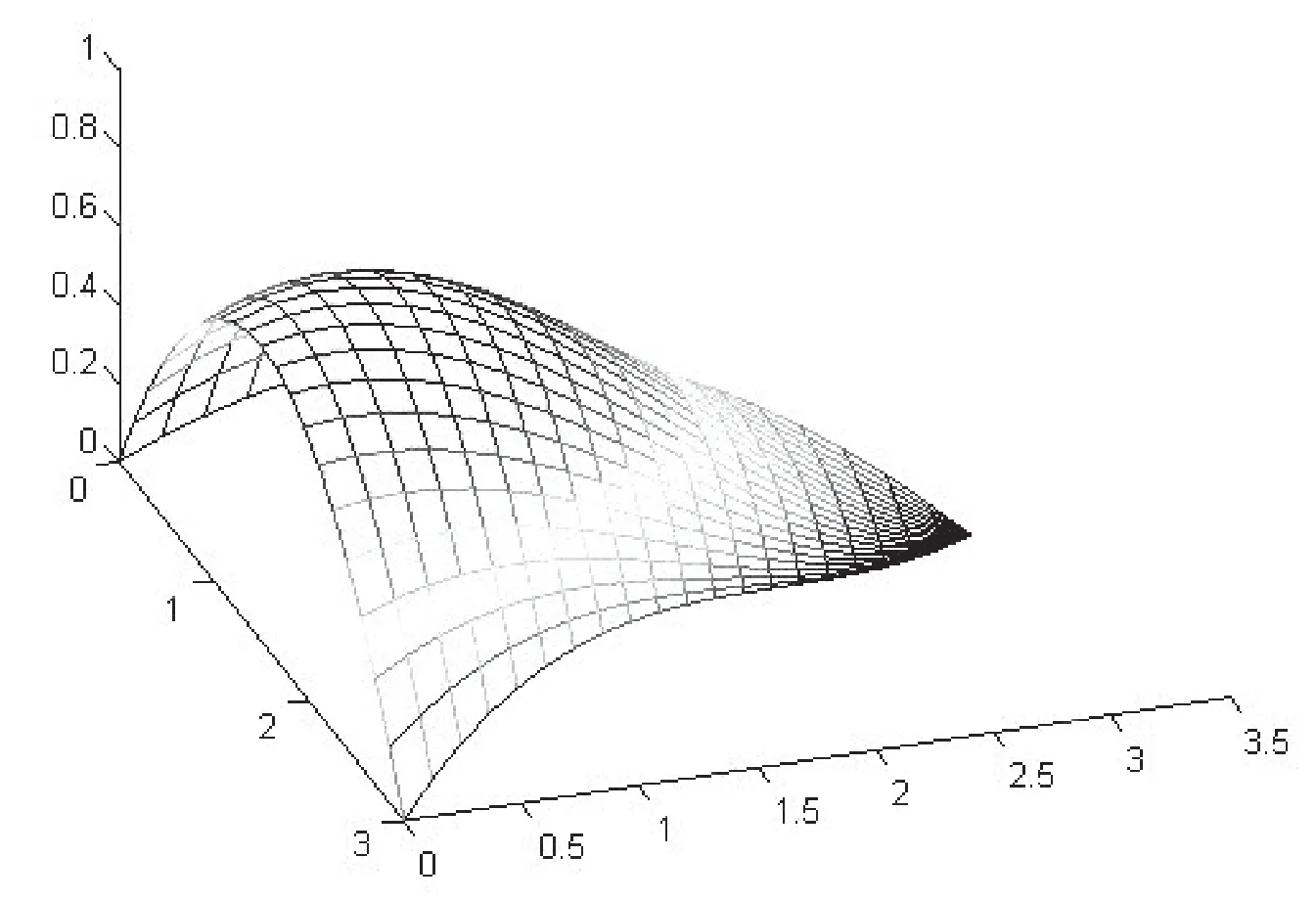
图1 将三角贝齐尔曲面看成退化的四边贝齐尔曲面
2 本文绘制方法
为了解决数据冗余的问题,三角贝齐尔曲面也可以采用Delauny三角剖分形式进行绘制,Delauny剖分的缺点是数据结构复杂,不容易理解.那么,有没有一种简单的三角贝齐尔曲面绘制方法呢?仔细考虑四边贝齐尔曲面的绘制过程,发现虽然有四条边,但其实质是两个不同方向的贝齐尔曲线进行交叉.三角贝齐尔曲面没有办法看成两个方向的交叉,那么它能否看成是三个方向的贝齐尔曲线进行交叉?基于这样的想法,在本文中,采用了一种新的三角贝齐尔曲面绘制方法,将三角贝齐尔曲面看成是三簇贝齐尔曲线的交叉,即u-向贝齐尔曲线,v-向贝齐尔曲线和w-向贝齐尔曲线的交叉.如图2所示,绘制过程中的难点是点的连接关系,下面将详细介绍具体的绘制过程.

图2 三角贝齐尔曲面参数域示意图
图2所示的三角贝齐尔曲面是3次的,现实问题里,可能需要考虑绘制任意次数的贝齐尔曲面.假定次数为n,可以看到,第一行有1个控制顶点,第二行有2个,……,如此类推.因为n次三角贝齐尔曲面共有n+1行控制顶点,所以总的控制顶点个数为将控制顶点按行进行存储,即P0,n,0的存储序号为1,P0,n-1,1的存储序号为2,P1,n-1,0的存储序号为3,…….由等差数列的性质可得,第i 行的存储序号为由此可以得到三簇贝齐尔曲线的连接关系.
首先,考虑u-向的第i 行贝齐尔曲线,其控制顶点的存储序号为

其次,考虑v-向贝齐尔曲线,最右边的v-向贝齐尔曲线其控制顶点的存储序号为
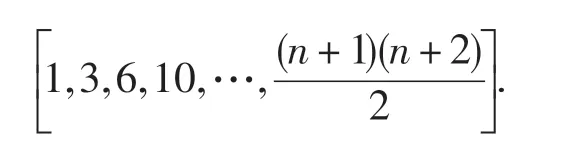
从右上方往左下方进行,每进行一次,去掉最左边的存储序号,其它序号各自减1,即第2条v-向贝齐尔控制顶点的存储序号为第3条控制顶点的存储序号为最后一条v-向贝齐尔的存储序号为
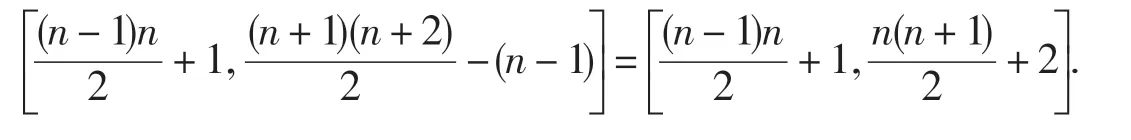
最后考虑w-向贝齐尔曲线,最左边的w-向贝齐尔曲线其控制顶点的存储序号为从左上方往右下方进行,每进行一次,去掉最左边的存储序号,其它序号各自加1,即第2 条w-向贝齐尔曲线的存储序号为第3 条的存储序号为最后一条w-向贝齐尔曲线的存储序号为
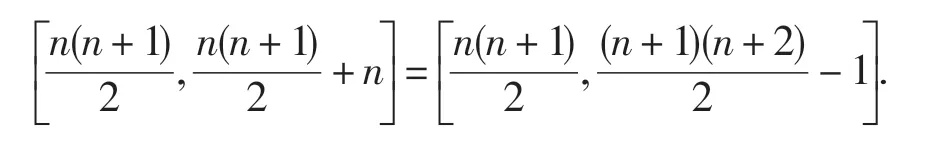
3 绘制结果
有了点的连接关系,就可以使用画折线函数分别绘制三簇不同方向的贝齐尔曲线,它们再进行交叉就会得到最终的三角贝齐尔曲面.本文中,使用MATLAB软件采用上面的方法进行了绘制,绘制结果如图3和图4所示.图3和图4是同一个曲面从两个不同方向观察到的结果,从中可以清晰地看到,已经不存在数据冗余,绘制效果良好.
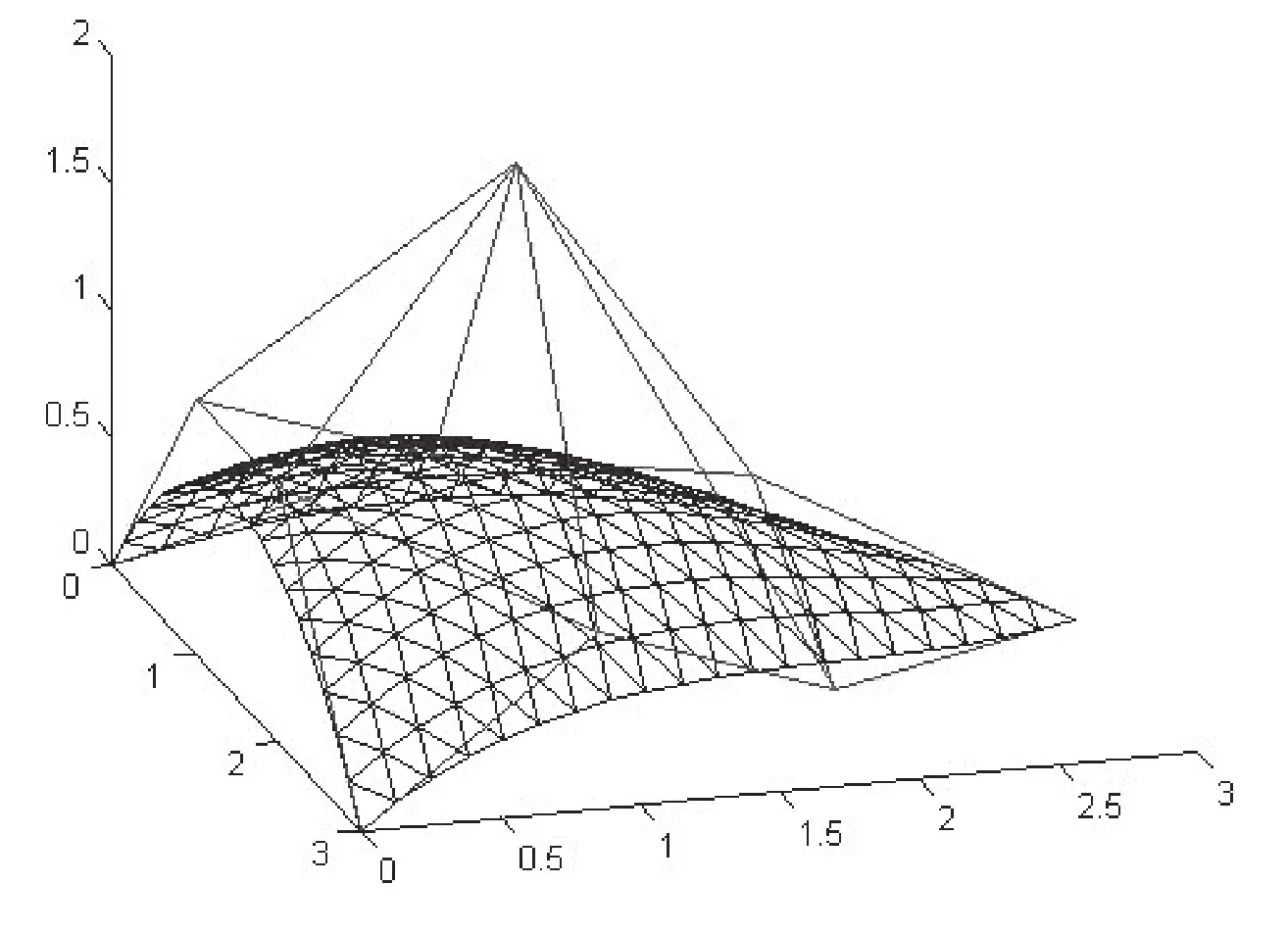
图3 采用本文方法绘制的三角贝齐尔曲面

图4 从不同角度观察图3的结果
4 结论
本文根据三角贝齐尔曲面自身的特点,采用三个不同方向的贝齐尔曲线交叉形成曲面.与已有的绘制方法相比,比传统方法数据冗余少,绘制效果好.此外,本文的方法比采用Delauny三角剖分方法更容易理解.
[1]施法中.计算机辅助几何设计和非均匀有理B样条[M].北京:高等教育出版社,2001.
[2]FARIN G.Curves and Surface for CAGD:A Practical Guide[M].San Diego:Academic Press,2002.
[3]HU Shi-min.Conversion between triangluar and rectangular Bezier patches [J].Computer Aided Geometry Desigin,2001,18(7):667-671.

