图像与中学物理概念规律的教学
一、背景和问题的提出
长期以来,我国中学物理教学一直强调概念规律及其应用,而不太重视图像的教学,物理图像只用来呈现概念规律的直观表征.在实际教学中,图像更多地被部分教师仅仅用作处理实验数据的工具,还有些教师则只关注如何利用图线更简单地解题.实践表明,学生对概念规律的理解总处于很不理想的状态;甚至相当多物理高分的或所谓学得好的学生,也并非是真正处于对概念规律的物理学理解的水平上.实质上,这已经使物理课程的学习偏离了对物理科学的学习.[1]
就物理学本身而言,图线与图像本身不仅是一种重要的物理语言,也是一种重要的研究方法[2],它与文字、公式、各类简图等物理语言相互转化,相互补充,有逻辑地把物理世界及物理量间的相应变化全面、生动地展现在我们面前.相比之下,物理图像较文字、公式更具有直观、形象的特点,更能量化地反映出多个物理量的状态变化及其相关性的特征,它能直接反映观察的结果(定性或定量的);物理图像所呈现出的对物理量变化过程的整体性描述,不仅系统而且全面.特别是,在对变化过程所具有的细节性描述以及有助于学生理解概念深层意义方面,与其他物理语言相比,堪称特色独具.
笔者认为,之所以在长期的教学中没有重视将概念规律的教学与物理图像密切结合,除了外界的原因外,许多教师对物理图像的理解和如何将物理图像用于概念规律教学两方面都缺乏思考.本文将从这一角度讨论物理图像(图线)对中学物理教学的作用.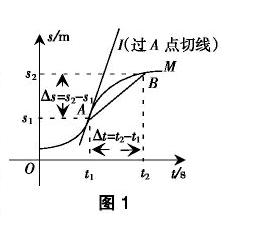
二、图像为物理概念的形成明示出一种可行方向,提供了一种思维方法
概念是关于事物本质属性及一般特征的抽象概括,它的形成需要大量相关感性材料的支撑.在需要时,个体将经验储备中相关现象的感官知觉材料,经由编码、组织、储存,从记忆中提取出来.而图像是对表象材料的排序、归类与整理后的整体图景反映,是对直接认知对象表象的条理化,是结合已有观念作出的对事物总体特征的描绘.两者都是为进一步抽象概括材料准备的认知内容.由于图像是对研究现象或过程的秩序整理,显示的是整体特征,于是从资料呈现的完整角度而言,物理图像对物理概念的形成指出了一个明确的方向.又由于图像直接表征的是物理量间的变化,借助数学知识,探究变化中隐含着的不变因素;在某种层次上说,不变是一种特征,表明一种本质——这就是概念所要表征与描述的内容;或者说就是需要引入或产生的那个概念.于是从这种意义上说,图像提供了概括抽象事物本质的一种思维活动方法.
例如加速度概念的学习.学生对生活中直线运动的物体运动速度在不断地变化是有零散但丰富的经验储备,对摩托车与小轿车的启动阶段的速度变化差异亦有着真切的认知表象.因此给出两车启动开始一段时间内一系列时刻的速度值,让学生进行比较研究是符合学生的认知的.若将两车的速度变化利用给出的数据用速度-时间图像表示出来,让学生直观地看到每一辆车运动变化的特点,在变中寻找不变,学生可发现:速度与时间都在变化,但速度变化与所用时间的比值、单位时间内的速度变化、速度的变化率等都是不变的,即速度图线的斜率等都是不变的.进一步,引导学生由图像表现出的两车速度图线的斜率不同,实质就是两车运动本质的不同——速度的变化率不同,就自然地成为我们需要引入的新概念:加速度.
又如,电场强度概念的引入,利用检验电荷的相应测量数据,实验得出:放入电场中某点的检验电荷电量变化,其受到的电场力也随之变化. 但检验电荷受到的电场力与检验电荷的电量图像是一条过原点的直线. 由于直线的斜率不变,直接得出电场力与电量的比值不变,体现出电场在该点力的本质特征. 而在电场中的不同点,力与电量的比值一般又不相同. 可见,这一比值反应了电场力的本质特征在不同点的不同——“场力”的强弱不同,电场强度不同.
三、图像提供的直观的情境,为理解物理概念搭建了一个符合认知规律的平台
(一)借助图像的直观特点,深化理解相关物理概念间的相互关联
中学生还处于经验型抽象思维的阶段,对抽象内容的理解往往需要直观内容的支持.显然,相对概念来说,图像是直观的.因此,教学的关键就在于要引导学生将二者联系起来.例如在各种复杂的直线运动中,可利用位移图像对各种速度概念(用文字与数学式描述的)加以认识上的深化.如图1所示,物体运动的s-t图像中的曲线M,分析t1至t2这段时间内物体的运动,公式定义的平均速度在这里得到了直观的诠释:直线AB的斜率.若t2逐渐向t1靠近,对应直线AB斜率的变化昭示着所分析的时间段内相对应的平均速度不同,当t2无限地趋向于t1时,公式的物理意义是物体在t1时刻的即时速度,就是图像在A点处的切线l的斜率.可见平均速度及其变化以及即时速度与平均速度的关系,在这里得到了逼真的动态直观性演示.
同样,利用图2与图3所示的v-t图像可从以下四个方面深化理解加速度:只有速度图线是不与两轴平行的直线时,它表示的运动才是匀变速直线运动;图2中的速度图线是直线,直线的斜率为该段匀变速直线运动的加速度;由于斜率为正,加速度方向与运动方向相同,物体做匀加速直线运动;图3中速度图像直线的斜率为负,该段匀变速直线运动的加速度方向与物体的运动方向相反,物体做匀减速直线运动.
此外,当速度图线是曲线时,对该图线表述的运动只能计算平均加速度.如图4所示,速度图线在某时刻切线的斜率表征着该位置时刻的瞬时加速度,即t2时刻的加速度即为曲线在该处的切线斜率,由于加速度为正,物体t1到t2时间段做的是加速运动.利用这些速度图像还可以方便地解决初学者由于运动认知材料积累不足带来的对相应运动产生的理解困难.例如,图3中的t1时刻物体的速度为零,但加速度不为零;图4是加速度逐渐减小的加速运动;图5物体做加速度逐渐增大的减速运动,等等.endprint
(二)借助对图线间关系的分析,理解复杂运动中的相关概念
对描述多体复杂运动的物理概念,教学中遇到的困难多是由于学生缺少对相关运动的认知经历,对运动发生的过程及其特点没有形成对应的想象储备.例如因波源与观察者相对运动而使观察者接收到的波频率发生改变的多普勒效应现象.对此现象理解的支持是,想象出波源与观察者之间有相对运动时,观察者接收到波的周期(频率)会发生何样的变化呢?对学生的想象困难,可用位移图像给予直观支撑.设波在介质中直线匀速传播速度为v0,波的振动周期为 T.简单地,分析波源静止、观察者相对波源运动的情况.先对静止的观察者而言,若只关注波动的特殊状态(比如波峰),将看到从波源位置处每隔时间 T就有一个波峰状态以速度v0匀速向外传播.若观察者再以速度v向波源方向匀速靠近,各对象的运动位移图像将如图6所示.
由图6,观察者接收到的波峰1与波峰2的时间间隔DB自然小于波源发出两峰的时间间隔CB.即观察者在此运动状态下接收到波的周期小于波源振动周期.直观可见多普勒效应是物体由于相对运动而出现的不同参考系中观察到的同一事件发生时间间隔不同的一种自然结果.进一步,还可利用图线形状呈现出的几何关系,计算出频率变化的数量关系.
观察者接收到两个波峰信号时间间隔t的值可由下求出:
在△ACD和△ABD中,有
CD×tanα=DB×tanβ,(T-t)v0=tv得,t=T.
频率为f0=波动信号(以波源连续发出波的两个波峰为标志).在波传播方向的直线上,以速度v向波源运动的观察者接收到波的频率f=将发生改变,且结果为:
∵t=T,∴f=(1+)f0.
四、通过图像中物理量的变化读出概念的深层次物理意义,为发现新概念提供了直观的依据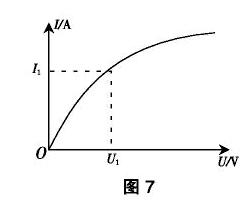
(一)从图像中物理量的变化读出概念的深层次物理意义
由于图像中呈现出的连续性曲线,是对过程中相应物理量的细节性描述,由此便可以引导学生理解概念的深层次意义.例如匀速运动的v-t图线,利用平面内坐标点可描述物体在某一个时刻的速度;于是可帮助学生理解:速度乃是描述物体运动状态而非运动过程的物理量,速度随时间的推移就可描述一个运动的过程;进而,物理学中说的匀速运动则一定是个理想过程,因为在任一时刻都具有相等速率的运动在实际中并不存在.又如从小灯泡的U-I图线,如图7所示.所给出的关于小灯泡灯丝材料的电阻信息,不但比直接用文字语言表述或数据列表等方法梳理出灯丝电阻要简单得多,而且特别值得注意的是,该图线所揭示出的“冷灯丝电阻随温度呈现的动态变化”几乎是用语言与公式分析难于发现的.
(二)为发现新概念提供了直观的依据
在光电效应现象的研究中,实验得出的光电子的最大初动能,与入射光的频率关系图像,如图8所示.不仅使我们感受到了光电子的最大初动能与光的强度无关(光子个数),是与光的频率线性相关的粒子性行为.由直线与横轴的交点位置,更使我们认识到极限频率概念的存在及其意义.
研究等压条件下,一定质量的理想气体的体积随温度变化的情形,利用描点法画出实验得到的等压线如图9,图线并未通过原点表明0℃时气体的体积并不等于零这一事实.直线反向延长交t轴于d点,得到t1=-273℃,从而外推到零体积,产生了理想气体温标,定义出了绝对零度这一“极限”概念,并明确了它的物理意义.
五、图像为概念间的联系积累材料,丰富了物理规律建立的途径
概念是规律的基础,规律反映了概念间的联系;但是学生对这一点的理解通常依靠对错题原因的反思来实现.实际上,从实验物理走进理论物理,规律的建立方法已发生了根本的改变.在中学物理教学中,如果借助不同图线间的物理关系来建立规律,则可以在一定程度上对这一方法的变化提供隐喻性的支持.
例如,通过对合外力与时间的曲线及加速度与时间的曲线的综合分析来推导动量定理.设质量为 m的物体做直线运动,其受到的变化的合力F随时间的变化如图10所示,该物体运动的加速度随时间的变化图像如图11所示.由牛顿第二定律可知,图11只是图10中每一相同时刻的对应点的纵坐标值与m之比所形成的图形;即图11中曲线与横轴所围面积的m倍应与图10中曲线与横轴所围面积相等,这一点可以通过方格法计算两个面积验证.由图像的物理意义可知,图10中曲线与横轴所围面积表示力在时间 t内的冲量I;图11中曲线与横轴所围成的面积表示时间t内物体速度的增量Δv.若物体时间t=0时刻速度为v0,t时刻速度为vt,则Δv=vt-v0 ,比较两幅图形有:I=mΔv=mvt-mv0.
对动量定理进行这样有“直观证据”支撑的认识,不仅促进了对概念规律的真理解,还会潜移默化地为具体问题的解决找到新的途径,形成新的方法.
参考文献:
[1] 马广明. 加强物理图像教学 提高对概念规律的学习效率[J]. 物理教师,2014(11).
[2] 袁丽. 中学物理课程中数学知识的支持性研究[D]. 重庆:西南大学,2009.
[3] 阎金铎,段金梅,续佩君,等. 物理教学论[M]. 南京:江苏教育出版社,1990.endprint

