多值线性算子的正则Fredholm对的子空间序列

范亚静，蹇人宜

（1北方民族大学 数学与信息科学学院，宁夏 银川750021；2陕西师范大学 数学与信息科学学院，陕西 西安710119）

多值线性算子 （又称线性关系）是线性算子概念的自然推广。最重要且最简单的例子是从线性空间X到线性空间Y的线性算子T的逆象，即解的集合T－1y：＝｛x∈X：Tx＝y｝，∀y∈Y。多值线性算子的概念产生于20世纪50年代von Neumann关于非稠定线性微分算子的共轭算子的研究［1］。此后，最优化与控制论的研究引出了对多值线性算子的研究［2－3］。多值线性算子的理论和方法也用来处理偏微分方程［4］和常微分方程［5］的某些问题。线性算子的Fredholm理论在应用数学中是一个十分有用的工具。Cross将经典的Fredholm理论移植到线性关系中，获得了一系列十分有价值的结果［7－11］。Alvarez在文献［12］中还考虑了赋范空间中的几乎半－Fredholm线性关系。与此同时，Fredholm算子及指标的概念也以多种不同的方式，向多个算子方向发展。Banach空间的Fredholm复形、Fredholm算子对及相应指标的稳定性已有许多研究。此外，Boasso在文献［13］中讨论了正则的Fredholm对及其分类。本文将单值线性算子的正则Fredholm对的研究思想推广到多值线性算子的范畴中，引入了Banach空间X、Y上的多值线性算子S、T构成的正则Fredholm对的概念及其相应的子空间序列（RS，n）n∈N、（RT，n）n∈N、（RS，n）n∈N＋和（RT，n）n∈N＋并给出其性质。

1 基本概念与记号

定义1［6］设U、V…是任意非空集合，关系T是从U到V的映射，其定义域是U的子集D（T），且取值于2V＼∅。从U到V的全体关系记为R（U，V）。

定义2［6］设X、Y是数域K＝R或C上的向量空间，关系T∈R（X，Y）称为线性关系（或多值线性算子），是指对于所有的x、z∈D（T）以及非零系数α∈K，有

（1）Tx＋Tz＝T（x＋z）；

（2）αTx＝T（αx）。

定义3［6］记LR（X，Y）为从线性空间X到线性空间Y所有线性关系构成的集合。T（X）＝T（D（T））称为T的值域｛x∈D（T）：0∈Tx｝称为T的核x∈X，y∈Tx｝称为T的图像。

定义4［6］设X、Y为Banach空间，若G（T）为X×Y中的闭集，则称T为闭关系。

设X、Y为Banach空间，用记号BR（X，Y）表示X到Y的有界线性关系构成的集合。这意味着‖T‖==d‖QT‖＜∞，其中Q＝QT是以X为定义域，以为零空间的自然商映射。

定义5［6］S∈BR（X，Y）叫作Fredholm关系，是指S是闭的，且满足下列三个条件：

（Ⅰ）R（S）闭；

（Ⅱ）dim N（S）＜∞；

（Ⅲ）codimR（S）＜∞。

记F＝F（X，Y）表示所有LR（X，Y）上的Fredholm关系构成的集合。

定义6［14］设S∈BR（X，Y），T∈BR（Y，X），且S、T是闭的，使得

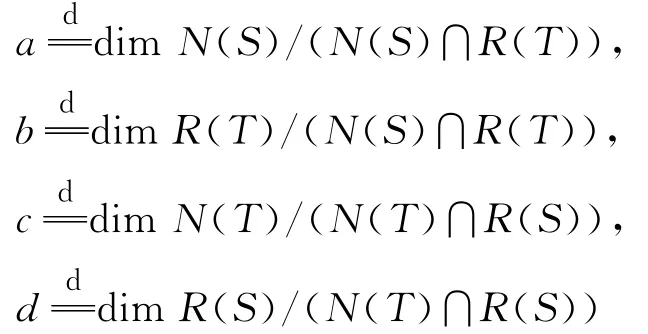
是有限的，则（S，T）称为多值线性算子的Fredholm对，记为（S，T）∈PR（X，Y）。

若T∈LR（X，Y）称为正则的，是指T是闭的，且存在闭的T′∈LR（Y，X），使得T＝TT′T。又若（S，T）∈PR（X，Y），且S、T均是正则的，则称（S，T）是正则Fredholm对，记为（S，T）∈RPR（X，Y）。

命题1 如果（S，T）∈RPR（X，Y），那么下述论断等价：

（Ⅰ）R（T）是X的可补子空间；

（Ⅱ）N（S）是X的可补子空间；

（Ⅲ）N（S）＋R（T）是X的可补子空间；

（Ⅳ）N（S）∩R（T）是X的可补子空间；

（Ⅴ）R（S）是Y的可补子空间；

（Ⅵ）N（T）是Y的可补子空间；

（Ⅶ）N（T）＋R（S）是Y的可补子空间；

（Ⅷ）N（T）∩R（S）是Y的可补子空间。

本文延续文献［14］的内容，进一步讨论多值线性算子的正则Fredholm对的子空间序列（RS，n）n∈N、（RT，n）n∈N、（RS，n）n∈N＋和（RT，n）n∈N＋的一些性质。通过分析可知，其均为递减的，从而有类似于文献［13］的分解。

2 子空间序列（RS，n）n∈N、（RT，n）n∈N

定义7 设X、Y是两个Banach空间，（S，T）∈RPR（X，Y），子空间序列（RS，n）n∈N和（RT，n）n∈N分别递归地定义为RS，0＝Y，RT，0＝X，若RS，n、RT，n已定义，则RS，n＋1==dS（RT，n），RT，n＋1==dT（RS，n），这里N是包括0的自然数集。

命题2 （RS，n）n∈N、（RT，n）n∈N分别是Y、X的递减序列。若S（0）、T（0）是有限维的，则RS，n、RT，n是Y和X的有限维子空间，∀n≥2。

证明 RS，1＝S（RT，0）＝S（X）＝R（S）⊆Y＝RS，0；RT，1＝T（RS，0）＝T（Y）＝R（T）⊆X＝RT，0。

假定RS，n⊆RS，n－1，RT，n⊆RT，n－1对于n≥1成立，则

RS，n＋1＝S（RT，n）⊆S（RT，n－1）＝RS，n；

RT，n＋1＝T（RS，n）⊆T（RS，n－1）＝RT，n。又因为

RS，2＝R（ST）≅R（T）／（N（S）∩R（T））S（0），所以RS，2是有限维的。由于RS，n⊆RS，2，因此RS，n（n≥2）是有限维的。

同理，RT，n（n≥2）也是有限维的。

命题3 设X、Y是Banach空间，设（S，T）∈RPR（X，Y），则对任何给定的n∈N＋（这里N＋表示正整数集），分别有X的子空间Nn、Xn2，Y的子空间Mn、Yn2，使得

（Ⅰ）RS，n＝Mn⊕Yn2，RT，n＝Nn⊕Xn2；

（Ⅱ）Mn＝RS，n∩N（T），Nn＝RT，n∩N（S）；

（Ⅲ）Yn2＝RS，n∩Yk2，Xn2＝RT，n∩Xk2，k＝1，2，…，n－1；

（Ⅳ）（Mn）n∈N＋和（Nn）n∈N＋分别是包含于N（T）和N（S）的子空间下降序列，若S（0）、T（0）是有限维的，则（Mn）n∈N＋、（Nn）n∈N＋是有限维子空间序列；

（Ⅴ）（Yn2）n∈N＋、（Xn2）n∈N＋分别是Y2、X2的子空间下降序列，若S（0）、T（0）是有限维的，则（Yn2）n∈N＋、（Xn2）n∈N＋是有限维子空间序列；

证明 定义M1==dN（T）∩R（S），X12==dX2，N1==dN（S）∩R（T），Y12==dY2。按照文献［14］注2．8的（Ⅱ）和（Ⅲ），得到命题3的（Ⅰ）和（Ⅱ）。

假设命题对于n≥1时成立，则由（Ⅵ）有，S（或T）可诱导出拟同构RT，n＋1），那么PSS：⊖S（0）（或PTT：T（0））是同构算子。

由文献［14］注2．17知，T、S可分别诱导出拟同构

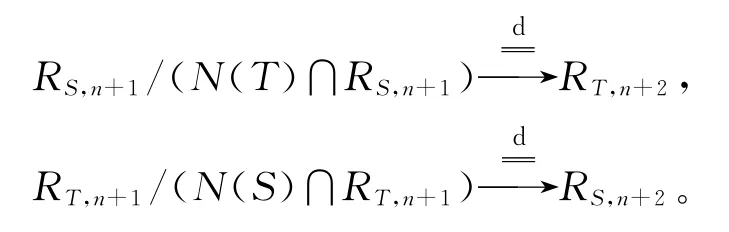
故分别有Y和X的子空间V和W，使得

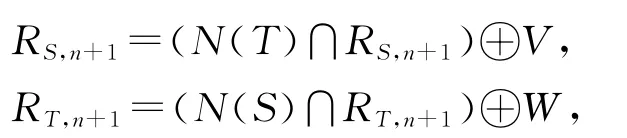
选择V⊆Yn2，W⊆Xn2，并定义

因此｛Yn2｝n∈N、｛Xn2｝n∈N分别是包含在Y2、X2中的下降序列。（Ⅴ）成立。（Ⅵ）、（Ⅱ）是显然的。又

RS，n＋1＝Mn＋1⊕Yn＋12，RT，n＋1＝Nn＋1⊕Xn＋12，即（Ⅰ）成立。

由定义有

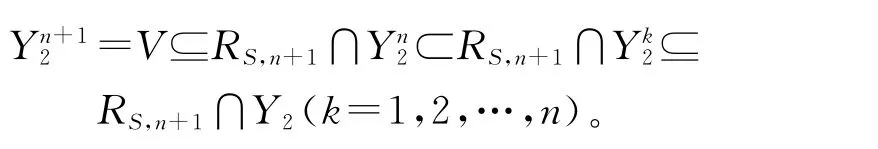
另一方面，∀a∈RS，n＋1∩Y2，因为RS，n＋1＝（N（T）∩RS，n＋1）⊕Yn＋12，所以存在唯一的m∈N（T）∩RS，n＋1，y∈Yn＋12，使得a＝m＋y，从而m∈N（T），y∈Yn＋12⊂Y2。又由a－y∈Y2，即m∈Y2，可知m∈N（T）∩Y2，则m＝0。因此a＝y∈Yn＋12。这样便得到Yn＋12⊆RS，n＋1∩Y2⊂Yn＋12。故Yn＋12＝RS，n＋1∩Yk2＝RS，n＋1∩Y2（k＝1，2，…，n）。

同理，Xn＋12＝RT，n＋1∩Xk2＝RT，n＋1∩X2（k＝1，2，…，n）。于是，Yn2＝RS，n∩Yk2，Xn2＝RT，n∩Xk2（k＝1，2，…，n－1）。

由S（0）、T（0）是有限维的，以及命题2知，RS，n、RT，n是有限维的，因此（Yn2）n∈N＋、（Xn2）n∈N＋也是有限维序列。即（Ⅲ）成立。

由（Ⅲ）知，Yn＋12＝RS，n＋1∩Y2，Yn2＝RS，n∩Y2，Yn＋12⊂Yn2，因此RS，n＋1⊂RS，n，故

Mn＋1＝N（T）∩RS，n＋1⊂N（T）∩RS，n＝Mn。于是，｛Mn｝n∈N＋是包含于N（T）的下降序列。

同理，｛Nn｝n∈N＋是包含于N（S）的下降序列。并且当S（0）、T（0）是有限维时，由命题2知，RT，n、RS，n是有限维的，于是，｛Mn｝n∈N和｛Nn｝n∈N＋是有限维的，故（Ⅳ）成立。

3 子空间序列（RS，n）n∈N＋、（RT，n）n∈N＋

定义8 设X、Y是两个Banach空间，且（S，T）∈RPR（X，Y），Y和X的子空间序列（RS，n）n∈N＋和（RT，n）n∈N＋分别定义为

RS，1＝R（S）＝S（X），RT，1＝R（T）＝T（Y），若RS，n、RT，n已经定义，则

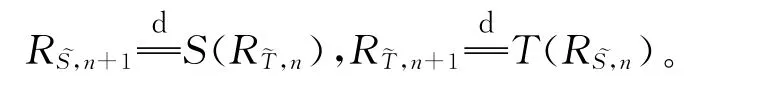
这里，X、Y、S、T是文献［14］注2．17引入的子空间和线性关系。

显然，RS，n⊆RS，n，RT，n⊆RT，n，∀n∈N＋。

关于RS，n和RT，n有如下基本事实。

命题4 设X、Y是Banach空间，设（S，T）∈RPR（X，Y），S（0）、T（0）是有限维的，则有X的子空间的两个序列（Nn）n∈N、（Xn2）n∈N＋，Y的两个子空间序列（Mn）n∈N＋、（Yn2）n∈N＋，使得∀n∈N＋，有

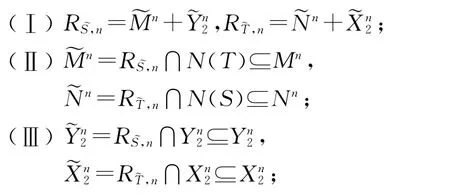
（Ⅳ）T（或S）诱导出拟同构

（Ⅴ）RS，n＝RS，n＋1＋RS，n，RT，n＝RT，n＋1＝RT，n；

（Ⅵ）Mn＝Mn＋1＋Mn，Nn＝Nn＋1＋Nn；

（Ⅶ）Yn2＝Yn＋12＋Yn2，Xn2＝Xn＋12＋Xn2；

（Ⅷ）当n＝1时，分别有X的子空间XN、X2和Y的子空间YM、Y2，使得X2、Y2是有限维的，且X＝XN＋X2，Y＝YM＋Y2，并有拟同构

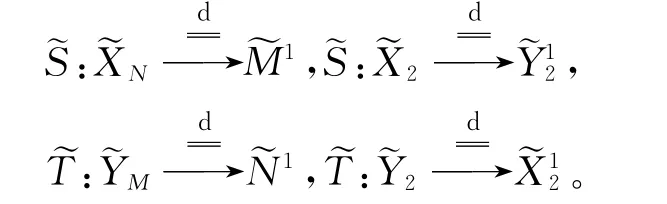
证明 ∀n∈N＋，考虑由T诱导的拟同构

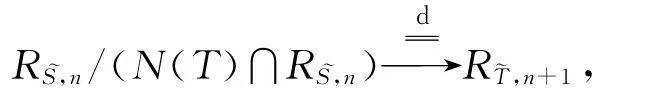
因为RT，n＋1⊆RT，n＋1⊆RT，2＝R（TS），所以存在RS，n的一个有限维子空间Ln，使得

RS，n＝（N（T）∩RS，n）＋Ln。

另一方面，∀a∈RS，n∩Yn2，∃唯一的m∈N（T）∩RS，n，l∈Ln，使得a＝m＋l。由于a∈Yn2，l∈Ln⊆Yn2，故a－l∈Yn2，又a－l＝m∈N（T）∩RS，n，因此

又由命题3（Ⅲ）知，

这里，k＝1，2，…，n－1，因而a－l＝m＝0，故a＝l∈Ln。于是RS，n∩Yn2＝Ln。定义Mn＝RS，n∩N（T），Yn2＝Ln。显然，（Ⅰ）—（Ⅳ）关于S的结论成立。

同理可得，（Ⅰ）—（Ⅳ）关于T的结论也成立。

下证（Ⅴ）。首先由文献［14］注2．17知，

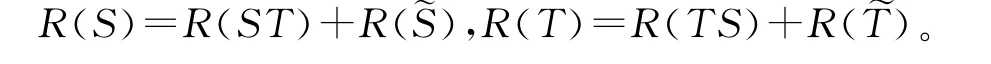
假设对于S、T当n≥1时结论成立，即有

RS，n＝RS，n＋1＋RS，n，RT，n＝RT，n＋1＋RT，n，那么由命题3（Ⅵ），并且

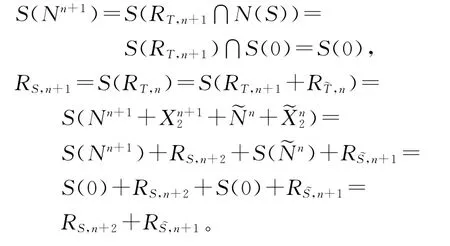
同理，RT，n＋1＝RT，n＋2＋RT，n＋1。所以（Ⅴ）对于一切n≥1都成立。

接下来证（Ⅵ）和（Ⅶ）。根据命题3（Ⅰ）及已证明的命题4（Ⅰ）和（Ⅴ）有

特别地，

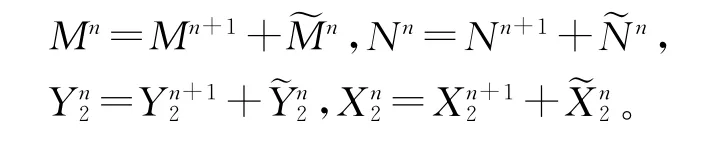
同理可得，关于T的类似结论。

注1 设X、Y是Banach空间，设（S，T）∈RPR（X，Y），对于n∈N，根据文献［14］注2．17，有

X＝R（T）＋X1＋X，Y＝R（S）＋Y1＋Y。

又根据命题3、命题4，有

同理，

这里i＝1，2，…，n－1。

［1］Von Neumann J．Functional operators［M］．Princeton：Princeton University Press，1950．

［2］Aubin J P，Cellina A．Differential inclusions［M］．Berlin：Springer－Verlag，1984．

［3］Clarke F H．Optimization and nonsmooth analysis［M］．Philadelphia：Society for Industrial and Applied Mathematics，1983．

［4］Gromov M．Partial differential relations［M］．New York：Springer－Verlag，1986．

［5］Favini A，Yagi A．Multivalued linear operators and degenerate evolution equations［J］．Annali di Matematica Pura ed Applicata，1993，163（4）：353－384．

［6］Cross R W．Multivalued linear operators［M］．New York：Marcel Debber Inc，1998．

［7］Cross R W．An index theorem for the product of linear relations［J］．Linear Algebra and its Applications，1998，277（1）：127－134．

［8］Cross R W．Essential state diagrams for closed linear relations［C］∥Dimitǔr Baǐnov．Proceedings of the Sixth International Colloquium on Differential Equations．Plovdiv：VSP International Science Publishers，1996．

［9］Cross R W．Note on the canonical factorization of a multi－valued linear operator［J］．Communications in Applied Analysis，1999，3（4）：461－469．

［10］Cross R W，Labuschagne L E．Characterisations of operators of lower semi－Fredholm type in normed linear spaces［J］．Quaestiones Mathematicae，1992，15：151－173．

［11］Cross R W，Pillay P．Ubiquitous properties of certain operational quantities of linear relations in normed spaces［J］．Quaestiones Mathematicae，1994，17：487－498．

［12］Alvarez T．On almost semi－Fredholm linear relations in normed spaces［J］．Glasgow Mathematical Journal，2005，47：187－193．

［13］Boasso E．Regular Fredholm pairs［J］．Operator Theory，2006，55：311－337．

［14］范亚静．关于正则Fredholm多值线性算子对［J］．应用泛函分析学报，2012，14（3）：265－273．