具有双参数的非局部反应扩散方程非线性奇摄动问题

具有双参数的非局部反应扩散方程非线性奇摄动问题

许永红1， 陈贤峰2， 韩祥临3， 莫嘉琪4

(1 蚌埠学院 数理系, 安徽 蚌埠 233030; 2上海交通大学 数学系, 上海 200240;

3 湖州师范学院 理学院, 浙江 湖州 313000; 4 安徽师范大学 数学系, 安徽 芜湖 241003)

摘要：研究了一类具有两个小参数的非局部反应扩散方程奇摄动初始边值问题。在适当的条件下求出原问题的外部解,利用伸长变量、合成展开法和幂级数展开理论构造出解的初始层项和边界层项,得到形式渐近解；利用比较定理讨论了原初始边值问题解的存在性和解的一致有效的渐近展开式。

关键词:非局部; 反应扩散; 奇摄动

中图分类号：O175.29文献标志码： A

文章编号：1672-4291(2015)01-0013-06

doi:10.15983/j.cnki.jsnu.2015.01.113

收稿日期：2014-06-16

基金项目：国家自然科学基金资助项目(11271236); 中央高校基本科研业务费专项资金项目(GK201302025,

The nonlocal singularly perturbed problem for nonlinear

reaction diffusion equation with two parameters

XU Yonghong1, CHEN Xianfeng2, HAN Xianglin3, MO Jiaqi4

(1 Department of Mathematics & Physics, Bengbu College, Bengbu 233030, Anhui, China;

2 Department of Mathematics, Shanghai Jiaotong University, Shanghai 200240, China;

3 Faculty of Science,Huzhou University, Huzhou 313000, Zhejiang, China;

4 Department of Mathematics, Anhui Normal University, Wuhu 241003, Anhui, China)

Abstract:A class of nonlocal for the singularly perturbed initial boundary value problem of the reaction diffusion equation with two small parameters is considered. Under suitable conditions, the outer solution of the original problem is solved. Using the stretched variables, composing expansion method and expanding theory of power series，the terms of the initial layer and boundary layer are constructed and the formally asymptotic solution is obtained. Finally, using the comparative theorem, the existence of solution for the original problem and the uniformly valid asymptotic expansion are discussed.

Key words: nonlocal; reaction diffusion; singular perturbation

MR subject classification: 35B25

非线性问题的研究一直在国内外学术界十分活跃，各种近似方法也在不断创新[1-9]。 文献[10-23]利用微分不等式、不动点定理等理论和方法讨论了一类奇摄动非线性问题。本文用奇摄动理论来讨论一类具有双参数的非局部奇摄动反应扩散问题的渐近解。

讨论如下非局部非线性奇摄动反应扩散方程初始边值问题：

(t,x)∈(0,T0]×Ω,

(1)

u=g(t,x,ε,μ), (t,x)∈[0,T0]×∂Ω,

(2)

u=h(x,Tu,ε,μ),t=0,

(3)

其中ε、μ为正的小参数,x≡(x1,x2,…,xn)∈Ω,Ω为Rn中的有界凸域,T0为足够大的正常数,∂Ω为具有C1+α函数类的Ω的边界,α∈(0,1)为Hölder指数,L为一致椭圆型算子：

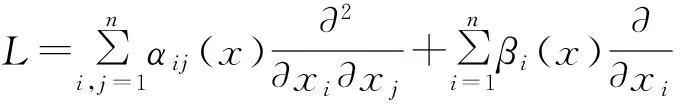
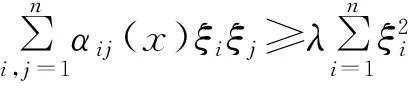
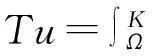
假设：

[H2]αjk、βj、a、K及其偏导数关于其变量在对应的区域内为Hölder连续的;

[H3]f(t,x,y,εTy,ε,μ)、g(t,x)、h(x,y)在对应的区域上关于t、x为Hölder连续,关于y为Lipschitz连续,关于ε、μ为充分光滑的函数，且

max(fy(t,x,y,z,ε,μ),fz(t,x,y,z,ε,μ))≤

-c1<0,

hz(x,z,ε,μ)≤-c2<0,g(0,x)|x∈Ω=h(x),

其中c1、c2为常数。

1外部解的构造

构造问题(1)—(3)解的形式渐近展开式。 问题的退化方程为

f(t,x,u,Tu,0,0)=0, (t,x)∈[0,T0]×Ω。

(4)

由假设知,积分方程(4)存在解

u=U00, (t,x)∈[0,T0]×C1+α。

(5)

设问题(1)—(3)的外部解U的展开式为

(6)

将(6)式代入(1)式,把f按ε、μ展开为双重幂级数,合并ε、μ同次幂,且分别使εi、μj同次幂的系数为零,可得

fy(t,x,U00,TU00,0,0)Uij+

fz(t,x,U00,TU00,0,0)TUij=

i、j=0,1,2,…;i+j=0。

(7)

其中，Fij(i、j=0,1,2,…;i+j≠0)为逐次已知的函数,其结构从略。设上面和下面的各式中出现负下标的项为零。由积分方程(7),可依次得到Uij(i、j=0,1,2,…;i+j≠0)。

将得到的Uij代入(6)式,可得原问题的外部解U。 但是它未必满足条件(2)和(3)式,故尚需构造初始层校正函数V和边界层校正函数W。

2初始层校正项的构造

引入伸长变量[1]:τ=t/ε,并令原问题的解u为

u=U+V。

(8)

将(8)式代入(1)和(3)式,得

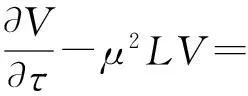
(9)

V(0,x,ε,μ)=h(x,T(U+V),ε,μ)-

U(0,TU,ε,μ),τ=0。

(10)

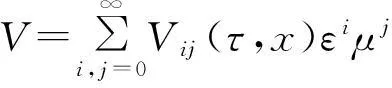
(11)

将(6)、(11)式代入问题(9)—(10),并将非线性项展开为ε、μ的双重幂级数,合并ε、μ同次幂,且分别使ε、μ同次幂的系数为零。对于ε0μ0的系数,可得

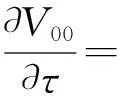
(12)

V00(0,x)=hz(x,T(U00(0,x)+V00(0,x)),0,

0)TV00-U00(0,x)。

(13)

对于εiμj(i、j=1,2,…,i+j≠0)的系数为零,有

fz(0,x,U00+V00,T(U00+V00),0,0)TVij+Gij,

(14)

Vij(0,x)=hz(x,T(U00+V00),0,0))TVij+Hij-Uij,

(15)

其中Gij、Hij(i、j=0,1,2,…,i+j≠0)为逐次已知的函数,其结构从略。

由假设知,微分方程(12)、(14)和积分方程(13)、(15)依次可得解Vij(τ,x)(i、j=0,1,2,…)。

将得到的解Vij(τ,x)(i、j=0,1,…)代入(11)式, 便得到初始层校正函数V。 但是，这时(8)式u=U+V未必满足边界条件(2), 故尚需构造边界层校正函数W。

3边界层校正项的构造

首先,在∂Ω附近邻域建立局部坐标系(ρ,φ)。定义在∂Ω附近的邻域内的每一点P的坐标ρ(≤ρ0)为点P到边界∂Ω上的距离,这里ρ0为足够小的常数,使得在边界∂Ω上的每一点的内法线在∂Ω的邻域ρ≤ρ0内互不相交。而φ=(φ1,φ2,…,φn-1)为在∂Ω上的一个非奇异坐标,点P的坐标φ为点P∂Ω的坐标φ，其中点P∂Ω为通过点P的内法线和边界∂Ω的交点。

在∂Ω的邻域ρ≤ρ0中有

(17)

其中ain、aij、bn、bi为已知函数, 其结构从略。

设原问题的解u为

u=U+V+W。

(18)

引入伸长变量

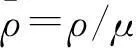
(19)

将(18)、(19)式代入问题(1)—(3),有

V+W),ε,μ)-f(ετ,ρ,φ,U+V,T(ετ,U+

V),ε,μ),

(t,ρ)∈(0,T0]×(ρ≤ρ0),

(20)

W=g(ετ,0,φ,ε,μ)-U-V,ρ=0,

(21)

W=h(0,ρ,φ,T(U+V+W),ε,μ)-U-V,

τ=0,

(22)

设

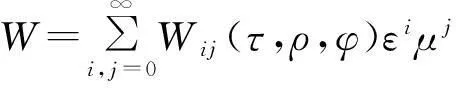
(23)

将(6)、(11)、(23)式代入问题(20)—(22)式,并将非线性项展开为ε、μ的幂级数,合并ε、μ同次幂,且分别使ε、μ同次幂的系数为零。对于ε0μ0的系数,可得

V00),0,0)W00+fz(0,0,φ,U00+V00,

T(U00+V00),0,0)TW00-f(0,0,φ,U00+

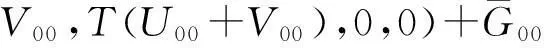
(24)

W00(t,0,φ)=g(0,0,φ,0,0)-U00(0,0,φ)-V00(0,0,φ)，

(25)

W00=hy(0,ρ,φ,T[U00+V00],0,0)W00+

hz(0,ρ,φ,T[U00+V00],0,0)TW00,τ=0。

(26)

对于εiμj(i、j=0,1,2,…,i+j≠0)的系数，依次可得

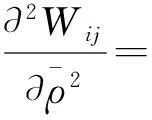
(27)

Wij(t,0,φ)=-(Uij(t,0,φ)+Vij(t,0,φ)),

(28)

(29)

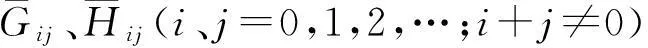
由问题(24)—(26)式和问题(27)—(29)式和假设知,能够依次得到解Wij(t,ρ,φ)(i、j=0,1,2,…)。再将其代入(23)式,便得到具有边界层校正函数W。

于是，由(18)式, 便得到非线性反应扩散方程奇摄动初始边值问题(1)—(3)解u的形式渐近展开式为

(t,x)∈(0,T0]×Ω,0<ε,μ≪1。

(30)

4解的合成展开式

现在证明(30)式为问题(1)—(3)解的一致有效的渐近展开式。

定理1在假设[H1]-[H3]下,具有两个小参数的奇摄动非线性非局部反应扩散方程初始边值问题(1)-(3)存在一个解u,并在(t,x)∈[0,T]×(Ω+∂Ω)上, 关于小参数ε、μ成立一致有效的渐近展开式(30)。

证明首先, 构造辅助函数α和β，

α=Ymn-rζ,β=Ymn+rζ,

(31)

其中ζ=max(εm+1μn,εmμn+1),r为足够大的正常数, 它将由后文决定,而

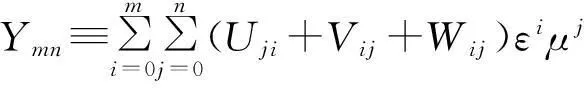
由假设,不难证明

α≤β, (t,x)∈[0,T]×(Ω+∂Ω)，

(32)

α≤g(t,x,ε,μ)≤β,

(t,x)∈[0,T0]×∂Ω,

(33)

α(0,x,ε，μ)≤h(x,Tα,ε,μ)≤β(0,x,ε,μ),

x∈Ω。

(34)

以下证明

(t,x)∈(0,T0]×Ω,

(36)

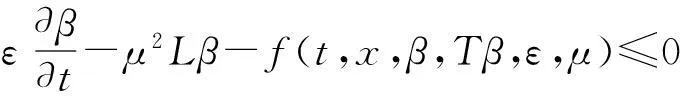
(t,x)∈(0,T0]×Ω。

(37)

由假设,存在正常数M,使得

fy(0,x,U00+V00,T(U00+V00),0,0)V00+fz(0,x,U00+V00,T(U00+V00),0,0)TV00+

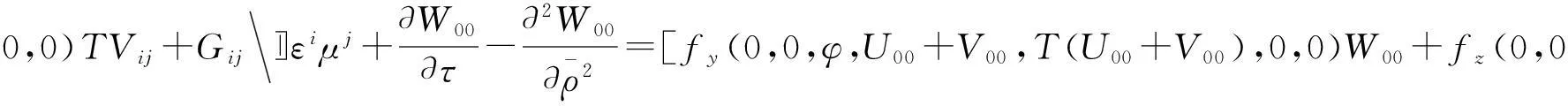
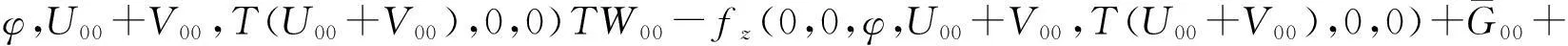
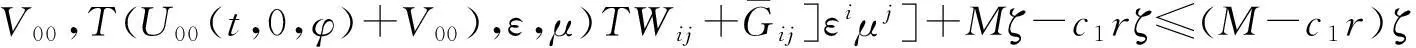
选择r≥M/c1,则不等式(37)成立。同理可证不等式(36)成立。

所以,由(32)-(36)式及比较定理[4]知,问题(1)-(3)存在解μ,并存在足够小的正常数ε1>0,成立关系式

a(t,x,ε,μ)≤u(t,x,ε,μ)≤β(t,x,ε,μ),

(t,x,ε)∈[0,T]×(Ω+∂Ω)×[0,ε1]。

再由(31)式,得到

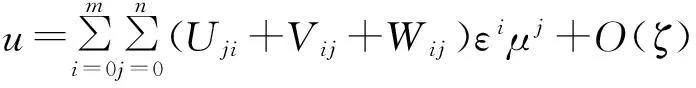
0<ε,μ≪1。

因此,在(t,x)∈[0,T]×(Ω+∂Ω)上,关于小参数ε、μ成立一致有效的渐近展开式(30)。定理证毕。

5结语

本文讨论的是非线性奇摄动问题,利用一个近似方法得到问题的近似解析解。它不同于一般的数值方法和单纯的模拟方法,用该方法得到的解的表示式能够继续进行解析运算。于是，由相应的近似解的表示式，我们还能够用微分、积分等解析方法来进一步研究方程解的定性和定量方面的性态。

参考文献:

[1] De Jager E M, Jiang Furu. The theory of singular perturbation[M].Amsterdam: North-Holland Publishing Co., 1996: 229-260.

[2] Barbu L, Morosanu G.Singularly perturbed boundary-value problems[M].Basel: Birkhauserm Verlag AG, 2007:181-210.

[3] Kellogg R B, Kopteva N.A singularly perturbed semilinear reaction-diffusion problem in a polygonal domain[J].Journal Differential Equations, 2010, 248 (1): 184-208.

[4] Tian Canrong, Zhu Peng. Existence and asymptotic behavior of solutions for quasilinear parabolic systems[J]. Acta Mathematicae Applicatae Sinica, 2012,121(1): 157-173.

[5] Skrynnikov Y. Solving initial value problem by matching asymptotic expansions[J].SIAM Joural Mathematics Analysis, 2012,72(1):405-416.

[6] Samusenko P F. Asymptotic integration of degenerate singularly perturbed systems of parabolic partial differential equations[J].Joural Mathematics Science,2013, 189(5):834-847.

[7] 贾云锋, 薛盼. Banach空间上一类微分系统解的存在性与唯一性[J].陕西师范大学学报： 自然科学版, 2013, 41(2): 5-8.

[8] 张英, 李晓燕, 姚若侠. 用改进的双曲正切法求解KP方程新的精确解[J].陕西师范大学学报：自然科学版, 2013, 41(5): 1-4.

[9] 臧辉, 聂华.一类具有强Allee效应的捕食-被捕食模型正平衡态解的存在性[J].陕西师范大学学报：自然科学版, 2013, 41(5): 5-10.

[10] 韩祥临.一类非线性方程的激波解[J].数学物理学报, 2003, 23A(2): 253-256.

[11] 韩祥临.一类非线性方程奇摄动问题的激波解[J].应用数学学报, 2003, 26(2): 359-366.

[12] 韩祥临, 赵振江, 程荣军, 等.飞秒脉冲激光对纳米金属薄膜传导模型的解[J].物理学报, 2013, 62(11): 110202.

[13] Mo Jiaqi, Chen Xianfeng.Homotopic mapping method of solitary wave solutions for generalized complex Burgers equation[J].Chinese Physics:B, 2010,10(10): 100203.

[14] Mo Jiaqi, Han Xianglin, Chen Songlin.The singularly perturbed nonlocal reaction diffusion system[J].Acta Mathematicae Applicatae Sinica, 2002, 22B(4): 549-556.

[15] Mo Jiaqi, Lin Wantao, Wang Hui. Variational iteration solution of a sea-air oscillator model for the ENSO[J].Progress in Natural Sciences, 2007, 17(2): 230-232.

[16] Mo Jiaqi, Lin Wantao.A class of nonlinear singularly perturbed problems for reaction diffusion equations with boundary perturbation[J]. Acta Mathematicae Applicatae Sinica, 2006, 22(1): 27-32.

[17] Mo Jiaqi.A class of singularly perturbed differential-difference reaction diffusion equation[J]. Advances Mathematics, 2009, 38(2): 227-231.

[18] Mo Jiaqi.Homotopiv mapping solving method for gain fluency of a laser pulse amplifier[J].Science in China:G, 2009, 52(7): 1007-1070.

[19] Mo Jiaqi, Lin Wantao.Asymptotic solution of activator inhibitor systems for nonlinear reaction diffusion equations[J]. Journal of Systems Science and Complexity, 2008, 20(1): 119-128.

[20] Mo Jiaqi.Approximate solution of homotopic mapping to solitary wave for generalized nonlinear KdV system[J]. Chinese Physics Letters, 2009, 26(1): 010204.

[21] Mo Jiaqi.Singularly perturbed reaction diffusion problem for nonlinear boundary condition with two parameters[J]. Chinese Physics:B, 2010, 19(1): 010203.

[22] Mo Jiaqi，Lin Wantao.Generalized variation iteration solution of an atmosphere-ocean oscillator model for global climateplexity[J]. Journal of Systems Science and Complexity,2011, 24(2): 271-276.

[23] 莫嘉琪, 林万涛, 杜增吉.双参数非线性高阶椭圆型方程的奇摄动解[J]. 系统科学与数学,2013, 33(2): 217-221.

〔责任编辑宋轶文〕

GK201303008,GK201401004)

第一作者： 杨文彬, 男, 博士研究生, 研究方向为应用偏微分方程。E-mail:yangwenbin-007@163.com

*通信作者： 李艳玲, 女, 教授,博士。E-mail: yanlingl@snnu.edu.cn