带电粒子在正交的重力场和磁场中运动探悉＊

张争光

（咸阳师范学院 陕西 咸 阳 712000）

带电粒子在正交的重力场和均匀磁场中运动轨迹，一般来说比较复杂，通常要对粒子的动力学进行分析入手，运用牛顿第二定律列出微分方程来求解.该求解过程对数学要求比较高，而且往往把问题的物理原理湮灭在纷繁复杂的数学推导中，使得学生的物理思维和物理图像模糊不清，即使得到了正确的答案，也不能深入地理解其内涵和实质.出现知其然，而不知其所以然的尴尬情景.然而，在近年的高考中，该类问题却成为压轴题命题的一个热点类型，比如2013年福建高考的第22题，2008年江苏第14题等.因此本文就粒子竖直入射的情况下，在相互垂直的重力场和磁场中粒子的运动进行分析，探讨粒子的运动规律，揭示其所蕴藏的美妙的物理结论.

问题：如图1所示，空间存在一个范围足够大的垂直于xOy平面向里的匀强磁场，磁感应强度为B，让质量为m，带正电q的粒子从坐标原点O点沿y正向入射，初速度为v0，重力加速度为g，请对该粒子运动的规律予以讨论.

分析：带电粒子从原点竖直向下射入，除了有重力的作用之外，粒子在向下运动的过程中也会受到洛伦兹力的作用，因此合外力的方向不断变化，物体将做曲线运动，过程复杂而难以直接使用牛顿第二定律来分析.如果坚持使用牛顿定律来求解，就应该用到微分方程，这对于中学生的物理学习来说显然是不妥当的，因此本文采用中学生可以理解的运动合成与分解的方法来探讨.

图1

探讨1：带电粒子究竟应做什么运动？

首先我们将初速度水平方向的零分量分解成等大反向的矢量之和，即0＝v1＋（－v1），如图2所示.且使得v＝，因此可以矢量法则求得v的值，即12

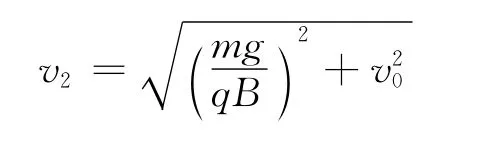
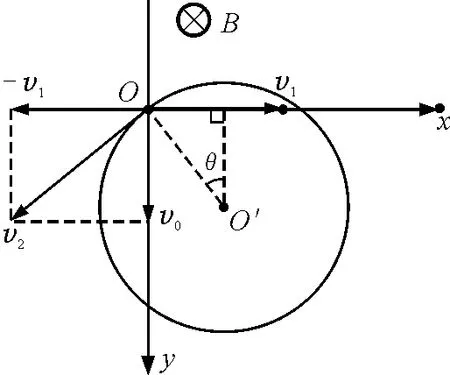
图2

这样一来初速v0就可以分解成v1和v2，因而粒子受到的洛伦兹力被分成两部分f1和f2.因此带电粒子在整个运动过程中，看成受到3个力的作用：1个重力，两个洛伦兹力f1和f2.分速度v1使粒子受到的洛伦兹力f1正好和重力等大反向，相互抵消，将以速度v1沿x轴做匀速直线运动；与此同时，分速度v2使粒子受到的洛伦兹力f2的作用，将以绕回转中心O′做匀速圆周运动.综上所述，带电粒子的运动可以看成两个分运动的叠加，一个分运动是以v＝沿轴做匀速直线运动；另一个分运动是在1xOy平面内做以速率大小为v2＝的匀速圆周运动.这两部分叠加的实际运动的轨迹是一条复杂的曲线，该粒子的分运动方程可以表示如下：

第一分运动的运动方程为

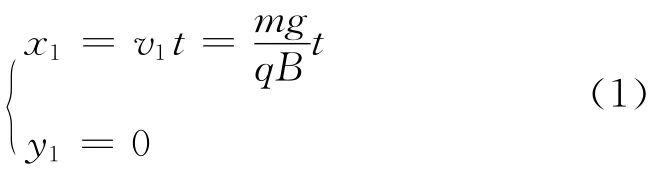
第二分运动是匀速圆周运动，此分运动的速率为

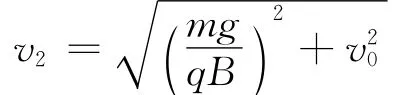
回转的半径为

回转中心O′坐标为

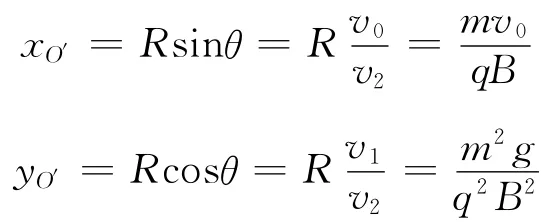
回转的角速度为

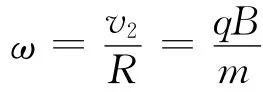
第二分运动的运动方程为

由于两个分运动合成，故将式（1）和（2）相加可以得到粒子在正交重力场和磁场中的运动轨迹方程

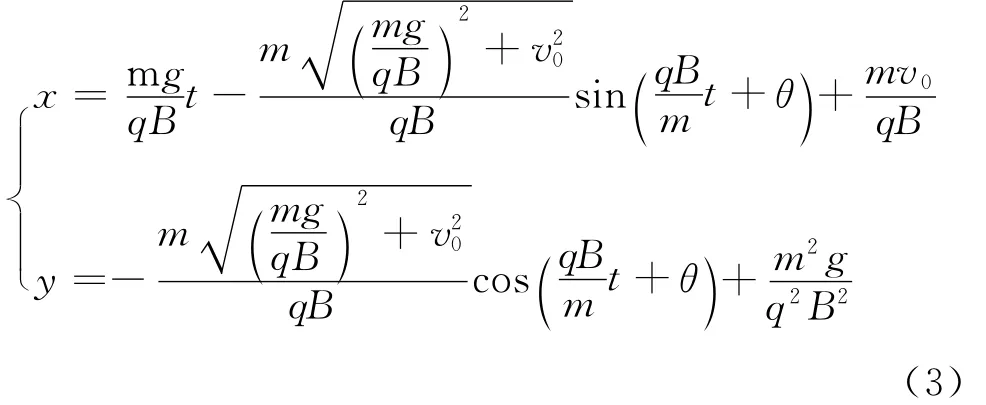
其中

依据该运动参数方程用软件画图，得到图3中的虚线就是粒子运动的轨迹，可见该轨迹是一条沿x轴方向延伸的长辐摆线.该图像也进一步说明带电粒子一方面在xOy平面内绕回转中心做匀速圆周运动，同时又随着回转中心沿x方向做匀速直线运动.使用这种运动合成的方法，学生对物理图像就会比较清楚，理解比较深入.不会出现求解微分方程以后，只有从数学运算的结果中确认带电粒子的运动轨迹，却不能深入理解为什么粒子会这样运动的情况.

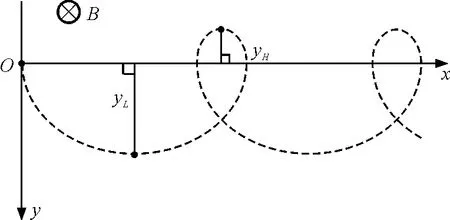
图3

探讨2：该运动蕴藏哪些美妙的规律？

（1）摆线的周期

由于粒子参与两个分运动，只有第2个分运动才具有周期性，即在xOy平面内绕回转中心做匀速圆周运动，因此摆线必定具有周期性，其运动的周期也就是匀速圆周运动的周期.

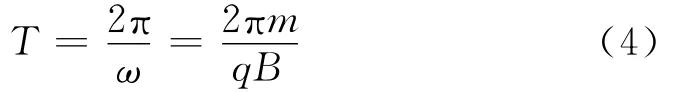
（2）粒子运动过程中下降的最大距离yL

所谓粒子下降的最大距离yL是指粒子经x轴下降的最大距离（如图3所示）.粒子下降过程最低点时的速度是最大速度，该速度的值一定等于v1和v2速度大小之和.由于该摆线运动具有周期性，只需要算出第一个周期内的下降的最大距离即可.粒子从原点O下落的的过程中只有重力做功，而洛伦兹力始终不做功，则根据动能定理有

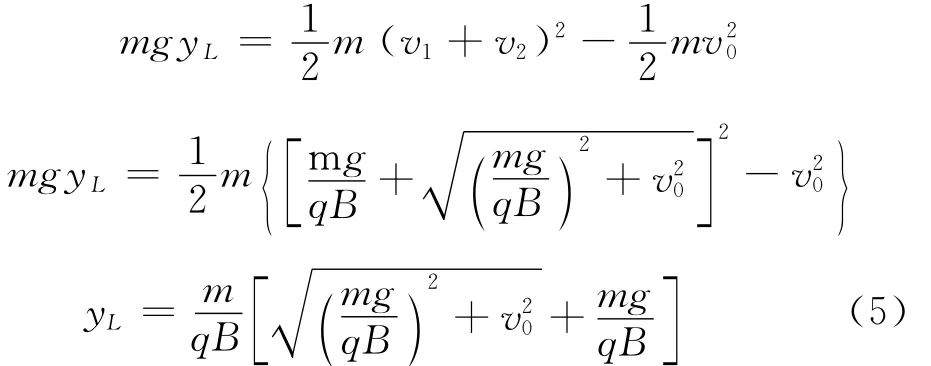
（3）摆线运动过程中上升的最大距离yH

粒子经过x坐标轴上升到最高点时的速度是最小的速度，该速度的值一定是v1和v2速度大小之差.

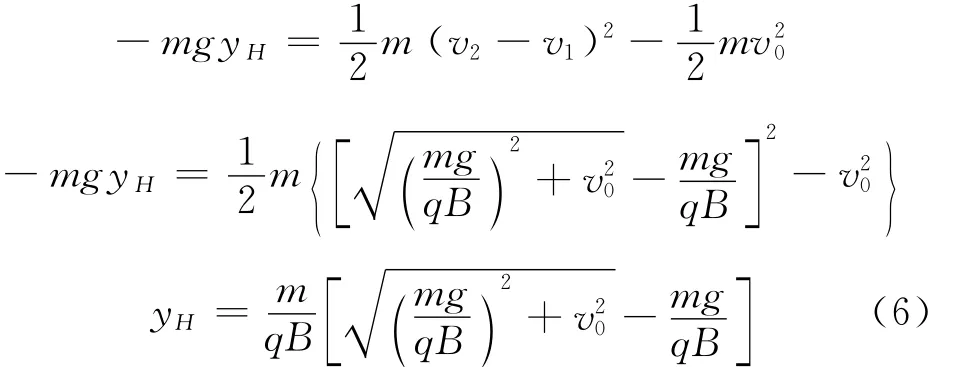
故有以下结论

其中R为粒子做匀速圆周运动的半径.由此可见，上升的最高点和下降的最低点的距离正好是第2个分运动的直径，这完全符合前面对该摆线运动合成规律的分析.

（4）vx与y 的比值

依据图2可得粒子在任意时刻的速度方程如下

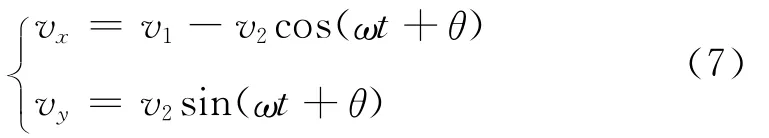
粒子速度的x分量与所在位置的y坐标之比

该结果可以发现一个美妙的结论，即任意时刻粒子速度的x分量与所在位置的y坐标成正比，该比例系数是一个常量，仅仅由粒子的质量、电荷量和磁场强弱来决定，与粒子的初速度等物理量无关.

（5）初速为零的运动特例分析

（1）运动的图像

将初速为零代入式（3）中，可以得到如运动轨迹方程如式（9）.

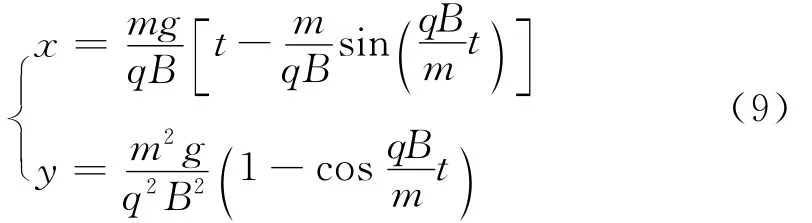
由上述该轨迹方程得到图4，从图中曲线来看，该粒子的运动轨迹就是一条普通的摆线.

图4

（2）粒子运动过程中下降的最大距离

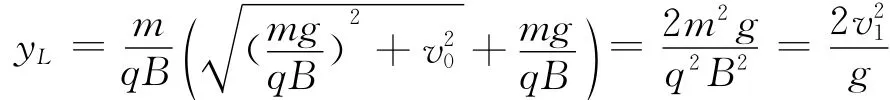
（3）粒子运动最低点的曲率半径

此类情况下v1＝v2，因此最低点的速度等于2v1，且最低点时重力和洛伦兹力的合力充当向心力，故有

R＝2yL这一有趣的结论表明，在场强为B的水平匀强磁场中，一质量为m，带正电q的粒子在O点由静止释放，粒子运动曲线在最低点的曲率半径正好为该点到x轴距离的2倍.

该摆线运动周期及其速度的水平分量和竖直速度的比值等规律因为前文已经进行描述，其大小与初速无关，因此无需做进一步的讨论分析.