任意梯形孔径的夫琅和费衍射＊

罗宏超

（沈阳航空航天大学理学院 辽宁 沈阳 110136）

成泰民

（沈阳化工大学 数理系 辽宁 沈阳 110142）

1 引言

衍射现象是光传播过程中的一种基本现象，是光的波动性重要体现，在实际中有很多重要应用：如孔径形状检测，微小物体形状识别等［1～4］.值得注意的是，在衍射过程中，孔的形状与衍射斑并不完全相像，随孔的形状不同衍射干斑形状会发生明显的变化，因此了解孔的形状与衍射干斑形状之间关系就显得十分重要.

从基尔霍夫衍射理论公式出发，推导了任意梯形孔的Fraunhofer衍射光强分布特征，进而找出了不同的梯形孔在屏幕上出现的Fraunhofer衍射图样的规律，并可以扩展到矩形、平行四边形等形状，具有一定代表性，对透彻理解Fraunhofer衍射规律具有重要意义.

2 不同梯形孔的Fraunhofer衍射强度

任意形状孔的Fraunhofer衍射可采用基尔霍夫衍射理论公式

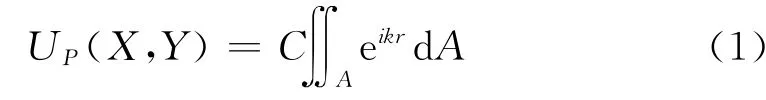
其中，UP（X，Y）是在屏幕上任意点P（X，Y）的电磁波函数的值，r是孔的某一微小面源至屏上的点P（X，Y）为止的距离，k是光的波矢值，C是与光源和观察点位置相关的一些物理量来确定的复常数.

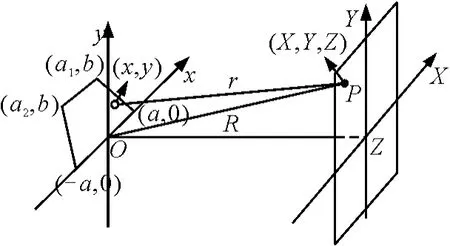
图1 梯形孔与屏上各点的坐标表示

根据图1的几何关系，经简化可得

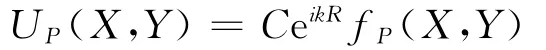
其中

对于任意的梯形孔而言

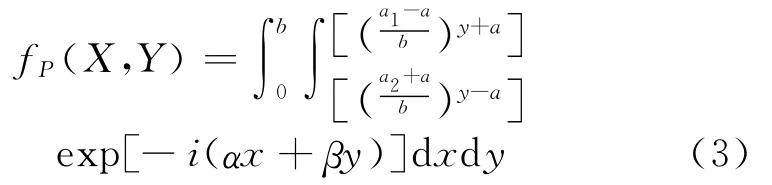
在屏幕上任意点（X，Y）的光的强度为

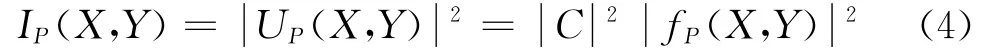
在屏幕中央点（0，0）上的光的强度为

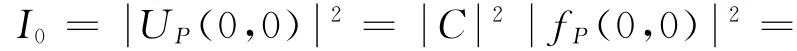
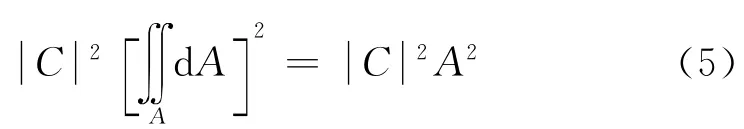
计算积分式（3），代入式（4）、（5）可以得到在屏幕上任意点（X，Y）的光的相对强度为

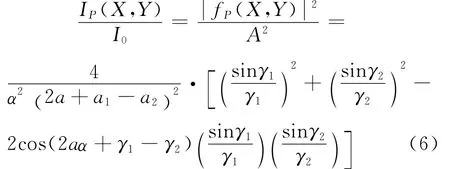
其中

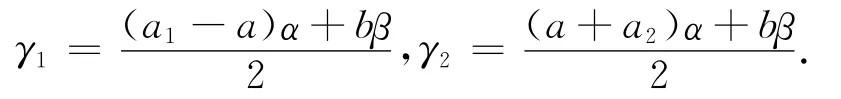
当a1－a2＝2a时，由式（6）可以回归到平行四边形孔情形，当a2＝－a；a1＝a时，由式（6）可以回归到矩形孔情形.因此，可以利用式（6）模拟任意形状的梯形孔在屏上的Fraunhofer衍射图样.

3 不同的梯形孔在屏上的Fraunhofer衍射图样的模拟

根据式（6），并利用 Mathematica软件中的DensityPlot函数［5～7］模拟了不同的梯形孔在屏上产生的Fraunhofer衍射图样，并以明暗表示二元函数值，如表1所示.

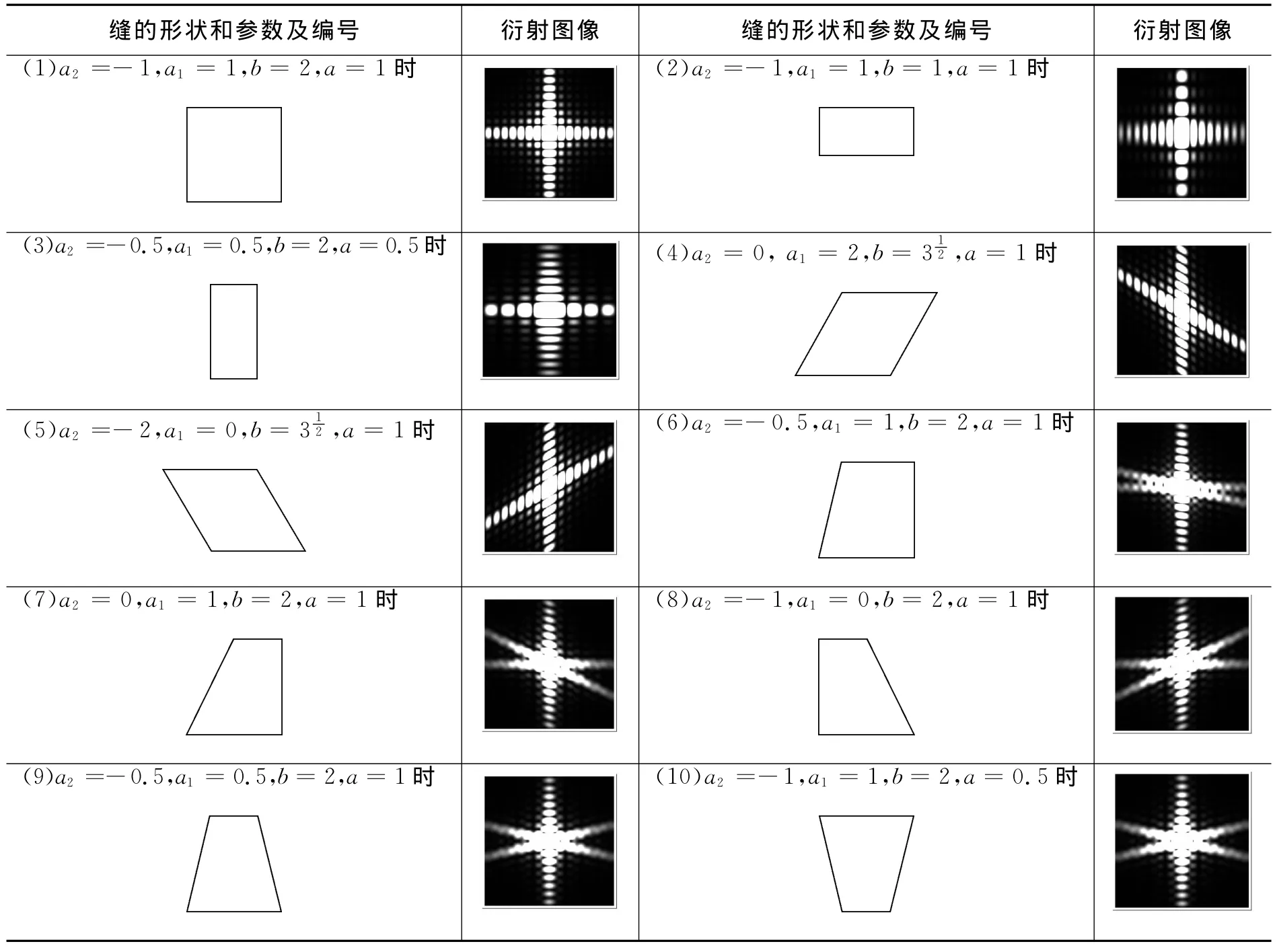
表1 不同梯形孔在屏上产生的Fraunhofer衍射图样

4 结论

根据表1的10张图可知，梯形孔的形状与Fraunhofer衍射图样之间的对应规律如下：

（1）不共线梯形的不同的边在单孔Fraunhofer衍射中，对屏幕处产生的衍射图样起很大的作用.明暗相间的衍射条纹与对应梯形的平行的两边垂直［如表1中图（1）～（5）］，对于不平行且不相邻的两边，将在两边各自垂直的方向上出现衍射亮纹［如表1中图（6）～（10）］.中央亮纹强度最大，强度随着级数的增加，迅速减弱.

（2）明暗相间的衍射条纹的宽度与两平行边之间的距离密切有关，两平行边之间的距离越小，对应的与平行边垂直方向的衍射条纹越宽，平行方向的越窄.

（3）只要梯形孔中有两条边平行，就会出现明暗相间的条纹.当两条边互不平行时，与梯形中不平行各边垂直的方向上出现连续的亮纹［如表1中图（7）～ （10）］.

1 姚启钧著.光学教程.北京：高等教育出版社，1989.94～151

2 马科斯.玻恩，埃米尔.沃尔夫著.光学原理 上册.北京：电子工业出版社，2005.342～428

3 羊国光，宋菲君编著.高等物理光学.合肥：中国科学技术大学出版，2008，87～103

4 Eugene Hecht，Optics，4thed.（Addison－Wesley，New York，2002），447～464

5 Stephen Wolfram.Mathematica.（Addison－Wesley，New York，1993），134

6 丁大正著.Mathematica4教程.北京：电子工业出版社，2002

7 成泰民，曹连刚.不同三角形孔的Fraunhofer衍射图样模拟.广西物理，2010，31（1）：33～36