超磁致伸缩泵悬臂梁阀流固耦合特性分析

朱玉川　陈　龙　杨旭磊

南京航空航天大学，南京，210016

超磁致伸缩泵悬臂梁阀流固耦合特性分析

朱玉川陈龙杨旭磊

南京航空航天大学，南京，210016

提出了一种采用悬臂梁式吸排油阀的超磁致伸缩液压泵结构，针对泵用悬臂梁阀工作时的流固耦合特性，基于单自由度振动理论与流固耦合作用下阀片振动参数等效计算原则，对超磁致伸缩泵悬臂梁被动阀进行了线性化数学建模，并在MATLAB/Simulink环境下进行了仿真研究。为研究其非线性特性，基于流固耦合力学原理，建立了超磁致伸缩泵悬臂梁被动阀流固耦合数值模型，并利用Comsol-CFD对其工作特性进行了数值求解。然后依据求解结果进行了深入分析，得到了阀片主要参数对泵性能的影响规律，为超磁致伸缩泵悬臂梁被动阀的主要结构参数的设计与优化提供相关依据。最后，通过不同厚度悬臂梁阀片在流固耦合作用下开启位移的线性理论结果与非线性数值结果的对比完成了模型验证，实验测试了超磁致伸缩泵的流量特性与阻断压力特性，得到了该泵峰值驱动频率为300 Hz左右。

超磁致伸缩材料；流固耦合；等效质量；开启压力

0　引言

随着现代飞行器的飞速发展，固定翼与旋转翼飞机越来越需要能够分布在机身的小型化高频宽作动系统，而基于智能材料的小型化高频宽电静液作动器为此提供了有效途径[1-2]。

超磁致伸缩材料(giant magnetostrictive material, GMM)具有磁致输出应变大、输出力大、响应速度快和能量传输密度高等特点，而超磁致伸缩执行器(giant magnetostrictive actuator, GMA)是基于GMM的新型电-机转换器，其应用研究已成为国内外研究的热点，目前以GMM与GMA为基础构建新型机载电静液作动器已经成为可能。因此，面向先进飞行器作动系统发展趋势以及航空领域对集成式机载液压作动系统的发展需求，开展新型集成式电静液作动器的研究具有显著现实意义，而驱动泵用单向阀性能是限制驱动泵与作动器性能提升的主要瓶颈与关键技术。

现有智能材料驱动泵大致可分为有阀泵与无阀泵两类。有阀泵是利用阀的开合性能来控制流体流动的；无阀泵是利用流体流过收缩入口和扩张出口，并通过出流和入流状态下的压力差来实现流体单向流动的，但在截止性能上无阀泵与有阀泵的差距较大。其中有阀泵的工作阀根据其工作原理又可以分成主动阀[3-4]与被动阀[5-7]。主动阀通常通过驱动电源的相位差来吻合驱动元件的工作状态，但是控制时序较为复杂，材料特性对阀的截止性能以及阀片滞性影响较大；相比之下，被动阀由于直接通过压差而实现阀的开合，具有结构简单、装配方便等特性，实际应用较广。

Gerver等[8]研制了一种利用磁致伸缩叠堆作为驱动元件的泵，用薄不锈钢圆片做成阀片，该泵的最大工作频率约为150 Hz。Mauck等[9]设计的一种基于压电叠堆的电静液作动器能够输出约4 W的功率，最大输出力能够达到271.7 N，但它的工作频率相对较低(在100 Hz以内)，需要通过被动阀进行频率校正。Sirohi等[10-11]设计了一种利用压电叠堆作为驱动元件的电静液混合作动器，输出功率能够达到2.5 W，最大输出力达到138 N，并且可以在一个相对较高的频率范围内工作(600～700 Hz)，该作动器通过两通滑阀来控制液压缸的双向运动。Lhermet等[3]研发了一种应用于多电飞机并配有主动阀的超磁致伸缩电静液作动器。

本文基于超磁致伸缩材料机理与容积式液压泵工作原理，设计了一种面向集成式电静液作动器的新型超磁致伸缩液压泵(giant magnetostrictive pump, GMP)，并在对现行的各种智能材料驱动泵所用单向阀详细分析的基础上，设计了一种新型一体式悬臂梁被动单向阀。通过对悬臂梁阀的线性化数学模型的理论分析与非线性流固耦合的数值分析，确立了该悬臂梁式被动单向阀优化设计准则与方法。

1　作动器与泵的结构及其工作原理

超磁致伸缩作动器由超磁致伸缩泵、液压缸、蓄能器、管道及配件组成，如图1所示。其中超磁致伸缩泵的具体结构如图2所示，驱动磁场闭合磁路由顶针、滑块、外罩、导磁块、GMM棒和底座构成。

图1　超磁致伸缩电静液作动器原理图

1.阀体　2.活塞　3.上端盖　4.输出杆　5.GMM棒　6.线圈骨架　7.外罩　8.底座　9.顶针　10.滑块　11.线圈　12.导磁块　13.碟簧　14.连接罩　15.泵头图2　超磁致伸缩泵结构

图2中，碟簧和顶针给GMM棒施加一定的预压力，通过调节顶针使预压力达到一个合适的值，可以增大GMM棒的输出位移和提高其磁机耦合系数。当给线圈通入驱动电流，在磁场作用下GMM棒产生一定伸缩位移，带动输出杆及与其连接的活塞做往复运动。当输出杆左移时，泵腔容积减小，在压力的作用下排油单向阀打开，油液通过管道流入液压缸下端，推动液压缸活塞向上运动。输出杆右移时，泵腔容积增大，吸油单向阀打开，油液进入泵腔，此时排油单向阀关闭。

2　悬臂梁阀流固耦合线性模型研究

以排油单向阀为例，排油单向阀在泵中的剖面模型如图3a所示，其等效模型如图3b所示。吸油阀和排油阀在实际工作中都可看作是单自由度的质量-弹簧-阻尼系统，由于流固耦合作用还需要注意以下两点：①阀片的开合由阀口的内外压差所决定；②由于阀片开合过程中阀片附近的油液对阀片运动特性的影响，数学模型应以等效阀片质量与等效阀片阻尼系数来表示。

(a)排油单向阀示意图(b)排油单向阀等效模型图3　悬臂梁式被动单向阀原理图

吸油阶段

(1)

排油阶段

(2)

其中，xRi与xRo分别为吸油阀阀片与排油阀阀片的开口位移量。

悬臂梁阀片工作时，考虑流固耦合作用下附着在阀片周围的液体的等效质量为[12]

(3)

式中，ρ为油液的密度；f为驱动频率；LR为阀片的长度；wR为阀片的宽度。

阀片的等效质量为[12]

(4)

式中,mR为阀片质量。

将式(3)代入式(4)可得

(5)

式中，ρR为阀片材料的密度；VR为阀片的体积。

(6)

式中，Δp为阀口内外压差；ρ为油液的密度；Cq为阀孔流量系数；A为阀孔截面积。

根据式(6)可以推导出排油与吸油时的流量(f≤300Hz)表达式[13]：

(7)

(8)

式中，w为阀口面积梯度。

GMP相关参数的取值如表1所示。

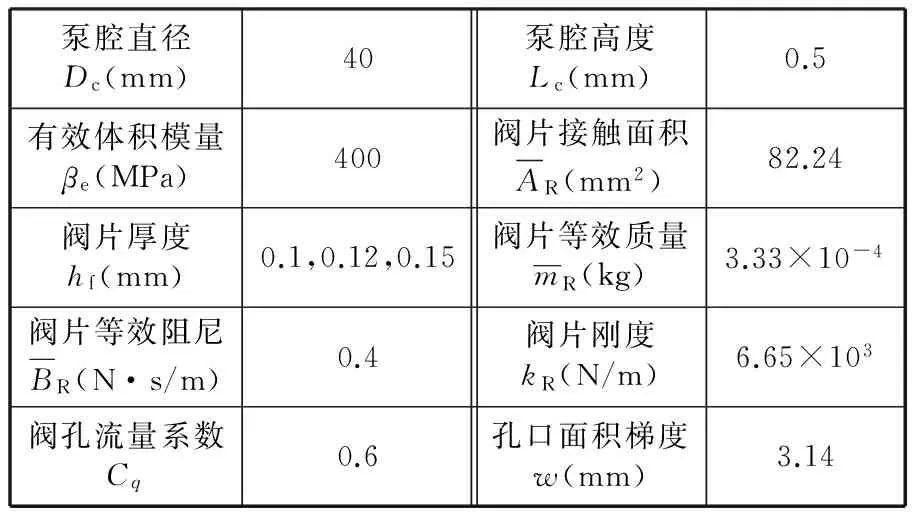
表1　GMP相关参数的具体值

在MATLAB/Simulink中编制仿真程序求解，当输入压差为16 kPa与32 kPa阶跃时，悬臂梁阀瞬态响应曲线分别如图4所示。

图4　阶跃输入下悬臂梁排油阀的响应曲线

当输入正弦压差的幅值分别为16 kPa与32 kPa，且频率为1 Hz时吸排油悬臂梁阀的响应曲线如图5所示。

图5　正弦输入下悬臂梁吸油阀与排油阀的响应曲线

3　悬臂梁阀流固耦合非线性数值研究

3.1流固耦合模型的建立

流体流入阀中将阀片打开而出流的过程是一个流体与阀片相互影响的复杂流固耦合过程。在模型中需严格输入阀口的内外压差以及阀片开启压力。有限元数值模拟中以排油阀为研究对象，排油阀的有限元模型如图6所示，阀片材料分别选择304不锈钢与铍青铜，相关参数如表2所示。

(a)有限元模型(b)网格模型图6　GMP排油阀的流固耦合模型

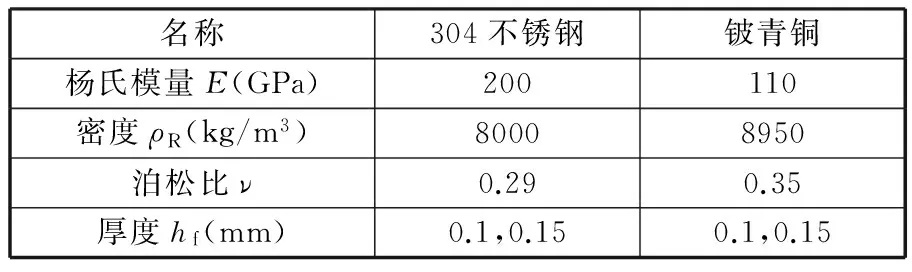
名称304不锈钢铍青铜杨氏模量E(GPa)200110密度ρR(kg/m3)80008950泊松比ν0.290.35厚度hf(mm)0.1,0.150.1,0.15

考虑在不同压差下阀的工作情况，仿真时将阀的入口处设定一合适的压力值，而出口压力设定恒为0。由于在达到最高流速时流体的雷诺数远小于500，故可设置流体为层流流动；同时为简化模型，假定流体为不可压缩流动。

3.2流固耦合分析结果

3.2.1不同阀片材料时的流场分析

图7是选定材料为304不锈钢和铍青铜阀片的流固耦合速度云图。由图7a与图7c对比可知在合适的相同压差作用下，铍青铜阀片所能达到的最大开口位移要比304不锈钢阀片所能达到的最大开口位移大，选用铍青铜阀片的排油阀中流速要比选用304不锈钢阀片的排油阀中流速大；由图7c以及表2的相关参数可知，由于铍青铜的刚度比304不锈钢的刚度要低，所以其弯曲变形较304不锈钢要大一些。

根据数值模拟结果，当阀片材料分别为304不锈钢与铍青铜时，阀口平均出流速度随压差的变化曲线如图8所示，其中阀片厚度为0.1 mm。

(a)Δp=16 kPa,304不锈钢　(b)Δp=32 kPa,304不锈钢

(c)Δp=16 kPa,铍青铜(d)Δp=32 kPa,铍青铜图7　不同压差下阀的流固耦合速度云图

图8　阀口平均流速与压差及阀片材料的关系曲线

从图8中可以看出，采用304不锈钢阀片时可承受最大压差为35 kPa，选用铍青铜阀片时可承受最大压差为26 kPa；在承受最大压差时，液压油在选用铍青铜材料阀片的排油阀中流过时流速要小于在选用304不锈钢材料阀片的排油阀中流过时流速。所以具体选用何种材料做阀片要具体考虑实际中的压差以及材料的刚度特性等。由图8还可知，在不大于16 kPa的压差下，选用铍青铜阀片的排油阀出口的平均流速明显大于选用304不锈钢阀片时的平均流速。而针对不同材料阀片都有一个不同的额定压差值使得在该压差时阀口平均出流速度达到最大，选用304不锈钢阀片的排油阀的额定压差值要明显大于选用铍青铜阀片时的额定压差值，且在阀两端压差达到额定压差之前阀口平均速度会随着压差上升而上升，但是当压差大于额定压差值后，阀口平均速度会随之下降。

3.2.2阀片不同厚度时的流场分析

图9是不同压差、不同阀片(不锈钢)厚度(0.12 mm，0.15 mm)下的被动阀流固耦合速度云图。

(a)Δp=32 kPa,hf=0.12 mm(b)Δp=56 kPa,hf=0.12 mm

(c)Δp=48 kPa,hf=0.15 mm(d)Δp=96 kPa,hf=0.15 mm图9　不同压差下阀的流固耦合速度云图

由图7(阀片厚度0.1 mm)以及图9(阀片厚度0.12 mm与0.15 mm)可知，在同等压差作用下，阀片越厚，阀片的最大开口位移以及液压油从阀中流过的速度就越小，但越厚的阀片可承受的最大压差就越大，且将阀片打开所需的压力也越大。

图10　阀口平均流速与压差及阀片厚度的关系曲线

图10所示为根据数值模拟结果得到的阀口平均流速与压差以及阀片厚度的关系曲线。可以看出，对于同一阀片，增加阀两端的压差，阀口的平均流速就增大；但是由于阀口空间的限制，当阀片完全打开时，继续增加阀两端的压差，阀的流量却会减小；故对于不同厚度的阀片都有一个额定的压差值，在这个压差值时阀片被看作完全打开，而此时流体黏性损失最小。

由图10可知，对于选用不同厚度阀片的阀，其阀口平均流速相同时，越厚的阀片完全打开时所需压差就越大，其阀口所能达到的平均流速也越大，即阀的流量也就越大。

由以上分析可知，阀的工作性能依赖于阀片的厚度与阀体的几何结构。尽管薄阀片完全打开时所需要压差相对较小，但是其所能达到的最大流量却比厚阀片受到更大的限制，因此在允许的压力损失范围内可以通过比较流量需求来选择阀片厚度。

4　模型验证与实验结果

4.1模型验证

将以上非线性数值模拟结果与线性理论模型结果进行对比，考虑不同厚度阀片在不同压差流固耦合作用下阀片开启位移，对比结果如图11～图13所示。

图11　厚度为0.1 mm阀片位移与压差关系曲线

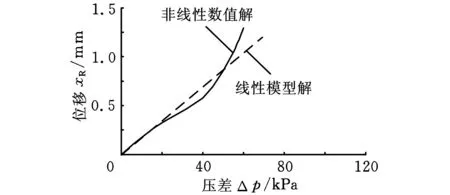
图12　厚度为0.12 mm阀片位移与压差关系曲线

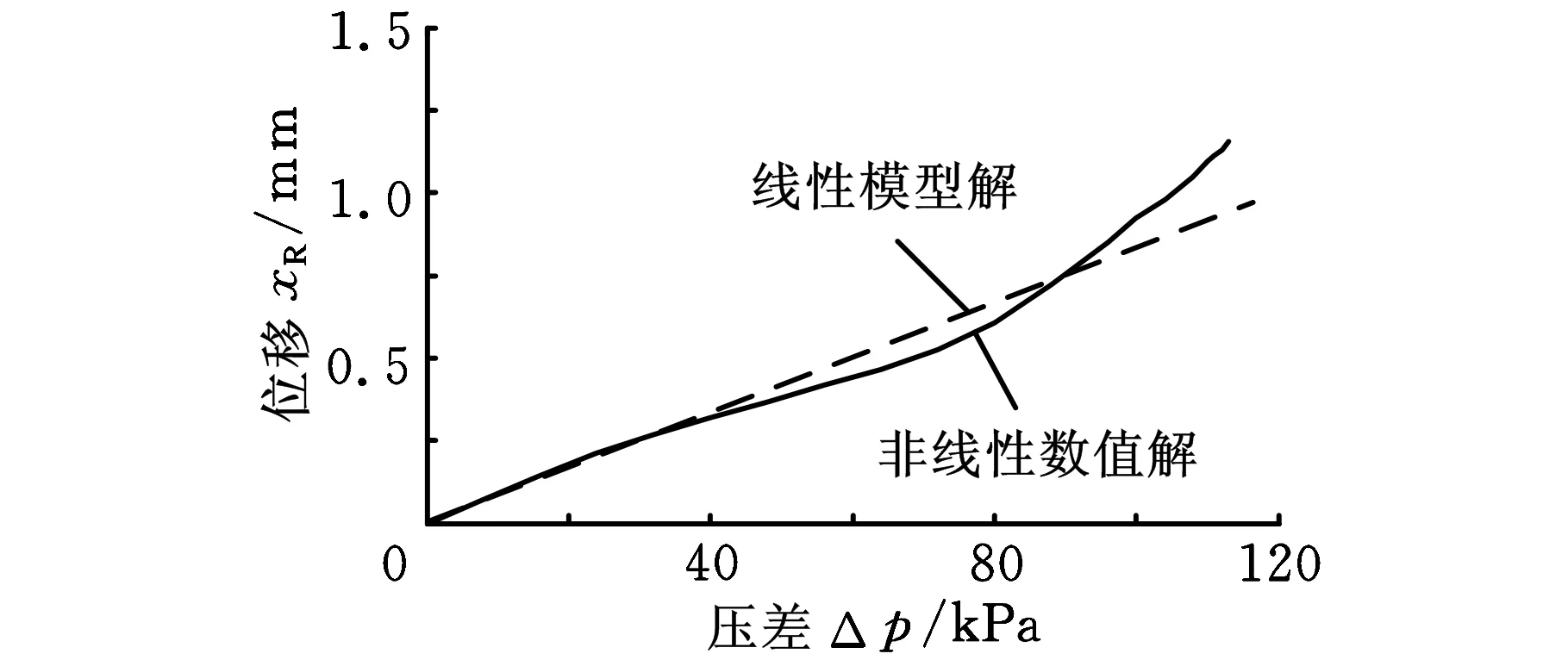
图13　厚度为0.15 mm阀片位移与压差关系曲线

图11～图13显示出最大开口位移与压差及阀片厚度的关系曲线(其中阀片材料为304不锈钢，由阀片安装空间决定的最大限制位移为2 mm)。

由图11～图13可知，线性模型结果显示阀片位移随压差而线性变化，而数值结果为非线性变化，但两者结果相差不大，反映出理论模型与数值结果可描述阀口附近液体流动与阀片开闭运动特性。

此外，同样可以看出，对于选用不同厚度的悬臂梁阀时，其阀口或阀片的开口位移相同时，厚阀片完全打开时所需的压差较大，且厚阀片所能承受的最大压差或压差范围更大。

4.2实验结果

在对GMA位移特性充分研究的基础上研究GMP的实际输出性能，测试时，给定输入幅值分别为2 V、3 V、4 V的正弦电压，实验样机与一体式悬臂梁单向阀如图14所示。

(a)超磁致伸缩泵(b)一体式悬臂梁单向阀图14　实验样机

实验中通过量筒或流量计读取流量数据，通过压力表读取阻断压力数据，并做好记录，最后将所测的实验数据经MATLAB处理成流量与输入电压和驱动频率的关系曲线，以及阻断压力与输入电压和驱动频率关系曲线。

GMP输出流量和阻断压力分别与输入电压、驱动频率的关系曲线如图15所示(图中点表示实测的数据，曲线是对数据点拟合后的四阶函数曲线，U为输入电压)。

(a)输出流量与驱动频率关系

(b)阻断压力与驱动频率关系图15　实验结果

从图15可以看出，在恒定输入电压下，GMP的输出流量开始随着驱动频率的增大而上升，但上升到一峰值后，却会随着频率的继续增大而下降；不同大小的输入电压对应的GMP峰值流量频率(简称峰值频率)也不同，而且随着输入电压越大，峰值频率就越大，但是随着输入电压不断增大其峰值频率增大幅度减小，GMP的峰值频率在300 Hz左右；驱动频率相同时，随着输入电压的增大GMP的输出流量也跟随增大，3 V输入电压相对于2 V输入电压流量增长比较明显，而4 V输入电压相对于3 V输入电压流量增大幅度相对减小很多。

5　结论

(1)设计了面向电静液作动器的超磁致伸缩驱动泵的结构，结合超磁致伸缩材料的工作机理，研制了超磁致伸缩泵用一体式悬臂梁被动阀。

(2)根据超磁致伸缩驱动泵的工作原理建立了驱动泵悬臂梁单向阀的线性化数学模型，通过MATLAB/Simulink对其运动特性进行了仿真研究，得到了超磁致伸缩泵用一体式悬臂梁被动阀恒定压力与正弦压力作用下运动特性。

(3)建立了超磁致伸缩泵悬臂梁被动阀非线性数值模型。利用Comsol-CFD对不同压差、不同厚度以及不同材料阀片等多种情况进行流固耦合数值研究，在此基础上进行了深入分析，得到了悬臂梁阀开启特性、阀片位移与阀口流速等特性规律，分析了阀片主要结构参数对其性能的影响机理，最后通过悬臂梁阀线性与非线性模型计算结果对比对数值求解进行了验证。

(4)实验测试超磁致伸缩泵流量特性与阻断压力特性，得到了GMP的峰值频率在300 Hz左右，且峰值频率随输入电压幅值变化；驱动频率相同时，随着输入电压的增大超磁致伸缩泵的输出流量也相应增大。

[1]焦裕松，焦宗夏，范开华.航空科学技术学科发展报告(2008-2009)[M].北京：中国科学技术出版社，2009.[2]Chaudhuri A, Yoo J H, Wereley N M. Design,Test and Model of a Hybrid Magnetostrictive Hydraulic Actuator[J]. Smart Materials and Structures, 2009,18(8):1-21.

[3]Lhermet N, Claeyssen F, Fabbro H. Electro-fluidic Components Based on Smart Materials for Aircraft Electrohydraulic Actuators[C]//The 9th International Conference on New Actuators. Bremen, Germany,2004: 14-16.

[4]Yoo J H, Sirohi J, Wereley N M. A Magnetor Heological Piezohydraulic Actuator[J]. Journal of Intelligent Material Systems and Structures, 2005, 16(11/12):945-953. [5]Chapman E G, Herdic S L, Keller C A, et al. Development of Miniaturezed Piezohydraulic Pumps[J]. Proceedings of the SPIE, 2005, 5762:299-310.[6]Kim G W, Wang K W. Switching Sliding Mode Force Tracking Control of Piezoelectric Hydraulic Pump Based Friction Element Actuation Systems for Automotive Trans-missions[J]. Smart Materials and Structures, 2009,18(8):1-15.

[7]Chaudhuri A. Self-contained Hybrid Electro-hydraulic Actuators Using Magnetostrictive and Electrostrictive Materials[D]. College Park,MD: University of Maryland, 2008.

[8]Gerver M J, Goldie J H, Swenbeck J R,et al. Magnetostrictive water pump[J].Proceedings of the SPIE, 1998,3329: 694-705.

[9]Mauck L D, Lynch C S. Piezoelectric Hydraulic Pump Development[J]. Journal of Intelligent Material Systems and Structures, 2000, 11(10):758-764.

[10]Sirohi J. Piezoelectric Hydraulic Hybrid Actuator for a Potential Smart Rotor Application[D]. College Park,MD: University of Maryland, 2002.

[11]Sirohi J, Chopra I. Design and Development of a High Pumping Frequencies Piezoelectric-hydraulic Hybrid Actuator[J]. Journal of Intelligent Material Systemand Structures, 2003, 14(3):135-147.

[12]Thomas E W. Development of a Smart Material Electrohydrostatic Actuator Considering Rectification Valve Dynamtics and in Situ Valve Characterization[D]. Athens,Ohio: Ohio State University, 2008.

[13]Kim G W. Design and Nonlinear Force Control of Power-by-wire Piezoelectric-hydraulic Actuator for Auto-motive Transmissions[D]. Pennsylvania: Pennsylvania State University, 2009.

(编辑郭伟)

Fluid-solid Coupling Analysis of Cantilever Valve in GMM-based Hydraulic Pump

Zhu YuchuanChen LongYang Xulei

Nanjing University of Aeronautics and Astronautics,Nanjing,210016

A novel structure of giant magnetostrictive pump (GMP) for the hybrid solid fluid actuator was designed. Aiming to fluid-solid coupling characteristics of cantilever valve in GMM-based pump, based on single degree of freedom vibration theory and equivalent calculation principle to parameters of cantilever valve, a linear model describing kinetic characteristic of cantilever valve was established and simulated. Further, aimimg to the nonlinear characteristic of fluid-solid coupling of cantilever valve, a numerical model with Comsol-CFD was built, accordingly numerical investigation for cantilever valve was performed, thus, the interaction relationship among main parameters of cantilever valve and performance of GMM-based pump was obtained, which provides a reference for parameter design and optimization of cantilever valve in GMM-based pump. Finally, the validity of above-mentioned numerical results was validated by comparing the simulation results with the theoretical one.

giant magnetostrictive material(GMM); fluid-solid coupling; equivalent mass; cracking pressure

2014-04-25

国家自然科学基金资助项目(51175243);江苏省自然科学基金资助项目(BK20131359)；航空科学基金资助项目(20130652011)；南京航空航天大学基本科研业务费资助项目(NS2013046)

TH137DOI：10.3969/j.issn.1004-132X.2015.03.003

朱玉川，男，1974年生。南京航空航天大学机电学院副教授。研究方向为智能材料电液控制技术。陈龙，男，1988年生。南京航空航天大学机电学院硕士研究生。杨旭磊，男，1989年生。南京航空航天大学机电学院硕士研究生。