基于运动相对性的六足机器人机体运动规划

李满宏　张明路　张建华　张小俊

河北工业大学，天津，300130

基于运动相对性的六足机器人机体运动规划

李满宏张明路张建华张小俊

河北工业大学，天津，300130

将处于支撑相的六足机器人视为时变的并联机构进行运动学分析，给出了姿态给定情况下机体工作空间的确定方法及边界方程。在此基础上基于运动相对性原理，提出将机体的运动规划转化为足端轨迹规划的方法，从而简化机体运动规划中逆解的求取问题，并通过仿真与实验进行了验证。结果表明：六足机器人在支撑相内机体的工作空间为至多是支撑腿条数个空心球体的交集，利用运动相对性原理对支撑相内机体的运动规划问题进行转化简便、可行。

六足机器人；工作空间；相对运动；运动规划

0　引言

六足机器人具有丰富的步态和冗余的肢体结构，能适应复杂的地理环境且具有较高的可靠性，在排险、军事、服务、农业等领域有着广阔的应用前景[1-2]。自20世纪80年代中期以来，国内外学者通过研究、模仿生物系统的结构、运动方式和控制方式，相继研制成功Genghis、Ariel、SPR-robot等多种性能卓越的六足机器人[3-5]。伴随着机器人的研制，六足机器人运动学在稳定性判据、步态规划和轨迹规划等方面也取得了丰硕的成果[6-8]。

六足机器人在运动过程中会存在摆动相和支撑相[9]。摆动相要解决的问题是运动过程中足端轨迹规划、避碰和时间节拍问题，而支撑相需要解决的问题则是各腿协调一致实现机体的移动[10]。目前，针对支撑相运动学研究相对较少，且主要集中在机体的工作空间和运动规划。六足机器人在运动过程中支撑腿条数及其落足点具有不确定性，故可将处于支撑相的六足机器人视为时变并联机构。虽然传统的并联机构理论对于常规并联机构工作空间和运动规划的求解相对简单，但其并不完全适用于此种特殊机构，对该机构进行运动学建模及求解难度相对较大。针对六足机器人机体的工作空间，文献中多采用蒙特卡罗等数值解法[11-13]，其理论价值与实用意义相对有限；而对于六足机器人机体的运动规划，多为解决机器人行进过程中的避障与路径优化问题[14-16]，很少考虑如何高效求取逆解以实现规划轨迹。

本文拟对六足机器人机体工作空间进行分析，在此基础上基于运动相对性原理将支撑相内机体的运动规划转化为机器人足端轨迹规划，以简化机体运动规划中逆解的求取问题，实现机体位姿的动态调整，并利用仿真与实验对分析结果进行综合验证。

1　工作空间

处于支撑相的六足机器人可视为一并联机构，其中，机体为动平台，由落足点构成的支撑多边形为定平台。当落足点固定时，考虑并联机构各支链与动、定平台连接点间的相对运动，可视支撑腿为类Stewart并联机器人[17]的支链，则六足机器人机体工作空间即为类Stewart并联机器人动平台的工作空间。

为便于分析，建立图1所示的运动学坐标系，其中C为躯干质心，Ai为第i条支撑腿的末端，即落足点，Bi为第i条支撑腿与机体的连接点。各坐标系坐标轴满足右手螺旋法则，ΣC为固定在机体质心上的机体坐标系Cxyz，z坐标轴垂直于机体平面背离重力方向，y坐标轴沿着机体轴线指向前进方向，ΣO为固定在地面上的参考坐标系Oxyz，L1、L2分别为股节和胫节的长度，θi为股节与胫节的夹角，实线和虚线分别表示处于支撑相与摆动相。

图1　六足机器人运动学坐标系

定义OPAi、OPBi、OPC分别为Ai、Bi与机体质心C在ΣO中的位置矢量，CPBi为Bi在ΣC中的位置矢量，Ri为Ai与Bi之间的距离。机体坐标系ΣC相对于参考坐标系ΣO的姿态矩阵ORC可用三个欧拉角α、β、γ表示为

q11=cosαcosβ

q12=cosαsinβsinγ-sinαcosγ

q13=cosαsinβcosγ+sinαsinγ

q21=sinαcosβ

q22=sinαsinβsinγ+cosαcosγ

q23=sinαsinβcosγ-cosαsinγ

q31=-sinβ

q32=cosβsinγ

q33=cosβcosγ

根据矢量在坐标系间的变换关系，可得

OPBi=OPc+ORCCPBi

(1)

由于OPAi为Ai在ΣO中的位置矢量，于是有

(2)

如OPc为(x,y,z)，通式NsM表示M点在坐标系ΣN下s轴上的分量，由式(1)、式(2)可得

(3)

xi=OxAi-q11CxBi-q12CyBi-q13CzBi

yi=OyAi-q21CxBi-q22CyBi-q23CzBi

zi=OzAi-q31CxBi-q32CyBi-q33CzBi

显而易见，式(3)为以Oi(xi,yi,zi)为球心，Ri为半径的球面方程。球心Oi的坐标由OPAi、CPBi和ORC决定。实际情况中，落足点的位置OPAi往往已知，CPBi由机器人的结构参数决定。因此，球面方程的球心通常仅与机体相对地面的姿态矩阵ORC有关。

在△AiBiCi中，根据余弦定理存在

(4)

于是有

(5)

综上可知，如果六足机器人的支撑腿存在n条，且给定了机体的姿态，那么六足机器人机体的工作空间是n个以Oi(xi,yi,zi)为球心、内径为Rimin、外径为Rimax的空心球体的交集。

2　机体运动规划

机器人在支撑相内机体的运动规划问题实质上为给定机器人机体位姿，快速求解相应关节转角，实现机体位姿动态调整的问题。对机器人进行运动学分析直接影响着机体平台的运动性能以及机器人整体的协调性、灵活性。

六足机器人在运动过程中支撑腿条数及其落足点具有不确定性，故可将处于支撑相的六足机器人视为时变并联机构。由于该机构支链条数与定平台参数在不断变化，当采用常规的并联机器人逆解求取方法求解该机构的逆解时，需根据支链条数与定平台参数实时调整高次三角方程组中方程的个数与参数，计算繁琐，因而常规的并联机器人逆解求取方法并不完全适用于此种机构逆解的求取。

运动的相对性是机械运动的一种性质，即同一个物体是运动还是静止，取决于所选的参照物。如人骑在马上向前奔跑的瞬间，在骑马人看来，马的身体没动，马蹄在动；而在路人看来，马蹄没动，马的身体在动。

得益于上述事实，发现机器人机体的运动轨迹与足端运动轨迹存在着密切联系。机器人机体在支撑相内移动过程中的每一时刻，落足点Ai与支撑腿和机体连接点Bi的相对位置是固定的。从固连在大地上的参考坐标系ΣO来看Ai是固定不动的，而从固连在机器人上的机体坐标系ΣC上看来Bi是固定不动的，于是可将参考坐标系中机体的运动轨迹转化为机体坐标系中足端Ai的运动轨迹。为简化六足机器人机体运动规划中逆解的求取，可将机器人规划的机体运动轨迹转化为足端轨迹进行逆解求取，不仅避免了常规方法中高次三角方程组的调整与求解，而且可根据支链条数灵活应用各支链的解析逆解快速求取整个并联机构的逆解。

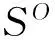
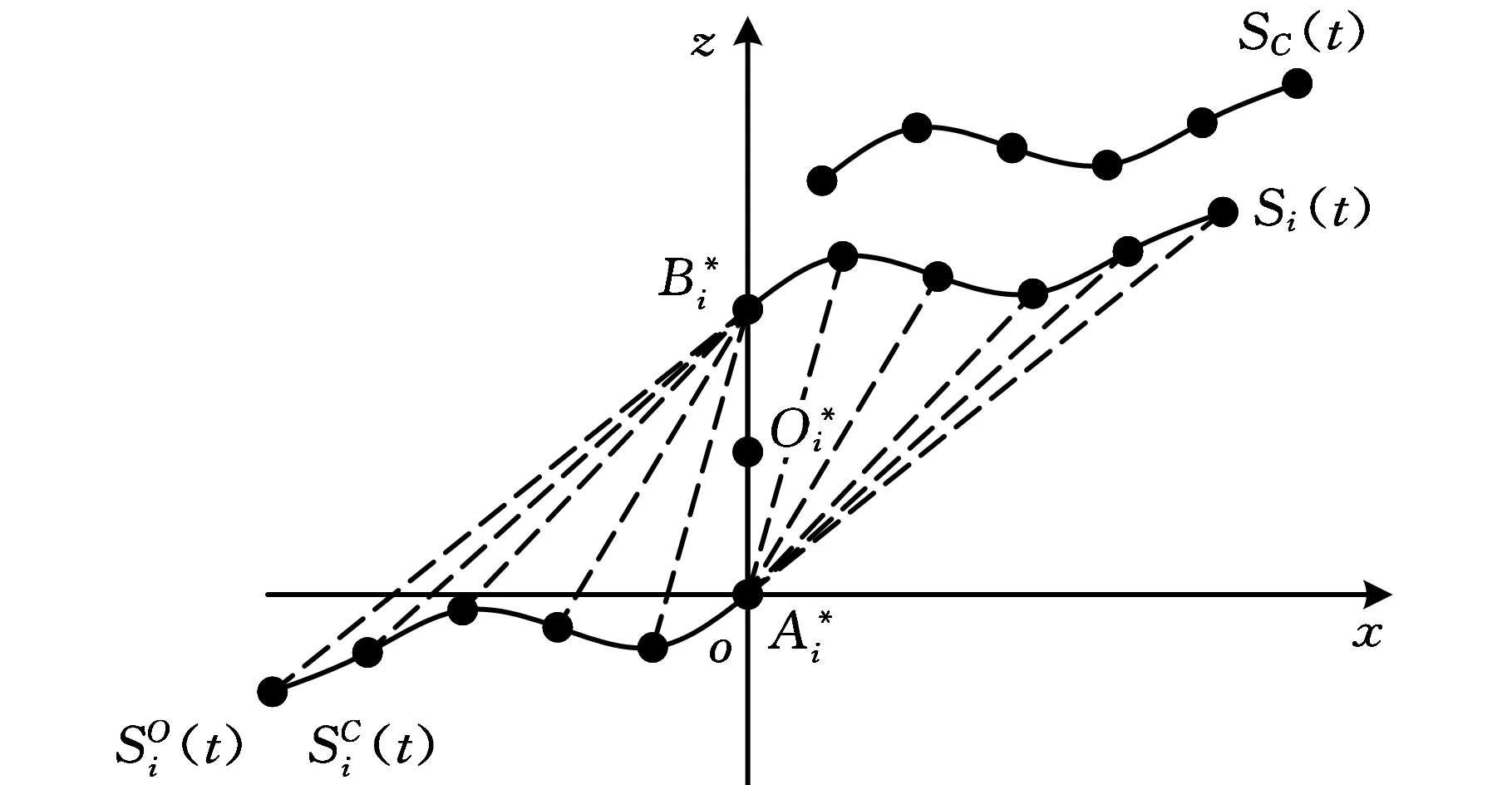
图2　运动轨迹间关系

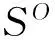
设机体质心在机体工作空间内的运动轨迹SC(t)为

(6)

曲线上任意一点为某一特定时刻质心在参考坐标系ΣO中的位置矢量OPC。

根据矢量在坐标系间的变换关系，可得

OPBi=OPC+ORCCPBi

(7)

于是有

(8)

则Si(t)的参数方程为

(9)

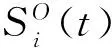
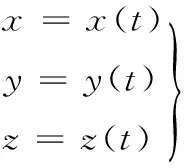
(10)

于是存在

(11)

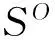
(12)

根据矢量在坐标系间的变换关系，可得

OPAi=OPc+ORCCPAi

(13)

(14)

(15)

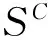
3　仿真与实验

针对六足机器人机体的工作空间和运动规划，利用设计的样机(图3)进行了相应的仿真与实验。样机的结构尺寸如图4所示。机体宽度W为50 cm，机体长度L为100 cm。机器人6条结构相同的腿对称布置于机体两侧，其中股节长度L1为30 cm，胫节长度L2为50 cm。假设机器人开始运动时机体水平，支撑腿的股节水平且其轴线与机体中轴线垂直，股节与胫节的夹角θi均为53°。为计算方便，将机体坐标系建于机体质心之上，参考坐标系建于质心正下方的大地上，则A1、A2、A3在ΣO中的坐标分别为(85,0,0)cm、(-85,-50,0)cm、(-85,50,0)cm，B1、B2、B3在ΣC中的坐标依次为(25,0,0)cm、(-25，-50,0)cm、(-25,50,0)cm。受机械结构限制，θi的取值为0°～90°。根据式(5)，可求得58 cm≤Ri≤80 cm。

图3　六足机器人样机

图4　六足机器人参数

当决定机器人机体相对于参考坐标系姿态的欧拉角α、β、γ均取10°时，机器人机体的工作空间如图5所示，为三个空心球体的交集。图中星形为空心球体球心，菱形为机体质心，实线为支撑腿，虚线为摆动腿，三个空心球体的球心依次为(60.75,-4.28,4.34)cm、(-67.82,3.03,4.21)cm、(-53.69,5.52,-12.89)cm。

图5　欧拉角均取10°时机体的工作空间

当α、β、γ均取0°时，机体平面与地面平行，且左侧两支撑腿具有相同的结构，则可认为在与机体坐标系y轴平行的方向上机器人形成了平行四边形机构，产生了虚约束。该虚约束对机器人机体的工作空间不会产生影响。因此，求得的空心球体的球心中会有两个重合，机体的工作空间为两个空心球体的交集，如图6所示，球心依次为(60,0,0)cm、(-60,0,0)cm。此例表明了上述机体工作空间确定方法的正确性。

图6　欧拉角均取0°时机体的工作空间

如机器人机体工作空间内的质心轨迹SC(t)为

(16)

t∈(0,4π)

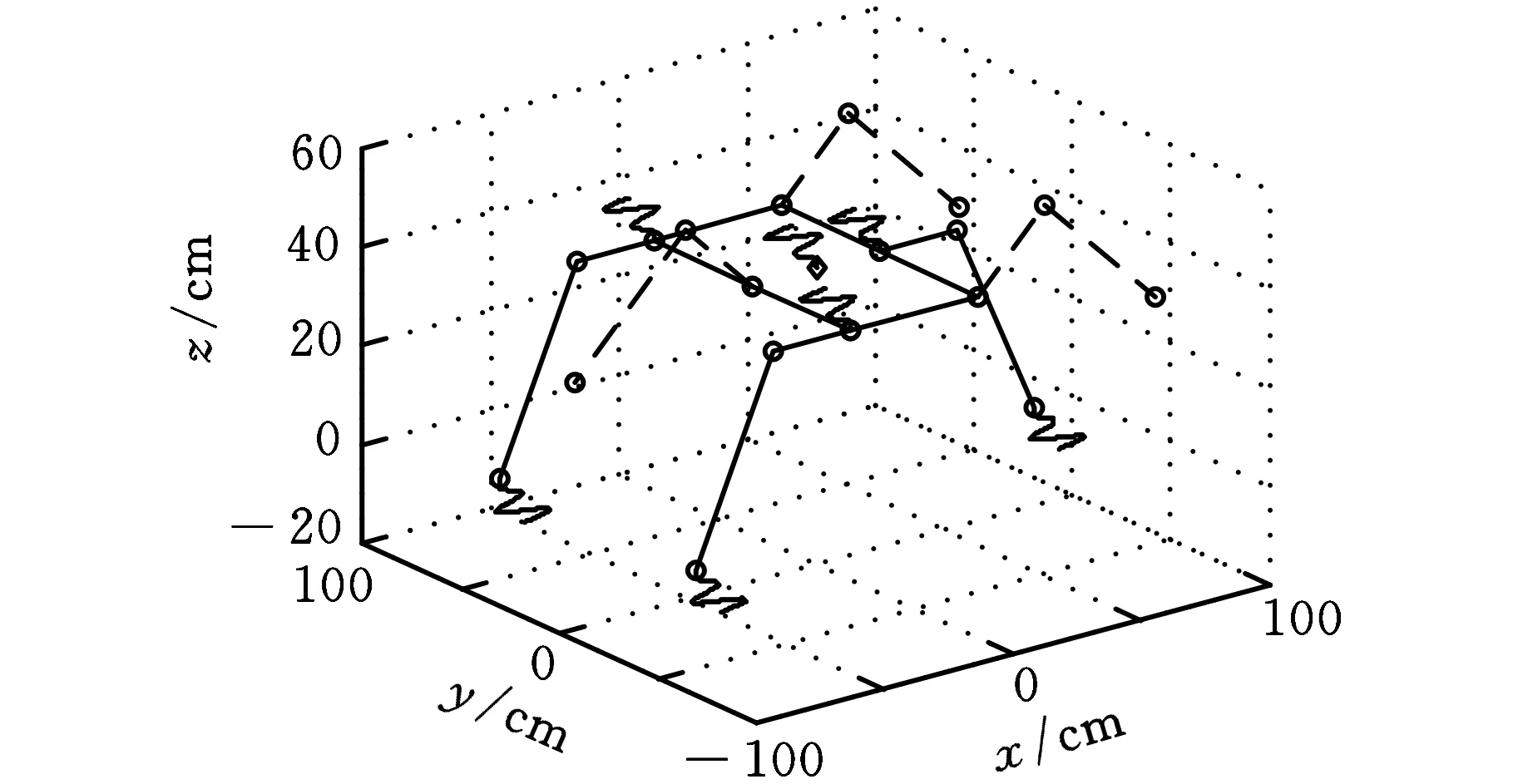
图7　六足机器人的运动轨迹

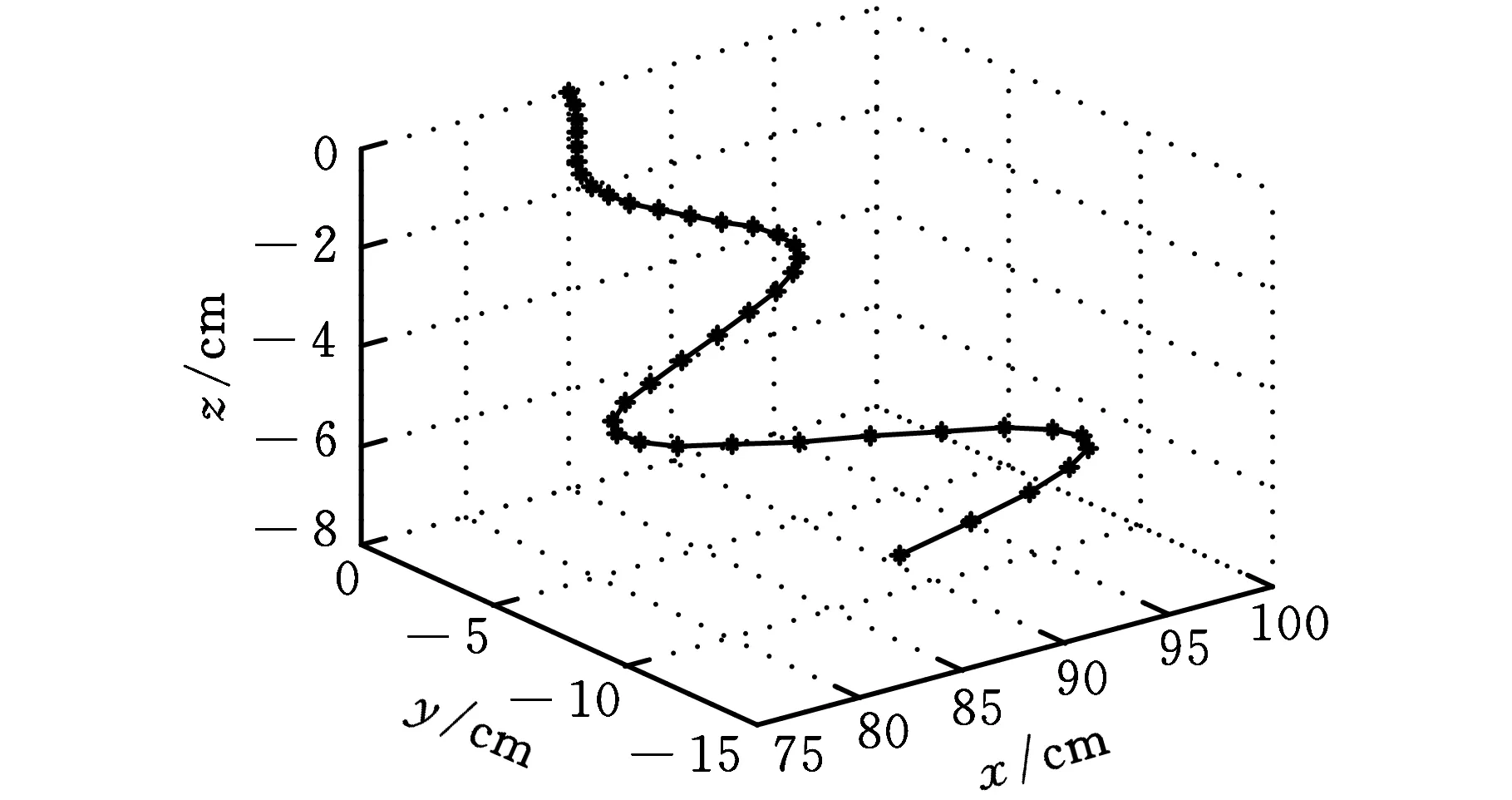
图8　六足机器人的足端轨迹

为进一步验证本文机体运动规划方法的有效性，采用该方法利用设计样机分别进行了调姿和步行实验。调姿实验中，机器人六足均处于支撑相且各落足点保持不变，机器人机体质心位置固定，仅将欧拉角中的β由0°调整为10°。图9a所示为机器人调姿实验的初始状态，其机体与各股节均处于水平状态。图9b所示为调姿实验的终止状态，β已调整为10°。在整个调姿过程中，机器人机体运动平稳，各关节动作协调。在机器人步行实验中，机器人以图9c所示的初始状态，向正前方前进50cm到达图9d所示的位置，整个运动过程连贯、平稳。机器人的调姿和步行实验表明，应用本文所提出的机体运动规划方法可实现时变并联机构机体位姿的动态调整，该方法准确、有效，能够满足六足机器人实时控制需求。

(a)调姿初始状态(b)调姿终止状态

(c)步行初始状态(d)步行终止状态图9　调姿和步行实验

4　结论

(1)对处于支撑相的六足机器人进行运动学分析时，可将其抽象为时变的并联机构，借鉴并联机器人的相关理论以简化分析。

(2)六足机器人机体的工作空间与支撑腿的条数、落足点的位置、机器人自身的结构参数和机体的姿态有关。机器人机体姿态给定时，其工作空间为至多为支撑腿条数个空心球体的交集。

(3)基于运动的相对性原理，可将机器人机体的运动规划问题转化为各支撑腿的足端轨迹规划问题，以简化机体运动规划中逆解的求取。机器人机体的运动轨迹在其工作空间内连续时，转化的各支撑腿的足端轨迹连续。

(4)仿真与实验结果表明，本文所阐述的方法准确、可行，且便于控制算法的编写。

[1]魏武, 李金龙, 任回兴. 基于吸盘负压吸附的六足爬墙机器人关节转矩优化分配[J]. 中国机械工程，2013, 24(10): 1289-1295.

WeiWu,LiJinlong,RenHuixing.JointTorqueDistributionofaSix-leggedWall-climbingRobotwithNegativePressureAdsorptionSucker[J].ChinaMechanicalEngineering, 2013, 24(10): 1289-1295.

[2]陈甫. 六足仿生机器人的研制及其运动规划研究[D]. 哈尔滨: 哈尔滨工业大学, 2009.

[3]黄麟, 韩宝玲, 罗庆生, 等. 仿生六足机器人步态规划策略实验研究[J]. 华中科技大学学报(自然科学版), 2007, 35(12): 72-75.

HuangLin,HanBaoling,LuoQingsheng,etal.ExperimentalStudyonHexapodBiomimeticRobot’sGaitPlanning[J].J.HuazhongUniv.ofSci. &Tech. (NatureScienceEdition), 2007, 35(12): 72-75.

[4]BrooksRA.ARobotThatWalks:EmergentBehaviorsFromaCarefullyEvolvedNetwork[J].NeuralComputation, 1989, 1: 253-262.

[5]KorayK,GeorgeG.ModelingandSimulationofanArtificialMuscleandItsApplicationtoBiomimeticRobotPostureControl[J].RoboticsandAutonomousSystems, 2002, 41(4): 225-243.

[6]ErdenMS,KemalL.FreeGaitGenerationwithReinforcementLearningforaSix-leggedRobot[J].RoboticsandAutonomousSystems, 2008, 56: 199-212.

[7]PortaJM,CelayaE.ReactiveFree-gaitGenerationtoFollowArbitraryTrajectorieswithaHexapodRobot[J].RoboticsandAutonomousSystems, 2004, 47: 187-201.

[8]王刚, 张立勋, 王立权. 八足仿蟹机器人步态规划方法[J]. 哈尔滨工程大学学报, 2011, 32(4): 486-491.

WangGang,ZhangLixun,WangLiquan.ResearchonaGaitPlanningMethodforaCrab-likeOctopodRobot[J].JournalofHarbinEngineeringUniversity, 2011, 32(4): 486-491.

[9]孟偲, 王田苗, 丑武胜, 等. 仿壁虎机器人的步态设计与路径规划[J]. 机械工程学报, 2010, 46(9): 32-37.

MengCai,WangTianmiao,ChouWusheng,etal.GaitDesignandPathPlanningforaGecko-likeRobot[J].JournalofMechanicalEngineering, 2010, 46(9): 32-37.

[10]阳如坤, 王泰耀. 全方位六足步行机器人运动规划的相对运动算法[J]. 机器人, 1992, 14(5): 44-47.

YangRukun,WangTaiyao.ARelativeMotionControlAlgorithmforOmnidirectionalSix-leggedRobot[J].Robot, 1992, 14(5): 44-47.

[11]宋孟军, 张明路. 仿生移动机器人并联机构运动学正解的鱼群算法求解[J]. 中国机械工程, 2012, 23(9): 1029-1036.

SongMengjun,ZhangMinglu.AnalysisofForwardKinematicsforBionicandMobileRobotwithAFSA[J].ChinaMechanicalEngineering, 2012, 23(9): 1029-1036.

[12]张建富, 王健健, 冯平法, 等.并联机器人可操作度分析的蒙特卡罗方法[J]. 农业机械学报, 2013, 44(7): 269-273.

ZhangJianfu,WangJianjian,FengPingfa,etal.MonteCarloMethodforManipulabilityAnalysisofParallelManipulators[J].TransactionsoftheChineseSocietyforAgriculturalMachinery, 2013, 44(7): 269-273.

[13]沈惠平, 马履中, 朱小蓉, 等. 全解耦并联机构的运动学与工作空间分析[J]. 农业机械学报, 2005, 36(11): 124-127.

ShenHuiping,MaLvzhong,ZhuXiaorong,etal.AnalysesofKinematicsandWorkspacefora3-DOFFullyDe-coupledParallelMechanism[J].TransactionsoftheChineseSocietyforAgriculturalMachinery, 2005, 36(11): 124-127.

[14]LocVG,RohSG,KooIM,etal.SensingandGaitPlanningofQuadrupedWalkingandClimbingRobotforTraversinginComplexEnvironment[J].RoboticsandAutonomousSystems, 2010, 58: 666-675.

[15]PratiharDK,DebK,GhoshA.OptimalPathandGaitGennerationsSimultaneouslyofaSix-leggedRobotUsingaGA-fuzzyApproach[J].RoboticsandAutonomousSystems, 2002, 41: 1-20.

[16]HaribKH,UllahAS,HammamiA.Ahexapod-basedMachineToolwithHybridStructure:KinematicAnalysisandTrajectoryPlanning[J].InternationalJournalofMachineToolsandManufacture, 2007, 47(9): 1426-1432.

[17]刘辛军, 张立杰, 高峰. 基于AutoCAD平台的六自由度并联机器人位置工作空间的解析求解方法[J]. 机器人, 2000, 22(6): 457-464.

LiuXinjun,ZhangLijie,GaoFeng.GeometricalDeterminationofWorkspacefor6-DOFParallelManipulatorsBasedonAutoCADPlatform[J].Robot, 2000, 22(6): 457-464.

(编辑郭伟)

Body Motion Planning for a Hexapod Robot Based on Relative Motion

Li ManhongZhang MingluZhang JianhuaZhang Xiaojun

Hebei University of Technology,Tianjin,300130

A hexapod robot in support phase was regarded as a time-varying parallel mechanism to make the kinematics analysis. The determination methods and boundary equations of the workspace were described herein for the hexapod robot whose body posture was given. Based on the relative motion theory, a method to transform body motion planning into foot trajectory planning was presented to simplify the issue of body motion planning. Simulation and experimental results show that the workspace for the hexapod robot in support phase is the intersection of the hollow spheres whose number is up to the number of the support legs and using the principles of relative motion to transform the issue of body motion planning in support phase it is simple and feasible.

hexapod robot; workspace; relative motion; motion planning

2013-10-27

国家高技术研究发展计划(863计划)资助项目(2012AA041508)；天津市自然科学基金资助项目(12JCYBJC12100)

TP242DOI：10.3969/j.issn.1004-132X.2015.03.006

李满宏，男，1987年生。河北工业大学机械工程学院博士研究生。主要研究方向为机器人运动学。张明路，男，1964年生。河北工业大学机械工程学院教授、博士研究生导师。张建华，男，1979年生。河北工业大学机械工程学院副教授。张小俊，男，1979年生。河北工业大学机械工程学院副教授。