匀加速运动声源的声场建模及其数值算法研究∗
吴波波 刘志红仪垂杰 马岩美
(青岛理工大学机械工程学院 青岛 266033)
匀加速运动声源的声场建模及其数值算法研究∗
吴波波刘志红†仪垂杰马岩美
(青岛理工大学机械工程学院青岛266033)
针对匀加速运动点声源的声场特性与其运动状态密切相关这一问题,提出匀加速直线运动状态下点声源的声场计算方法。利用此方法建立了匀加速直线运动时点声源的声压模型,对模型中的关键参数声矢量R进行数值解析,并对声压进行数值分析仿真,得出匀加速直线运动时固定接收点的声压数值计算方法。用此方法对固定接收点位置的匀加速点声源声压进行声场建模,结果表明:在声源接近接收者一定距离以后,声压明显增大;在此距离之外,距离对声压的影响不大。
匀加速运动,声场,声矢量
1 引言
随着汽车、飞机、火车等各种交通工具的普及和不断发展,城市的交通负担越来越重,其噪声污染日益成为环境污染的突出问题。交通工具的运动状态多变,多处于非匀速状态,
众所周知,汽车等运动声源在加速运动时噪声最明显,所以研究加速运动时噪声源的声辐射问题十分迫切。国内外学者对运动声源的声辐射研究也早已开始,并已经取得了一系列的成果,1968年P.M.Morse和K.U.Zngard[1]详细论述了运动媒质的发声机理、运动对声传播的影响,并讨论建立了匀速直线运动点源的声辐射数学模型;Tanaka K和Ishii S[2-3]推导了匀速直线运动线声源的声场理论解,指出它的声压幅值变化和频移特征与非运动点源的不同,但该研究不适用于有限长声源运动方向偏离物体轴线的情况,且忽略运动声源的表面声压和几何形状;P.L.Lee和J.H.Wang[4-5]在变速直线运动声源的声辐射方面进行了发展,建立了变速有限长直线运动声源声学位置矢量的数学表达式,他们指出描述声源与观察者关系的声学位置矢量是运动声场能否解析的关键,声学位置矢量的计算方法的不同是静止与运动声源声场计算的本质差别;王新龙[6]给出了匀速运动点声源的辐射声场和多普勒效应的推导结果,在此基础上周晓华[7]利用小波变换消除多普勒效应效果良好。但是,这些研究存在如下问题:一、运动声源的运动状态大多为匀速,对于匀加速运动声源的辐射声场研究较少;二、没有将加速时声学位置矢量的数值解应用到声场模型的建立中,对匀加速运动声源的声场没有解析。
本文针对以上两个问题提出了匀加速直线运动时声场的数值解析模型建立方法,并将匀加速运动时声学位置矢量的解析解应用的声场的建模中,通过对声压的数值仿真,得到了匀加速运动声源的声压空间分布,对现实具有很强的指导意义。
2 匀加速运动声源声场建模
设密度为ρ0的静止媒质中,存在一个匀加速声源,其沿z方向以加速度a,初速度v0运动,时间T=0时刻恰好通过坐标原点O,观察者位于S点,如图1。

图1 匀加速运动点源模型Fig.1 Model of point sound source with uniform acceleration
设观察点位置和时间坐标分别为[S(xs,ys,zs),t];源位置和时间坐标分别为[ξ(0,0,z(τ)),τ],则强度为Q(τ)的源的体积流和声压为[8]

式中R=|R(t)|表示声源到观察点之间的距离,R(t)定义为“声矢量”;g=t-τ-R/c0为延迟时间,q(S,t)为体积流函数。对于式(2),由解析格林函数法求解:

G(r,t/r0,τ)表示静止媒质对运动点源的响应。由Delta函数的性质可知式(2)的积分数值主要取决于Delta函数变量的零点[9-10]:
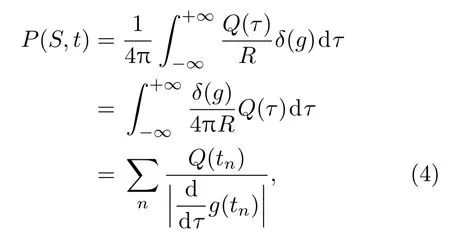
式中:tn为方程t-τ-R/c0=0的第n个根。由g=t-τ-R/c0等式两边对τ求导可得
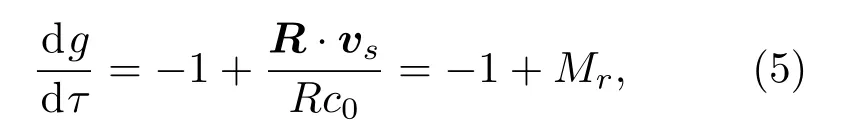
Mr为声源速度 vs在声矢量R方向上的投影与声速c0的比值。Mr>0时表示声源正在靠近观察者,Mr<0表示声源正在远离观察者。
对|Mr|<1时,方程g=t-τ-R/c0只有一个根,所以声压可以表示为

式(6)中
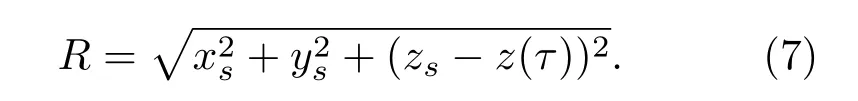
因为匀速直线运动和匀加速直线运动在此表达式中的区别仅在于声矢量R的表达式不同。所以,当a=0时,声源处于匀速运动状态,式(6)依然成立。
定义辅助函数
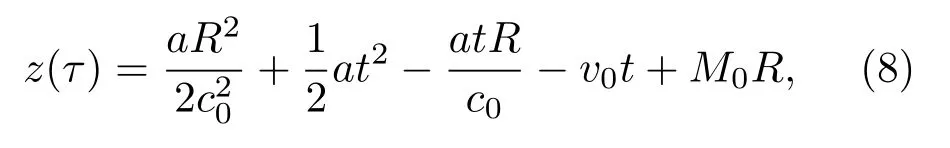
式中M0=v0/c0为初始时刻的马赫数。
式(8)的零点的物理意义是:t时刻接收到的声压信号时点源在τ时刻发出的,其中t和τ之间的关系,满足:

利用式(6)—式(8)即可数值求解匀加速运动点声源在某一固定接收位置的声场。
对比点声源声场公式从式(6)可以看出,声压幅值的增大和减小受到因子1/(1-Mr)的影响,当声源靠近观察者时Mr为正,影响因子变大,幅值变大;当声源远离观察者时,Mr为负、影响因子变小,幅值变小;这种由于运动引起的运动方向前部声压幅值变大,运动方向反向幅值变小的现象称为多普勒效应,而1/(1-Mr)即为多普勒因子。实际观察点的频率可表示为
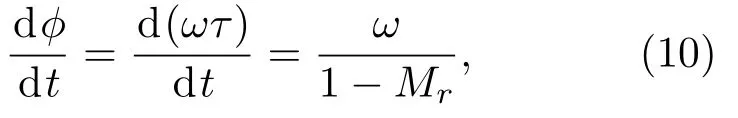
此即为多普勒效应的表达式。
3 关键参数声矢量R的求算
3.1声矢量R的计算方法
假设一个固定的观察者S在位置X0(T),运动声源S在接收时间T时刻的位置用矢量XS(T)表示,如图1所示。
位置矢量r(T)在此时可表示为
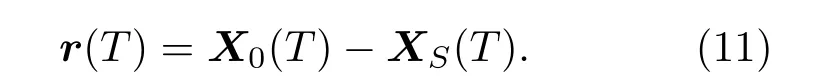
为了方便,r(T)称为动位矢。另外,声矢量R(T)的定义为
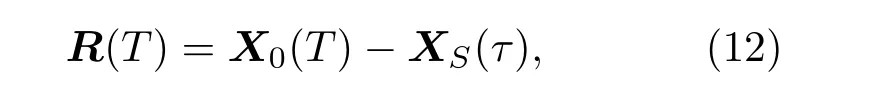
τ=T-(|R(T)|/c0)是声音的发出时刻,c0是声速。如果声源静止,那么式(11)和式(12)等价。声源以初速度V0,加速度a0沿直线运动。那么t时刻的声源位置为
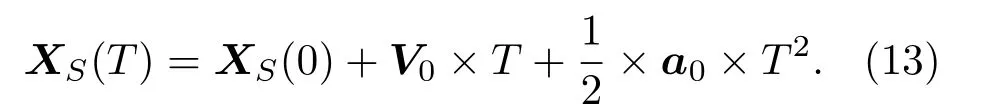
把式(13)带入式(12)并重新组合以后,在恒定加速度情况下的声矢量可以描述为
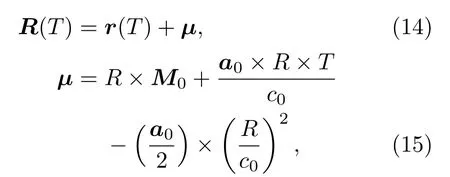
在式(15)中M0初始马赫数,R=|R(t)|,R与|R(t)|之间的关系如下:
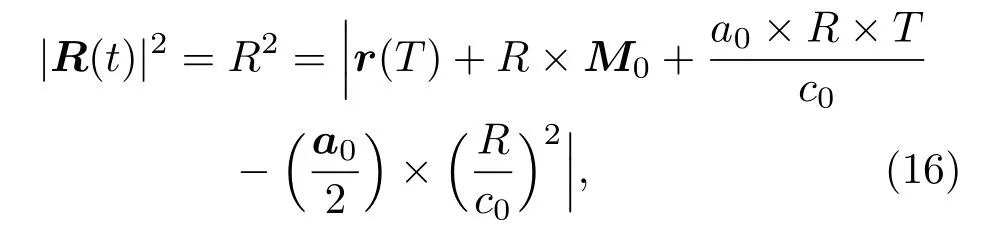
上式经变换后可简化为

其中A,B,C,D,E为系数,见附录A。其四个解可表示为以下形式:
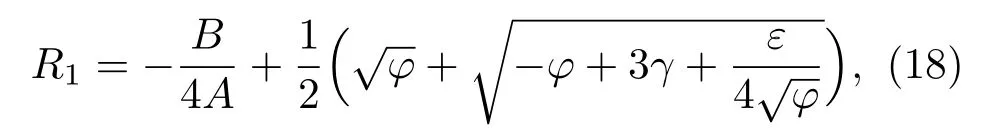
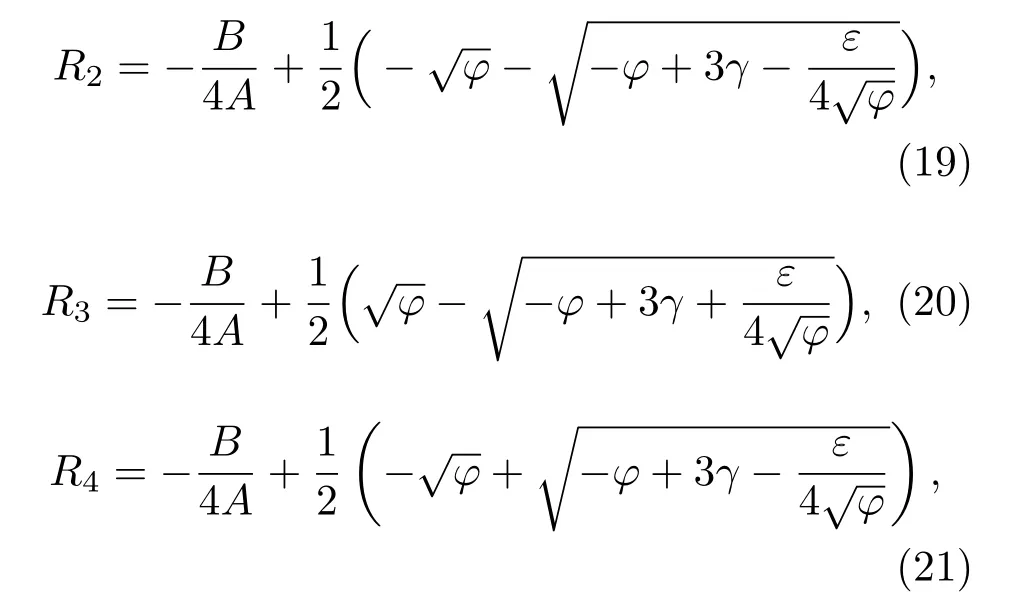
式中的系数ϕ,γ,ε见附录B。
3.2真实解筛选原则
公式式(18)—式(21)解出的声矢量R共有四个,R1~R4,但实际情况只有一种,所以只有一个解符合实际条件。由图1中可以看出,在声源沿z轴运动过程中,在到达运动路程中点之前,|R|>|r|,在过了中点以后|R|<|r|,根据这个原则可以筛选出需要的解。
3.3R的数值解析
假设加速度为:a0=(30,0,0)m/s2,R0=(0.2,0,0),声源初始位置XS(0)位于坐标原点,如图1。观察者位于O(L/2,D,0)处,L是运动路径的总长度,D=10 m,观察时间为1 s。将相关数据代入公式(18)—(21)可求得R1~R4和动位矢r1~r4式中(r=|r|),利用Matlab绘制出R1~R4,和r1~r4在不同时刻的相对位置如图2所示。
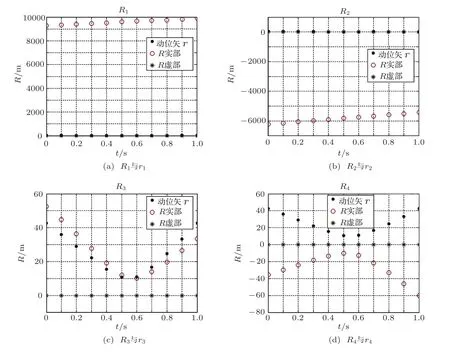
图2 同一时刻不同接收位置时R与对应的r的位置关系Fig.2 The positional relationship between R and r at the same time with different location
根据|R|>|r|的实际要求,从上面四幅图可以看出只有R3满足条件,这样就可以得到声矢量R的数值解析。
4 声场的数值模拟
4.1声场模拟
假设一个圆频率为250 Hz,源强Q=1的简谐点声源沿z轴匀加速运动,加速度为:a0=(30,0,0)m/s2,M0=(0.2,0,0),声源初始位置XS(0)位于坐标原点,如图1,D=10 m,观察时间为1 s,取四个观察点:S1(18,10),S2(38,10),S3(59,10)和S4(78,10)位置时符合要求的声矢量R如图3所示。
由图3很直观的可以看出,四个时刻均符合实际的解为R3。所以在此情况下的R可表示为
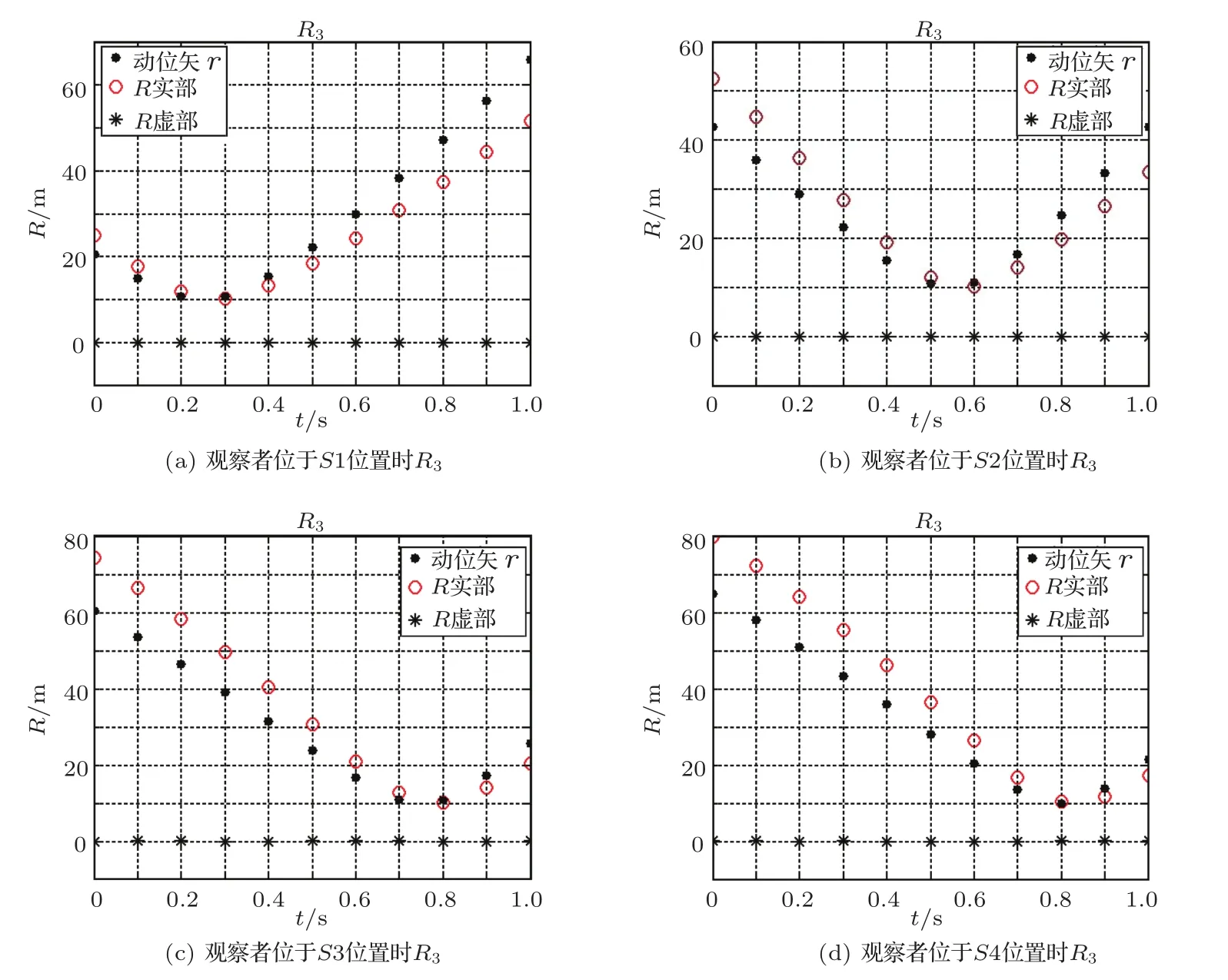
图3 各接受位置时符合条件的声矢量RFig.3 Acoustic vector R at each receiving position
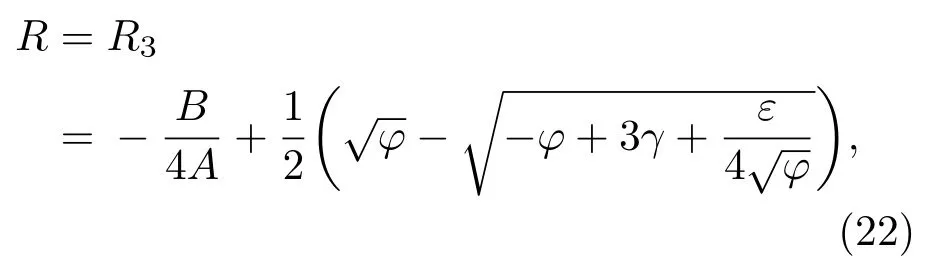
将系数带入即可,在得到R之后将R带入(6)式,即可得到声场的完整数值表达。此表达与Q(t)有关,由假设可知

带入声压公式(6)得到匀加速声源的声场数值表达,见图4。

图4 各接收位置时的声压图Fig.4 Sound pressure at each receiving position
图4为当M0=0.2、加速度a0=30 m/s2时,匀加速运动的简谐声源在1 s的观察时间内在各观察点的声场数值解析。
5 结论
本文根据运动声源声辐射基本理论讨论并建立了匀加速运动声源的声场模型。可以看出匀加速运动声源的声场与其声矢量R密切相关,理论上关于声矢量R的解难以求出,本文给出了匀加速运动时声矢量R的数值计算和筛选方法;通过分析可以得出,匀加速运动时声场的多普勒效应受到加速度的影响,在运动方向前后变得更加显著;同时,在加速度a=0的特殊情况下,文中所述的建模和解析方法同样适合于匀速运动,具有一定的一般性。
通过仿真得出了在点声源匀加速运动的时候某一固定接受位置的声场变化;从数值解析声场可以看出,在声源与观察者距离大于某一范围的时候,声压随距离的变化不明显;在点源距离观察者一定距离之后,越接近观察者,声压增加的越明显,在距离最近的时候声压达到最大,与实际情况相符。
[1]莫尔斯,英格特.理论声学[M].北京:科学出版社,1986:842-864.
[2]OBREZANOVA O A,RABINOVICH V S.Acoustic field generated by moving sources in stratified waveguides[J]. Wave Motion,1998,27(2):155-167.
[3]Yukio Iwaya,Yoîti Suzuki.Rendering moving sound with the Doppler effect in sound space[J].Applied Acoustics,2007,68(8):916-922.
[4]WANG J H,LEE P L.Determination of the acoustic position vector of a moving sound source with constant acceleration motion[J].Engineering Analysis with Boundary Elements,2009,33(8/9):1141-1144.
[5]LEE P L,WANG J H.The simulation of acoustic radiation from a moving line source with variable speed[J]. Applied Acoustics,2010,71(10):931-939.
[6]王新龙.运动点源的辐射[EB/OL].[2014-03-15]. http://xlwangnu.blog.163.com/blog/static/19071927020 1272361120331/,2012-08-23/2014-03-18.
[7]周晓华.运动噪声源识别技术的研究[D].吉林:吉林大学,2008:11-31.
[8]吴九汇,陈花玲,黄协清.旋转点声源空间声场的频域精确解[J].西安交通大学学报,2000,34(1):71-75. WU Jiuhui,CHEN Hualing,HUANG Xieqing.Acoustic solution of rotating point source in frequency domain[J]. Journal of Xi'an Jiaotong University,2000,34(1):71-75.
[9]刘志红.声辐射预估理论及其应用研究[D].青岛:青岛理工大学,2010:1-93.
[10]杜功焕,朱哲民.声学基础[M].南京:南京大学出版社,2012:202-243.
附录A
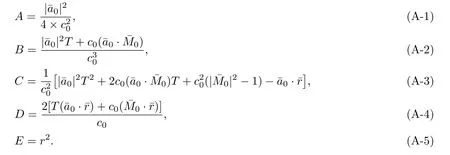
附录B
Acoustic modeling and numerical algorithms of uniformly accelerated motion of point sound source
WU BoboLIU ZhihongYI ChuijieMA Yanmei
(School of Mechanical Engineering,Qingdao Technological University,Qingdao 266033,China)
As the sound field characteristics of uniform acceleration motion are closely related to the moving states of the sound source,the article proposes a calculation method of sound pressure produced by uniform accelerated point source.Using this method to establish the sound pressure model of uniform accelerated sound source,it describes numerical analysis and simulation methods on acoustic vector and sound pressure.A numerical calculation method of sound pressure produced by uniform accelerated sound source can be obtained on condition that receiving position is fixed.The simulation results show that the sound pressure increases significantly when the sound source getting closely to the receiver in a certain distance,and beyond the distance,it has little effect on sound pressure.It can provide theoretical support for the similar study on moving sound source.
Uniform accelerated motion,Sound field,Acoustic vector
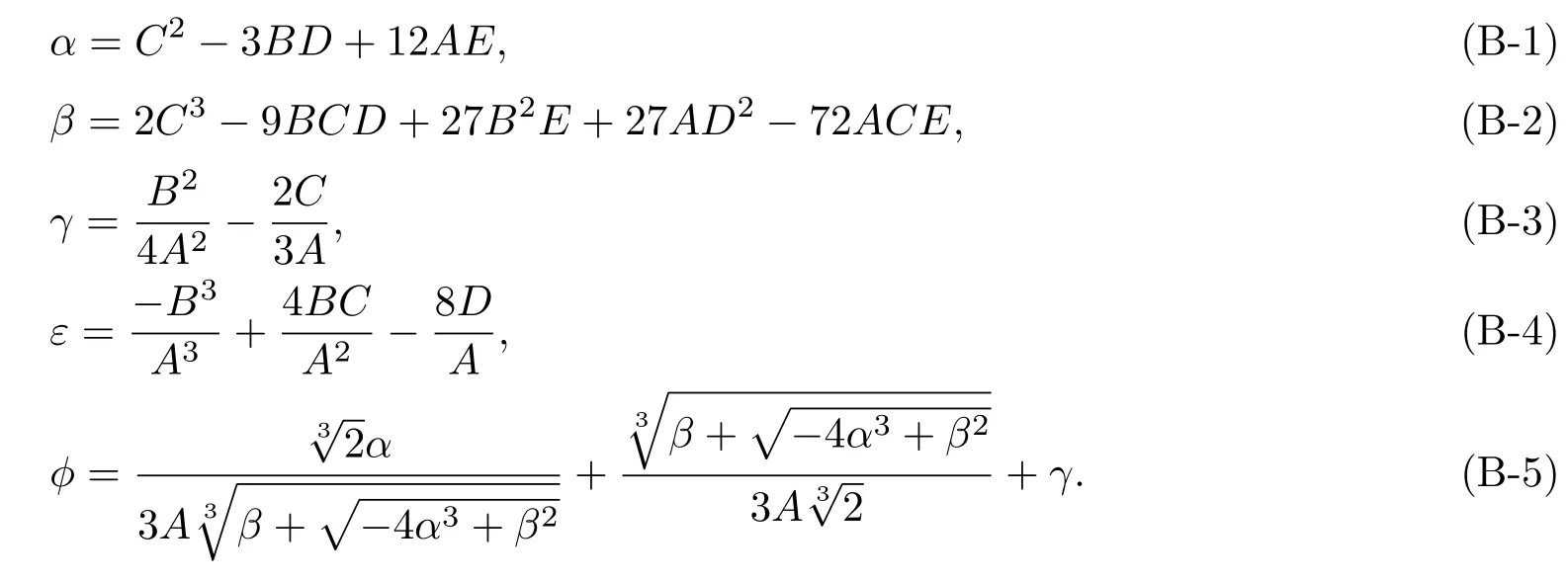
TN912.2
A
1000-310X(2015)02-0183-06
10.11684/j.issn.1000-310X.2015.02.015
2014-05-03收稿;2014-10-05定稿
∗国家自然科学基金项目(61271387)
吴波波(1990-),男,安徽宿州人,硕士研究生,研究方向:振动与噪声控制。
E-mail:Lzhqingdao@163.com

