一种消除测速模糊的梳状谱信号设计方法

陆扬　杨家庚　薛飞　张瑶

（1中国人民解放军91439部队　大连　116041）

（2中国科学院沈阳自动化研究所　沈阳　110016）

一种消除测速模糊的梳状谱信号设计方法

陆扬1†杨家庚1薛飞1张瑶2

（1中国人民解放军91439部队大连116041）

（2中国科学院沈阳自动化研究所沈阳110016）

相比于传统信号，梳状谱具有更好的混响抑制能力，但其容易产生多普勒测速模糊。为了解决这一问题，设计了一种新的几何梳状谱信号，通过分析测速模糊产生的原因，在传统频点计算方法的基础上，利用在信号频点计算中加入一组抗多普勒频率间隔的方法，以降低频点的重合。仿真分析证明，提出的梳状谱信号设计方法有效的减少了速度搜索时频谱重叠的程度，无论在噪声还是混响限制条件下均可以获得一个明显的输出峰值，避免了测速模糊的问题，可以获得比传统信号更好的检测性能。

梳状谱信号，多普勒速度模糊，信号设计

1　引言

发射信号波形设计是主动声纳系统设计的重要组成部分，其决定了系统的时频分辨能力、检测能力、抗混响性能等［1-2］。随着水声对抗向着浅海区域的发展，由于浅海近程受混响影响，这就要求声纳信号要具有良好的抗混响性能。常用的声纳信号如CW（Continuous wave）信号、LFM（Linear frequency modulated）信号虽然分别具有较好的频移与时延分辨能力，但其联合分辨能力均较差，对混响的抑制能力也有限［3］。

梳状谱信号具有类似钉板型的模糊度函数，具有良好的时延、频移联合分辨能力及抗混响能力，代表型的梳状谱信号由：几何梳状谱信号（Geometric comb waveform，GC）、正弦频率调制信号（Sinusoidal frequency modulated waveform，SFM）、调频脉冲串信号（Pulse train frequency modulation，PTFM）等［4-6］，这些信号各具特点，但也产生了一些新问题，如较高的峰均功率比（Peak average power ratio，PAPR）影响发射效率［7］；多普勒测速模糊的问题等［8-9］。本文针对梳状谱信号多普勒测速模糊的问题，对GC信号的频点设计展开研究，提出了一种新的GC信号频点计算方法，显著降低了由于多普勒测速模糊的现象，并通过仿真分析验证了算法的有效性。

2　典型梳状谱信号性能分析

一个信号的距离与速度分辨能力以及其抗混响能力，均可以通过对发射信号模糊度函数的分析来获得，模糊度函数定义如公式（1）所示［3］，其中τ是时延因子，f0为信号的中心频率，c为水中声速，v为目标速度，ξ=2f0v/c为频移因子。

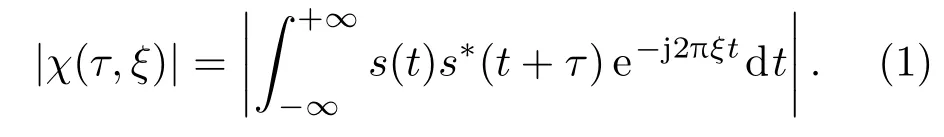
梳状谱信号是一类具有类钉板型模糊度函数的信号，相对于传统信号，其具有更好的抗低、高多普勒性能，典型的梳状谱信号有：SFM信号与GC信号。SFM信号的数学表达式为

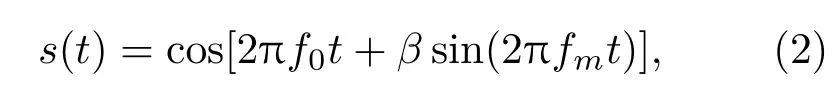
其中f0为信号的中心频率，β为调制指数，fm为调制频率，信号的带宽由β与fm决定，其表达式为

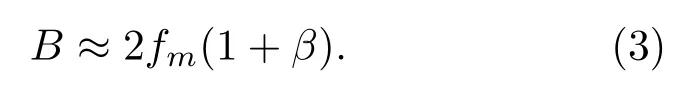
SFM信号的频谱表现为沿着中心频率f0对称分布的若干个线谱，相邻谱峰的频率间隔为fm，如图1（a）所示，从图中可以看出，SFM信号不同的谱峰其幅度是不相同的。计算其模糊度函数，得到模糊图1（b），从图中可以看出，其具有钉板型的模糊度图，由于其频域的能量分布不均，不同谱峰幅度差别较大，使得其距离模糊度函数为类三角形的包络，其测距性能稍差。

图1　SFM信号的频谱与模糊度图Fig.1 The spectrum and ambiguity graphs of SFM train

由于SFM信号频谱表现为一系列独立的线谱，当目标的径向速度较大时，会产生“多普勒测速模糊”，多普勒测速模糊的定义是当目标回波信号的多普勒频移较大时，会和发射信号的相邻谱峰重叠，从而导致测速模糊。

在不出现测速模糊的情况下，系统的最大可探测目标速度为

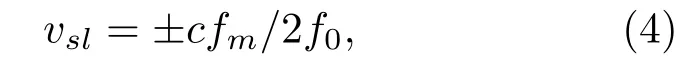
c为声速，通过设置fm，使得νsl大于系统探测的最大目标径向速度，从而避免多普勒的测速模糊。如果要所有频点均能满足以上要求，信号要占用较大的带宽，而对于水声信道而言，其可用带宽较窄，显然这种方法会造成频带资源的浪费。

GC信号的数学表达式为

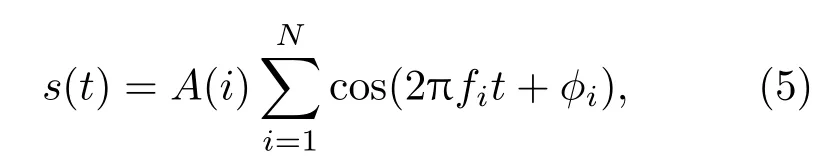
其中，A（i），fi，ϕi分别为信号的幅度、频率以及初始相位，信号的频率计算公式为

s为起始频率间隔，r是一个稍大于1的比例系数。从频率计算公式（6）可以看出，GC信号的频率间隔序列为一等比序列，由于信号的频率间隔不再是常数，在较低频点间隔较小，而在频率较高的频点其频率间隔也较大，相比于等间隔的SFM信号，GC信号有更好的频率利用率。

计算GC信号的频谱，如图2（a）所示，从图中可以看出，GC信号的频域能量分布较均匀，计算其模糊度函数，得到模糊度图2（b），从图中可以看出，GC信号的模糊度图也具有类钉板的形状，由于其频域能量更加平均，其主峰相对于SFM信号更加尖锐，其时延与速度模糊度图的旁瓣幅度大大降低，且距离主峰较远，其抗混响性能也优于SFM信号。不过，与SFM信号一样，GC信号也会存在多普勒速度模糊的问题，除此之外，由于GC信号是一种复合信号，它很容易因为各频点幅值的叠加而产生很大的瞬时功率，造成系统输出信号的PAPR较大，PAPR的定义为

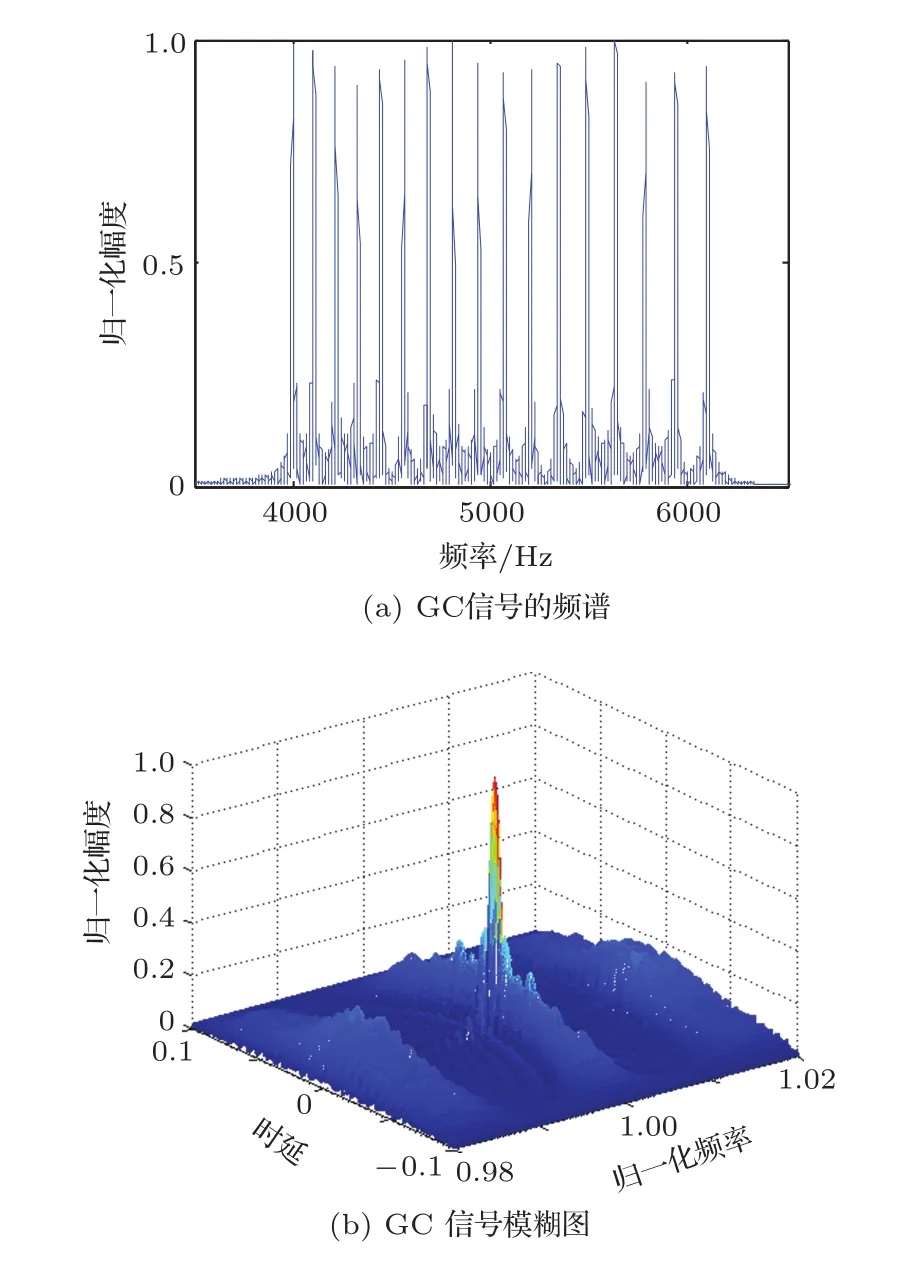
图2　GC信号的频谱与模糊度图Fig.2　The spectrum and ambiguity graphs of GC signal

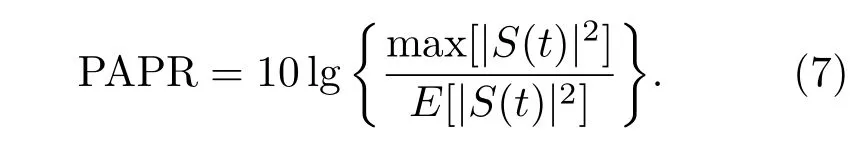
较高的PAPR不但会造成发射机功率的浪费，还会产生发射波形的失真。所以在利用这种信号之前都需要对其进行相位优化，以降低其PAPR，由于与本文讨论内容无关，这里不再累述。

3　改进的梳状谱信号设计

根据之前的分析可以看出，相比于SFM信号，GC信号具有更好的分辨能力及抗混响性能，其中的关键就是它的频域能量更加平均，并且在有限频段内能设置更多的频点，但前提是不产生测速模糊。为了更好的发挥这一特点，首先分析一下多普勒测速模糊的产生原因。

假设目标的径向速度为vt，则回波信号的频移为Δf=2fvt/（c+vt），c为水中声速，为了相邻频点不产生频谱混叠，则必须满足：

化简可得

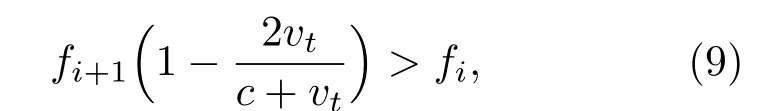
按照此方法得到常用的GC信号频点计算公式：

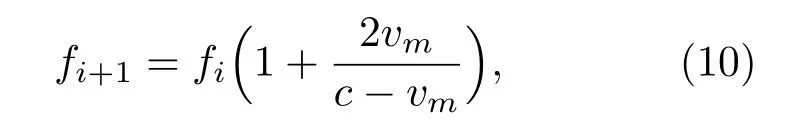
其中vm为系统可探测目标的最大径向速度，当目标的径向速度为v1时，其回波信号的频率为

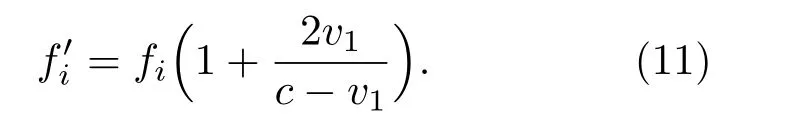
将（10）式带入（11）式，得到下一个频点的频率为

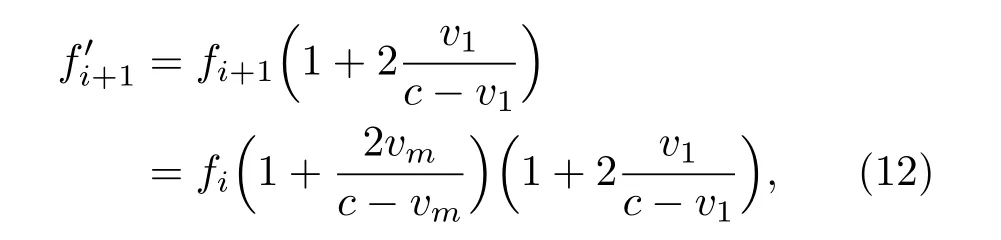
将（13）式带入（11）式，得到

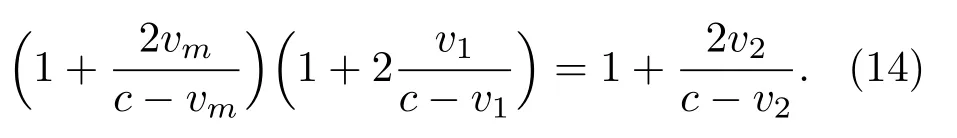
对（14）式进行化简有

由于声速远远大于目标速度，则有

从（16）式中可以看出，虽然这种设计方法避免了频谱混叠的情况，但回波频率将会与另一个速度的频点在产生大部分重叠。根据原有公式计算一帧GC信号，信号起始频率为f0=2 kHz，vm=25 m/s，频点数为13个，当目标速度分别为15 m/s与-10 m/s时，目标的回波信号如图3所示。

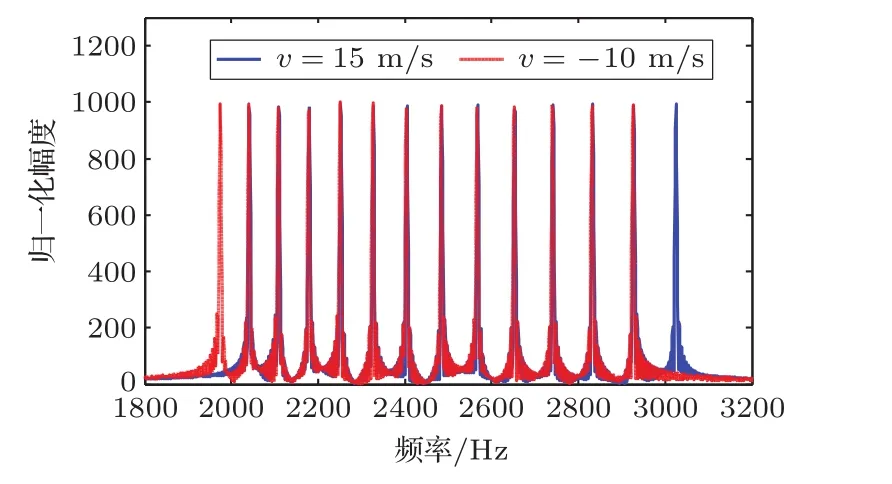
图3　不同径向速度的频谱Fig.3 The spectrum of different radial velocity

从图3中可以看出，目标径向速度分别为-10 m/s和15 m/s时，其频谱只有一个频点不重复，显然这样对于低信噪比条件下的速度估计是很不利的。想要防止这种情况的发生，通常是要进一步增大系统的速度容限，显然这会进一步浪费频带资源。

针对以上问题，利用在GC信号的频点计算公式中加入一组频率来降低频点的重合，具体的计算方法如下：

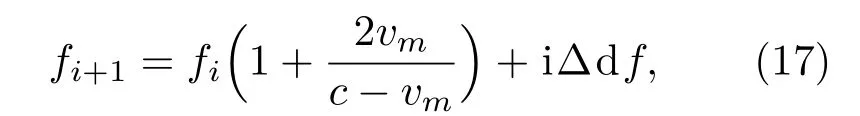
（17）式中，df就是抑制速度模糊的频率，其与系统的频率分辨率有关，频率分辨率越高，其值越小。根据公式（16）计算一帧GC信号，df=2 Hz，其余条件与之前相同，在目标径向速度分别为-10 m/s和15 m/s的时候，其回波频谱如图4所示。

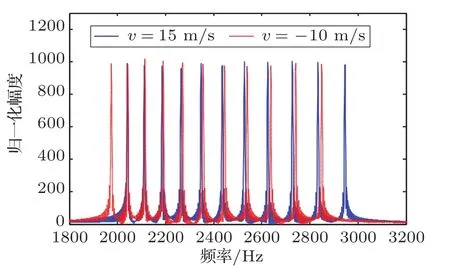
图4　不同径向速度的频谱Fig.4 The spectrum of different radial velocity

从图4中可以看出，通过加入这一组频率间隔，原重叠的频点已大部分分离，仅有个别频点仍旧重叠，在速度轴进行搜索时，虽然这些重叠的频点还会产生一个伪峰，但其已远远小于真值，很容易将其剔除。

4　仿真分析

仿真分析算法的有效性，信号的起始频率为2 kHz，最大速度容限为vm=20 m/s，频点数目为13个，信号脉宽为T=0.1 s，df=3 Hz，分别按传统方法以及修正的方法计算频点，得到两帧GC信号，记为S1与S2，信噪比为0 dB，目标径向速度为vt=10 m/s与vt=-15 m/s时，对接收信号进行多拷贝相关处理来进行速度估计，两帧信号的搜索结果如图5所示。

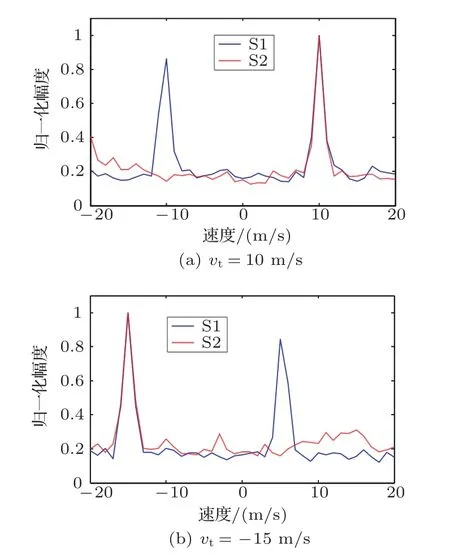
图5　噪声条件下的相关检测结果Fig.5 The correlation detecting result in noise

从图5中可以看出，按照传统方法设计的信号不但在目标真实速度处有一个相关峰值，在其相反方向上也有一个幅度非常高的相关峰值，而修正的信号设计方法只在真实速度处有一个相关峰值，在其它的速度值处虽然其输出也有一定的抖动，但其峰值均较小，基本不影响对目标速度的估计。

分析在混响限制条件下方法的有效性，混响信号按照以下方法计算［10］：各散射元相位均匀分布，幅度服从瑞利分布；声源静止，散射元的速度随即分布在（-5,5）m/s的区间，散射点为1000个。其余仿真条件与之前相同，信混比为-10 dB时，目标不同径向速度条件下的相关检测结果如图6所示。

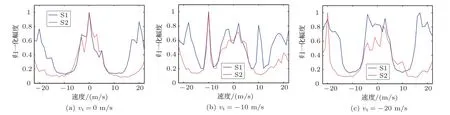
图6　混响条件下的相关检测结果Fig.6 The correlation detecting result in reverberation

从图6可以看出，由于强混响集中分布在低速区间，两个信号在vt=0 m/s处均产生较大的相关峰值，对于传统信号S1而言，由于频谱出现混叠，其在速度轴进行搜索时会出现很多幅度很高的伪峰，在速度较大时伪峰会将真实的时延峰淹没（如图6（c）所示），从而影响对目标的检测与速度估计，而对于信号S2而言，其在真实目标速度处会产生较尖锐的输出峰值，而在其它速度值处没有较明显峰值输出，虽然混响较强，仍可以进行有效的检测与速度估计。

5　结论

针对传统梳状谱信号容易出现多普勒频谱混叠的问题，文章分析了产生频谱混叠的原因，依照在不产生频谱混叠的前提下尽量节省带宽的原则，设计了一种几何梳状谱信号设计方法，通过改变传统的GC信号相邻频点间隔（加入一组抗混叠频率）来减小混叠速度测量频点的重合。仿真分析表明，相比于传统的GC信号，提出的信号设计方法有效的减小了多普勒频谱混叠的现象，在混响限制条件下具有更好的检测与估计性能。

［1］朱埜.主动声呐检测信息原理［M］.北京：海洋出版社，1990.

［2］蔡汉添.关于有源声呐检测最佳波形［J］.声学学报，1989，14（1）：45-50. CAI Hantian.On optimum signal for active sonar detection［J］.Acta Acoustica，1989，14（1）：45-50.

［3］田坦，刘国枝，孙大军.声呐技术［M］.哈尔滨：哈尔滨工程大学出版社，2004.

［4］COX H，LAI H.Geometric comb waveforms for reverberation suppression［J］.Proceeding of IEEE on Signals，Systems，and Computers，1994：1185-1189.

［5］ALSUP J.Comb waveforms for sonar［J］.Proceeding of IEEE on Signals，Systems，and Computers，1999：864-869.

［6］姚东明，蔡志明.主动声纳梳状谱信号研究［J］.信号处理，2006，22（2）：256-259. YAO Dongming，CAI Zhiming.Research on comb waveforms for active sonar［J］.Signal Processing，2006，22（2）：256-259.

［7］邓宇，李大芳，梅勇兵.多频率合成信号包络优化的初相搜索方法［J］.电讯技术，2008，48（3）：74-78. DENG Yu，LI Dafang，MEI Yongbing.Initial phase searching algorithm for optimizing multi-frequency compound signal envelop［J］.Telecommunication Engineering，2008，48（3）：74-78.

［8］张瑶.浅海条件下主动声呐目标探测若干方法研究［D］.哈尔滨：哈尔滨工程大学，2013.

［9］陈绍华，张忠波，汶宏刚，等.主动声纳SFM信号的抗混响性能分析［J］.声学技术，2011，30（3）：268-270. CHEN Shaohua，ZHANG Zhongbo，WEN Honggang，et al.Reverberation suppression ability of SFM signal in active sonar［J］.Technical Acoustics，2011，30（3）：268-270.

［10］URICK R.水声原理［M］.哈尔滨：哈尔滨船舶工程学院出版社，1990.

A comb signal design method that eliminated the speed ambiguity

LU Yang1YANG Jiageng1XUE Fei1ZHANG Yao2
（1 No.91439 Troop of the Chinese People's Liberation Army，Dalian 116041，China）
（2 Shenyang Institute of Automation，Chinese Academy of Science，Shenyang 110016，China）

Compared to the traditional signal，the comb spectrum signal has better reverberation suppression ability.But it is easy to produce Doppler velocity ambiguity.To solve this problem，this paper proposed a new waveform design method of geometric comb spectrum signal.By analyzing the reason of speed fuzzy，we add a set of anti-Doppler frequency interval to reduce the frequency coincidence based on conventional calculation method.Simulation results show that the proposed method can eliminate the spectrum overlap effectively.In noise and reverberation situation，this signal can get an obvious output peak，while avoiding the speed fuzzing. It has better detection performance than traditional comb spectrum signals.

Comb-spectrum signals，Doppler speed ambiguity，Signal design

TN911.6

A

1000-310X（2015）02-0158-05

10.11684/j.issn.1000-310X.2015.02.011

2014-05-13收稿；2014-10-05定稿

陆扬（1966-），男，江苏扬州人，高级工程师，研究方向：水声信号处理。

E-mail：cg300@sina.com