滤波器与随机共振结合检测微弱信号∗

范卫姣　王辅忠　张光璐

（天津工业大学理学院　天津　300387）

滤波器与随机共振结合检测微弱信号∗

范卫姣†王辅忠张光璐

（天津工业大学理学院天津300387）

基于双稳随机共振系统及滤波器的不同特性，本文提出了一种将两者结合起来检测微弱周期信号的方法，先用自适应前置滤波器对输入的弱周期信号及噪声进行滤波，再使其通过双稳随机共振系统，进而检测出弱信号。对比只有双稳随机共振的系统，仿真结果表明此时的输出信号中待测信号频谱幅度得到了很大的提高，且周围的干扰信号也得到了明显的削弱，即两者的结合使用可以更好的检测出微弱信号，这对强噪声背景下的信号检测有很强的实用性。

随机共振，滤波器，自适应，频谱幅度

1　引言

微弱信号检测的常规方法有频谱分析、相关检测、取样积分、小波分析理论等，这些方法都是通过抑制噪声来提高信噪比。1981年，意大利学者Benzi等提出了随机共振［1］的概念，之后，随机共振在微弱信号检测方面得到了较大的发展。与各种抑制噪声的方法不同，它是充分利用噪声来增强弱信号能量以提高信噪比，达到识别弱信号的目的［2］。

双稳系统是研究随机共振时常用的一种非线性系统，噪声通过双稳系统后其能量向低频区集中，根据绝热近似理论，只有在噪声能量集中的低频区域才能产生随机共振主谱峰，高频区的噪声对随机共振的发生贡献甚微［3］。滤波器能将某些频率的信号或噪声滤除，考虑此特点，本文将滤波器与双稳系统结合起来进行弱信号检测，仿真结果表明，输出信号中待测信号频率处的频谱幅度有了很大的增长，提高了待测信号的检测率。

2　随机共振检测的基本原理及模型

随机共振是微弱周期信号、噪声及非线性系统三种基本要素协同作用下产生的一种非线性动力学现象，当三者达到某种匹配关系时，在周期信号频率处可发生随机共振，从而检测出微弱信号［4］。朗之万方程（Langevin）描述的非线性双稳系统是研究随机共振的经典模型：

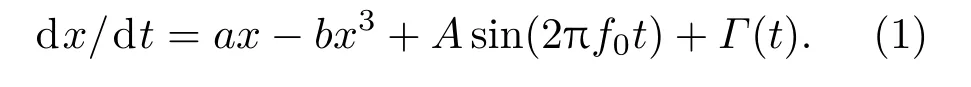
式中，a、b是双稳系统参数且a＞ 0，b＞ 0，Asin（2πf0t）是幅度为A、频率为f0的待测弱周期信号，为高斯白噪声，D是噪声强度，且满足统计平均：

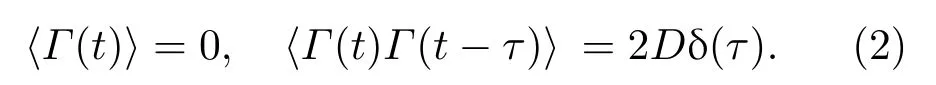
式（1）描述了粒子同时受到弱周期信号和噪声驱动时，在双势阱中的过阻尼运动［5］。

当没有输入弱周期信号和噪声，即A=0，D=0时，非线性双稳系统可用其势函数V（x）=-ax2/2+bx4/4表示，系统有两个相同的势阱，阱底位于势垒高为Δv=a2/4b，最终输出状态将停留在两个势阱中的任意一个，取决于系统的初始状态；当输入弱周期信号时，双稳系统的平衡被破坏，双稳态势曲线发生周期性倾斜，但只要A处于临界值AC以下粒子只能在某一侧势阱内以信号频率进行局域的周期运动；然而，当系统引入噪声且噪声强度为某一合适值时，粒子在两势阱间的跃迁速率将与微弱周期信号同步，表现为输出信号具有良好的周期性，噪声得到了一定的抑制，输出信号频谱在弱周期信号频率处得到有效的放大。经过双稳随机共振系统后，输出信号频谱由两部分组成［5］：

其中S1（f）是由微弱周期信号引起的，与周期信号同频；S2（f）由噪声引起，具有洛伦兹分布形式，即频谱能量向低频区域集中［6-7］，因此，能够产生随机共振谱峰的频带，将局限在系统输出的低频段，所以考虑在经过双稳随机共振系统前把一些不必要的高频噪声滤除掉。

滤波器的功能是允许一部分频率的信号顺利通过，而另外一部分则受到较大的抑制，因此我们将滤波器加入双稳随机共振系统中，让前置滤波器先将高频部分的噪声过滤，微弱周期信号与噪声在经过双稳随机共振系统时就减少了高频噪声的干扰，从输入端改善信号质量，从而进一步改善输出信号，增强系统对微弱信号的检测能力。

3　滤波器的设计及参数选择

FIR数字滤波器因具有严格的线性相位、运算稳定且速度快［8］，得到了广泛应用，在众多的设计方法中，等波纹逼近法为一种最优化设计［9］，其特性如图1所示：

图1　等波纹低通滤波器频谱图Fig.1　Spectrum diagram of equal-ripple lowpass filter

一个等波纹低通滤波器的参数包括通带截止频率fpass、阻带截止频率fstop、通带最大衰减系数rp及阻带最小衰减系数rs。我们借助Matlab信号处理工具箱，简单调用函数remezord和remez就可以完成线性相位FIR数字滤波器的等波纹最佳逼近设计。通带与阻带截止频率的选择影响着信号的滤波质量，所以首先用Matlab程序确定最佳的通带截止频率fpass及阻带截止频率fstop，流程图如图2。

图2　滤波器最佳参数选择流程图Fig.2　The flow chart of optimal parameter selection

具体步骤如下：

（1）将周期信号与噪声输入系统中，根据待测信号频率确定滤波器的初始参数：通带截止频率fpass及阻带截止频率fstop；

（2）在初始fpass值下以固定步长不断改变fstop的值，观察每一组参数下输出信号中待测信号频率处的频谱幅度，并将最大值及其对应的fpass，fstop记录下来；

（3）以固定步长改变fpass，重复步骤（2）；

（4）从记录的一组待测信号频谱幅度值中找出最大值，此时所对应的fpass，fstop就是滤波器的最佳参数。

4　加滤波器的随机共振模型简介

图3为添加滤波器后的双稳随机共振系统Simulink模型。Sine Wave产生微弱周期信号，Band-Limited White Noise模块产生白噪声，两者相加后通过Digital Filter Design模块，它是Matlab信号处理工具箱专用的滤波器设计分析工具，可以随时调整滤波器类型及参数，滤波结果实时显示在图形区，有利于滤波器的进一步优化。将经过滤波器以后的信号输入双稳系统，a、b参数的值由自适应LMS算法算出［10］，输入到仿真模型中。Math Function产生x的平方项，再经过Product模块，乘以常数b，形成郎之万方程中的-bx3项。将-bx3、ax与经过滤波器以后的输入信号经过加法器Add1、积分器Integrator，就可得到输出信号x，在Scope中显示输出信号的时域波形，To Workspace模块把输出信号的数据导出到Workspace中，然后在Matlab中经傅里叶变换后画出输出信号的频谱图。

图3　加滤波器的随机共振系统Simulink仿真模型Fig.3 Simulink model of combination filter with stochastic resonance

我们利用上面提到的Matlab程序计算出滤波器的最佳参数，然后将其输入到图3的Digital Filter Design模块中，运行Simulink仿真模型，得到输出信号的频谱图，并对其进行分析。

5　实验仿真结果及分析

选取微弱周期信号的幅度A=0.3，采样频率fs=5，噪声强度D=0.8，并以系统输出的信噪比为衡量标准，用LMS算法对双稳随机共振系统参数进行最优化处理［10］，可得到系统的参数为a=0.69，b=0.6时输出信号的信噪比最大，故以此值作为双稳系统的参数，让频率为f0=0.005，0.01，0.015，0.025 Hz的周期信号分别通过低通滤波器与双稳系统组成的复合系统，得到了对应低通滤波器的fpass， fstop最优参数列表，如表1所示。

我们以f0=0.005 Hz为例，将a=0.69，b=0.6，fpass=0.021 Hz，fstop=0.098 Hz输入到图3所示的仿真系统中，观察此频率下的周期信号加噪声通过复合系统后的频谱变化情况。

图4为三种输出信号的时域及频域图，从图4（c）可以看出，当周期信号与噪声通过低通滤波器与双稳系统的复合系统后，可看出明显的周期性，且此时的输出信号边缘较为光滑，图4（f）为对应的输出信号频谱图，从图4（f）中可以看出，在待测信号频率f0=0.004999 Hz处出现了明显的谱峰，幅度为y=2659，比只经过双稳随机共振系统时增加了约137%，而且此时的频谱图高频部分的干扰信号明显减少。由此可见，在双稳随机共振系统中加入滤波器的复合系统，可大大提高系统检测微弱信号的能力。下面再从输入噪声频率分布的角度进行分析。

表1　不同信号频率下滤波器的最佳参数Table 1 Optimal parameter for different signal frequency

图4　时域图（a）、（b）、（c）；频域图（d）、（e）、（f）Fig.4 Time-domain（a）（b）（c）；Frequency-domain（d）（e）（f）

图5为D=0.8的白噪声在不同情况下的频谱分布，从图5（c）可以看出，白噪声经过低通滤波器后，高频部分的能量被滤除，图5（d）为通过低通滤波器加双稳系统的复合系统后的频谱分布，此时的噪声能量更加集中在低频区，且低频成分的能量值相对于图5（b）有了很大的增加，待测信号频率周围的噪声能量大大增加，所以能更好的激励出随机共振现象，表现为输出信号中待测信号频率处的幅度提高。

从表1中观察发现，周期信号与噪声通过复合系统后，待测信号频率处的频谱幅度比只有双稳随机共振系统时有所提高，但随着周期信号频率的增大，其增加幅度逐渐变小。这是因为当周期信号频率较大时，噪声能量依然处在低频区，待测信号频率周围可利用的噪声较少，所以频谱幅度的增加不如低频信号时明显。以f0=0.025 Hz为例，观察噪声在表1参数条件下通过低通滤波器与双稳系统的复合系统后的频谱分布，如图6所示。

图5　D=0.8的白噪声在不同情况下的频谱分布Fig.5 The white noise spectrum distribution at different circumstances for D=0.8

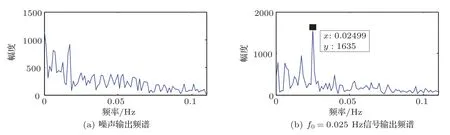
图6　经过低通滤波器与双稳系统的复合系统后的频谱分布Fig.6 Frequency spectrum distribution after low-pass filter with bistable system

从图6（a）可以看出，噪声通过此复合系统后，频谱能量主要集中在0～0.02 Hz之间，图6（b）为f0=0.025 Hz的周期信号与噪声通过此复合系统后的输出信号频谱图，在待测信号频率处可以看到明显的谱峰，其值为y=1635。与只经过双稳随机共振系统相比，幅值增加了15%，增加幅度较小，且低频处有明显的干扰信号。我们考虑用带通滤波器代替低通滤波器，先将一部分低频噪声滤除，再经过双稳随机共振系统后，低频区的噪声能量会有很大的减少。设置带通滤波器的参数如下：fs=5，fstop1=0.005，fpass1=0.025，fpass2=0.3，fstop2=0.32，则噪声通过此带通滤波器跟双稳随机共振系统的复合系统后，其输出频谱如图7所示。

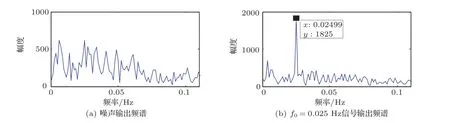
图7　经过带通滤波器与双稳系统的复合系统后的频谱分布Fig.7 Frequency spectrum distribution after band-pass filter with bistable system

图7（a）为噪声通过带通滤波器与双稳随机共振系统的输出频谱，与图6（a）对比可以发现，加带通滤波器后，低频区的噪声能量得到了明显的削弱，依然将f0=0.025 Hz的周期信号与噪声输入新的复合系统，得到输出信号的频谱图7（b），从图中可以看出，待测信号的频谱幅度为1825，比低通滤波器时增加了11%，比只有双稳随机共振系统时增加了29%。即信号频率较高时，加带通滤波器比低通滤波器能得到更明显的效果，这是因为加带通滤波器后减少了低频区的噪声能量，对在待测信号频率处发生随机共振的干扰也就减小，进而增大了待测信号的频谱幅度。说明发生随机共振时待测信号只能利用其周围较窄频率内的噪声能量，当信号频率较大时，噪声依然处在低频区，信号频率周围可利用的噪声较少，所以发生随机共振的现象不如低频时明显。

6　结论

本文充分考虑滤波器及双稳随机共振系统的特性，提出了一种将两者结合起来检测微弱信号的方法。仿真结果表明：

（1）当信号频率低于0.02 Hz时，采用低通滤波器可减少高频噪声的干扰，待测信号频谱幅度比只有双稳随机共振系统时可提高30%～140%左右；

（2）当信号频率高于0.02 Hz时，带通滤波器能更好的实现弱信号的检测，以f0=0.025 Hz为例，将带通滤波器与双稳随机共振结合起来，待测信号频谱幅度比只有双稳随机共振系统时提高了30%；

（3）发生随机共振时，待测信号只能利用周围较窄频率内的噪声能量，当信号频率较高时，低频噪声会影响随机共振的效果，削弱低频噪声能量，可以提高待测信号频率处的频谱幅度。

由此可见，将滤波器与双稳随机共振系统相结合，通过适当选择滤波器的类型，自适应调节其参数，可大大改善待测信号的频谱幅度，这就提高了系统检测微弱信号的能力，可用于强噪声背景中的弱信号检测。但此方法目前只适用单个的低频周期信号，当信号频率较高时，随机共振的效果不如低频时明显；当有多个周期信号输入时，滤波器参数的自适应将会增加难度，需要进一步的研究验证。

［1］BENZI R，PARISI G，STUEM A.A theory of stochastic resonance in climatic change［J］.SIAM Journal on Applied Mathematics，1983，43（3）：565-578.

［2］HARI V N，ANAND G V，PREMKUMAR A B.Stochastic resonance phenomenon in an underdamped bistable system driven by weak asymmetric dichotomous noise［J］. Signal Processing，2012，92：1745-1757.

［3］孟玲玲，刘小娜.不同类型噪声作用下的随机共振［J］.真空电子技术，2011，（5）：28-31. MENG Lingling，LIU Xiaona.Different kinds of noise under the action of stochastic resonance［J］.Vacuum Electronics，2011，（5）：28-31.

［4］LONG F，WEI G，MEI D C.Stochastic resonance induced by bounded noise and periodic signal in an asymmetric bistable system［J］.Physica A，2012，391（22）：5305-5310.

［5］夏均忠，刘远宏，马宗坡.基于调制随机共振的微弱信号检测研究［J］.振动与冲击，2012，31（3）：132-135. XIA Junzhong，LIU Yuanhong，MA Zongpo.Research of weak signal detection basing on modulated stochastic resonance［J］.Vibration and Shock，2012，31（3）：132-135.

［6］岳建海，曾凡仔，裘正定.双稳系统噪声特性的分析与弱信号检测的研究［J］.计量学报，2005，26（1）：60-65. YUE Jianhai，ZENG Fanzi，QIU Zhengding.Analyis of the characteristics of the bistable system noise and research of weak signal detection［J］.Acta Metrologica Sinica，2005，26（1）：60-65.

［7］LENG Y G，WANG T Y，GUO Y.Engineering signal processing based on bistable stochastic resonance［J］.Mechanical Systems and Signal Processing，2007，21：138-150.

［8］韦鹏.基于Matlab窗函数法辅助设计FIR滤波器［J］.电脑知识与技术，2012，8（18）：4564-4566. WEI Peng.Designing FIR filter based on Matlab window function method［J］.Computer knowledge and technology，2012，8（18）：4564-4566.

［9］陶国彬，张秀艳，任玉霞.FIR滤波器的等波纹最优化设计［J］.大庆石油学院学报，2007，31（6）：105-107. TAO Guobin，ZHANG Xiuyan，REN Yuxia.Equiripple optimal design of FIR filter［J］.Journal of Daqing Petroleum Institute，2007，31（6）：105-107.

［10］GAO Y X，WANG F Z.Adaptive cascaded-bistable stochastic resonance system research and design［J］.Computational and Theoretical Nanoscience，2013，10：1-5.

Detecting weak signals by combining stochastic resonance with filter

FAN WeijiaoWANG FuzhongZHANG Guanglu
（College of Science，Tianjin Polytechnic University，Tianjin 300387，China）

Making full use of the characteristics of stochastic resonance and filter，an adaptive system to detect weak signals by combining them is designed in this paper.An adaptive pre-filter is used to first filter input signals and noise，and then make them pass the bistable SR system.The simulation results show that the spectrum amplitude of output signal has been greatly improved compared with the one that only has filter or bistable SR system.This indicates the combination of the two can well detect the weak signals，so it is practicability for detecting the weak signals embedded in strong noise.

Stochastic resonance，Filter，Self-adaptation，Spectrum amplitude

O324

A

1000-310X（2015）02-0169-06

10.11684/j.issn.1000-310X.2015.02.013

2014-05-30收稿；2014-08-26定稿

∗国家自然科学基金项目（61271011）

范卫姣（1988-），女，硕士研究生，研究方向：微弱信号检测。

E-mail：fanweijiao1988@163.com