利用宽带引导声源重构拷贝声场的目标声源定位∗
姚美娟 马 力 鹿力成 郭圣明
(1中国科学院声学研究所 北京 100190)
(2中国科学院水声环境特性重点实验室 北京 100190)
(3中国科学院大学 北京 100049)
利用宽带引导声源重构拷贝声场的目标声源定位∗
姚美娟1,2,3†马 力1,2鹿力成1,2郭圣明1,2
(1中国科学院声学研究所北京100190)
(2中国科学院水声环境特性重点实验室北京100190)
(3中国科学院大学北京100049)
为了避开传统的匹配场目标定位技术对环境先验知识的依赖性,提出了在均匀浅海环境中只知道少量环境参数的情况下,利用垂直接收阵和不同距离上的两枚宽带引导声源重构声场对目标声源进行定位的一种方法。这种方法主要基于简正波估计和声场重构两种关键技术,同时省去了匹配场定位技术中大量的拷贝声场计算。数值仿真主要采用线性Bartlett匹配处理器分析了目标定位效果,在信噪比高于10 dB的情况下,定位效果良好。
引导声源,简正波估计,声场重构,目标定位
1 引言
由于复杂的声环境使得声纳技术受到明显制约,目标定位技术在水声研究领域中受到越来越多的关注。传统的匹配场处理技术(Matched field processing,MFP)出现于上世纪80年代,在目标探测和三维定位等方面的应用取得了很大进展,大大推动了被动声纳技术的发展。但匹配场技术对环境参数和声场模型的依赖性极高,容易受到环境参数和声场模型失配的影响。为了克服匹配场定位技术的不足,减少定位效果对海洋环境参数失配和声场模型失配的影响,人们力求寻找一种新的不需要精确的海洋环境先验知识的定位技术。“虚拟接收”的概念于上世纪90年代末出现于水声学中,它通过对垂直阵接收到的未知目标声源和已知引导声源信号的相关处理,来得到在引导声源位置处对未知声源的虚拟接收声场,从而消除原先垂直接收阵和未知声源之间的海洋环境变化影响。Martin Siderius等人利用虚拟接收的概念,研究了浅海环境中的多途补偿问题,适当调节引导声源的位置,可以在很大程度上消除垂直接收阵和虚拟接收阵之间的环境影响[1]。引导声源的引入达到了对垂直接收阵和引导声源之间的海洋环境未知补偿效果。当存在引导声源时(在实际使用中,引导声源一般选取为人为布放声源或者机会声源),可以有多种途径来实现声源定位:(1)根据垂直阵接收到的引导声源声场反演得到所需要的海洋环境参数,再利用声场算法模型计算得到拷贝声场,进行匹配声场定位,同时给出目标声源的距离和深度估计;(2)利用文献[1]等所给的虚拟接收技术,结合虚拟声场在频率-频率偏移平面上的干涉条纹或者直接分析实际声场在频率-距离平面上的干涉条纹来获得目标声源距离估计,这种方法原则上不能直接得到目标声源深度;本文中将提出一种新的基于简正波分离技术和声场重构技术的目标定位技术。利用声场重构技术与前面所述的与第一种方法相比,可以节约甚至避免拷贝声场计算过程,与第二种方法(虚拟接收技术)相比,可以同时给出声源距离和深度估计。
声场重构技术是一种新颖的水声学技术,启发于S.C.Walker[2]等人提出时间反转聚焦在深度上的偏移,主要从声场位置信息和声场相位信息两个方向重构声场。基于声场重构技术的目标定位技术,首先从引导声源接收声场中估计简正波模态函数。近年来,随着人们对水声信道认识的加深和信息处理技术的发展,水声简正波分离技术得到了发展,Westwood等人提出了在没有任何先验信息的条件下,利用垂直线列阵(Vertical line array,VLA)测量到的声压数据,可以直接提取简正波的信息[3]。Kuperman等人利用相同的方法,通过处理环境噪声的VLA数据提取了简正波的信息,并且提出了在已知声速剖面的条件下,利用打靶法得到水平波数[4]。在提取得到简正波模态函数的基础上重构得到拷贝声场,再结合传统的匹配场处理方法进行目标声源定位。
2 理论方法
2.1匹配场声源定位
传统的匹配场定位方法,是利用已知的(或反演获得的)海洋环境参数信息,基于声信号多途传播特点采用传播模型来计算拷贝声场(向量),并与实际的阵接收声场(向量)进行“匹配”,来实现对目标声源的定位。目前主要采用的匹配场处理算法,按照其权向量是否依赖测量数据,可以划分为线性和自适应匹配场处理两大类[5]。垂直接收阵匹配场处理的线性Bartlett处理器的输出为

其中R(rs,zs)是估计得到的目标声源阵接收声场po的互谱密度矩阵,权系数v(r,z)取拷贝声场向量p(r,z),上角标符号H表示向量的共轭转置,(r,z)是目标声源定位空间搜索点位置。在真实声源位置(rs,zs)处D(r,z)取最大值,从而决定出目标声源位置。可以看到,对于传统的匹配场声源定位来说,关键性的工作就是如何从接收声场中估计得到互谱矩阵以及如何计算拷贝声场。
拷贝声场计算,可以在海洋环境参数已知的情况下,利用合适的声场算法模型来计算得到的,也可以利用接收到的已知声源信号,来估计海洋环境参数或者是拷贝声场计算直接可用的简正波参数(包括简正波本征值、本征函数和衰减系数等)。相比较而言,前者容易受到环境参数和声场算法模型不准确性的影响,引起失配问题,并且通过模型计算匹配声场也有相当大的计算量;后者直接从现场数据中提取所需要的环境参数信息或者是声场计算所需要的简正波参数,尽管也会存在参数提取不准确性的失配可能,但可以很大程度上降低这种风险,并且可以显著降低匹配声场计算量甚至于不需要直接计算。
2.2利用声场重构技术的拷贝声场计算
声场重构技术是一种新颖的水声学技术,利用声场重构技术的拷贝声场计算以及进一步的目标声源定位,得益于S.C.Walker[2]等人提出的时间反转聚焦在深度上调焦技术的启发,类似于用测量的拷贝声场来进行匹配场定位,具有较好的宽容性。
注意到在水平分层介质中,垂直阵接收时拷贝声场(向量)计算可以写成

其中本征函数矩阵Φ和声源位置信息的系数向量b分别为
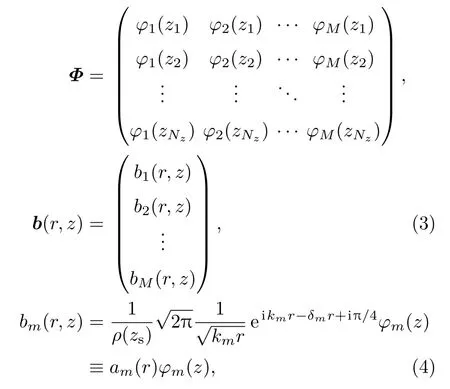
zn是垂直接收阵阵元深度,km和δm分别为简正波本征值和衰减系数。可以知道,只要能够从参考声源接收声场中提取得到本征函数矩阵Φ,再重构出不同空间位置(r,z)处系数bm(r,z)或am(r),就可以方便的重构得到所需要的拷贝声场向量p(r,z)。
2.2.1简正波本征函数获取
在有引导声源的情况下,从垂直阵接收到的宽带引导声源声场中就可以提取得到对应的简正波本征函数。
对垂直接收阵接收得到的引导声源时域声压信号序列作离散傅里叶变换,得到频域的复声压信号,然后取某一窄带(ω1:ωNω)范围内不同深度的复声压组成矩阵

Sg(ωj)和zg分别是引导声源频谱和深度,zi(i=1,2,···,Nz)对应Nz个不同的垂直阵接收水听器深度,km、δm和φm(z)分别是第m号简正波的水平波数、衰减系数和本征函数。
简正波本征函数φm(zi|ω)原则上也是频率的函数。当频带范围(ω1:ωNω)比较窄时,简正波本征函数变化不大,可以认为是与频率无关的常量,φm(zi)。这样注意到简正波本征函数的正交归一化特性,它相当于是矩阵Q中列向量的一组正交基函数。为了获得这组正交基函数,对矩阵Q作SVD分解有

在垂直阵满阵接收的情况下,V是与简正波系数相关的矩阵,容易知道正交矩阵U的列向量与各号简正波本征函数是成比例[6],由此这样我们就可以构造出所需要的简正波本征函数矩阵Φ。当垂直阵不是满阵时,由于简正波本征函数在接收阵覆盖深度范围不是完全正交的,不能如(8)式这样简单的换算获得,需要采用更为精致的方法。
2.2.2声场重构技术计算拷贝声场
获得简正波本征函数矩阵Φ之后,再利用简正波分解技术,可以从引导声源接收声场中提取得到对应的简正波系数

其中ω∈[ω1:ωNω],

宽带参考声源一般可以选取所在海区的水面船只,距离和深度都是能够获得作为已知参数。这样首先从提取得到的本征函数矩阵Φ,插值得到参考声源深度和拷贝声场计算深度上的本征函数值φm(zg)和φm(z),再结合(9)式对接收声场的简正波分解结果换算得到

注意到
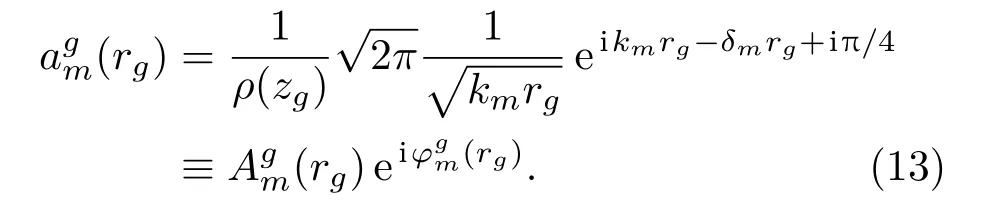
利用两个不同距离rg1,rg2上接收到的参考声源声场(暂时认为参考声源深度是一样没变化的),可以构造出

以及

结合前面提取到的本征函数矩阵之后,不难写出所需的拷贝声场矢量

得出拷贝声场向量后,代入(1)式就可得到定位结果。注意声场重构过程中的源信号谱级差异等方面引入的常系数比例系数差异,并不会影响到最后的匹配场定位结果(因为有归一化处理)。
鉴于搜索点(r,z)空间网格点不宜太粗,这样要求两个引导声源距离点差值Δr不要太大,要满足网格点间距要求。
3 数值计算
3.1环境模型介绍
至少需要两枚宽带引导声源对目标声源声场进行重构。如图1是利用宽带引导声源重构声场对目标声源进行定位的水声环境模型示意图。垂直阵接收到来自于引导声源1,2以及目标声源的声信号,利用垂直阵接收到的引导声源1,2的声信号对目标声源处的声场进行重构。声速剖面如图1中所示,各水声参数如表1中所示。

图1 水声环境模拟示意图Fig.1 Sketch of underwater acoustic environment for simulation

表1 仿真环境水声参数Tabel 1 Underwater acoustics parameters of the simulation
3.2数值计算结果分析
利用宽带引导声源进行SVD分解估计简正波函数时,选用宽带引导声源的频率段为210~250 Hz,对此宽带声场进行SVD分解,每隔1 Hz计算一次以估计简正波模态函数;同时在中心频率230 Hz下直接计算得到简正波模态函数,将这两者进行比较以验证所估计的简正波模态函数的准确性。当引导声源深度处于某号简正波的节点时,该号简正波不能被激发出来,所以将引导声源近海面布放。引导声源1和引导声源2布放的位置分别为(11 km,3.5 m)和(10 km,3.5 m),目标声源位置(18 km,18 m)。这里看到引导声源1,2以及目标声源距离之间的关系为r-rg1=7∗(rg1-rg2);利用SVD分解方法估计简正波本征函数时,声场要满足远场条件,这里在较远距离处(15 km,3.5 m)放置一枚宽带引导声源以估计简正波模态函数。
如图2,虚线的简正波模态函数是直接计算的结果,实线的简正波模态函数是利用宽带引导声源进行SVD分解的估计结果,实线与虚线几乎完全吻合,完美的验证了利用宽带引导声源进行SVD分解方法提取简正波的理论。简正波估计准确,是后续声场重构以进行目标声源定位的前提。

图2 未加噪声时简正波模态函数Fig.2 Normal mode function with no noise
利用提取的简正波函数以及垂直阵接收到的引导声源1,2的声场信息的衰减和相位变化重构声场,再将重构声场与目标声源声场匹配从而对目标声源进行定位。如图3是线性Bartlett处理器输出模糊度平面图和surf立体图。标注“o”符号的位置为目标声源的真实位置(18 km,18 m),模糊度平面中标注“+”符号的位置为线性Bartlett处理器的输出峰值为(17.8 km,19 m),处理器输出结果为水平距离定位误差为1.11%,深度上定位误差3.33%,定位效果良好。

图3 未加噪声时线性Bartlett处理器目标定位结果Fig.3 Linear Bartlett processor localization results with no noise
在实际应用中,垂直接收阵接收到的声场都含有一定的噪声场,下面将引导声源与目标声源的声场中均加入信噪比为15 dB的噪声,分析目标定位结果。如图4,噪声的干扰使SVD分解方法提取得到的简正波模态函数与真实的模态函数值之间有一定的偏差。如图5,目标声源真实位置为(18 km,18 m),自适应匹配处理器的输出峰值位置为(18.3 km,19 m),处理器输出结果为水平距离定位误差为1.67%,深度上定位误差为3.33%,定位效果良好。

图4 信噪比为15 dB简正波模态函数Fig.4 Normal mode function with 15 dB signalto-noise-ratio
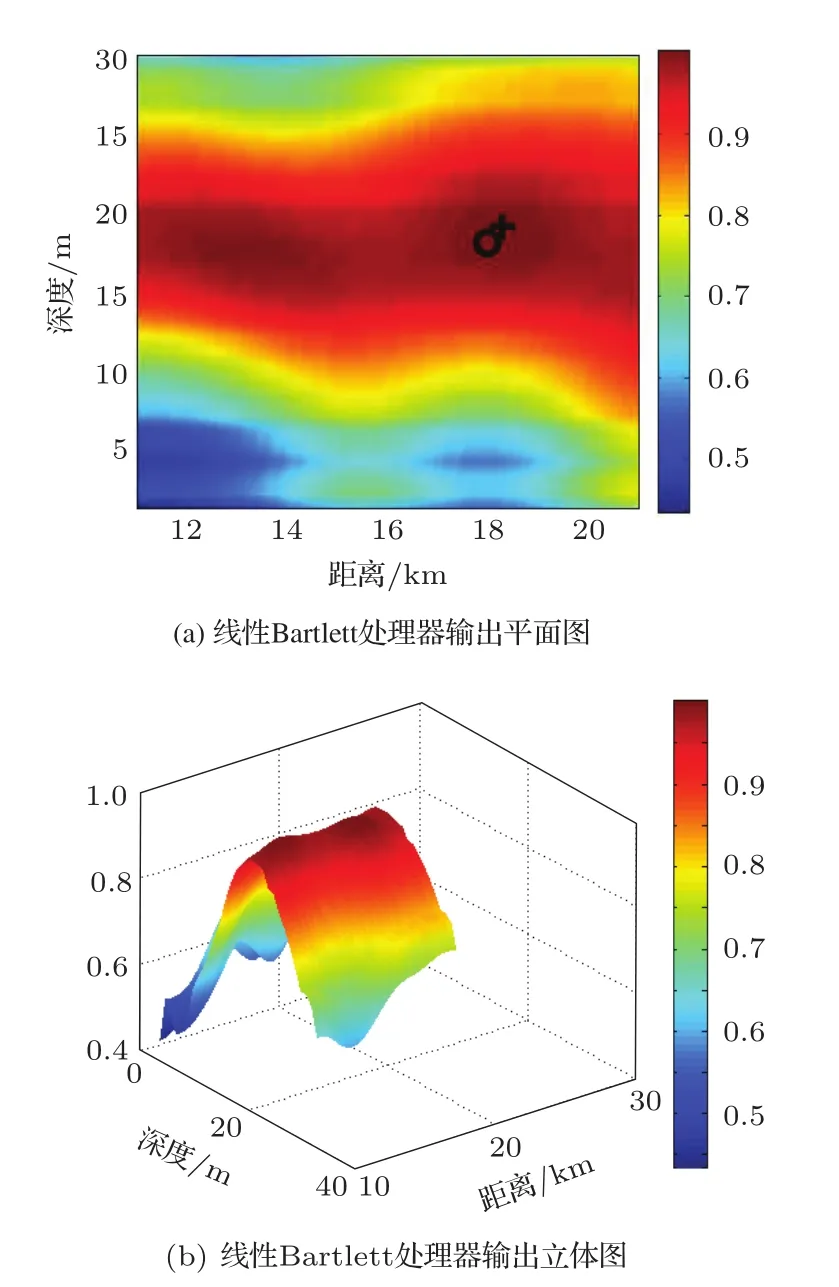
图5 信噪比为15 dB时线性Bartlett处理器目标定位结果Fig.5 Linear Bartlett processor localization results with 15 dB signal-to-noise-ratio
声场中噪声的加入对简正波模态获取和目标定位都产生了一定的影响,将引导声源与目标声源的声场中的信噪比降低至10 dB,下面分析目标定位结果。
如图6,信噪比的降低使SVD分解方法提取得到的简正波模态函数与真实的模态函数值之间的偏差进一步增大(相对于图4)。因此由提取的简正波模态函数重构得到的声场与真实声场间的偏差也将进一步增大,这必然增加定位的误差,如图7,线性Bartlett处理器的输出峰值位置为(18.4 km,20 m),处理器输出结果为水平距离定位误差为2.22%,深度上定位误差为6.67%,信噪比的降低使得定位误差变大。
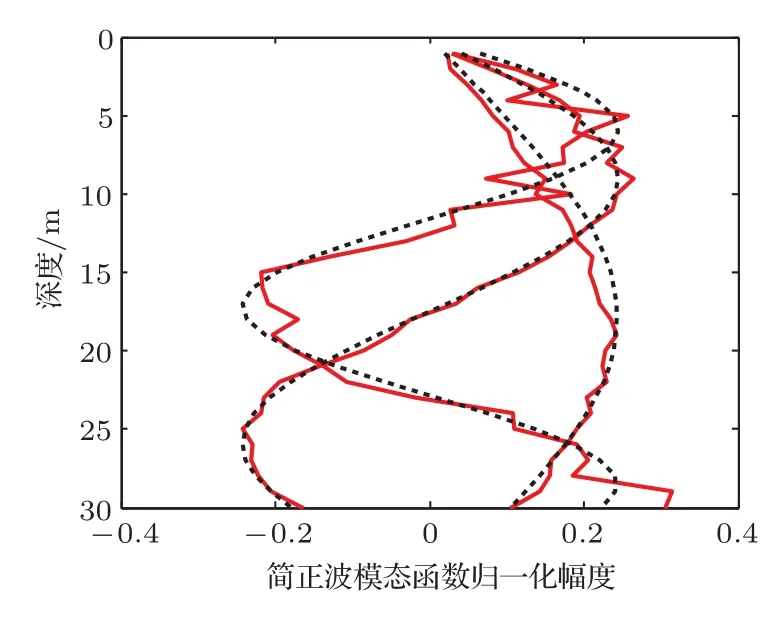
图6 信噪比为10 dB时简正波模态函数Fig 6 Normal mode function with 10 dB signalto-noise-ratio
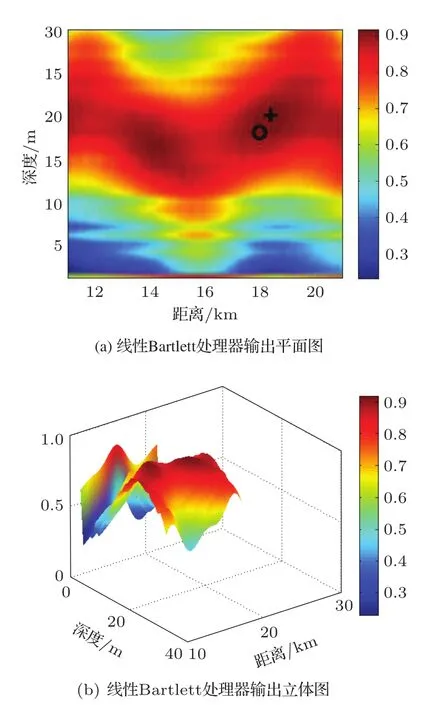
图7 信噪比为10 dB时线性Bartlett处理器目标定位结果Fig.7 Linear Bartlett processor localization results with 10 dB signal-to-noise-ratio
4 结论
利用宽带引导声源重构拷贝声场进行目标定位的方法,主要基于简正波获取技术和声场重构技术两种关键技术。它与传统的匹配场定位技术相比具有可以省去匹配声场建模和大量声场计算的优势,与利用虚拟接收方法估计声场干涉条纹的斜率对目标测距的方法相比可以同时给出目标声源的距离和深度。本文通过仿真实验,分析了在浅海海域中利用两枚宽带引导声源进行目标定位的效果。在信噪比为10 dB以上的情况下,水平距离定位误差和深度定位误差在5%到10%左右,定位效果良好。随着信噪比的降低,定位误差会增大,下一步工作将研究如何在较低信噪比下获得较好的定位效果。另外,声场重构技术中相位信息的获取在工程应用中受到限制,这也是下一步工作的方向。
[1]SIDERIUS M,JACKSON D R,ROUSEFF D,et al.Multipath compensation in shallow water environments using a virtual receiver[J].J.Acoust.Soc.Am.,1997,102(6):3439-3449.
[2]WALKER S C,ROUX P,KUPERMAN W A.Focal depth shifting of a time reversal mirror in a rangeindependent waveguide[J].J.Acoust.Soc.Am.,2005,118(3):1341-1347.
[3]NEILSEN T B,WESTWOOD E K.Extraction of acoustic normal mode depth functions using vertical line array data[J].J.Acoust.Soc.Am.,2002,111(2):748-756.
[4]HURSKY P,HODGKISS W S,KUPERMAN W A. Extracting modal structure from vertical array ambient noise data in shallow water[J].J.Acoust.Soc.Am.,1995,98(5):2971.
[5]杨坤德.水声阵列信号的匹配场处理[M].西安:西北工业大学出版社,2008:165-166.
[6]ZHAO Zhendong,WANG Ning,GAO Dazhi,et al. Broadband source ranging in shallow water using the Ω-interference spectrum[J].Chin.Phys.Lett.,2010,27(6):064301-1-064301-4.
Object source localization using the broadband guide source to reconstruct the replica field
YAO Meijuan1,2,3MA Li1,2LU Licheng1,2GUO Shengming1,2
(1 Institute of Acoustics,Chinese Academy of Sciences,Beijing 100190,China)
(2 Key Laboratory of Underwater Acoustics Environment,Chinese Academy of Sciences,Beijing 100190,China)
(3 University of Chinese Academy of Sciences,Beijing 100049,China)
A new method of object source localization,on the condition that a few environment parameters are known in range-independent shallow water environment,by using the vertical receiver array and the broadband guide source to reconstruct acoustic field,is presented to avoid the strong dependence on environment parameters of traditional matched field processing localization technique.This method is mainly based on normal modes estimation technique and acoustic field reconstruction technique and also can avoid the complicated computation of replica field for matched field processing localization.Linear Bartlett processor is used to analyze the simulation results.Desired results are obtained when the signal-noise ratio is higher than 10 dB. Key wordsGuide source,Normal mode estimation,Acoustic field reconstruction,Source localization
O427.1
A
1000-310X(2015)02-0135-07
10.11684/j.issn.1000-310X.2015.02.007
2014-05-08收稿;2014-09-15定稿
∗国家自然科学基金项目(10774156)
姚美娟(1988-),女,山东临沂人,博士研究生,研究方向:声学。
E-mail:yyyshui@126.com

