三角函数有理式的一种简单积分法
邓敏(湖南交通职业技术学院,长沙 410004)
三角函数有理式的一种简单积分法
邓敏
(湖南交通职业技术学院,长沙410004)
本文通过分析、解答几种具有代表性的三角函数有理式不定积分问题,介绍了一种求三角函数有理式不定积分的简单方法——关联辅助积分法。
三角函数有理式积分关联辅助
求三角函数有理式的不定积分是高等数学中一种常见的、重要的积分问题,但是没有一种统一的积分方法适用于所有情形的三角函数有理式积分,其积分方法非常灵活,也非常多,常用的有凑微分法、换元积分法(万能代换法)、分部积分法、待定系数法等,特别常用的是万能代换法。但是,对很多三角函数有理式的积分,如采用以上所述的常规方法来求,一般过程很繁琐,有的题甚至无法求出。学生往往对此类积分问题望而生畏,敬而远之。下面介绍一种求三角函数有理式不定积分的比较简单的方法——关联辅助积分法。

以上方法是用换元法,把被积的三角函数有理式先转化为代数有理式,再求该代数有理式的积分。但我们看到这个转化的过程往往相当繁琐,转化后的代数有理式函数的积分,也比较难求(以上例题一般用待定系数法把被积的三角函数有理式拆分成三个容易积分项的积分),有的甚至无法求出,下面介绍一种较为巧妙而简单的积分方法——关联辅助积分法。
解法二:用关联辅助积分法
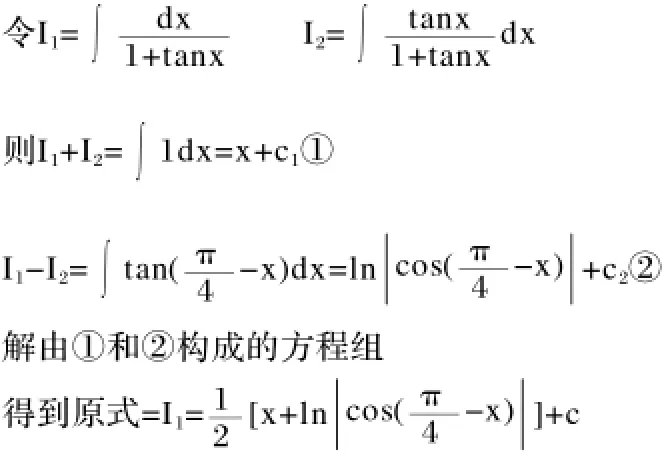
用这种积分法则容易多了
不过用这种方法要注意的是,在找关联辅助积分时,一定要本着原积分与辅助积分所构成的线性组合积分比原积分要容易求为原则。[1]
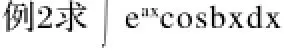
解法一:用分部积分法,此题一般就是用分部积分法,要两次运用分部积分法,然后出现循环现象,通过解方程间接得出结果。
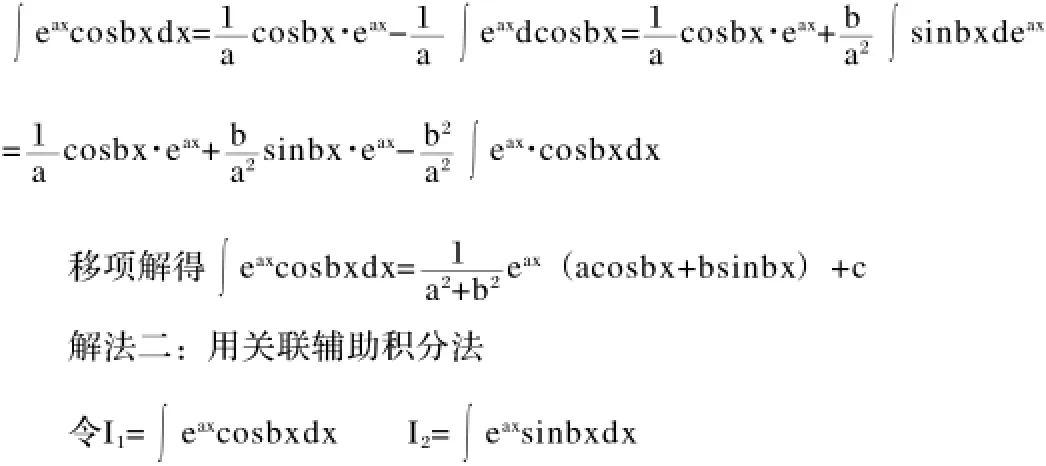

以上关联辅助积分法是将求积分的问题化为解线性方程组的问题,简捷、容易!如果被积函数比较复杂,则更能体现出用关联辅助积分法的优越性。[2]

该形式的积分正类似于吉米多维奇著《数学分析习题集》第2042题所述公式,但该公式难记,学生一般记不住。解题时不用记如此复杂的公式,用以上关联辅助积分法可即时求解。


同时也可求I1和I2。
关联辅助积分法就是找出与所求不定积分相关联的一个(或两个)不定积分,再构造所求不定积分与这一个(或两个)不定积分的两个(或三个)线性组合积分,因为这两个(或三个)线性组合后的积分容易求出,所以最后通过解二元(或三元)一次方程组就可求出原积分和其相关联的这一个(或两个)辅助积分。
[1]李艳萍.一类三角函数的辅助积分法[J].北京电力高等专科学校学报,2009年4月:152-153
[2]万丽, 王剑侠.一种含三角函数式积分的特殊方法[J].高等数学研究,2000,3卷(4期):23-24
邓敏(1967—),女,副教授,硕士研究生,研究方向:高等数学、数学课程论的教学与研究。

