新型架空直立式码头结构动力响应分析
孙兴毅, 张淑华, 张文敬, 刘春阳, 陈光明
(河海大学港口海岸与近海工程学院,江苏南京210098)
架空直立式码头结构是为了适应我国西部内河高水位落差而修建的一种码头结构型式,具有装卸效率高、通过能力大等优点,目前已成功运用于长江中下游地区。由于架空直立式码头结构是针对我国特定的水文环境提出来的结构,国外缺乏类似的河流条件,所以相应的研究都集中在国内,国外几乎未见到相应研究。架空直立式码头结构与传统的高桩码头结构相比,增加了横撑和纵撑的作用,再加上受到船舶撞击、堆货荷载以及岸吊等竖向荷载作用,使得其受力非常复杂。
黄建勇[1]等利用有限元方法对内河架空直立式码头进行计算分析,建立了3种不同的有限元模型,分别进行静力计算和比较分析,结果表明考虑面板刚度的空间刚架模型是适合内河大水位差架空直立式码头结构的计算模型。王多垠[2]等采用单位力法对内河架空直立式码头结构二维平面模型可能出现的荷载工况进行了有限元计算,得到计算结构各主要构件控制内力的最不利作用效应组合,提出内河架空直立式集装箱码头结构计算的作用效应组合方法。刘明维[3]等基于单位力方法,计算得到内河架空直立式码头三维结构模型在多种工况条件下各主要受力构件的内力,得到前排桩在低水位船舶荷载下出现最不利内力情况,其它构建在高水位船舶荷载作用下较容易出现最不利状态;高水位的系缆力对横梁弯矩起主导可变作用,轨道梁横梁以承受弯矩为主,立柱前后排桩基以承受轴力为主。吴飞桥[4]等利用有限元软件ANSYS对架空直立式码头结构在水平地震作用下的受力进行数值分析,得出码头结构基频由于大量纵向联系梁的存在而提升,有利于结构抗震;码头主要构件的剪力和弯矩最大值发生在结构的最底层,并沿高度逐层递减,水平位移分布随着激励方向的改变而不同,横向激励下只产生横向位移,纵向激励下纵横向都产生位移。戴俊[5]等基于结构受力最优及工程造价最省的原理提出空间三角形框架墩加带主斜撑大跨度排架新型架空直立式码头,并与寸滩码头进行对比,表明新型码头结构具有构造简单、受力合理、水下工程量小等优点。
随着长江三峡库区水位的提高,长江上游地区河床地质发生了很大改变,诱发地震的可能性也相应提高[6-7],考虑在今后实际中的应用,利用有限元分析软件ABAQUS建立了传统架空直立式码头和新型码头结构的有限元模型进行动力响应分析,研究对比两种码头结构的面板位移、桩位移及桩弯矩等要素,为以后该新型码头结构的运用提供参考。
1 码头结构有限元模型建立
传统架空直立式码头结构和新型架空直立式码头结构断面如图1所示。分别选取传统码头结构和新型码头结构的一段四跨五榀排架建立有限元模型,为更好地分析两种码头结构桩的动力响应,对码头结构进行编号;两种结构均包含5个截面(1#~5#),每个截面上桩的号码为该截面的截面号和该截面上桩所在位置从左到右(正视方位)序号的组合,即传统码头1#截面从左向右桩号分别为11#,12#,13#,14#,15#,其它截面依次类推。码头结构混凝土材料为C30,弹性模量为3e7Pa,泊松比为1/6,密度为2 500 kg/m。分析时将码头结构作为线弹性体考虑,建立有限元模型如图2所示。

图1 码头结构断面Fig.1 Wharf structure section

图2 有限元模型Fig.2 Finite element model
2 模态分析
振动模态是弹性结构固有的、整体的特性。结构的每一个模态具有特定的固有频率、阻尼比和模态振型。这些模态参数可以由计算或试验分析取得,这样一个计算或试验分析过程称为模态分析。模态分析方法在结构动力学中是以无阻尼的各阶主振型所对应的模态坐标代替物理坐标,使微分方程解耦,变成各个独立的微分方程。一个N自由度线形系统的运动微分方程可表示为
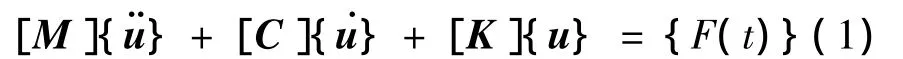
式中:[M]为结构质量矩阵;[C]为结构阻尼矩阵;[K]为结构刚度矩阵;{u}为节点位移向量;{}为节点速度向量;{}为节点加速度向量;[F(t)]为节点荷载向量。
模态分析是对无外荷载作用下的结构进行求解其自由振动结果的计算分析,并且在模态分析中,结构的阻尼对其自振特性影响均较小。故可以把不考虑阻尼和外荷载作用的结构振动微分方程改为
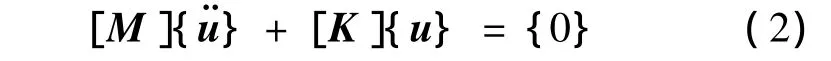
在模态分析中,将结构的自由振动形式视为简谐振动。此时,其节点位移向量和节点加速度向量的表达式为
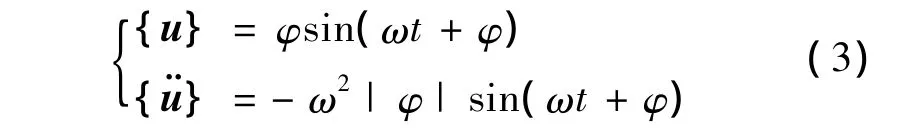
将式(3)带入式(2)得到结构振动的特征方程:

模态分析就是计算方程(4)中的特征值ω1(即结构的固率)和其对应的特征向量|φi|。
利用有限元软件ABAQUS提取两种码头结构的前4阶模态,各自自振频率和最大振幅如表1所示。

表1 两种码头前4阶模态分析结果Fig.1 Two pier and the modal analysis results
从固有频率分析,传统码头在前3阶固有频率(基频)在0.9~1.1区间内且变化不大,表明传统码头结构在各个方向的整体刚度较为均匀;新型码头的自振频率在不同阶段变化明显,平均每阶模态之间自振频率大小的变化在1 Hz左右。这说明新型码头在不同方向的刚度欠均匀,即受到某个方向激励时产生的响应大于受到其余方向激励时的响应。
虽然相对于传统码头而言,新型码头各阶模态时均有较大的自振频率,新型码头第1,3,4阶模态最大振幅均小于传统码头,另外新型码头结构在第1,3,4阶模态时新型码头的运动趋势主要是沿水平方向,因而可以初步推断新型码头在垂岸方向刚度较大。
3 动力响应分析
研究中选用10 s持时的EI-Centro波作为输入地震波,由于架空直立式码头所处的重庆地区抗震设防烈度为6度,设计基本地震加速度峰值为0.05 g。文中对所选取地震波进行调整,采用的地震波调幅系数为0.15,即实际波形为调幅波形后的0.15倍,调整后波形如图3所示。

图3 调整后振型Fig.3 Mode after adjusting
利用基于ABAQUS二次开发的边界面模型,对有限元模型进行动力响应分析[8-9],模型参数M=1,G=8 000 kPa,V=0.3,η =100,β =3,κ =0.034,γ=0.17。提取两种码头结构面板的水平位移响应时程如图4所示。从面板的水平位移时程图来看,传统码头面板水平位移响应值处于-3.5~3.6 cm之间,而新型码头的面板水平位移响应值处于-5.488~4.176 mm之间,后者区间范围小于前者。从振动频率来看,新型码头振动时面板水平位移的波峰和波谷间周期短、频率高,而传统码头振动时面板水平位移的波峰和波谷间频率相对于新型码头较低。由模态分析知道,新型码头刚度较大,因此可以判断地震作用时新型码头容易发生局部断裂损伤破坏,而传统码头则容易发生整体塌陷破坏。

图4 码头结构面板水平位移响应Fig.4 Wharfstructure panelhorizontal displacement response
提取两种码头结构各截面桩水平位移峰值响应如图5所示。从两种码头桩身的水平位移峰值响应来看,传统码头各截面上典型桩位移峰值均随着桩身高度的增加而增大。由于土体的约束作用,在土中桩段位移峰值随桩高的增大趋势明显要小于出土桩段位移峰值随桩高的增大趋势。同时,由于埋置深度不同,各截面上典型桩在土中桩段位移峰值随桩高增大趋势也不相同。新型码头各截面上典型桩的位移峰值同样随着桩身高度的增加而增大,与传统码头不同的是新型码头各截面典型桩位移峰值从桩底端到与斜撑交界截面位置变化很小,之后位移峰值逐渐增大。可以看出,斜桩对新型码头整体具有较好的支承作用。同时,斜桩水平位移峰值变化曲线较为复杂,这主要是由于斜桩各跨长度变化较大所致。
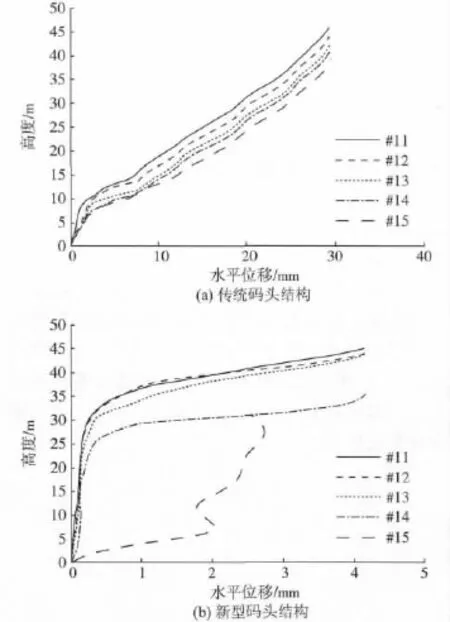
图5 码头各截面桩最大水平位移响应Fig.5 Maximum horizontal displacement response of each section pile
提取两种码头结构各截面桩最大加速度响应如图6所示。从桩身水平加速度峰值响应来看,两种码头各截面典型桩水平加速度峰值均呈现先减小后增大的趋势。最小值出现在靠近桩身和土体表面交界处,最大值出现在桩身顶部。除新型码头斜桩截面上典型桩外,两种码头各截面典型桩的水平加速度最大值和最小值差别不大,但最小值出现的位置同样与桩的入土深度相关,即桩在土体中部分越长桩身加速度峰值出现的位置距桩底端距离越大。对于新型码头斜桩截面典型桩,除0~7 m这段初始部分以外,其加速度随桩高整体的变化趋势与其他截面的典型桩类似。

图6 码头各截面桩最大加速度响应Fig.6 Maximum acceleration response of each section pile
提取两种码头结构第1排架近岸桩弯矩峰值响应如图7所示。从桩身弯矩峰值响应来看,两种码头典型桩第1个拐点均出现在桩与土体表面交界位置附近,传统码头典型桩弯矩峰值最大值分别出现在第1个拐点以及靠近桩顶端处,峰值最小值出现在桩顶端。新型码头典型桩在斜撑顶端水平面附近出现了两处弯矩峰值最小值,峰值最大值同样出现在桩顶端。整体来看,新型码头在斜撑顶端水平面以下桩身各段弯矩峰值最大、最小值绝对值均较小,且变化幅度不大,但在该平面以上桩身各段弯矩峰值最大、最小值绝对值大小出现了较大变化,但其峰值均小于传统码头的峰值。

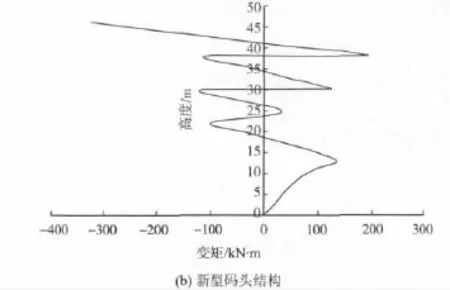
图7 码头结构近岸直桩弯矩峰值响应Fig.7 Bendingmomentpeak responseofwharf structure of the nearshore straight pile
4 结语
1)通过提取两种码头结构振动模态,可以看出新型码头由于受到斜撑的影响,相对传统结构刚度的各向不均匀性有所增加,但是码头结构的刚度有所增加,尤其是垂岸方向,使得振动幅值相比传统结构有所减小。
2)通过对比分析,可以看出新型码头结构面板水平位移明显减小。新型码头截面上桩的位移峰值变化同传统码头结构一样,随着桩身高度的增加而增大,不同的是新型码头各截面典型桩位移峰值从桩底端到与斜撑交界截面位置变化很小,之后位移峰值才逐渐增大。
3)由于受到斜撑的作用,码头与斜撑连接面以下桩的弯矩变化较小,连接面以上弯矩变化比较大,但是变化峰值依然小于传统码头结构。但是值得注意的是,这种变化的不均匀容易引起码头结构的局部破坏,在以后的设计施工中应引起足够的重视。
[1]黄建勇,王多垠.内河架空直立式集装箱码头结构计算模型探讨[J].水道港口,2008,29(1):59-62.
HUANG Jianyong,WANG Duoyin.Inland overhead vertical structure calculating model of container terminal[J].Channel Port,2008,29(1):59-62.(in Chinese)
[2]王多垠,石兴勇,丁德斌,等.内河架空直立式集装箱码头结构计算中的作用效应组合探讨[J].中国港湾建设,2005(4):33-35.
WANG Duoyin,SHI Xingyong,DING Debin,et al.Inland overhead upright container wharf structure calculation of effect combination study[J].Journal of China Harbor Construction,2005(4):33-35.(in Chinese)
[3]刘明维,舒丹,吴林键,等.基于单位力法的内河架空直立式码头三维空间结构计算中作用效应组合分析[J].水运工程,2014(10):47-52.
LIU Mingwei,SHU Dan,WU Linjian,et al.Based on unit force method of inland water overhead vertical wharf in three dimensional space structure calculation effect portfolio analysis[J].Port and Waterway Engineering,2014(10):47-52.(in Chinese)
[4]吴飞桥.地震荷载作用下内河架空直立式集装箱码头数值分析[D].重庆:重庆交通大学,2010.
[5]戴俊,杨波,袁赵龙,等.内河架空直立式码头新型优化结构型式研究[J].重庆交通大学学报:自然科学版,2013,32(4):1674-0696.
DAI Jun,YANG Bo,YUAN Zhaolong,et al.Inland elevated vertical wharf new optimized structure study[J].Journal of Chongqing Jiaotong University:Natural Science Edition,2013,32(4):1674-0696.(in Chinese)
[6]陈蜀俊,苏爱军,罗登贵.长江三峡水库诱发地震的成因类型[J].大地测量与地球动力学,2004,24(2):70-73.
CHEN Shujun,SU Aijun,LUO Denggui.The genetic type of the Yangzi river three gorges reservoir induced earthquake[J].Journal of Geodesyand Geodynamics,2004,24(2):70-73.(in Chinese)
[7]陈德基.三峡工程水库诱发地震问题研究[J].岩石力学与工程学报,2008,9(8):1513-1524.
CHEN Deji.Study of the problem of three gorges reservoir induced earthquake[J].Journal of Rock Mechanics and Engineering,2008,9(8):1513-1524.(in Chinese)
[8]刘晶波,杜义欣,闫秋实.黏弹性人工边界及地震动输入在通用有限元软件中的实现[C]//中国土木工程学会,南京工业大学.第三届全国防震减灾工程学术研讨会论文集,南京:中国土木工程学会,南京工业大学,2007.
[9]费康,张建伟.ABAQUS在岩土工程中的应用[M].北京:中国水利水电出版社,2010.

