基于改进的Theil不等系数及IGOWC-OWHA算子的区间型组合预测模型
张 超, 袁宏俊
(安徽财经大学统计与应用数学学院,安徽蚌埠233030)
受Bates与Granger上世纪60年代第一次系统性的探究组合预测方法[1]的影响,组合预测方法的应用得到众多相关学者的青睐,并取得了丰硕的研究成果[1-6]。但是大部分组合预测的方法都是局限于单点序列的预测,而在区间数组合预测方面较为少见。然而从实际考虑,很多数据通常以区间数的形式表现出来会显得更为合理,因此将这些区间数进行组合预测具有重要的研究意义和价值。
关于区间数的组合预测研究是一个庞大的课题,不同研究者存在不同的研究角度。文献[7-9]的方法只局限于离散区间数据的组合预测,而对于连续区间数据的预测并不适用,因此Yager于2004年通过一个态度参数将区间值集结成一个实数,构造出连续区间数有序加权平均(C-OWA)算子[10];文献[11]把 C-OWA算子拓展为 WC-OWA算子、OWC-OWA算子以及CC-OWA算子;文献[12]综合C-OWA算子与OWGA算子构造连续区间有序加权几何平均(C-OWGA)算子;文献[13]提供了连续区间数广义有序加权平均(C-GOWA)算子;文献[14]结合 IOWA算子与 C-GOWA算子构造出IOWC-GOWA算子;文献[15]综合IOWA算子和C-OWA算子,构造出一种诱导连续区间有序加权平均(IC-OWA)算子;文献[16]综合C-OWA算子与OWHA算子构造出连续区间有序加权调和平均(C-OWHA)算子,并在此基础上提出了加权调和的C-OWHA(WHC-OWHA)算子、有序加权调和的C-OWHA(OWHC-OWHA)算子和组合的C-OWHA(CC-OWHA)算子。
受上述研究成果启发,文中将IGOWA算子与C-OWHA算子加以综合,构造出一种诱导广义有序加权的C-OWHA(IGOWC-OWHA)算子,并研究其部分性质。选取改进的Theil不等系数作为相关性指标,建立新型组合预测模型,最后通过算例分析证实该方法在提高预测精度方面具有显著效果。
1 基本定义
定义1[4]假设fw:Rn→R为n元函数,倘若
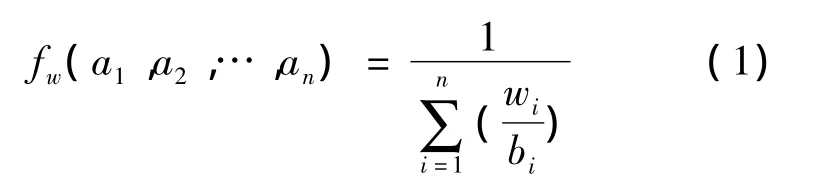
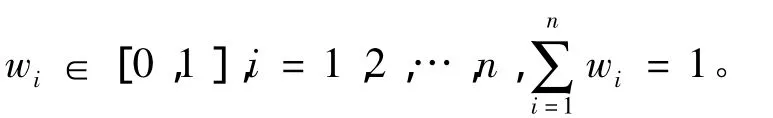
定义2[16]设[a,b]为区间数,称
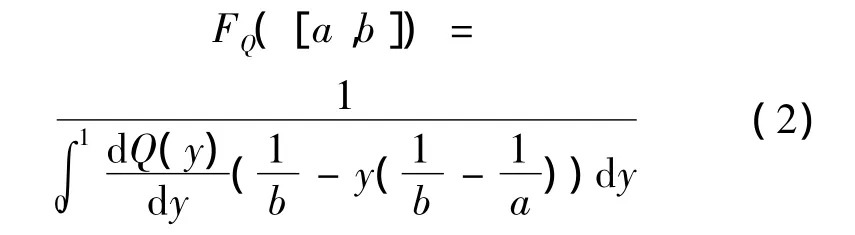
为连续区间数有序加权调和平均(C-OWHA)算子,其中Q(y):[0,1]→[0,1]为基本的单位区间单调(BUM)函数且满足:Q(0)=0;Q(1)=1;当y1>y2时,有Q(y1)≥Q(y2)。
定义3[16]给定基本单位区间单调(BUM)函数Q(y),记

的态度参数。
由定义3及式(2)可得

定义4[6]假设〈v1,a1〉,〈v2,a2〉,…,〈vn,an〉为 n个二维数组,令
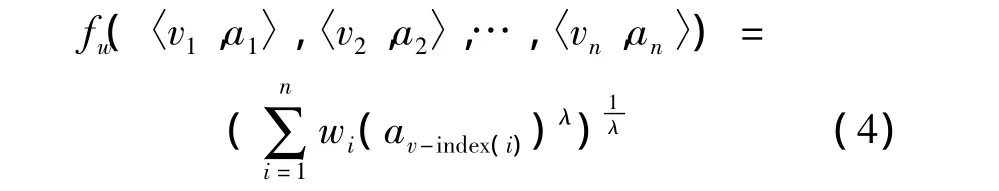

2 IGOWC-OWHA算子及其性质
尽管C-OWHA可以集结连续的区间数,可是C-OWHA算子仅局限于解决单一区间数据的集结问题,如果想要集结更多区间数据的信息,还需对C-OWHA算子予以扩展。
定义5 假定[ai,bi]是一组区间数,〈v1,[a1,b1]〉,〈v2,[a2,b2]〉,…,〈vn,[an,bn]〉是二维数组,设 g:Ω+→ R+,若

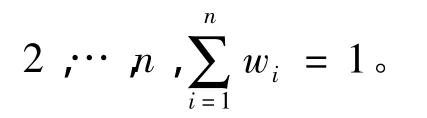
IGOWC-OWHA算子的特点在于:首先运用定义2中的C-OWHA算子集结每个区间[ai,bi]的全部数据,再将集结后的全部数据运用定义4的IGOWA算子集结。根据定义5不难证明以下性质[16]。由于篇幅有限,文章仅给出单调性证明过程。
定理1(单调性)对于任意的 i=1,…,n,若有ai≥a'i,bi≥ b'i则
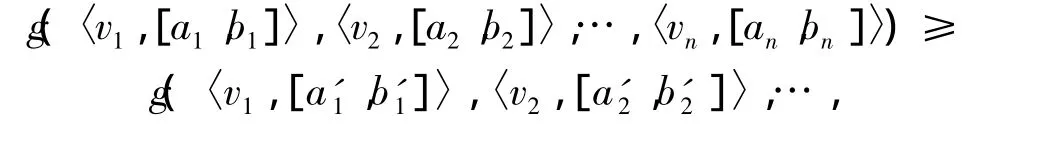
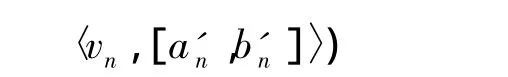
证将式(5)两侧取以ex为底的对数,得
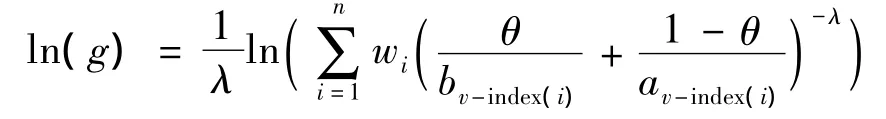
两侧对av-index(i)分别求导得
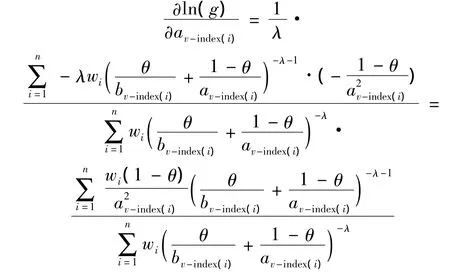
在上式中,由于
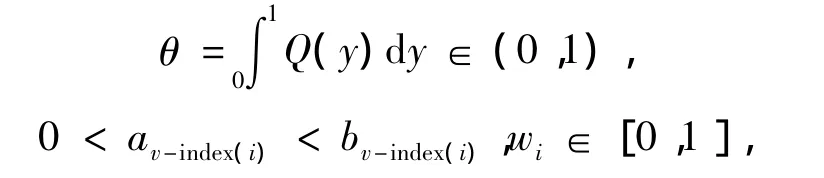
则
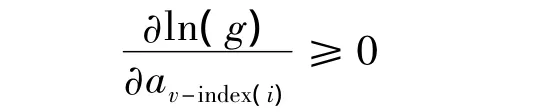
所以函数g关于av-index(i)单调递增。同理可得,函数g亦关于bv-index(i)单调递增。
由命题假设可知,ai≥ a'i,bi≥ b'i,得
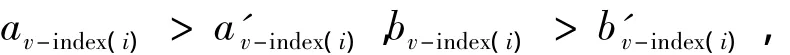
又函数g均关于av-index(i)和bv-index(i)单调递增,故
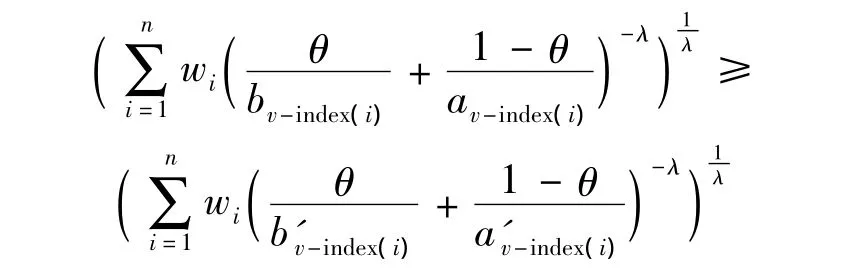
即

所以命题得证。
定理2(幂等性)对于任意的 i=1,…,n,若有[ai,bi] = [a,b],则
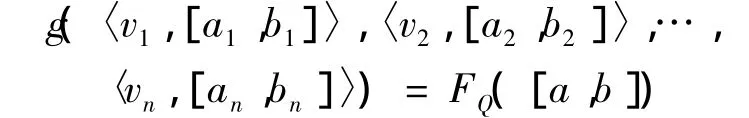
定理3(介值性)若[ai,bi](i=1,2,…,n)是任一区间数组,且0<ai<bi,则存在
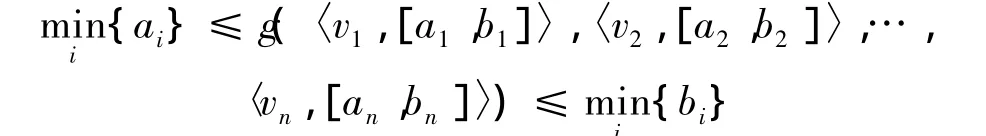
定理4(置换不变性)设 π =(π(1),π(2),…,π(n))是(1,…,n)的任一置换,得到
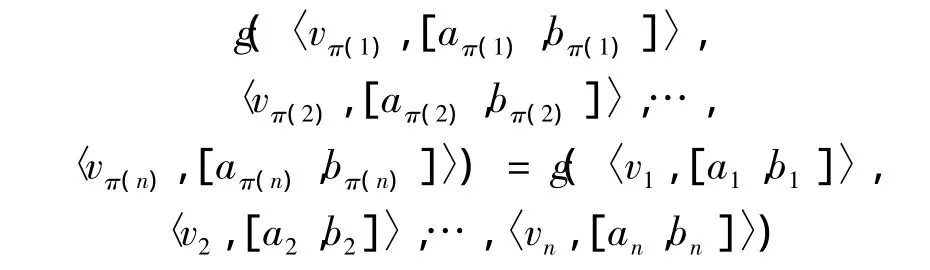
3 基于改进的Theil不等系数的IGOWC-OWHA算子的区间组合预测模型
设某一区间时序的观测值为xt=[at,bi](t=1,2,…,N),同时 xt也可等价表示成 xi= [ct,ri](t=1,2,…,N),其中

分别记作区间数xt的中心与半径,假定用于预测的单项方法有m种,且它们都应用到组合预测当中,设第i种方法在第t时点的单项预测值为=,),同样也可以等价成=),i=1,2,…,m,t=1,2,…,N。wi是第 i种单项方法在组合预测中的权重
定义6 令
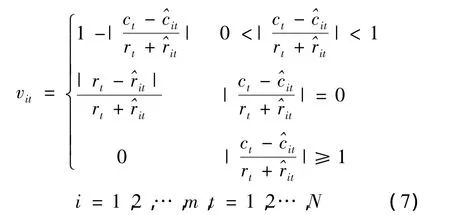
则称vit为第i单项方法在第t时点的预测精度,vit∈[0,1]。将 vit当做预测值()的诱导变量,由此可以根据每一个vit以及与之相对应的构建m个二维数组,即〈vmt,[]〉。根据定义3 以及定义5 可推出如下几个算式:令
其中,yt为实际区间值由C-OWHA算子生成的时刻实际集结值是由C-OWHA算子生成的各个单项方法各个时刻预测值的单项预测集成值为由IGOWC-OWHA算子生成的t时刻组合预测集成值;W=(w1,w2,…,wm)T是 m种单项方法在组合预测中的权向量,满足,显然 wi≥ 0,i=1,2,…,m;v-index(i)是 v1,v2,…,vn遵循由大到小的原则排列后序号为i的数的下标。
Theil不等系数常常被用来评价预测效率的优劣,为此文中将其作为相关性指标,对区间组合预测效率予以评价。
定义7[3]令
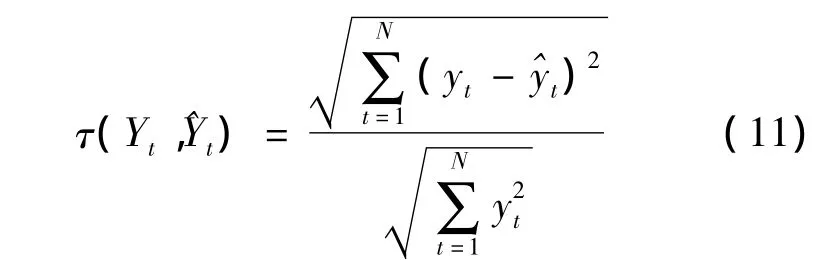
将 τ(Yt,)称作实际值 yt(t=1,2,…,N)与组合预测值(t=1,2,…,N)间改进的Theil不等系数,τ(Yt)∈[0,∞)。τ(Yt)越低表明预测效率越高。
当实际值yt(t=1,2,…,N)等于组合预测值^yt(t=1,2,…,N)时,它们相应的 τ(Yt,)值将会是最低值,即τ(Yt)=0。又因为τ(Yt)是所有单项方法权重w1,w2,…,wm的函数,所以可表示成τ(w1,w2,…,wm)。故基于改进的 Theil不等系数及IGOWC-OWHA算子的最优组合预测模型如下所示:

该模型可借助LINGO软件进行求解。
4 实例分析
出于检验IGOWC-OWHA算子的区间型组合预测模型是否有效的目标,文中直接采用文献[7]的数据作为参考资料。但是文献[7]只给出3种单项预测方法的预测数据,并没有对这3种单一方法性质进行比较。所以,基于区间组合预测研究领域的局限性,文中无法给出3种单一方法性质的比较,将重点讨论区间组合预测模型与3种单一模型预测精度的比较。
表1列出了区间实际数据和单项方法预测数据。

表1 区间实际数据和单项方法预测数据Tab.1 Interval actual data and individual method forecast data
依据式(7)计算得到各个单项方法在各个时间点的预测精度数据,如表2所示。

表2 预测精度数据Tab.2 Prediction accuracy of the data
由式(8)可以计算出实际区间值由C-OWHA算子所生成的t时刻实际集成值yt。由于yt中的态度参数θ由BUM函数Q(y)决定,所以为了便于比较,文中分别取Q1(y)=y2;Q2(y)=y3。则

表3给出由上述两个态度参数计算得到的实际区间集成值。

表3 实际区间集成数据Tab.3 Integrated data of the actual interval
根据表2中的诱导变量及式(10)计算IGOWC-OWHA算子生成的组合预测集成值^yt,为了便于比较,分别取λ1=1,λ2=2,λ3=3,λ4=4,λ5=5这5个参数进行讨论。共有10种情况,依次予以计算。
1)当θ=1/3时,以λ=2为例,计算过程如下:
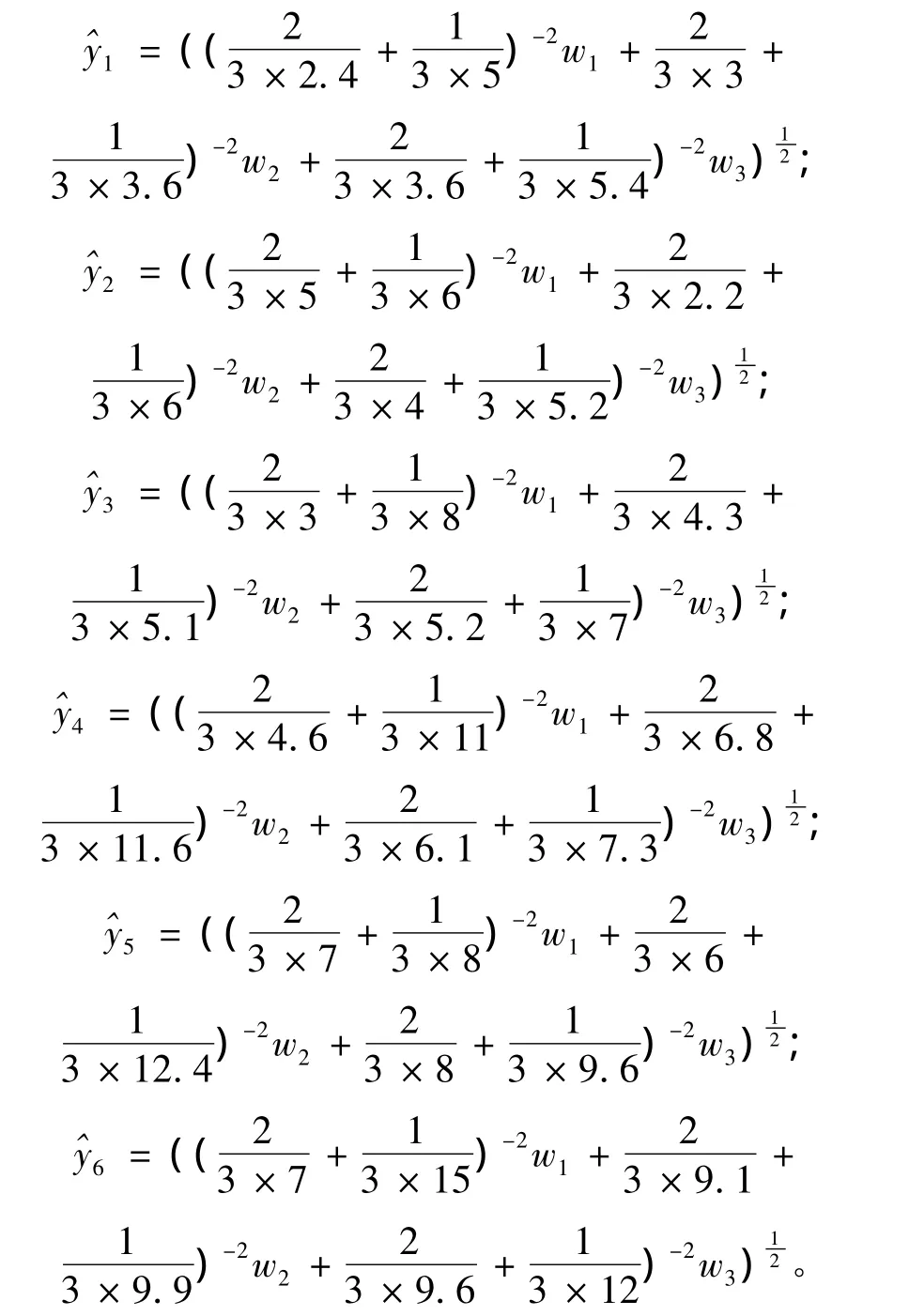
将上述表达式与表3中的θ1=1/3时的实际区间数集成值代入到单目标最优模型式(12)中,再运用Lingo15软件解得最优权重向量为

除此之外,当λ取1,3,4,5时,对应的最优权重向量分别为

2)当θ=1/4时,以λ=3为例,计算过程如下:
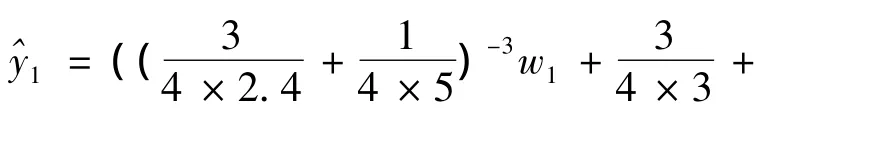
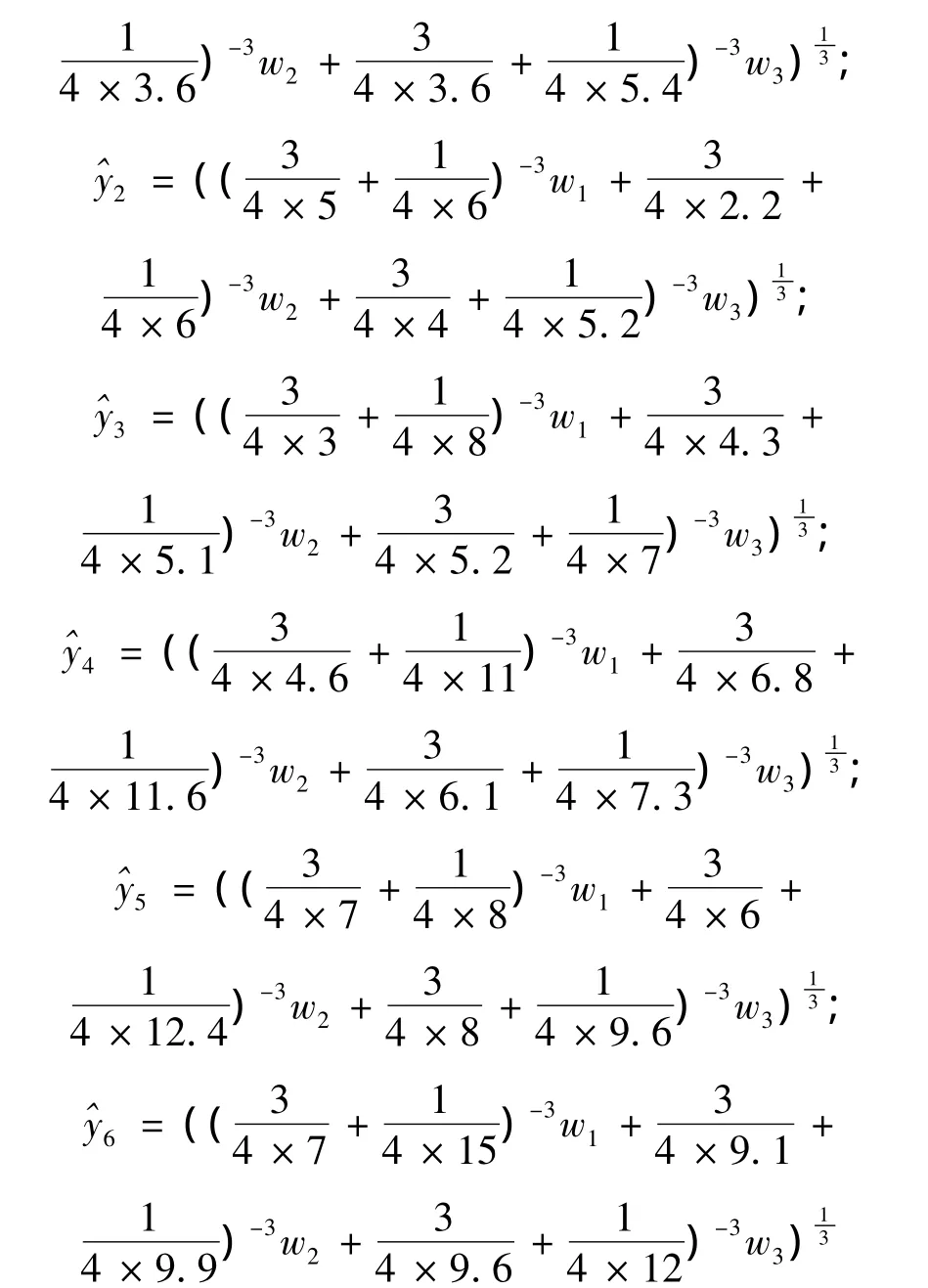
将上述表达式与表3中的θ2=1/4时的实际区间数集成值代入到单目标最优模型式(12)中,再运用Lingo15软件解得最优权重向量为
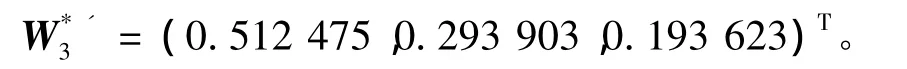
除此之外,当λ取1,2,4,5时,对应的最优权重向量分别为

为了证明区间组合预测模型是否有效,可选取MSEP,MSEL,MSEI,MRIE 作为评价准则:
1)平均区间位置误差平方和
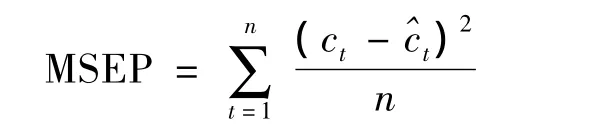
2)平均区间长度误差平方和
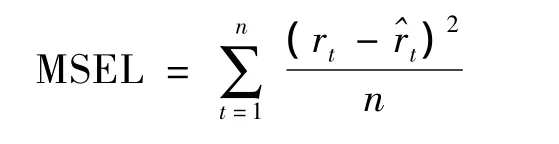
3)平均区间误差平方和
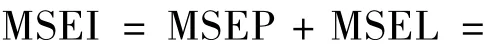
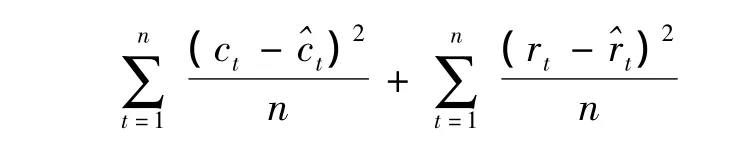
4)平均相对区间误差和

表4给出相应的分析结果。
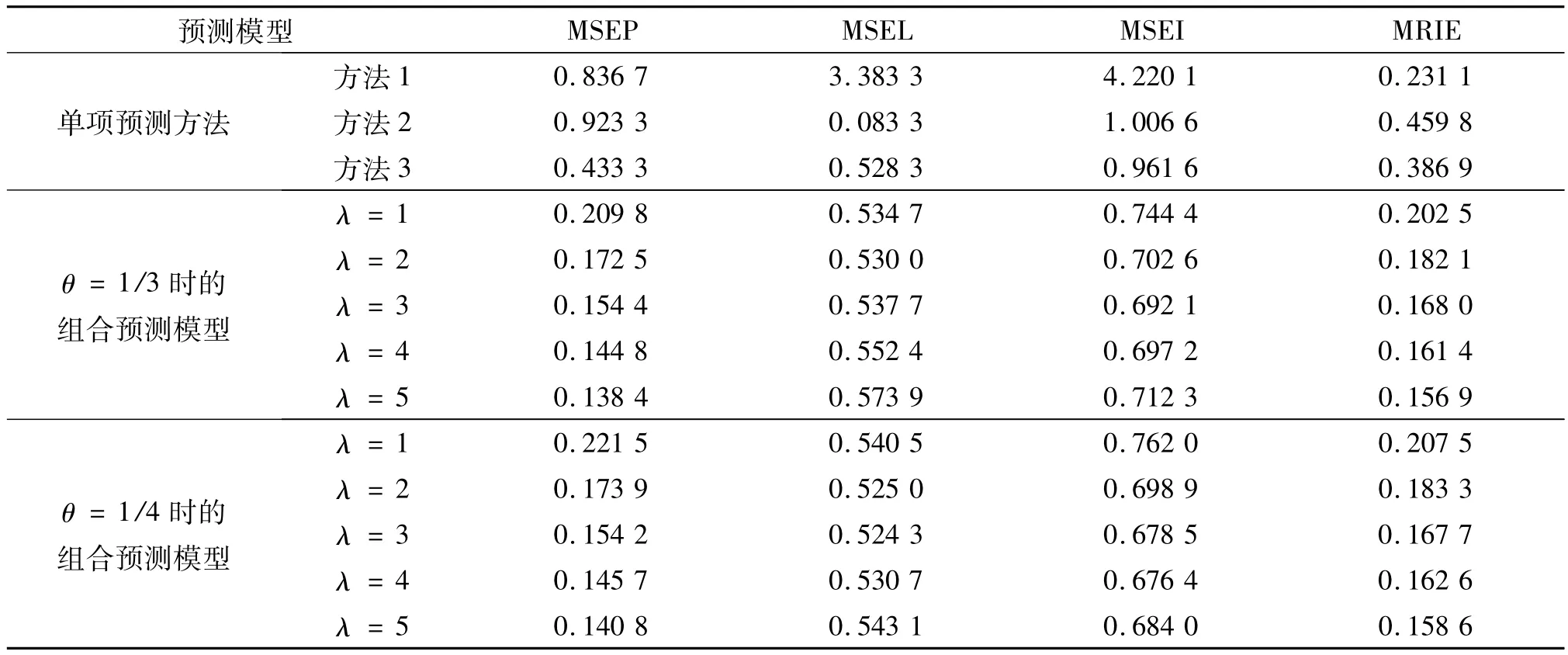
表4 误差指标Tab.4 Error indicators
观察表4易知,基于 Theil不等系数及IGOWC-OWHA算子的区间型组合预测模型的MSEP,MSEI,MRIE都显著小于各单项方法误差指标值,虽然MSEL指标不够显著,但并不是最大的,因此该区间组合预测新方法至少是非劣性的。综合来看,基于Theil不等系数及IGOWC-OWHA算子的区间型组合预测模型可以显著提高预测精确度。
5 结语
大多数组合预测方法仅局限于离散区间数据的组合预测,但对于连续区间数据的组合预测较为少见。对连续区间数组合预测是一个全新的研究方向,文中提出一种更加有效的方法。文中引入IGOWA算子与C-OWHA算子结合,构造出诱导广义有序加权的C-OWHA(IGOWC-OWHA)新型算子。由于该算子可以集结多个区间数据的信息,所以可以将其应用于连续区间数的组合预测中。利用IGOWC-OWHA算子,再结合改进的Theil不等系数作为相关性指标,构建区间型组合预测新模型,并经过算例验证了其有效性,揭示出该方法在提高预测精度方面具有显著效果。但是,文中考虑的θ和λ情况有限,是否存在某个θ值和λ值使预测效果更加精确还需要通过进一步研究。
[1]Bates J M,Granger C W J.The combination of forecasts[J].Operational Research Society,1969,20(4):451-468.
[2]王应明.基于相关性的组合预测方法研究[J].预测,2002,21(2):58-62.
WANG Yingming.Research on the methods of combining forecasts based on correlativity[J].Forecasting,2002,21(2):58-62.(in Chinese)
[3]陈华友.基于Theil不等系数的组合预测模型的性质[J].电子科技大学学报,2004,33(1):105-108.
CHEN Huayou.Properties of combination forecasting models based on theil coefficient[J].Journal of UEST of China,2004,33(1):105-108.(in Chinese)
[4]陈华友,刘春林,盛昭瀚.IOWHA算子及其在组合预测中的应用[J].中国管理科学,2004,12(5):35-40.
CHEN Huayou,LIU Chunlin,SHENG Zhaohan.Induced ordered weighted harmonic averaging(IOWHA)operator and its application to combination forecasting method[J].Chinese Journal of Management Science,2004,12(5):35-40.(in Chinese)
[5]袁宏俊,陈华友,胡凌云.基于指数支撑度的最优组合预测模型及其性质研究[J].应用概率统计,2012,28(2):150-160.
YUAN Hongjun,CHEN Huayou,HU Lingyun.Research on the optimal combination forecating model and its properties based on exponential supporting degree[J].Chinese Journal of Applied Probability and Statistics,2012,28(2):150-160.(in Chinese)
[6]杨蕾,陈华友,王宇.基于贴近度的诱导广义OWA算子最优组合预测模型[J].统计与决策,2013,377(5):24-26.
YANG Lei,CHEN Huayou,WANG Yu.The optimal combination forecating model based on closeness degree and induced generalized ordered weighted averaging(OWA)operator[J].Statistics and Decision,2013,377(5):24-26.(in Chinese)
[7]徐惠利,吴柏林,江韶珊.区间时间序列预测精准度探讨[J].数量经济技术经济研究,2008,25(1):133-140.
XU Huili,WU Bolin,JIANG Shaoshan.On forecasting efficiency evaluation for interval time series[J].The Journal of Quantitative and Technical Economics,2008,25(1):133-140.(in Chinese)
[8]陈华友,李翔,金磊,等.基于相关系数及IOWA算子的区间组合预测方法[J].统计与决策,2012,354(6):83-86.
CHEN Huayou,LI Xiang,JIN Lei,et al.The methods of interval combination forecasting based on the correlation coefficient and induced ordered weighted averaging(IOWA)operator[J].Statistics and Decision,2012,354(6):83-86.(in Chinese)
[9]胡凌云,袁宏俊.基于左右端点的IOWGA算子的区间型组合预测模型[J].统计与决策,2013,383(11):22-25.
HU Lingyun,YUAN Hongjun.The inlerval combination forecasting model based on the left-right endpoint and induced ordered weighted geometric averaging(IOWGA)operator[J].Statistics and Decision,2013,383(11):22-25.(in Chinese)
[10]Yager R R.OWA aggregation over a continuous interval argument with applications to decision making[J].IEEE Transactions on Systems,Man,and Cybernetics,Part B,2004,34(5):1952-1963.
[11]徐泽水.拓展的C-OWA算子及其在不确定多属性决策中的应用[J].系统工程理论与实践,2005,25(11):7-13.
XU Zeshui.Extended C-OWA operators and their use in uncertain multi-attribute decision making[J].Systems Engineering-Theory and Practice,2005,25(11):7-13.(in Chinese)
[12]Yager R R,XU Z S.The continuous ordered weighted geometric operatorand its application to decision making[J].Fuzzy Sets and Systems,2006,157(10):1393-1402.
[13]Yager R R.Generalized OWA aggregation operators[J].Fuzzy Optimization and Decision Making ,2004,3(1):93-107.
[14]江立辉,陈华友,丁芳清,等.基于IOWC-GOWA算子的区间组合预测模型[J].计算机工程与应用,2015,51(3):50-54.
JIANG Lihui,CHEN Huayou,DING Fangqing,et al.Combination forecasting model based on induced ordered weighted continuous generalized ordered weighted averaging operator[J].Computer Engineering and Applications,2015,51(3):50-54.(in Chinese)
[15]周礼刚,陈华友,王晓,等.诱导连续区间有序加权平均算子及其在区间数群决策中的应用[J].控制与决策,2010,25(2):179-184.
ZHOU Ligang,CHEN Huayou,WANG Xiao,et al.Induced continuous ordered weighted averaging operators and their applications ininterval group decision making[J].Control and Decision,2010,25(2):179-184.(in Chinese)
[16]陈华友,刘金培,王慧.一类连续区间数据的有序加权调和(C-OWH)平均算子及其应用[J].系统工程理论与实践,2008,28(7):86-12.
CHEN Huayou,LIU Jinpei,WANG Hui.A class of continuous ordered weighted harmonic(C-O W H)averaging operators for interval argument and its applications[J].Systems Engineering-Theory and Practice,2008,28(7):86-12.(in Chinese)

