多因素约束韦伯型设施的选址问题
李 磊, 陈文斌
(江南大学商学院,江苏 无锡214122)
随着经济社会的发展,设施选址问题日益成为运筹学和计算应用领域的研究核心。设施选址问题的主要思想是在客户、资源、目的等条件已知的情况下,确定一个或者多个新设施点,最大化使用资源[1]。通常需要数学、管理学、计算机、金融学等多学科知识的融合来建立模型,解决问题,其研究理论日渐成熟和完善。
选址问题是一个古老又经典的问题,早在1634年,法国数学家Fermat提出了在一个平面上有任意3点,试求第4点,使之到这3个点构成的距离最短。该问题在17世纪由意大利数学家托里切利解决,这个点被称为“费马点”。1750年,辛普森(T.Simpson)提出了一种加权情形:若 A1,A2,A3,为平面上给定的3个点,又wi> 0(i=1,2,3),求平面上一点A0,使∑wi‖A1A0‖|最小。19世纪初,瑞士几何学家Steiner将此问题推广到n个点:求平面上一点至已给n个点的距离之和最小,此问题称为斯坦纳问题[2]。1909年德国经济学家韦伯以斯坦纳问题为理论模型,首先提出了设施选址问题,其研究对象为在工业区内建立一个仓库使得到不同需求方的总距离最小[3]。
近年来,伴随着计算机技术的发展,智能算法在设施选址问题上做出了巨大贡献。Harry Venables和Alfredo Moscardini提出搜索启发性算法,采用蚁群优化(ACO)进行设备随机选择,得到CFCLP问题的近似最优解[4]。Lyamine Bouhafs等人采用模拟退火算法和蚁群算法解决选址行程问题(LRP)。Blas Pelegrín等人设计了一个改进的遗传算法,在位置集合m中选择一系列的厂址,以满足假定条件下的最优。对于算法的有效性和效率性进行了业绩评价。2004年李彤提出模拟植物生长算法,一种源于植物向光性机理的智能优化算法。目前关于单点设施选址的研究日趋成熟,但是对于单点多因素制约问题由于其本身的复杂性,始终没有得到实质上的突破。在现实问题中设施选址问题往往受到多种因素制约。因此,文中旨在运用植物生长算法,建立韦伯模型,解决多因素制约问题。
韦伯型设施选址问题是运筹学中一个著名问题,特别是对于位置问题进入了深度研究分析。韦伯设施选址涉及定位一套设施并且分配它们的能力来满足一组客户需求,以求总运输成本最小化。在韦伯模型中,工厂、仓库、配送中心都可以构成设施,而超市、零售商可以被视为客户。韦伯模型的数学表达式为

式中,aj(j=1,2,…,m)是第 j个用户的位置,x=(x1,x2,…,xn)是有界闭凸区域,xi为第 i个设施的待定位置,wij是第i个设施到第j个用户的权重,‖xi-aj‖是xi到a的范数距离,本问题采用欧式距离。
1 算法理论
1.1 植物生长模拟算法
植物生长模拟算法(Plant Growth Simulation Algorithm,PGSA)是由李彤提出的,是一种借鉴于植物向光性机理原理的智能优化算法,最初是为了解决整数规划问题。由于PGSA对参数的确定极为简单和宽松,因而被国内外学者大量使用和研究完善。PGSA是由形态素浓度决定的方向性和随机性平衡比较理性的启发式搜索机制,在较短的运算时间内,以较快的计算速度寻找到全局最优解[6-7]。
假设M表示树干的长度,树干上具有T个生长点表示为 SM=(SM1,SM2,…,SMT),每个生长点各自的形态素浓度值表示为 PM=(PM1,PM2,…,PMT);设树枝的单位长度m(m<M)上的r个生长点表示为sm=(sm1,sm2,…,smr),每个生长点各自的形态素浓度值是 pm=(pm1,pm2,…,pmr)。计算树干与树枝上生长点形态素浓度值为
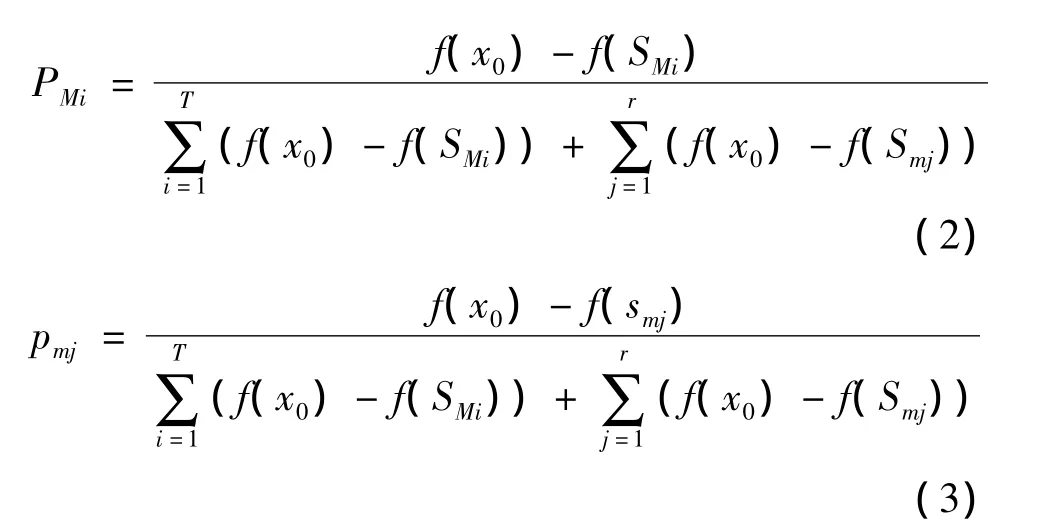
其中,x0表示初始可行解(即树根),f(*)是目标函数值(即生长点的背光函数),f(*)的函数值随着生长点的受光程度的增大而减小,符合生长点形态素浓度值与其各自所受的光照条件及树根光照条件的对应关系。
由式(2),(3)可得
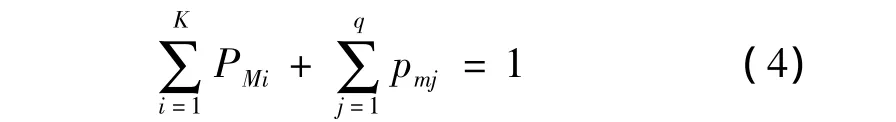
即所有的生长点形态素浓度之和为1。确定了形态素浓度后,浓度值高的生长点优先生长机会大。若树干、枝干上共包含K+q个生长点,即(x1,x2,…,xK+q),由式(2),(3)知每个生长点形态素浓度值为(p1,p2,…,pK+q)。由式(4)可证p1+p2+ … +pK+q=1。接着随机生成一个[0,1]区间的值,用来作为下一个新生长点,循环生长[7-9]。
1.2 PGSA的改进
在传统的PGSA算法求解中,枝干长度根据有界闭箱范围来确定。但是现实中,可行域空间的差异性很大,搜索步长根据具体问题主观设定。当可行域空间较大时,搜索步长的确定较为困难,如果设置不当可能导致无法找到全局最优解。有限元法视整个系统为有限个单元共同连接形成的几何体,划分单元以数字对系统进行描述。为了改进植物生长模拟算法,引入有限元方法自动生成合理的初始网格,建立生长结点的拓扑关系。以此初始生长点结构为基础的模拟计算,使初始点的确定更加简便。如图1所示。谢尔宾斯基地毯的特点是:处处有洞但连续,面积为0但周长无穷大。
将谢尔宾斯基地毯作为约束条件的有界闭箱,以地毯中正方形的4个顶点作为有限元网格的结点,可将有限元网格结点作为模拟植物生长的初始生长点,唯一需要改变的是,在去除掉的部分内部,仍需按照分形原则进行处理并建立初始生长点。采用谢尔宾斯基地毯的结构确定生长点,对于解决可行域空间很大、全局最优解和局部最优解众多的非线性规划问题效果良好。

图1 谢尔宾斯基地毯Fig.1 Sher Pinsky carpet
2 选址影响因素分析及权重的确定
以超市配送中心选址为例,在超市供应链管理中,配送中心的选址是最重要的部分,与库存、配送以及供应网络都有密切关系,故此超市配送中心的选址受到多种因素制约。实际中通常应该考虑以下的影响因素:
1)配送中心的选址要尽可能使配送总距离最短,建立损耗最小的配送网络,减少配送成本和配送时间。
2)配送中心要尽可能靠近人流量多、配送周期短的超市。
3)配送中心要尽可能地少占用土地面积,减少建设成本。为此在选址时要考虑各个超市的货物销售速率,超市的销售情况又与超市覆盖的人口数、人口密度、消费指数等指标相关。
2.1 权重的确定
权重的大小受到众多因素影响,建立一个指标体系分析不同因素影响大小至关重要,指标体系的建立应该遵循以下原则:
1)综合性原则。指标的选择要考虑配送中心制约的各个指标,尽可能地考虑到各个方面的影响因素。
2)代表性原则。所选指标因子必须具有代表性,从众多因子中选择出指标因子应当是能很好地反映超市配送需求的优质因子。
3)实用性原则。建立的指标体系必须是符合我国现阶段国情,各个指标因子也应当是在各类统计数据中较易找到的,且对日后生产和生活能产生积极影响。
4)动态性原则。随着社会和科学技术不断发展和进步,所选取的指标因子数值也应该是动态发展的[10],能够与时俱进,因地制宜,表现出一定的动态性特征,并真实反映影响因素的约束力。
在遵循以上原则基础上,文中结合配送中心的选址影响因素,建立如图2所示的指标体系。
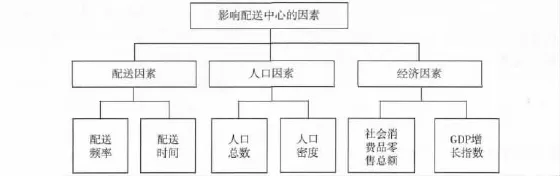
图2 影响配送中心的因素指标体系示意Fig.2 Schematic diagram of the influence factor system of the distribution center
2.1.1 一级指标权重的确定 一级指标层(配送-人口-经济)的权重使用主观赋权G1法[11-12]:
1)专家给予相邻评价指标xk-1和xk重要性程度指标Rk的理性权重赋值;
2)G1法的权重计算公式
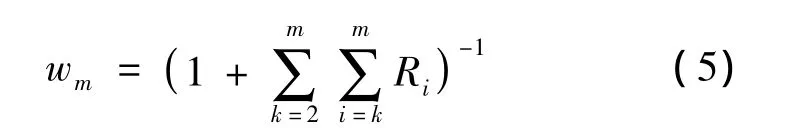
由权重wm可以依次计算得m-1,m-2,3,2个指标权重:wk-1=Rkwk,k=m,m-1,…,3,2。
2.1.2 二级指标权重的确定 二级指标层权重的确定,使用熵值法。
设 xi,j(i=1,2,…,n-1;j=1,2,…,m-1,m)表示第i个系统中第j项指标的观测数据,对于给定的j,xij的差异越大,该指标对系统的比较作用就越大,即可理解为该项指标所传输和包含的信息量越多。熵值法的计算步骤:
1)设ej表示第j个评价指标的熵值,根据熵值计算公式[13]:
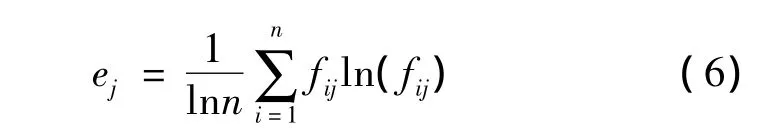
其中,ej> 0,fij=xij/∑xij为第j个指标下第i个系统的特征比重,xij为第i个系统中的第j项指标的观测数据(i=1,2,…,n;j=1,2,…,m)。∑xij为第 j项指标的所有系统观测数据之和;
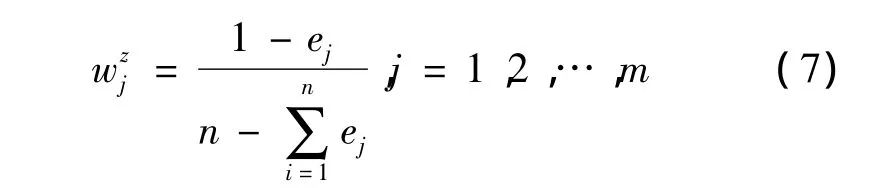
其中,ej为第j个指标的熵值。
熵值法赋权的特点是在所评价的样本中,同一指标之间的数值差别越大,则权重越大。二级指标权重的确定根据不同地区情况而定。
3 坐标转换与改进后PGSA算法步骤
3.1 坐标转换
求解Steiner问题需要使用平面坐标,而在地图上的坐标为地理坐标,通常为WGS-84坐标,所以存在一个坐标转化问题。对于坐标转化问题,文中提供以下两种方式:
1)软件转化法:随着科技的进步,计算机行业的发展,软件的功能越发强大和齐全。对于地理坐标和平面坐标的互换已有多款软件可以完成。COORD就是其中的一款,只需输入对应的地理坐标选择需要转换的坐标即可得到相应的结果,方便准确。
2)公式转化法:软件的本质也是集成了公式化的运算,所以在这里也给出了地理坐标的转化公式。
WGS-84坐标属于地固坐标系,通常采用WGS-84椭球建立,坐标系的原点是地球质心,Z轴指向BIH1984.0定义的协议地球极CTP方向,X轴指向BIH1984.0零度子午面和CTP赤道的交点,Y轴和Z,X轴构成右手坐标[14]。投影变换方式,见公式(5),(6)。
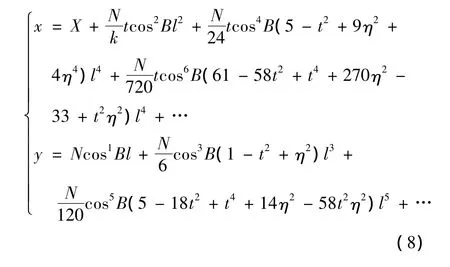

其中,a和b分别表示参考椭球的长短半径;X为赤道至纬度为B的子午线弧长;卯酉圈曲率半径:

上述高斯计算公式,是其泰勒级数的展开式,舍去了6次以上高次项,其子午线弧长计算式舍去8次以上高次项。该式纵横坐标(x,y)的计算精度能够达到0.001 m。
使用转换后得到的平面坐标代入改进的模拟植物生长算法求得全局最优解,再将最优解的平面坐标转换为 WGS-84坐标,以方便工程建设部门使用。
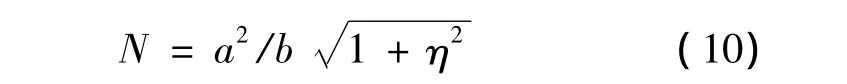
辅助变量:

第二偏心率平方:
3.2 改进后PGSA算法步骤
按照Steiner问题的特点,对人工植物生长的自相似结构做出如下定义:在生长点随机向各个方向生长并产生新枝,新枝之间旋转角度 α为90°,分枝长度一般情况下设定为L/1 000(L为有界闭箱长度)。
w1,w2,…,wn表示n个点的综合权重。求一点p使得minT=∑wi|p-Ai|:
1)确定生长点ai∈X,X为Rn中的有界闭箱,生长点ai为谢尔宾斯基地毯中所有正方形的顶点;
2)求解各生长点的生长概率:
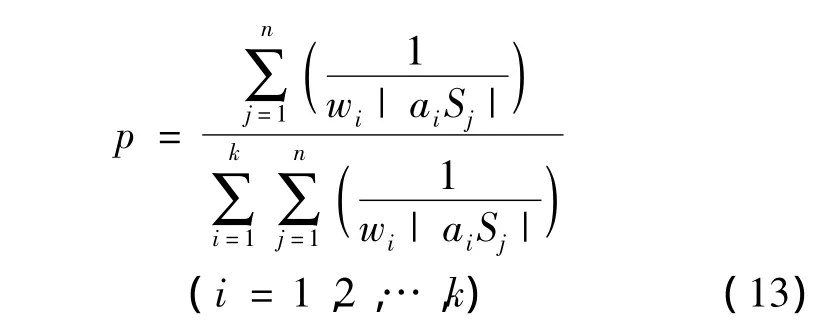
由于目标函数为求最小值,所以计算生长点形态素浓度时取距离之和的倒数(距离之和大的生长点形态素浓度较小);
3)根据2)计算结果建立各生长点在0~1之间的概率空间,以随机数选择本次迭代生长点;
4)确定步长(一般为L/1 000,L为有界闭箱);
5)若达到设定的迭代次数后不再产生新的生长点,且得到全局最优解和局部最优解,则停止迭代,否则转回2)。
4 实证
以无锡市家乐福超市配送中心的选址问题为研究背景。无锡市的家乐福超市共有7家,分布在滨湖、新区、南长、北塘、崇安、锡山6个区。现要考虑设置一个物资配送中心,该点应满足:
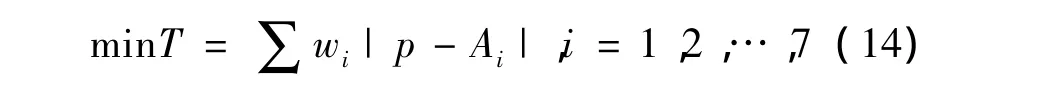
结合无锡市各区的经济状况、配送因素、人口因素(一级指标)以及配送频率、配送时间、人口总数、人口密度、消费指数、GDP增长指数(二级指标)。运用熵值法可以得到指标体系中二级指标的赋权,再结合一级指标赋权,可以得到各指标的最终权重,进而得到各个超市分店的最终权重如表1所示。
通过查询百度地图,得到各个区家乐福具体的WGS-84坐标(即经纬度,中央经线设定为120°),利用坐标转换公式(5),(6)将其变换为平面坐标,如表1所示。
将平面坐标数据带入模拟植物生长算法的程序中,利用Matlab软件经过5 000步迭代,耗时8 s左右得到全局最优解如表1所示。
图3所示为百度地图中各家乐福及配送中具体位置。
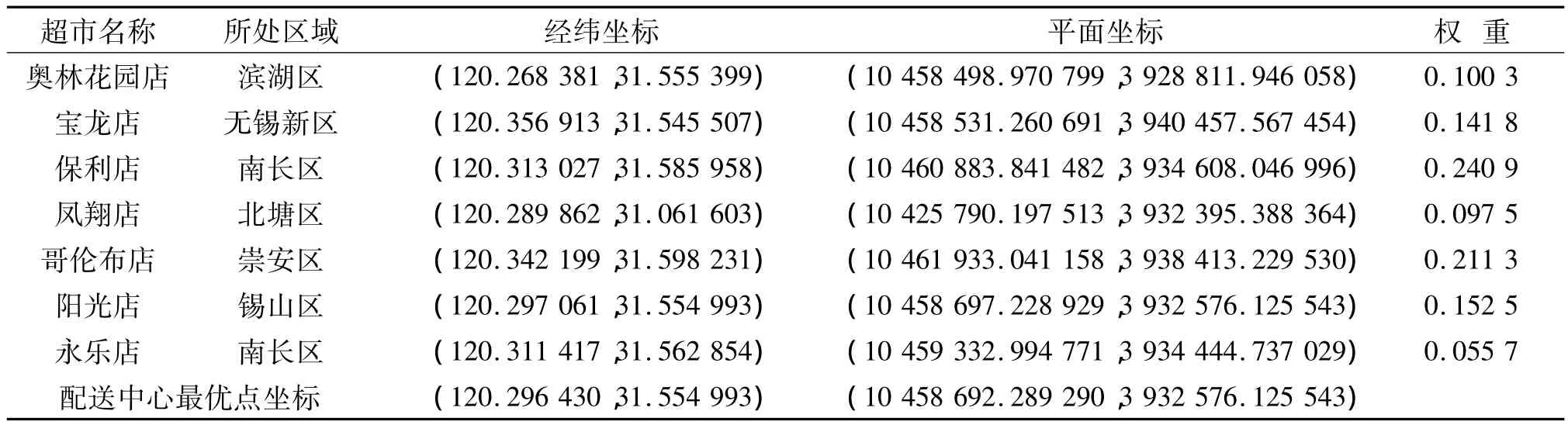
表1 超市坐标和权重Tab.1 Coordinates and weights of the supermarket
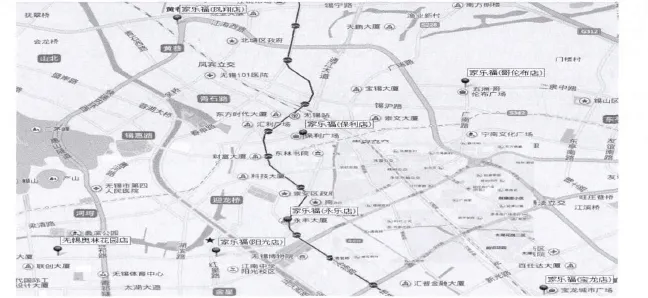
图3 百度地图中各家乐福及配送中心具体位置示意Fig.3 Specific location of the Carrefour and distribution center schematic in Baidu map
5 结语
在实际设施选址问题中,会受到多因素的影响和制约。多因素权重合成处理直接影响到最终选址的结果。文中从二级指标体系出发,通过G1法和熵值法确定客户的权重。
根据PGSA算法的植物向光性概率生长动力机制为启发式准则,具有较强的全局搜索能力、计算精度高、稳定性好以及应用性强的特点,通过程序计算,得到全局最优解。最后,以无锡市家乐福超市配送中心的选址问题为研究背景进行了实证。
[1]Ali Jamalian,Maziar Salahi.Robust solutions to multi-facility Weber location problem under interval and ellipsoidal uncertainty[J].Applied Mathematics and Computation,2014(242):179-186.
[2]李磊,谢小璐.韦伯型多点设施优化选址的组合算法研究[J].计算机工程与应用,2013,49(22):258-261.
LI Lei,XIE Xiaolu.Study on the combination algorithm of location optimization of Webb type multipoint facilities[J].Computer Engineering and Application,2013,49(22):258-261.(in Chinese)
[3]Harry Venables,Alfredo Moscardini.Ant Colony Optimization and Swarm Intelligence[M].Brussels,Belgium:Springer,2006.
[4]Lyamine Bouhafs,Amir Hajjam,Abder Koukam.Knowledge based and Intelligent Information and Engineering Systems[M].Santiago,Chile:Springerlink,2009.
[5]李彤,王春峰,王文波,等.求解整数规划的一种仿生类全局优化算法—模拟植物生长算法[J].系统工程理论与实践,2005,25(1):76-85.
LI Tong,WANG Chunfeng,WANG Wenbo,et al.A global optimization bionics algorithm for solving integer programming-the plant growth simulation algorithm[J].Systems Engineering Theory and Practice,2005,25(1):76-85.(in Chinese)
[6]李彤,王众托.模拟植物生长算法在设施选址问题中的应用[J].系统工程理论与实践,2008,28(12):107-115.
LI Tong,WANG Zongtuo.Plant growth simulation algorithm of location and its application in facilities[J].Systems Engineering Theory and Practice,2008,28(12):107-115.(in Chinese)
[7]李彤,陈畴镛,宿伟玲.求解二层规划问题的模拟植物生长算法[J].运筹与管理,2010,10(5):123-128.
LI Tong,CHEN Chóuyong,SU Weiling.Plant simulation for solving two programming problems growth algorithm[J].Operations Research and Management,2010,10(5):123-128.(in Chinese)
[8]刘学.农村集中供水管理模式与运营问题研究[D].无锡:江南大学,2012.
[9]迟国泰,祝志川,张玉玲.基于熵权—G1法的科技评价模型及实证研究[J].科学学研究,2008,26(6):1210-1220.
CHI Guotai,ZHU Zhichuang,ZHANG Yuling.Model of technology evaluation based on entropy weight G1method and empirical study based on[J].Studies in Science of Science,2008,26(6):1210-1220.(in Chinese)
[10]符林.基于科学发展观的经济评价研究及应用[D].大连:大连理工大学,2008.
[11]郭亚军.综合评价理论与方法[M].北京:科学出版社,2002.
[12]肖翰珅.关于广义Fermat点唯一性的探讨[J].数学通报,2012,51(10):44-47.
XIAO Hankun.Discussion on the uniqueness of generalized Fermat points[J].Mathematical Bulletin,2012,51(10):44-47.(in Chinese)
[13]罗德安,廖丽琼.一种车载GPS系统坐标转换公式及其应用[J].西南交通大学学报,2001,36(4):365-368.
LUO Dean,LIAO Liqion.A vehicular GPS coordinate transform formula and its application[J].Journal of Southwest Jiaotong University,2001,36(4):365-368.(in Chinese)
[14]Mahmood Neshati,Hamid Beigy,Djoerd Hiemstra.Expert group formation using facility location analysis[J].Information Processing and Management,2014(50):361-383.
--先进无机材料论坛例记(Ⅱ)
--先进无机材料论坛例记(Ⅰ)

